14.4: Uso de la simulación de Montecarlo

Última actualización
Guardar como PDF

Page ID: 150563

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Volvamos a nuestro ejemplo de los tiempos de finalización de exámenes. Digamos que administro tres cuestionarios y registro los tiempos de finalización de cada alumno para cada examen, lo que podría parecerse a las distribuciones que se presentan en la Figura 14.2.

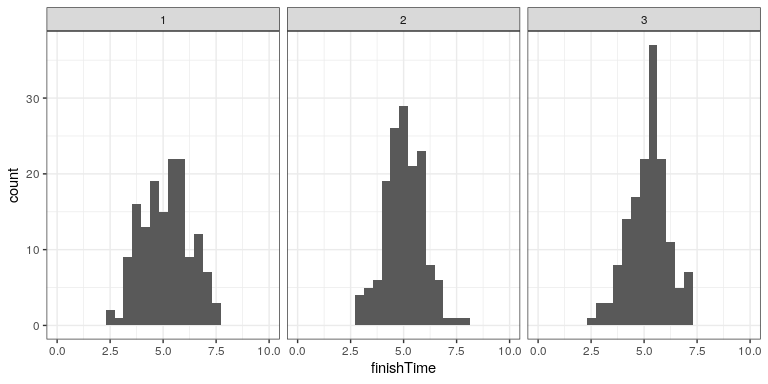
Figura 14.2: Distribuciones simuladas de tiempo de acabado.

Sin embargo, lo que realmente queremos saber no es cómo se ve la distribución de los tiempos de finalización, sino cómo es la distribución del tiempo de finalización más largo para cada cuestionario. Para ello, podemos simular el tiempo de finalización de un cuestionario, utilizando la suposición de que los tiempos de finalización se distribuyen normalmente, como se indicó anteriormente; para cada uno de estos cuestionarios simulados, luego registramos el tiempo de finalización más largo. Repetimos esta simulación un gran número de veces (5000 deberían ser suficientes) y registramos la distribución de los tiempos de finalización, que se muestra en la Figura 14.3.

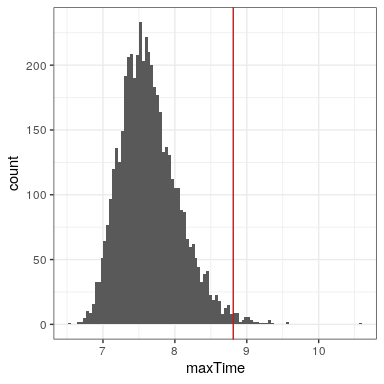
Figura 14.3: Distribución de los tiempos máximos de acabado entre simulaciones.

Esto demuestra que el percentil 99 de la distribución del tiempo de finalización cae en 8.81, es decir, que si tuviéramos que dar tanto tiempo para el cuestionario, entonces todos deberían terminar el 99% del tiempo. Siempre es importante recordar que nuestras suposiciones importan —si están equivocadas, entonces los resultados de la simulación son inútiles. En este caso, asumimos que la distribución del tiempo de finalización se distribuía normalmente con una media y desviación estándar particulares; si estos supuestos son incorrectos (y casi con certeza lo son), entonces la respuesta verdadera podría ser muy diferente.