16.4: NHST en un contexto moderno - Pruebas múltiples

Última actualización
Guardar como PDF

Page ID: 150474

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hasta ahora hemos discutido ejemplos en los que estamos interesados en probar una única hipótesis estadística, y esto es consistente con la ciencia tradicional que a menudo mide solo unas pocas variables a la vez. Sin embargo, en la ciencia moderna muchas veces podemos medir millones de variables por individuo. Por ejemplo, en estudios genéticos que cuantifican todo el genoma, puede haber muchos millones de medidas por individuo, y en las imágenes cerebrales a menudo recolectamos datos de más de 100,000 ubicaciones en el cerebro a la vez. Cuando se aplican pruebas de hipótesis estándar en estos contextos, pueden suceder cosas malas a menos que tengamos el cuidado adecuado.

Veamos un ejemplo para ver cómo podría funcionar esto. Existe un gran interés en comprender los factores genéticos que pueden predisponer a los individuos a enfermedades mentales mayores como la esquizofrenia, porque sabemos que alrededor del 80% de la variación entre individuos en presencia de esquizofrenia se debe a diferencias genéticas. El Proyecto Genoma Humano y la consiguiente revolución en la ciencia del genoma han proporcionado herramientas para examinar las muchas formas en que los humanos difieren entre sí en sus genomas. Un enfoque que se ha utilizado en los últimos años se conoce como un estudio de asociación de todo el genoma (GWAS), en el que el genoma de cada individuo se caracteriza en un millón o más lugares de su genoma para determinar qué letras del código genético (que llamamos “variantes”) tienen en ese ubicación. Después de que estos hayan sido determinados, los investigadores realizan una prueba estadística en cada ubicación del genoma para determinar si las personas diagnosticadas con esquizoprenia tienen más o menos probabilidades de tener una variante específica en esa ubicación.

Imaginemos qué pasaría si los investigadores simplemente preguntaran si la prueba era significativa a p<.05 en cada ubicación, cuando de hecho no hay un efecto verdadero en ninguna de las ubicaciones. Para ello, generamos un gran número de valores t simulados a partir de una distribución nula, y preguntamos cuántos de ellos son significativos en p<.05. Hagamos esto muchas veces, y cada vez cuente hasta cuántas de las pruebas salen como significativas (ver Figura 16.8).

## [1] "corrected familywise error rate: 0.036"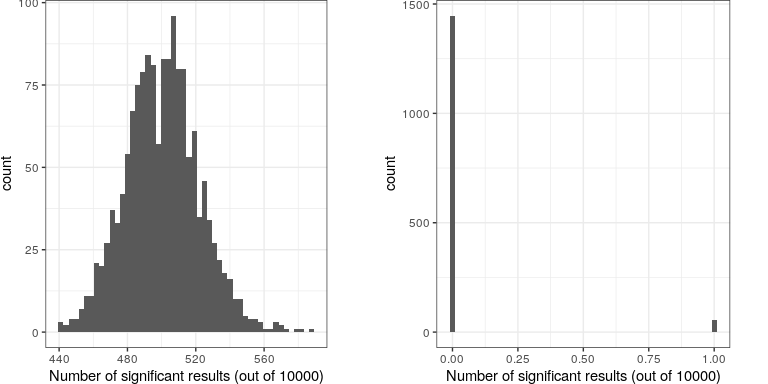

Figura 16.8: Izquierda: Histograma del número de resultados significativos en cada conjunto de 1 millón de pruebas estadísticas, cuando de hecho no hay ningún efecto verdadero. Derecha: Histograma del número de resultados significativos en todas las ejecuciones de simulación después de aplicar la corrección de Bonferroni para múltiples pruebas.

Esto demuestra que alrededor del 5% de todas las pruebas fueron significativas en cada ejecución, lo que significa que si usáramos p < .05 como nuestro umbral de significancia estadística, entonces incluso si no hubiera relaciones verdaderamente significativas presentes, todavía “encontraríamos” alrededor de 500 genes que aparentemente eran significativos (el número esperado de resultados significativos es simplemente $n *\ alfa$ ). Eso es porque mientras controlamos el error por prueba, no controlamos el error familiar, o el error en todas las pruebas, que es lo que realmente queremos controlar si vamos a estar viendo los resultados de una gran cantidad de pruebas. Usando p<.05, nuestra tasa de error familiar en el ejemplo anterior es una, es decir, estamos prácticamente garantizados de cometer al menos un error en cualquier estudio en particular.

Una forma sencilla de controlar el error familiar es dividir el nivel alfa por el número de pruebas; esto se conoce como la corrección de Bonferroni, que lleva el nombre del estadístico italiano Carlo Bonferroni. Usando los datos de nuestro ejemplo anterior, vemos en Figura?? que sólo alrededor del 5 por ciento de los estudios muestran algún resultado significativo utilizando el nivel alfa corregido de 0.000005 en lugar del nivel nominal de .05. Hemos controlado efectivamente el error familiar, de tal manera que la probabilidad de cometer algún error en nuestro estudio se controla justo alrededor de .05.