16.3: El Proceso de Prueba de Hipótesis Nulas

Última actualización
Guardar como PDF

Page ID: 150467

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Podemos romper el proceso de pruebas de hipótesis nulas en una serie de pasos:

Formular una hipótesis que encarne nuestra predicción (antes de ver los datos)
Recopilar algunos datos relevantes para la hipótesis
Especificar hipótesis nulas y alternativas
Ajustar un modelo a los datos que representan la hipótesis alternativa y calcular un estadístico de prueba
Calcular la probabilidad del valor observado de esa estadística asumiendo que la hipótesis nula es verdadera
Evaluar la “significancia estadística” del resultado

Para un ejemplo práctico, usemos los datos de NHANES para hacer la siguiente pregunta: ¿La actividad física está relacionada con el índice de masa corporal? En el conjunto de datos de NHANES, se preguntó a los participantes si participan regularmente en deportes, fitness o actividades recreativas de intensidad moderada o vigorosa (almacenados en la variable $PhysActive$ ). Los investigadores también midieron la estatura y el peso y los utilizaron para calcular el Índice de Masa Corporal (IMC):

$IMC =\ frac {peso (kg)} {altura (m) ^2}$

16.3.1 Paso 1: Formular una hipótesis de interés

Para el paso 1, planteamos la hipótesis de que el IMC es mayor para las personas que no realizan actividad física, en comparación con las que lo hacen.

16.3.2 Paso 2: Recopilar algunos datos

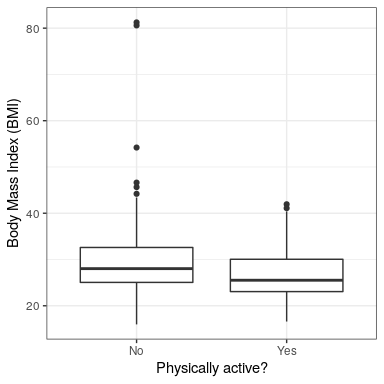
Para el paso 2, recopilamos algunos datos. En este caso, tomaremos muestras de 250 individuos del conjunto de datos NHANES. La Figura 16.1 muestra un ejemplo de dicha muestra, mostrándose el IMC por separado para individuos activos e inactivos.

Cuadro 16.1: Resumen de datos de IMC para individuos activos versus inactivos
PhysActive	N	media	sd
No	131	30	9.0
Sí	119	27	5.2

Gráfica de caja de datos de IMC de una muestra de adultos del conjunto de datos NHANES, dividido por si reportaron haber realizado actividad física regular. — Figura 16.1: Gráfica de caja de datos de IMC de una muestra de adultos del conjunto de datos NHANES, dividido por si reportaron realizar actividad física regular.

16.3.3 Paso 3: Especificar las hipótesis nulas y alternativas

Para el paso 3, necesitamos especificar nuestra hipótesis nula (a la que llamamos $H$ ) y nuestra hipótesis alternativa (a la que llamamos $H_A$ ). $H$ es la línea de base contra la que probamos nuestra hipótesis de interés: es decir, ¿cómo esperaríamos que fueran los datos si no hubiera efecto? La hipótesis nula siempre implica algún tipo de igualdad (=, $\ le$ , o $\ ge$ ). $H_A$ describe lo que esperamos si realmente hay un efecto. La hipótesis alternativa siempre implica algún tipo de desigualdad ( $\ ne$ , > o <). Es importante destacar que la prueba de hipótesis nula opera bajo el supuesto de que la hipótesis nula es verdadera a menos que la evidencia demuestre lo contrario.

También tenemos que decidir si usar hipótesis direccionales o no direccionales. Una hipótesis no direccional simplemente predice que habrá una diferencia, sin predecir en qué dirección irá. Para el ejemplo de IMC/actividad, una hipótesis nula no direccional sería:

$H0$

y la hipótesis alternativa no direccional correspondiente sería:

$HA: BMI_ {activo}\ neq BMI_ {inactivo}$

Una hipótesis direccional, en cambio, predice en qué dirección iría la diferencia. Por ejemplo, tenemos fuertes conocimientos previos para predecir que las personas que realizan actividad física deben pesar menos que las que no, por lo que propondríamos la siguiente hipótesis nula direccional:

$H0: BMI_ {activo}\ ge BMI_ {inactivo}$

y alternativa direccional:

$JA$

Como veremos más adelante, probar una hipótesis no direccional es más conservador, por lo que generalmente se prefiere esto a menos que exista una fuerte razón a priori para plantear la hipótesis de un efecto en una dirección particular. ¡Cualquier hipótesis de dirección debe especificarse antes de mirar los datos!

16.3.4 Paso 4: Ajustar un modelo a los datos y calcular un estadístico de prueba

Para el paso 4, queremos usar los datos para calcular una estadística que finalmente nos permita decidir si la hipótesis nula es rechazada o no. Para ello, el modelo necesita cuantificar la cantidad de evidencia a favor de la hipótesis alternativa, relativa a la variabilidad en los datos. Así podemos pensar en el estadístico de prueba como una medida del tamaño del efecto en comparación con la variabilidad en los datos. En general, este estadístico de prueba tendrá una distribución de probabilidad asociada a él, ya que eso nos permite determinar qué tan probable es nuestro valor observado del estadístico bajo la hipótesis nula.

Para el ejemplo de IMC, necesitamos un estadístico de prueba que nos permita probar una diferencia entre dos medias, ya que las hipótesis se establecen en términos de IMC medio para cada grupo. Una estadística que a menudo se usa para comparar dos medias es la estadística t, desarrollada por primera vez por el estadístico William Sealy Gossett, quien trabajó para la Cervecería Guiness en Dublín y escribió bajo el seudónimo “Student”, de ahí que a menudo se le llama “estadística t de Student”. El estadístico t es apropiado para comparar las medias de dos grupos cuando los tamaños de muestra son relativamente pequeños y se desconoce la desviación estándar poblacional. El estadístico t para la comparación de dos grupos independientes se calcula como:

$t =\ frac {\ bar {X_1} -\ bar {X_2}} {\ sqrt {\ frac {S_1^2} {n_1} +\ frac {S_2^2} {n_2}}}$

donde $\ bar {X} _1$ y $\ bar {X} _2$ son los medios de los dos grupos, $S$ y $S$ son las varianzas estimadas de los grupos, y $n$ y $n$ son los tamaños de los dos grupos. Obsérvese que el denominador es básicamente un promedio del error estándar de la media para las dos muestras. Así, se puede ver el estadístico t como una forma de cuantificar cuán grande es la diferencia entre grupos en relación con la variabilidad muestral de las medias que se están comparando.

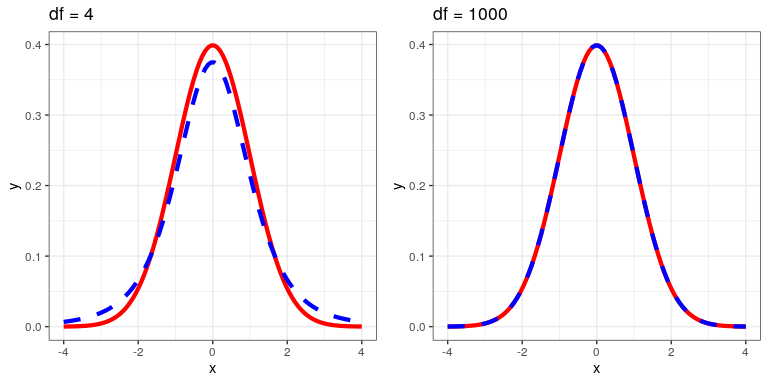
El estadístico t se distribuye de acuerdo con una distribución de probabilidad conocida como distribución t. La distribución t se parece bastante a una distribución normal, pero difiere dependiendo del número de grados de libertad, que para este ejemplo es el número de observaciones menos 2, ya que hemos calculado dos medias y así renunciado a dos grados de libertad. Cuando los grados de libertad son grandes (digamos 1000), entonces la distribución t se parece esencialmente a la distribución normal, pero cuando son pequeños entonces la distribución t tiene colas más largas que la normal (ver Figura 16.2).

Figura 16.2: Cada panel muestra la distribución t (en línea discontinua azul) superpuesta sobre la distribución normal (en línea roja continua). El panel izquierdo muestra una distribución t con 4 grados de libertad, en cuyo caso la distribución es similar pero tiene colas ligeramente más anchas. El panel derecho muestra una distribución t con 1000 grados de libertad, en cuyo caso es prácticamente idéntica a la normal.

16.3.5 Paso 5: Determinar la probabilidad de los datos bajo la hipótesis nula

Este es el paso en el que NHST comienza a violar nuestra intuición —en lugar de determinar la probabilidad de que la hipótesis nula sea verdadera dados los datos, en cambio determinamos la probabilidad de los datos bajo la hipótesis nula- ¡porque comenzamos asumiendo que la hipótesis nula es verdadera! Para ello, necesitamos conocer la distribución de probabilidad para el estadístico bajo la hipótesis nula, de manera que podamos preguntar qué tan probables son los datos bajo esa distribución. Antes de pasar a nuestros datos de IMC, comencemos con algunos ejemplos más simples.

16.3.5.1 Aleatorización: Un ejemplo muy sencillo

Digamos que deseamos determinar si una moneda es justa. Para recopilar datos, volteamos la moneda 100 veces, y contamos 70 cabezas. En este ejemplo, $H_0: P (cabezas) =0.5$ y $H_A: P (cabezas)\ neq 0.5$ , y nuestra estadística de prueba es simplemente el número de cabezas que contamos. La pregunta que entonces queremos hacernos es: ¿Qué tan probable es que observemos 70 cabezas si la verdadera probabilidad de cabezas es de 0.5. Podemos imaginar que esto podría suceder muy ocasionalmente solo por casualidad, pero no parece muy probable. Para cuantificar esta probabilidad, podemos usar la distribución binomial:

$P (X < k) =\ suma_ {i=0} ^k\ binom {N} {k} p^i (1-p) ^ {(n-i)}$ Esta ecuación nos dirá la probabilidad de un cierto número de cabezas o menos, dada una probabilidad particular de cabezas. Sin embargo, lo que realmente queremos saber es la probabilidad de un cierto número o más, que podemos obtener restando de uno, en base a las reglas de probabilidad:

$P (X\ ge k) = 1 - P (X < k)$

Distribución del número de cabezas (de 100 volteretas) a través de 100,000 runsl simuladas con el valor observado de 70 volteretas representado por la línea vertical. — Figura 16.3: Distribución del número de cabezas (de 100 volteos) a través de 100,000 runsl simuladas con el valor observado de 70 volteretas representado por la línea vertical.

Podemos calcular la probabilidad para nuestro ejemplo usando la función pbinom (). La probabilidad de 69 o menos cabezas dadas P (cabezas) =0.5 es 0.999961, por lo que la probabilidad de 70 o más cabezas es simplemente una menos ese valor (0.000039) Este cálculo nos muestra que la probabilidad de obtener 70 cabezas si la moneda es efectivamente justa es muy pequeña.

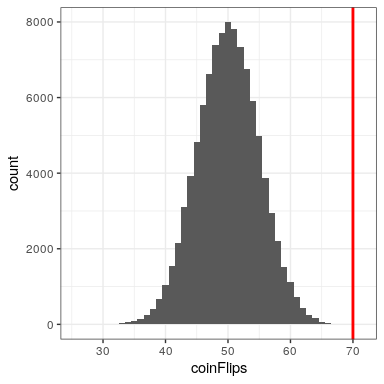
Ahora bien, ¿y si no tuviéramos la función pbinom () para decirnos la probabilidad de ese número de cabezas? En cambio, podríamos determinarlo mediante simulación: volteamos repetidamente una moneda 100 veces usando una probabilidad real de 0.5, y luego calculamos la distribución del número de cabezas a través de esas ejecuciones de simulación. La Figura 16.3 muestra el resultado de esta simulación. Aquí podemos ver que la probabilidad calculada vía simulación (0.000030) es muy cercana a la probabilidad teórica (.00004).

Hagamos el cómputo análogo para nuestro ejemplo de IMC. Primero calculamos el estadístico t utilizando los valores de nuestra muestra que calculamos anteriormente, donde encontramos eso (t = 3.86). La pregunta que entonces queremos hacernos es: ¿Cuál es la probabilidad de que encontremos un estadístico t de este tamaño, si la verdadera diferencia entre grupos es cero o menor (es decir, la hipótesis nula direccional)?

Podemos usar la distribución t para determinar esta probabilidad. Nuestro tamaño muestral es de 250, por lo que la distribución t apropiada tiene 248 grados de libertad porque perdemos uno por cada una de las dos medias que calculamos. Podemos usar la función pt () en R para determinar la probabilidad de encontrar un valor del estadístico t mayor o igual que nuestro valor observado. Tenga en cuenta que queremos saber la probabilidad de un valor mayor que nuestro valor observado, pero por defecto pt () nos da la probabilidad de un valor menor que el que le proporcionamos, así que tenemos que decirle explícitamente para proporcionarnos la probabilidad de “cola superior” (estableciendo lower.tail = FALSO). Encontramos eso (p (t > 3.86, df = 248) = 0.000), lo que nos dice que nuestro valor estadístico t observado de 3.86 es relativamente improbable si la hipótesis nula es realmente cierta.

En este caso, utilizamos una hipótesis direccional, por lo que solo tuvimos que mirar un extremo de la distribución nula. Si quisiéramos probar una hipótesis no direccional, entonces tendríamos que ser capaces de identificar cuán inesperado es el tamaño del efecto, independientemente de su dirección. En el contexto de la prueba t, esto significa que necesitamos saber qué tan probable es que la estadística sea tan extrema ya sea en la dirección positiva o negativa. Para ello, multiplicamos el valor t observado por -1, ya que la distribución t se centra alrededor de cero, y luego sumamos las dos probabilidades de cola para obtener un valor p de dos colas: (p (t > 3.86 o t< -3.86, df = 248) = 0.000). Aquí vemos que el valor p para la prueba de dos colas es dos veces más grande que el de la prueba de una cola, lo que refleja el hecho de que un valor extremo es menos sorprendente ya que podría haber ocurrido en cualquier dirección.

¿Cómo eliges si se usa una prueba de una cola versus una de dos colas? La prueba de dos colas siempre va a ser más conservadora, así que siempre es una buena apuesta usar esa, a menos que tuvieras una razón previa muy fuerte para usar una prueba de una cola. En ese caso, deberías haber escrito la hipótesis antes de mirar los datos. En el Capítulo 32 discutiremos la idea de pre-registro de hipótesis, que formaliza la idea de anotar tus hipótesis antes de que veas los datos reales. Nunca debes tomar una decisión sobre cómo realizar una prueba de hipótesis una vez que hayas mirado los datos, ya que esto puede introducir un sesgo serio en los resultados.

16.3.5.2 Cálculo de los valores p mediante aleatorización

Hasta ahora hemos visto cómo podemos usar la distribución t para calcular la probabilidad de los datos bajo la hipótesis nula, pero también podemos hacerlo usando simulación. La idea básica es que generemos datos simulados como los que esperaríamos bajo la hipótesis nula, para luego preguntar qué tan extremos son los datos observados en comparación con esos datos simulados. La pregunta clave es: ¿Cómo podemos generar datos para los que la hipótesis nula es verdadera? La respuesta general es que podemos reorganizar aleatoriamente los datos de una manera particular que haga que los datos se vean como lo harían si el nulo fuera realmente cierto. Esto es similar a la idea de bootstrapping, en el sentido de que utiliza nuestros propios datos para llegar a una respuesta, pero lo hace de una manera diferente.

16.3.5.3 Aleatorización: un ejemplo sencillo

Empecemos con un ejemplo sencillo. Digamos que queremos comparar la capacidad media en cuclillas de los futbolistas con los corredores de campo traviesa, con $H_0:\ mu_ {FB}\ le\ mu_ {XC}$ y $H$ . Medimos la capacidad máxima en cuclillas de 5 futbolistas y 5 corredores de campo traviesa (que generaremos aleatoriamente, asumiendo que $\ mu_ {FB} = 300$ , $\ mu_ {XC} = 140$ , y $\ sigma = 30$ ).

Cuadro 16.2: Datos de sentadillas para los dos grupos
grupo	en cuclillas
FB	335
FB	350
FB	230
FB	290
FB	325
XC	115
XC	115
XC	170
XC	175
XC	215

Tabla 16.2: Datos en cuclillas después de aleatorizar etiquetas de grupo
en cuclillas	ScrambledGroup
335	FB
350	FB
230	XC
290	FB
325	FB
115	XC
115	XC
170	FB
175	XC
215	XC

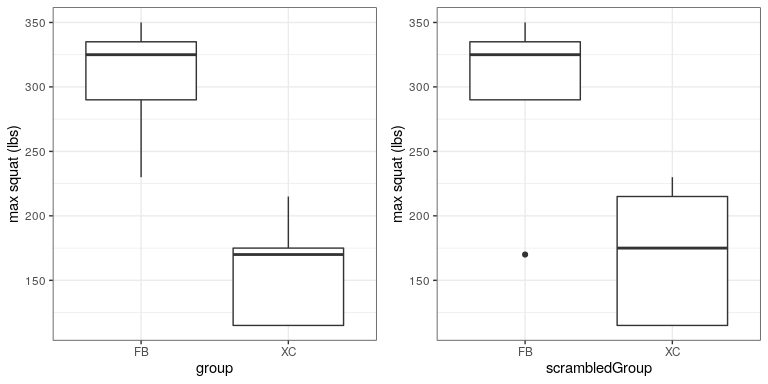
Izquierda: Tramas de caja de habilidad simulada en cuclillas para jugadores de fútbol y corredores de cross-country. Derecha: Parcelas de caja para sujetos asignados a cada grupo después de revolver etiquetas de grupo. — Figura 16.4: Izquierda: Gráficas de caja de habilidad simulada para jugadores de fútbol y corredores de cross-country. Derecha: Parcelas de caja para sujetos asignados a cada grupo después de etiquetas de grupos revueltos.

A partir de la gráfica de la Figura 16.4 queda claro que existe una gran diferencia entre los dos grupos. Podemos hacer una prueba t estándar para probar nuestra hipótesis, usando el comando t.test () en R, que da el siguiente resultado:

## 
##  Two Sample t-test
## 
## data:  squat by group
## t = 5, df = 8, p-value = 4e-04
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##   95 Inf
## sample estimates:
## mean in group FB mean in group XC 
##              306              158

Si miramos el valor p reportado aquí, vemos que la probabilidad de tal diferencia bajo la hipótesis nula es muy pequeña, usando la distribución t para definir el nulo.

Ahora veamos cómo podríamos responder a la misma pregunta usando la aleatorización. La idea básica es que si la hipótesis nula de no diferencia entre grupos es cierta, entonces no debería importar de qué grupo provenga uno (futbolistas versus corredores de cross country) — así, para crear datos que sean como nuestros datos reales pero que también se ajusten a la hipótesis nula, podemos reordenar aleatoriamente el grupo etiquetas para los individuos en el conjunto de datos, y luego recalcular la diferencia entre los grupos. Los resultados de tal barajado se muestran en la Figura?? .

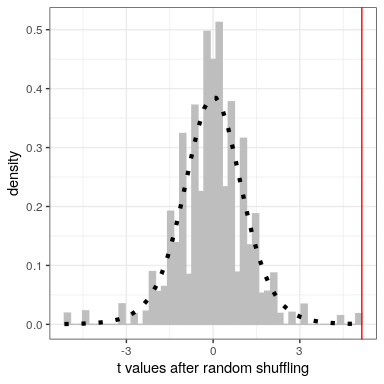
Figura 16.5: Histograma de valores t para la diferencia de medias entre los grupos de fútbol y cross-country después de barajar aleatoriamente la pertenencia al grupo. La línea vertical denota la diferencia real observada entre los dos grupos, y la línea punteada muestra la distribución t teórica para este análisis.

Después de revolver las etiquetas, vemos que los dos grupos son ahora mucho más similares, y de hecho el grupo cross-country ahora tiene una media ligeramente superior. Ahora hagamos eso 10000 veces y almacenemos la estadística t para cada iteración; esto puede tardar un momento en completarse. La Figura 16.5 muestra el histograma de los valores t en todos los barajados aleatorios. Como se esperaba bajo la hipótesis nula, esta distribución se centra en cero (la media de la distribución es -0.016. De la figura también podemos ver que la distribución de t valores después del barajado sigue aproximadamente la distribución t teórica bajo la hipótesis nula (con media=0), mostrando que la aleatorización funcionó para generar datos nulos. Podemos calcular el valor p a partir de los datos aleatorios midiendo cuántos de los valores barajados son al menos tan extremos como el valor observado: p (t > 5.14, df = 8) usando aleatorización = 0.00380. Este valor p es muy similar al valor p que obtuvimos usando la distribución t, y ambos son bastante extremos, lo que sugiere que es muy poco probable que los datos observados hayan surgido si la hipótesis nula es cierta -y en este caso sabemos que no es cierto, porque generamos los datos.

16.3.5.3.1 Aleatorización: IMC/Ejemplo de actividad

Ahora usemos la aleatorización para calcular el valor p para el ejemplo de BMI/actividad. En este caso, barajaremos aleatoriamente la variable PhysActive y calcularemos la diferencia entre grupos después de cada mezcla, y luego compararemos nuestro estadístico t observado con la distribución de t estadísticas de los conjuntos de datos barajados. La Figura 16.6 muestra la distribución de los valores t de las muestras barajadas, y también podemos calcular la probabilidad de encontrar un valor tan grande o mayor que el valor observado. El valor p obtenido de la aleatorización (0.0000) es muy similar al obtenido usando la distribución t (0.0001). La ventaja de la prueba de aleatorización es que no requiere que supongamos que los datos de cada uno de los grupos se distribuyen normalmente, aunque la prueba t es generalmente bastante robusta ante violaciones de esa suposición. Además, la prueba de aleatorización puede permitirnos calcular valores p para estadísticas cuando no tenemos una distribución teórica como la que hacemos para la prueba t.

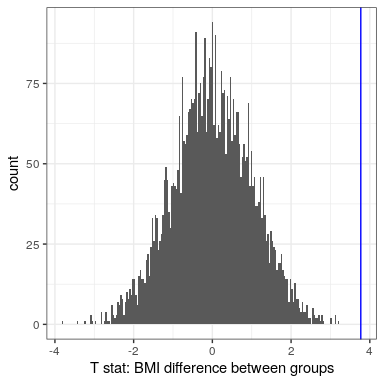
Histograma de t estadística después de barajar etiquetas de grupo, con el valor observado del estadístico t mostrado en la línea vertical, y valores al menos tan extremos como el valor observado mostrado en gris más claro — Figura 16.6: Histograma de la estadística t después de barajar etiquetas de grupo, con el valor observado del estadístico t mostrado en la línea vertical, y valores al menos tan extremos como el valor observado mostrado en gris más claro

Tenemos que hacer una suposición principal cuando utilizamos la prueba de aleatorización, a la que nos referimos como intercambiabilidad. Esto significa que todas las observaciones se distribuyen de la misma manera, de tal manera que podemos intercambiarlas sin cambiar la distribución general. El lugar principal donde esto puede descomponerse es cuando hay observaciones relacionadas en los datos; por ejemplo, si tuviéramos datos de individuos en 4 familias diferentes, entonces no podríamos asumir que los individuos eran intercambiables, porque los hermanos estarían más cerca entre sí que de individuos de otros familias. En general, si los datos se obtuvieron por muestreo aleatorio, entonces se debería mantener el supuesto de intercambiabilidad.

16.3.6 Paso 6: Evaluar la “significancia estadística” del resultado

El siguiente paso es determinar si el valor p que resulta del paso anterior es lo suficientemente pequeño como para que estemos dispuestos a rechazar la hipótesis nula y concluir en su lugar que la alternativa es verdadera. ¿Cuanta evidencia requerimos? Esta es una de las preguntas más polémicas en la estadística, en parte porque requiere de un juicio subjetivo —no hay una respuesta “correcta”.

Históricamente, la respuesta más común a esta pregunta ha sido que debemos rechazar la hipótesis nula si el valor p es menor que 0.05. Esto proviene de los escritos de Ronald Fisher, quien ha sido referido como “la figura más importante en las estadísticas del siglo XX” (Efron 1998):

“Si P está entre .1 y .9 ciertamente no hay razón para sospechar la hipótesis probada. Si está por debajo del .02 se indica fuertemente que la hipótesis no da cuenta de la totalidad de los hechos. A menudo no nos desviaremos si trazamos una línea convencional al .05... es conveniente trazar la línea aproximadamente al nivel en el que podemos decir: O hay algo en el tratamiento, o ha ocurrido una coincidencia como que no ocurre más de una vez en veinte ensayos” (Fisher 1925)

Sin embargo, Fisher nunca tuvo la intención de $p < 0.05$ para ser una regla fija:

“ningún trabajador científico tiene un nivel fijo de significación en el que de año en año, y en todas las circunstancias, rechaza hipótesis; más bien da su mente a cada caso particular a la luz de sus pruebas y sus ideas” [pec:1956]

En cambio, es probable que se convirtiera en un ritual debido a la dependencia de tablas de valores p que se utilizaron antes de la computación, lo que facilitó el cálculo de valores p para valores arbitrarios de una estadística. Todas las tablas tenían una entrada para 0.05, lo que facilita determinar si la estadística excedía el valor necesario para alcanzar ese nivel de significancia.

La elección de los umbrales estadísticos sigue siendo profundamente controvertida, y recientemente (Benjamin et al., 2018) se ha propuesto cambiar el umbral estándar de .05 a .005, haciendo que sea sustancialmente más estricto y por lo tanto más difícil rechazar la hipótesis nula. En gran parte este movimiento se debe a la creciente preocupación de que la evidencia obtenida de un resultado significativo en $p < . 05 32.$

16.3.6.1 La prueba de hipótesis como toma de decisiones: el enfoque de Neyman-Pearson

Mientras que Fisher pensó que el valor p podría aportar evidencia respecto a una hipótesis específica, los estadísticos Jerzy Neyman y Egon Pearson discreparon vehementemente. En cambio, propusieron que pensemos en las pruebas de hipótesis en términos de su tasa de error a largo plazo:

“ninguna prueba basada en una teoría de la probabilidad puede por sí misma proporcionar alguna evidencia valiosa de la verdad o falsedad de una hipótesis. Pero podemos mirar el propósito de las pruebas desde otro punto de vista. Sin esperar saber si cada hipótesis separada es verdadera o falsa, podemos buscar reglas que rijan nuestro comportamiento con respecto a ellas, en seguimiento de lo cual aseguramos que, a largo plazo de la experiencia, a menudo no nos equivocaremos” (Neyman y Pearson 1933)

Es decir: No podemos saber qué decisiones específicas son correctas o incorrectas, pero si seguimos las reglas, al menos podemos saber con qué frecuencia nuestras decisiones van a estar equivocadas en promedio.

Para entender el marco de toma de decisiones que Neyman y Pearson desarrollaron, primero debemos discutir la toma de decisiones estadísticas en términos de los tipos de resultados que pueden ocurrir. Hay dos posibles estados de realidad ( $H$ es cierto, o $H$ es falso), y dos posibles decisiones (rechazar $H$ , o no rechazar $H$ ). Hay dos formas en las que podemos tomar una decisión correcta:

Podemos decidir rechazar $H$ cuando es falso (en el lenguaje de la teoría de la decisión, llamamos a esto un hit)
Podemos no rechazar $H$ cuando es cierto (a esto lo llamamos un rechazo correcto)

También hay dos tipos de errores que podemos cometer:

Podemos decidir rechazar $H$ cuando en realidad es cierto (llamamos a esto una falsa alarma, o error de Tipo I)
Podemos no rechazar $H$ cuando en realidad es falso (llamamos a esto un error de error, o tipo II)

Neyman y Pearson acuñaron dos términos para describir la probabilidad de estos dos tipos de errores a largo plazo:

P (Error tipo I) = $\ alfa$
P (Error tipo II) = $\ beta$

Es decir, si establecemos $α 18.3, que es el complemento del error Tipo II.$

16.3.7 ¿Qué significa un resultado significativo?

Existe mucha confusión sobre lo que realmente significan los valores p (Gigerenzer, 2004). Digamos que hacemos un experimento comparando las medias entre condiciones, y encontramos una diferencia con un valor p de .01. Hay una serie de posibles interpretaciones.

16.3.7.1 ¿Significa que la probabilidad de que la hipótesis nula sea cierta es .01?

No. Recuerde que en las pruebas de hipótesis nulas, el valor p es la probabilidad de los datos dada la hipótesis nula ( $P (Datos|H_0)$ ). No justifica conclusiones sobre la probabilidad de la hipótesis nula dados los datos ( $P (H_0|Datos)$ ). Volveremos a esta pregunta cuando discutamos la inferencia bayesiana en un capítulo posterior, ya que el teorema de Bayes nos permite invertir la probabilidad condicional de una manera que nos permite determinar esta última probabilidad.

16.3.7.2 ¿Significa que la probabilidad de que esté tomando la decisión equivocada es .01?

No. Esto sería $P (H_0|Datos)$ , pero recuerde como anteriormente que los valores p son probabilidades de datos bajo $H$ , no probabilidades de hipótesis.

16.3.7.3 ¿Significa que si volvieras a ejecutar el estudio, obtendrías el mismo resultado el 99% del tiempo?

No. El valor p es una declaración sobre la probabilidad de un conjunto de datos en particular bajo el nulo; no nos permite hacer inferencias sobre la probabilidad de eventos futuros como la replicación.

16.3.7.4 ¿Significa que has encontrado un efecto significativo?

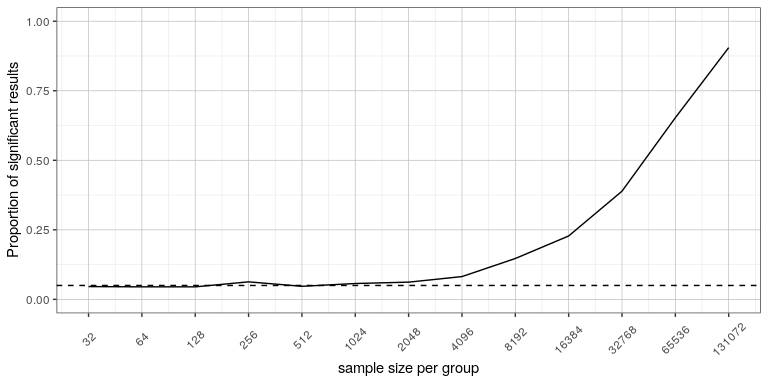
No. Existe una distinción importante entre significancia estadística y significación práctica. Como ejemplo, digamos que realizamos un ensayo controlado aleatorizado para examinar el efecto de una dieta particular sobre el peso corporal, y encontramos un efecto estadísticamente significativo en p<.05. Lo que esto no nos dice es cuánto peso se perdió realmente, a lo que nos referimos como el tamaño del efecto (para ser discutido con más detalle en el Capítulo 18). Si pensamos en un estudio de pérdida de peso, entonces probablemente no pensemos que la pérdida de diez onzas (es decir, el peso de una bolsa de papas fritas) sea prácticamente significativa. Veamos nuestra capacidad para detectar una diferencia significativa de 1 onza a medida que aumenta el tamaño de la muestra.

La Figura 16.7 muestra cómo aumenta la proporción de resultados significativos a medida que aumenta el tamaño de la muestra, de tal manera que con un tamaño de muestra muy grande (alrededor de 262,000 sujetos totales), encontraremos un resultado significativo en más del 90% de los estudios cuando hay una pérdida de peso de 1 onza. Si bien estos son estadísticamente significativos, la mayoría de los médicos no considerarían que una pérdida de peso de una onza sea práctica o clínicamente significativa. Exploraremos esta relación con más detalle cuando volvamos al concepto de poder estadístico en la Sección 18.3, pero ya debería quedar claro a partir de este ejemplo que la significación estadística no es necesariamente indicativa de significación práctica.

La proporción de significantes resulta para un cambio muy pequeño (1 onza, que es aproximadamente .001 desviaciones estándar) en función del tamaño de la muestra. — Figura 16.7: La proporción de resultados significantes para un cambio muy pequeño (1 onza, que es aproximadamente 0,001 desviaciones estándar) en función del tamaño de la muestra.