20.6: Pruebas de Hipótesis Bayesianas

Última actualización
Guardar como PDF

Page ID: 150576

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Habiendo aprendido a realizar la estimación bayesiana, ahora recurrimos al uso de métodos bayesianos para la prueba de hipótesis. Digamos que hay dos políticos que difieren en sus creencias sobre si el público está a favor de un impuesto extra para apoyar a los parques nacionales. El Senador Smith piensa que sólo el 40% de la gente está a favor del impuesto, mientras que el Senador Jones piensa que el 60% de la gente está a favor. Hacen arreglos para que se haga una encuesta para probar esto, que pregunta a 1000 personas seleccionadas al azar si apoyan dicho impuesto. Los resultados son que 490 de las personas de la muestra encuestada estuvieron a favor del impuesto. Con base en estos datos, nos gustaría saber: ¿Los datos respaldan las afirmaciones de un senador sobre el otro, y por cuánto? Podemos probar esto usando un concepto conocido como el factor Bayes, que cuantifica qué hipótesis es mejor comparando qué tan bien cada uno predice los datos observados.

20.6.1 Factores de Bayes

El factor Bayes caracteriza la probabilidad relativa de los datos bajo dos hipótesis diferentes. Se define como:

$BF =\ frac {p (datos|H_1)} {p (datos|H_2)}$

para dos hipótesis $H$ y $H$ . En el caso de nuestros dos senadores, sabemos calcular la probabilidad de los datos bajo cada hipótesis utilizando la distribución binomial. Pondremos al Senador Smith en el numerador y al Senador Jones en el denominador, para que un valor mayor que uno refleje mayores evidencias para el Senador Smith, y un valor menor que uno reflejará mayores evidencias para el Senador Jones. El Factor Bayes resultante (3325.26) proporciona una medida de las pruebas que proporcionan los datos respecto a las dos hipótesis -en este caso, nos dice que los datos apoyan al Senador Smith más de 3000 veces más fuertemente de lo que apoyan al senador Jones.

20.6.2 Factores de Bayes para hipótesis estadísticas

En el ejemplo anterior teníamos predicciones específicas de cada senador, cuya probabilidad podríamos cuantificar usando la distribución binomial. Sin embargo, en el análisis de datos reales generalmente debemos lidiar con la incertidumbre sobre nuestros parámetros, lo que complica el factor Bayes. Sin embargo, a cambio ganamos la capacidad de cuantificar la cantidad relativa de evidencia a favor de las hipótesis nulas versus alternativas.

Digamos que somos un investigador médico realizando un ensayo clínico para el tratamiento de la diabetes, y deseamos saber si un medicamento en particular reduce la glucosa en sangre en comparación con el placebo. Reclutamos a un grupo de voluntarios y los asignamos aleatoriamente al grupo de fármaco o placebo, y medimos el cambio en la hemoglobina A1C (un marcador de los niveles de glucosa en sangre) en cada grupo durante el periodo en el que se administró el fármaco o placebo. Lo que queremos saber es: ¿Hay alguna diferencia entre el medicamento y el placebo?

Primero, generemos algunos datos y los analicemos usando pruebas de hipótesis nulas (ver Figura 20.5). Luego vamos a realizar una prueba t de muestras independientes, que muestra que existe una diferencia significativa entre los grupos:

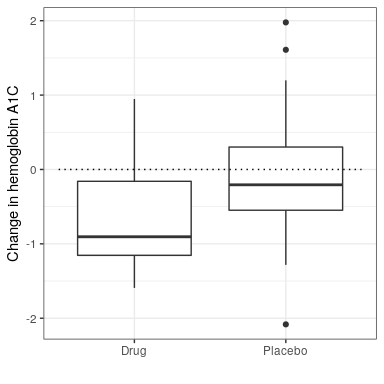
Figura 20.5: Gráfica de caja que muestra datos para grupos de fármaco y placebo.

## 
##  Welch Two Sample t-test
## 
## data:  hbchange by group
## t = 2, df = 32, p-value = 0.02
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  0.11  Inf
## sample estimates:
## mean in group 0 mean in group 1 
##          -0.082          -0.650

Esta prueba nos dice que existe una diferencia significativa entre los grupos, pero no cuantifica con qué fuerza la evidencia apoya las hipótesis nulas versus alternativas. Para medirlo, podemos calcular un factor Bayes usando la función TTestBF del paquete BayesFactor en R:

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf    : 3.4  ±0%
## [2] Alt., r=0.707 !(0<d<Inf) : 0.12 ±0%
## 
## Against denominator:
##   Null, mu1-mu2 = 0 
## ---
## Bayes factor type: BFindepSample, JZS

Nos interesa particularmente el Factor Bayes para un efecto mayor a cero, el cual aparece listado en la línea marcada “[1]” en el reporte. El factor Bayes aquí nos dice que la hipótesis alternativa (es decir, que la diferencia es mayor que cero) es aproximadamente 3 veces más probable que la hipótesis de punto nulo (es decir, una diferencia media de exactamente cero) dados los datos. Así, si bien el efecto es significativo, la cantidad de evidencia que nos proporciona a favor de la hipótesis alternativa es bastante débil.

20.6.2.1 Pruebas unilaterales

Generalmente estamos menos interesados en probar contra la hipótesis nula de un valor puntual específico (por ejemplo, diferencia de medias = 0) que en probar contra una hipótesis nula direccional (por ejemplo, que la diferencia es menor o igual a cero). También podemos realizar una prueba direccional (o unilateral) utilizando los resultados del análisis TTestBF, ya que proporciona dos factores Bayes: uno para la hipótesis alternativa de que la diferencia de medias es mayor que cero, y otro para la hipótesis alternativa de que la diferencia de medias es menor que cero. Si queremos evaluar la evidencia relativa de un efecto positivo, podemos calcular un factor de Bayes comparando la evidencia relativa de un efecto positivo versus un efecto negativo simplemente dividiendo los dos factores Bayes devueltos por la función:

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 0<d<Inf : 29 ±0%
## 
## Against denominator:
##   Alternative, r = 0.707106781186548, mu =/= 0 !(0<d<Inf) 
## ---
## Bayes factor type: BFindepSample, JZS

Ahora vemos que el factor Bayes para un efecto positivo versus un efecto negativo es sustancialmente mayor (casi 30).

20.6.2.2 Interpretación de factores Bayes

¿Cómo sabemos si un factor Bayes de 2 o 20 es bueno o malo? Existe una guía general para la interpretación de los factores Bayes sugerida por Kass & Rafferty (1995):

BF	Fuerza de la evidencia
1 a 3	no vale más que una simple mención
3 a 20	positivo
20 a 150	fuerte
>150	muy fuerte

En base a esto, aunque el resultado estadístico es significativo, la cantidad de evidencia a favor de la hipótesis alternativa vs. punto nulo es lo suficientemente débil como para que ni siquiera valga la pena mencionar, mientras que la evidencia para la hipótesis direccional es relativamente fuerte.

20.6.3 Evaluación de la evidencia para la hipótesis nula

Debido a que el factor Bayes es comparar evidencia para dos hipótesis, también nos permite evaluar si hay evidencia a favor de la hipótesis nula, lo que no podríamos hacer con la prueba estándar de hipótesis nula (porque comienza con la suposición de que el nulo es verdadero). Esto puede ser muy útil para determinar si un resultado no significativo realmente proporciona evidencia sólida de que no hay efecto, o en su lugar solo refleja evidencia débil en general.