24.4: Correlación y causalidad

Cuando decimos que una cosa causa otra, ¿a qué nos referimos? Hay una larga historia en la filosofía de discusión sobre el significado de la causalidad, pero en las estadísticas una manera que comúnmente pensamos de la causalidad es en términos de control experimental. Es decir, si pensamos que el factor X causa el factor Y, entonces manipular el valor de X también debería cambiar el valor de Y.

En medicina, existe un conjunto de ideas conocidas como postulados de Koch que históricamente se han utilizado para determinar si un organismo en particular causa una enfermedad. La idea básica es que el organismo debe estar presente en las personas con la enfermedad, y no presente en quienes no la tienen —así, un tratamiento que elimine al organismo también debería eliminar la enfermedad. Además, infectar a alguien con el organismo debería hacer que contraiga la enfermedad. Un ejemplo de ello se vio en el trabajo del doctor Barry Marshall, quien tenía la hipótesis de que las úlceras estomacales eran causadas por una bacteria (Helicobacter pylori). Para demostrarlo, se infectó con la bacteria, y poco después desarrolló una severa inflamación en el estómago. Después se trató con un antibiótico, y su estómago pronto se recuperó. Posteriormente obtuvo el Premio Nobel de Medicina por esta obra.

A menudo nos gustaría probar hipótesis causales pero en realidad no podemos hacer un experimento, ya sea porque es imposible (“¿Cuál es la relación entre las emisiones humanas de carbono y el clima de la tierra?”) o poco ético (“¿Cuáles son los efectos del abuso severo en el desarrollo cerebral infantil?”). Sin embargo, aún podemos recopilar datos que puedan ser relevantes para esas preguntas. Por ejemplo, en este último ejemplo, potencialmente podemos recopilar datos de niños que han sido abusados así como de aquellos que no lo han hecho, y luego podemos preguntar si su desarrollo cerebral es diferente.

Digamos que hicimos tal análisis, y encontramos que los niños maltratados tenían un peor desarrollo cerebral que los niños no abusados. ¿Demostraría esto que el abuso causa un peor desarrollo cerebral? No. Siempre que observamos una asociación estadística entre dos variables, ciertamente es posible que una de esas dos variables cause la otra. Sin embargo, también es posible que ambas variables estén siendo influenciadas por una tercera variable; en este ejemplo, podría ser que el abuso infantil esté asociado con el estrés familiar, lo que también podría causar un peor desarrollo cerebral a través de un menor compromiso intelectual, estrés alimentario, o muchas otras posibles vías. El punto es que una correlación entre dos variables generalmente nos dice que algo probablemente esté causando otra cosa, pero no nos dice qué está causando qué.

24.4.1 Gráficas causales

Una manera útil de describir las relaciones causales entre variables es a través de una gráfica causal, que muestra las variables como círculos y las relaciones causales entre ellas como flechas. Por ejemplo, la Figura 24.4 muestra las relaciones causales entre el tiempo de estudio y dos variables que creemos que deberían verse afectadas por el mismo: las calificaciones de los exámenes y los tiempos de finalización del examen.

Sin embargo, en realidad los efectos en el tiempo de finalización y las calificaciones no se deben directamente a la cantidad de tiempo dedicado a estudiar, sino a la cantidad de conocimiento que el estudiante adquiere al estudiar. Normalmente diríamos que el conocimiento es una variable latente —es decir, no podemos medirlo directamente pero podemos verlo reflejado en variables que podemos medir (como las calificaciones y los tiempos de finalización). La Figura 24.5 muestra esto.

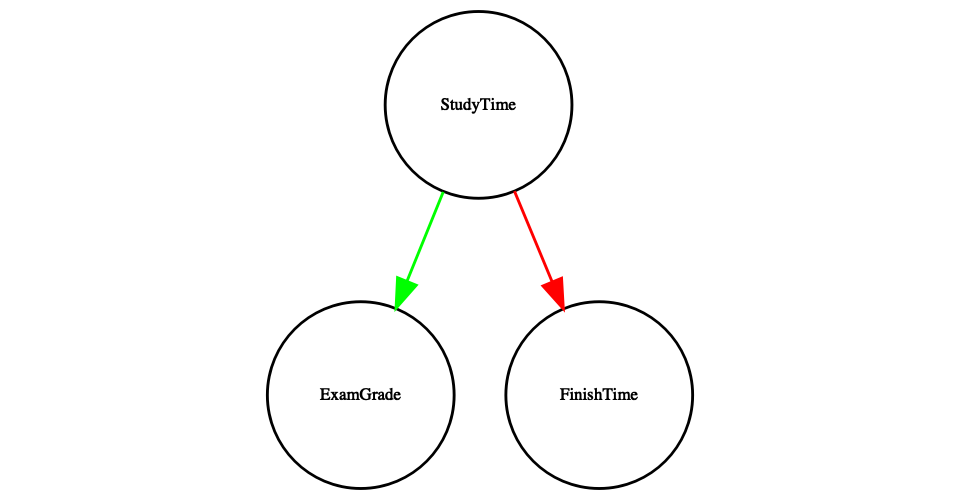
Figura 24.4: Gráfica que muestra las relaciones causales entre tres variables: tiempo de estudio, calificaciones de examen y tiempo de finalización del examen. Una flecha verde representa una relación positiva (es decir, más tiempo de estudio hace que las calificaciones del examen aumenten), y una flecha roja representa una relación negativa (es decir, más tiempo de estudio hace que el examen termine más rápido).

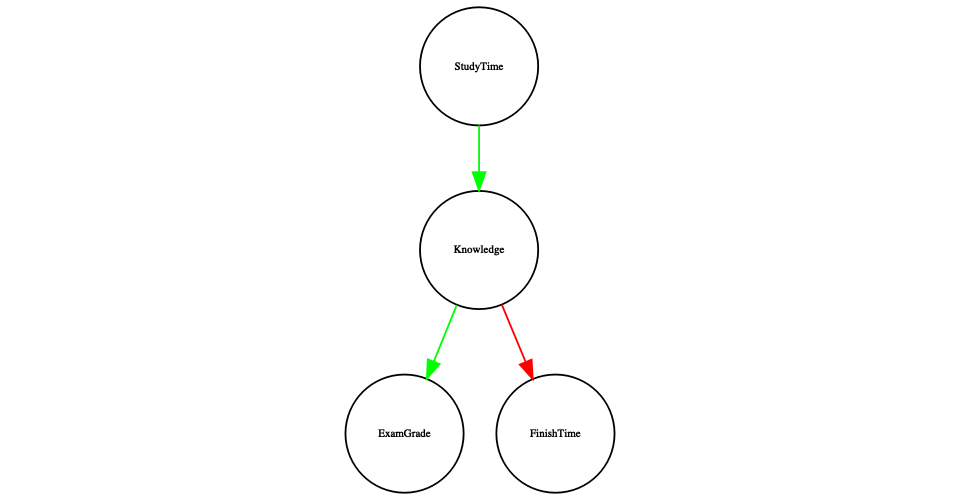
Figura 24.5: Una gráfica que muestra las mismas relaciones causales que las anteriores, pero ahora también muestra la variable latente (conocimiento) usando una caja cuadrada.

Aquí diríamos que el conocimiento media la relación entre el tiempo de estudio y los grados/tiempos de finalización. Eso significa que si fuéramos capaces de mantener el conocimiento constante (por ejemplo, administrando un medicamento que provoca el olvido inmediato), entonces la cantidad de tiempo de estudio ya no debería tener un efecto en las calificaciones y los tiempos de finalización.

Tenga en cuenta que si simplemente medimos las calificaciones de los exámenes y los tiempos de finalización generalmente veríamos una relación negativa entre ellos, porque las personas que terminan los exámenes más rápido en general obtienen las calificaciones más altas. Sin embargo, si tuviéramos que interpretar esta correlación como una relación causal, esto nos diría que para obtener mejores calificaciones, ¡en realidad deberíamos terminar el examen más rápido! Este ejemplo muestra lo difícil que puede ser la inferencia de causalidad a partir de datos no experimentales.

Dentro de la estadística y el aprendizaje automático, existe una comunidad de investigación muy activa que actualmente estudia la cuestión de cuándo y cómo podemos inferir relaciones causales a partir de datos no experimentales. Sin embargo, estos métodos a menudo requieren suposiciones fuertes, y generalmente deben usarse con mucha precaución.