24.3: Covarianza y Correlación

Última actualización
Guardar como PDF

Page ID: 150530

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Una forma de cuantificar la relación entre dos variables es la covarianza. Recuerde que la varianza para una sola variable se calcula como la diferencia cuadrada promedio entre cada punto de datos y la media:

$s^2 =\ frac {\ suma_ {i=1} ^n (x_i -\ bar {x}) ^2} {N - 1}$

Esto nos dice a qué distancia está cada observación de la media, en promedio, en unidades cuadradas. La covarianza nos indica si existe una relación entre las desviaciones de dos variables diferentes a través de las observaciones. Se define como:

$covarianza =\ frac {\ suma_ {i=1} ^n (x_i -\ bar {x}) (y_i -\ bar {y})} {N - 1}$

Este valor estará lejos de cero cuando x e y estén ambos muy desviados de la media; si están desviados en la misma dirección entonces la covarianza es positiva, mientras que si son desviados en direcciones opuestas la covarianza es negativa. Veamos primero un ejemplo de juguete. Los datos se muestran en la tabla, junto con sus desviaciones individuales de la media y sus productos cruzados.

Cuadro 24.1: Datos para ejemplo de covarianza de juguete
x	y	y_dev	x_dev	crossproduct
3	5	-3.6	-4.6	16.56
5	4	-4.6	-2.6	11.96
8	7	-1.6	0.4	-0.64
10	10	1.4	2.4	3.36
12	17	8.4	4.4	36.96

La covarianza es simplemente la media de los productos cruzados, que en este caso es 17.05. No solemos usar la covarianza para describir las relaciones entre variables, ya que varía con el nivel general de varianza en los datos. En cambio, usualmente usaríamos el coeficiente de correlación (a menudo referido como correlación de Pearson después del estadístico Karl Pearson). La correlación se calcula escalando la covarianza por las desviaciones estándar de las dos variables:

$r =\ frac {covarianza} {s_xs_y} =\ frac {\ suma_ {i=1} ^n (x_i -\ bar {x}) (y_i -\ bar {y})} {(N - 1) s_x s_y}$ En este caso, el valor es0.89. También podemos calcular el valor de correlación fácilmente usando la función cor () en R, en lugar de calcularlo a mano.

El coeficiente de correlación es útil porque varía entre -1 y 1 independientemente de la naturaleza de los datos; de hecho, ya discutimos el coeficiente de correlación anteriormente en la discusión de los tamaños de efecto. Como vimos en el capítulo anterior sobre tamaños de efecto, una correlación de 1 indica una relación lineal perfecta, una correlación de -1 indica una relación negativa perfecta y una correlación de cero indica que no hay relación lineal.

24.3.1 Prueba de hipótesis para correlaciones

El valor de correlación de 0.42 parece indicar una relación razonablemente fuerte entre los crímenes de odio y la desigualdad de ingresos, pero también podemos imaginar que esto podría ocurrir por casualidad aunque no haya relación alguna. Podemos probar la hipótesis nula de que la correlación es cero, usando una ecuación simple que nos permite convertir un valor de correlación en un estadístico t:

$t_{r}=\frac{r \sqrt{N-2}}{\sqrt{1-r^{2}}}$

Bajo la hipótesis nula $H_0:r=0$ , esta estadística se distribuye como una distribución t con $N - 2$ grados de libertad. Podemos calcular esto usando la función cor.test () en R:

## 
##  Pearson's product-moment correlation
## 
## data:  hateCrimes$avg_hatecrimes_per_100k_fbi and hateCrimes$gini_index
## t = 3, df = 48, p-value = 0.002
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.16 0.63
## sample estimates:
##  cor 
## 0.42

Esta prueba muestra que la probabilidad de un valor r este extremo o más es bastante baja, por lo que rechazaríamos la hipótesis nula de $r=0$ . Tenga en cuenta que esta prueba asume que ambas variables están normalmente distribuidas.

También podríamos probar esto por aleatorización, en la que aleatorizamos repetidamente los valores de una de las variables y calculamos la correlación, y luego comparamos nuestro valor de correlación observado con esta distribución nula para determinar qué tan probable sería nuestro valor observado bajo la hipótesis nula. Los resultados se muestran en la Figura 24.2. El valor p calculado mediante aleatorización es razonablemente similar a la respuesta dada por la prueba t.

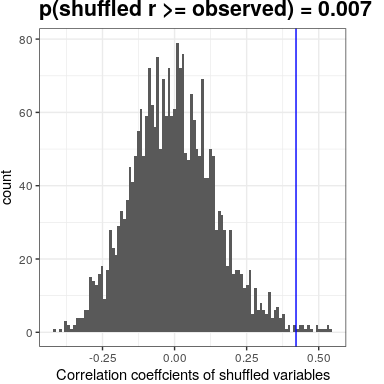
Histograma de valores de correlación bajo la hipótesis nula, obtenidos por barajado de valores. El valor observado se denota por la línea azul.

Figura 24.2: Histograma de valores de correlación bajo la hipótesis nula, obtenidos por barajado de valores. El valor observado se denota por la línea azul.

También podríamos usar la inferencia bayesiana para estimar la correlación; ver el Apéndice para más información sobre esto.

24.3.2 Correlaciones robustas

Es posible que hayas notado algo un poco extraño en la Figura 24.1 —uno de los puntos de datos (el del Distrito de Columbia) parecía estar bastante separado de los demás. Nos referimos a esto como un valor atípico, y el coeficiente de correlación estándar es muy sensible a los valores atípicos. Por ejemplo, en la Figura 24.3 podemos ver cómo un único punto de datos periféricos puede provocar un valor de correlación positiva muy alto, incluso cuando la relación real entre los otros puntos de datos es perfectamente negativa.

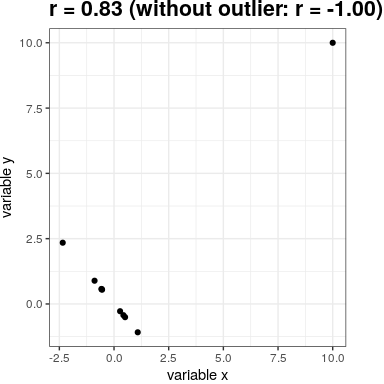
Un ejemplo simulado de los efectos de los valores atípicos sobre la correlación. Sin el valor atípico, el resto de los puntos de datos tienen una correlación negativa perfecta, pero el valor atípico único cambia el valor de correlación a altamente positivo.

Figura 24.3: Un ejemplo simulado de los efectos de los valores atípicos sobre la correlación. Sin el valor atípico, el resto de los puntos de datos tienen una correlación negativa perfecta, pero el valor atípico único cambia el valor de correlación a altamente positivo.

Una forma de abordar los valores atípicos es calcular la correlación en las filas de los datos después de ordenarlos, en lugar de en los propios datos; esto se conoce como la correlación de Spearman. Mientras que la correlación de Pearson para el ejemplo de la Figura 24.3 fue de 0.83, la correlación de Spearman es -0.45, mostrando que la correlación de rango reduce el efecto del valor atípico.

Podemos calcular la correlación de rango en los datos de delitos de odio usando la función cor.test:

## 
##  Spearman's rank correlation rho
## 
## data:  hateCrimes$avg_hatecrimes_per_100k_fbi and hateCrimes$gini_index
## S = 20146, p-value = 0.8
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##   rho 
## 0.033

Ahora vemos que la correlación ya no es significativa (y de hecho está muy cerca de cero), lo que sugiere que las afirmaciones de la entrada del blog FiveThirtyEight pueden haber sido incorrectas debido al efecto del valor atípico.