26.1: Regresión lineal

También podemos usar el modelo lineal general para describir la relación entre dos variables y para decidir si esa relación es estadísticamente significativa; además, el modelo nos permite predecir el valor de la variable dependiente dado algunos nuevos valores de la (s) variable (s) independiente (s). Lo más importante es que el modelo lineal general nos permitirá construir modelos que incorporen múltiples variables independientes, mientras que la correlación solo puede decirnos sobre la relación entre dos variables individuales.

La versión específica del GLM que usamos para esto se conoce como regresión lineal. El término regresión fue acuñado por Francis Galton, quien había señalado que cuando comparaba a los padres y a sus hijos en algún rasgo (como la altura), los hijos de padres extremos (es decir, los padres muy altos o muy bajos) generalmente se acercaban más a la media que sus padres. Este es un punto sumamente importante al que volvemos a continuación.

La versión más simple del modelo de regresión lineal (con una sola variable independiente) se puede expresar de la siguiente manera:

$$y = x *\ beta_x +\ beta_0 +\ épsilon$$El$\ beta_x$valor nos dice cuánto esperaríamos que y cambie dado un cambio de una unidad en x. La intercepción$\ beta_0$es una compensación general, que nos dice qué valor esperaríamos y tener cuando$x=0$; tal vez recuerde de nuestra discusión sobre modelización temprana que esto es importante para modelar la magnitud general de los datos, incluso si$x$nunca alcanza realmente un valor de cero. El término de error$\ épsilon$se refiere a lo que queda una vez que el modelo ha estado en forma. Si queremos saber cómo predecir y (que llamamos$\ sombrero {y}$), entonces podemos dejar caer el término de error:

$$\hat{y}=x*{\beta }_x+{\beta }_0$$

Figura 26.2: La solución de regresión lineal para los datos de tiempo de estudio se muestra en la línea continua El valor de la intercepción es equivalente al valor predicho de la variable y cuando la variable x es igual a cero; esto se muestra con una línea punteada. El valor de beta es igual a la pendiente de la línea, es decir, cuánto y cambia para un cambio unitario en x Esto se muestra esquemáticamente en las líneas discontinuas, las cuales muestran el grado de aumento de grado para una sola unidad de aumento en el tiempo de estudio.

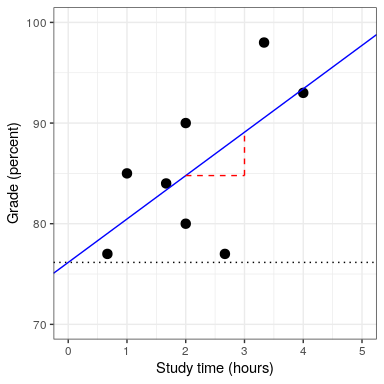
No entraremos en los detalles de cómo se estiman realmente la mejor pendiente e intercepción de ajuste a partir de los datos; si está interesado, los detalles están disponibles en el Apéndice.

26.1.1 Regresión a la media

El concepto de regresión a la media fue una de las contribuciones esenciales de Galton a la ciencia, y sigue siendo un punto crítico a entender cuando interpretamos los resultados de los análisis de datos experimentales. Digamos que queremos estudiar los efectos de una intervención lectora sobre el desempeño de los lectores pobres. Para probar nuestra hipótesis, podríamos ingresar a una escuela y reclutar a aquellos individuos en el 25% inferior de la distribución en alguna prueba de lectura, administrar la intervención y luego examinar su desempeño. Digamos que la intervención en realidad no tiene ningún efecto, de tal manera que las puntuaciones de lectura para cada individuo son simplemente muestras independientes de una distribución normal. Podemos simular esto:

Cuadro 26.1: Puntajes de lectura para la Prueba 1 (que es menor, porque fue la base para seleccionar a los estudiantes) y la Prueba 2 (que es mayor porque no estaba relacionada con la Prueba 1).

	Score
Prueba 1	88
Prueba 2	101

Si observamos la diferencia entre el rendimiento medio de la prueba en la primera y la segunda prueba, parece que la intervención ha ayudado sustancialmente a estos alumnos, ¡ya que sus puntuaciones han subido en más de diez puntos en la prueba! Sin embargo, sabemos que de hecho los estudiantes no mejoraron en absoluto, ya que en ambos casos los puntajes simplemente se seleccionaron de una distribución normal aleatoria. Lo que ha ocurrido es que algunos sujetos puntuaron mal en la primera prueba simplemente por azar azar. Si seleccionamos solo esas materias sobre la base de sus primeros puntajes de prueba, se garantiza que retrocedan hacia la media de todo el grupo en la segunda prueba, aunque no haya efecto del entrenamiento. Esta es la razón por la que necesitamos un grupo control no tratado para interpretar cualquier cambio en la lectura a lo largo del tiempo; de lo contrario, es probable que nos engañen por regresión a la media.

26.1.2 La relación entre correlación y regresión

Existe una estrecha relación entre los coeficientes de correlación y los coeficientes de regresión. Recuerde que el coeficiente de correlación de Pearson se calcula como la relación de la covarianza y el producto de las desviaciones estándar de x e y:

$$\ hat {r} =\ frac {covariance_ {xy}} {s_x * s_y}$$mientras que la regresión beta se calcula como:

$$\ hat {\ beta} =\ frac {covariance_ {xy}} {s_x*s_x}$$

A partir de estas dos ecuaciones, podemos derivar la relación entre$\ sombrero {r}$y$\ hat {beta}$:

$$covariance_ {xy} =\ hat {r} * s_x * s_y$$

$$\ sombrero {\ beta_x} =\ frac {\ sombrero {r} * s_x * s_y} {s_x * s_x} = r *\ frac {s_y} {s_x}$$Es decir, la pendiente de regresión es igual al valor de correlación multiplicado por la relación de desviaciones estándar de y y x Una cosa que esto nos dice es que cuando las desviaciones estándar de x e y son las mismas (por ejemplo, cuando los datos se han convertido a puntuaciones Z), entonces la estimación de correlación es igual a la estimación de pendiente de regresión.

26.1.3 Errores estándar para modelos de regresión

Si queremos hacer inferencias sobre las estimaciones de los parámetros de regresión, entonces también necesitamos una estimación de su variabilidad. Para calcular esto, primero necesitamos calcular la varianza residual o varianza de error para el modelo, es decir, cuánta variabilidad en la variable dependiente no es explicada por el modelo. Podemos calcular los residuos del modelo de la siguiente manera:

$$residual = y -\ hat {y} = y - (x*\ hat {\ beta_x} +\ hat {\ beta_0})$$Luego calculamos la suma de errores cuadrados (SSE):

$$SS_ {error} =\ suma_ {i=1} ^n {(y_i -\ hat {y_i}) ^2} =\ suma_ {i=1} ^n {residuales^2}$$y a partir de esto calculamos el error cuadrático medio:

$$MS_ {error} =\ frac {SS_ {error}} {df} =\ frac {\ suma_ {i=1} ^n {(y_i -\ hat {y_i}) ^2}} {N - p}$$donde los grados de libertad ($df$) se determinan restando el número de parámetros estimados (2 en este caso:$\ sombrero {\ beta_x}$y$\ sombrero {\ beta_0}$) del número de observaciones ($N$). Una vez que tenemos el error cuadrático medio, podemos calcular el error estándar para el modelo como:

$$SE_ {modelo} =\ sqrt {MS_ {error}}$$

Para obtener el error estándar para una estimación de parámetro de regresión específica,$SE$, necesitamos reescalar el error estándar del modelo por la raíz cuadrada de la suma de cuadrados de la variable X:

$$SE_ {\ beta_x} =\ frac {SE_ {modelo}} {\ sqrt$$

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Estadisticas/Estadisticas_Introductorias/Libro:_Pensamiento_estadístico_para_el_siglo_XXI_(Poldrack)/26:_El_modelo_lineal_general/26.01:_Regresión_lineal), /content/body/section[3]/div/p[7]/math/semantics/annotation/span, line 1, column 1

26.1.4 Pruebas estadísticas para parámetros de regresión

Una vez que tenemos las estimaciones de parámetros y sus errores estándar, podemos calcular un estadístico t para decirnos la probabilidad de las estimaciones de parámetros observados en comparación con algún valor esperado bajo la hipótesis nula. En este caso probaremos contra la hipótesis nula de no efecto (i.e.$\ beta=0$):

$$\ begin {array} {c} t_ {N - p} =\ frac {\ hat {\ beta} -\ beta_ {esperado}} {SE_ {\ hat {\ beta}}\\ t_ {N - p} =\ frac {\ hat {\ beta} - 0} {SE_ {\ hat {\ beta}}\\ t_ {N - p} = ac {\ hat {\ beta}} {SE_ {\ hat {\ beta}}\ end {array}$$

En R, no necesitamos computar estos a mano, ya que nos son devueltos automáticamente por la función lm ():

## 
## Call:
## lm(formula = grade ~ studyTime, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.656  -2.719   0.125   4.703   7.469 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    76.16       5.16   14.76  6.1e-06 ***
## studyTime       4.31       2.14    2.01    0.091 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.4 on 6 degrees of freedom
## Multiple R-squared:  0.403,  Adjusted R-squared:  0.304 
## F-statistic: 4.05 on 1 and 6 DF,  p-value: 0.0907

En este caso vemos que la intercepción es significativamente diferente de cero (lo cual no es muy interesante) y que el efecto del Tiempo de Estudio sobre las calificaciones es marginalmente significativo (p = .09).

26.1.5 Cuantificación de la bondad de ajuste del modelo

A veces es útil cuantificar qué tan bien se ajusta el modelo a los datos en general, y una forma de hacerlo es preguntar qué tanto de la variabilidad en los datos se explica por el modelo. Esto se cuantifica usando un valor llamado$R$(también conocido como el coeficiente de determinación). Si solo hay una variable x, entonces esto es fácil de calcular simplemente al cuadrado del coeficiente de correlación:

$$R^2 = r^2$$En el caso de nuestro ejemplo de tiempo de estudio,$R$= 0.4, lo que significa que hemos contabilizado alrededor del 40% de la varianza en las calificaciones.

De manera más general se nos ocurre$R$como medida de la fracción de varianza en los datos que es contabilizada por el modelo, que se puede calcular dividiendo la varianza en múltiples componentes:

$$SS_ {total} = SS_ {modelo} + SS_ {error}$$donde$SS$es la varianza de los datos ($y$) y$SS$y$SS$se computan como se muestra anteriormente en este capítulo. Usando esto, podemos entonces calcular el coeficiente de determinación como:

$$R^2 =\ frac {SS_ {modelo}} {SS_ {total}} = 1 -\ frac {SS_ {error}} {SS_ {total}}$$

Un pequeño valor de$R$nos dice que aunque el ajuste del modelo sea estadísticamente significativo, solo puede explicar una pequeña cantidad de información en los datos.