26.3: Interacciones entre variables

En el modelo anterior, asumimos que el efecto del tiempo de estudio sobre el grado (es decir, la pendiente de regresión) fue el mismo para ambos grupos. Sin embargo, en algunos casos podríamos imaginar que el efecto de una variable podría diferir dependiendo del valor de otra variable, a la que nos referimos como una interacción entre variables.

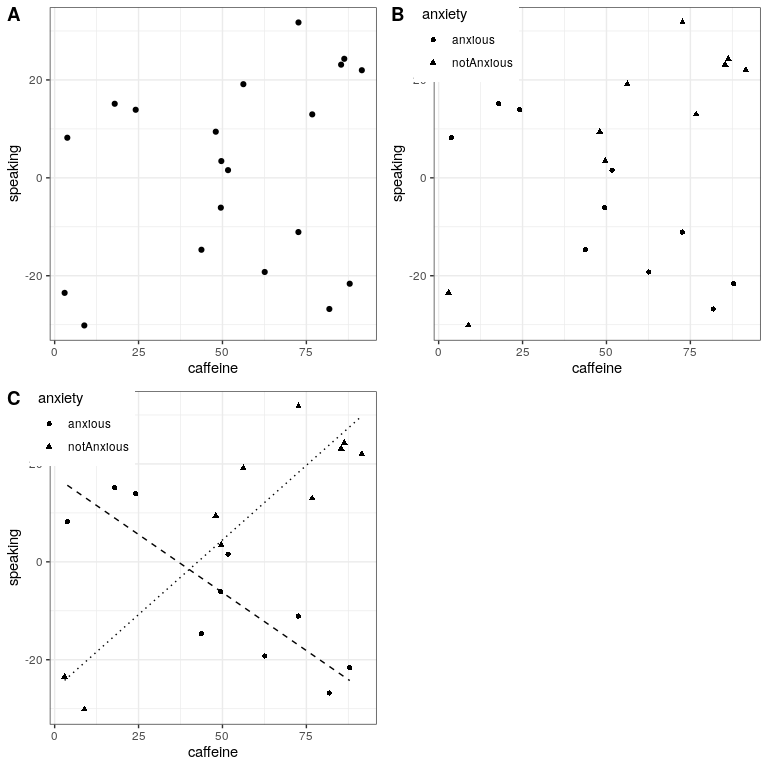
Usemos un nuevo ejemplo que haga la pregunta: ¿Cuál es el efecto de la cafeína en hablar en público? Primero vamos a generar algunos datos y trazarlos. Al observar el panel A de la Figura 26.4, no parece haber una relación, y podemos confirmar que realizando regresión lineal en los datos:

## 
## Call:
## lm(formula = speaking ~ caffeine, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -33.10 -16.02   5.01  16.45  26.98 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)   -7.413      9.165   -0.81     0.43
## caffeine       0.168      0.151    1.11     0.28
## 
## Residual standard error: 19 on 18 degrees of freedom
## Multiple R-squared:  0.0642, Adjusted R-squared:  0.0122 
## F-statistic: 1.23 on 1 and 18 DF,  p-value: 0.281

Pero ahora digamos que encontramos investigaciones que sugieren que las personas ansiosas y no ansiosas reaccionan de manera diferente a la cafeína. Primero trazemos los datos por separado para personas ansiosas y no ansiosas.

Como vemos en el panel B en la Figura 26.4, parece que la relación entre el habla y la cafeína es diferente para los dos grupos, con la cafeína mejorando el rendimiento para las personas sin ansiedad y degradando el rendimiento para las personas con ansiedad. Nos gustaría crear un modelo estadístico que aborde esta cuestión. Primero veamos qué pasa si solo incluimos la ansiedad en el modelo.

## 
## Call:
## lm(formula = speaking ~ caffeine + anxiety, data = df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -32.97  -9.74   1.35  10.53  25.36 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)
## (Intercept)        -12.581      9.197   -1.37     0.19
## caffeine             0.131      0.145    0.91     0.38
## anxietynotAnxious   14.233      8.232    1.73     0.10
## 
## Residual standard error: 18 on 17 degrees of freedom
## Multiple R-squared:  0.204,  Adjusted R-squared:  0.11 
## F-statistic: 2.18 on 2 and 17 DF,  p-value: 0.144

Aquí vemos que no hay efectos significativos ni de la cafeína ni de la ansiedad, lo que puede parecer un poco confuso. El problema es que este modelo está tratando de encajar en la misma línea relativa al hablar con la cafeína para ambos grupos. Si queremos ajustarlos usando líneas separadas, necesitamos incluir una interacción en el modelo, lo que equivale a ajustar diferentes líneas para cada uno de los dos grupos; en R esto se denota con el$*$símbolo.

## 
## Call:
## lm(formula = speaking ~ caffeine + anxiety + caffeine * anxiety, 
##     data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -11.385  -7.103  -0.444   6.171  13.458 
## 
## Coefficients:
##                            Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 17.4308     5.4301    3.21  0.00546 ** 
## caffeine                    -0.4742     0.0966   -4.91  0.00016 ***
## anxietynotAnxious          -43.4487     7.7914   -5.58  4.2e-05 ***
## caffeine:anxietynotAnxious   1.0839     0.1293    8.38  3.0e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.1 on 16 degrees of freedom
## Multiple R-squared:  0.852,  Adjusted R-squared:  0.825 
## F-statistic: 30.8 on 3 and 16 DF,  p-value: 7.01e-07

A partir de estos resultados vemos que hay efectos significativos tanto de la cafeína como de la ansiedad (que llamamos efectos principales) y una interacción entre la cafeína y la ansiedad. El Panel C en la Figura 26.4 muestra las líneas de regresión separadas para cada grupo.

Figura 26.4: A: La relación entre cafeína y hablar en público. B: La relación entre cafeína y hablar en público, con ansiedad representada por la forma de los puntos de datos. C: La relación entre hablar en público y cafeína, incluyendo una interacción con la ansiedad. Esto da como resultado dos líneas que modelan por separado la pendiente para cada grupo (discontinua para ansiosa, punteada para no ansiosa).

A veces queremos comparar el ajuste relativo de dos modelos diferentes, para determinar cuál es un modelo mejor; nos referimos a esto como comparación de modelos. Para los modelos anteriores, podemos comparar la bondad de ajuste del modelo con y sin la interacción, usando el comando anova () en R:

## Analysis of Variance Table
## 
## Model 1: speaking ~ caffeine + anxiety
## Model 2: speaking ~ caffeine + anxiety + caffeine * anxiety
##   Res.Df  RSS Df Sum of Sq    F Pr(>F)    
## 1     17 5639                             
## 2     16 1046  1      4593 70.3  3e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Esto nos dice que hay buena evidencia para preferir el modelo con la interacción sobre el que no tiene interacción. La comparación de modelos es relativamente simple en este caso porque los dos modelos están anidados — uno de los modelos es una versión simplificada del otro modelo. La comparación de modelos con modelos no anidados puede complicarse mucho más.