28.2: Comparando dos medias

Última actualización
Guardar como PDF

Page ID: 150519

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

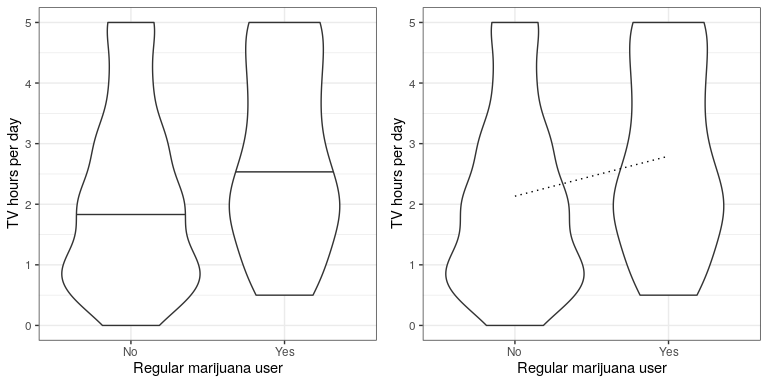
Una pregunta más común que a menudo surge en la estadística es si existe una diferencia entre las medias de dos grupos diferentes. Digamos que nos gustaría saber si los fumadores regulares de marihuana ven más televisión. Podemos hacer esta pregunta usando el conjunto de datos de NHANES; tomemos una muestra de 200 individuos del conjunto de datos y probemos si el número de horas de televisión al día está relacionado con el consumo regular de marihuana. El panel izquierdo de la Figura 28.1 muestra estos datos utilizando una gráfica para violín.

Izquierda: Parcela de violín que muestra distribuciones de televisión viendo separadas por el uso regular de marihuana. Derecha: Gráficas de violín que muestran datos para cada grupo, con una línea punteada que conecta los valores predichos para cada grupo, calculados sobre la base de los resultados del modelo lineal. — Figura 28.1: Izquierda: Parcela de violín que muestra distribuciones de televisión separadas por el consumo regular de marihuana. Derecha: Trazados de violín que muestran datos para cada grupo, con una línea punteada que conecta los valores predichos para cada grupo, calculados sobre la base de los resultados del modelo lineal.

También podemos usar la prueba t de Student para probar diferencias entre dos grupos de observaciones independientes (como vimos en un capítulo anterior); pasaremos más adelante en el capítulo a casos en los que las observaciones no sean independientes. Como recordatorio, la estadística t para la comparación de dos grupos independientes se calcula como:

$t =\ frac {\ bar {X_1} -\ bar {X_2}} {\ sqrt {\ frac {S_1^2} {n_1} +\ frac {S_2^2} {n_2}}}$

donde $\ bar {X} _1$ y $\ bar {X} _2$ son los medios de los dos grupos, $S$ y $S$ son las variaciones para cada uno de los grupos, y $n_1$ y $n_2$ son los tamaños de los dos grupos. Bajo la hipótesis nula de no diferencia entre medias, este estadístico se distribuye de acuerdo con una distribución t con n-2 grados de libertad (ya que hemos calculado dos estimaciones de parámetros, es decir, las medias de los dos grupos). Podemos calcular la prueba t en R usando la función t.test (). En este caso, comenzamos con la hipótesis específica de que fumar marihuana se asocia con una mayor visión de televisión, por lo que usaremos una prueba de una cola. Dado que la función t.test ordena las condiciones alfabéticamente, el grupo “No” viene primero, y así necesitamos probar la hipótesis alternativa de si el primer grupo es menor que el segundo grupo (“Sí”); por esta razón, especificamos 'menos' como nuestra alternativa.

## 
##  Two Sample t-test
## 
## data:  TVHrsNum by RegularMarij
## t = -3, df = 198, p-value = 0.004
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##   -Inf -0.25
## sample estimates:
##  mean in group No mean in group Yes 
##               2.1               2.8

En este caso vemos que existe una diferencia estadísticamente significativa entre los grupos, en la dirección esperada - los fumadores regulares de marihuana ven más televisión.