32.3: La Crisis de Reproducibilidad en la Ciencia

Si bien pensamos que el tipo de comportamiento de fraude que se ve en el caso de Wansink es relativamente raro, se ha vuelto cada vez más claro que los problemas de reproducibilidad están mucho más extendidos en la ciencia de lo que se pensaba anteriormente. Esto quedó claro en 2015, cuando un nutrido grupo de investigadores publicó un estudio en la revista Science titulado “Estimar la reproducibilidad de la ciencia psicológica” (Open Science Collaboration 2015). En este estudio, los investigadores tomaron 100 estudios publicados en psicología e intentaron reproducir los resultados reportados originalmente en los artículos. Sus hallazgos fueron impactantes: Mientras que 97% de los artículos originales habían reportado hallazgos estadísticamente significativos, solo 37% de estos efectos fueron estadísticamente significativos en el estudio de replicación. Aunque estos problemas en la psicología han recibido mucha atención, parecen estar presentes en casi todas las áreas de la ciencia, desde la biología del cáncer (Errington et al. 2014) y la química (Baker 2017) hasta la economía (Christensen y Miguel 2016) y la social ciencias (Camerer et al. 2018).

La crisis de reproducibilidad que surgió después de 2010 fue predicha en realidad por John Ioannidis, un médico de Stanford que escribió un artículo en 2005 titulado “Why most published research findings are false” (Ioannidis 2005). En este artículo, Ioannidis argumentó que el uso de pruebas estadísticas de hipótesis nulas en el contexto de la ciencia moderna conducirá necesariamente a altos niveles de resultados falsos.

32.3.1 Valor predictivo positivo y significancia estadística

El análisis de Ioannidis se centró en un concepto conocido como el valor predictivo positivo, que se define como la proporción de resultados positivos (que generalmente se traduce como “hallazgos estadísticamente significativos”) que son ciertos:

$$PPV =\ frac {p (true\ positive\ result)} {p (true\ positive\ result) + p (false\ positive\ result)}$$Suponiendo que conocemos la probabilidad de que nuestra hipótesis sea cierta ($p (HisTRUE)$), entonces la probabilidad de un verdadero resultado positivo es simplemente$p (HisTRUE)$multiplicado por el poder estadístico del estudio:

$$p (verdadero\ positivo\ resultado) = p (HisTRUE) * (1 -\ beta)$$fueron$\ beta$es la tasa de falsos negativos. La probabilidad de un resultado falso positivo está determinada por$p (HisTRUE)$y la tasa de falsos positivos$\ alfa$:

$$p (falso\ positivo\ resultado) = (1 - p (HisTRUE)) *\ alpha$$

PPV se define entonces como:

$$PPV =\ frac {p (HisTRUE) * (1 -\ beta)} {p (HisTRUE) * (1 -\ beta) + (1 - p (HisTRUE)) *\ alpha}$$

Primero tomemos un ejemplo donde la probabilidad de que nuestra hipótesis sea cierta es alta, digamos 0.8 -aunque tenga en cuenta que en general en realidad no podemos conocer esta probabilidad. Digamos que realizamos un estudio con los valores estándar de$\ alfa=0.05$y$\ beta=0.2$. Podemos calcular el PPV como:

$$PPV =\ frac {0.8 * (1 - 0.2)} {0.8 * (1 - 0.2) + (1 - 0.8) * 0.05} = 0.98$$Esto quiere decir que si encontramos un resultado positivo en un estudio donde es probable que la hipótesis sea verdadera y el poder sea alto, entonces su probabilidad de ser verdadera es alta. Tenga en cuenta, sin embargo, que un campo de investigación donde las hipótesis tienen una probabilidad tan alta de ser ciertas probablemente no sea un campo de investigación muy interesante; ¡la investigación es lo más importante cuando nos dice algo nuevo!

Hagamos el mismo análisis para un campo donde$p (HisTRUE) =0.1$— es decir, la mayoría de las hipótesis que se están probando son falsas. En este caso, PPV es:

$$PPV =\ frac {0.1 * (1 - 0.2)} {0.1 * (1 - 0.2) + (1 - 0.1) * 0.05} = 0.307$$

Esto significa que en un campo donde es probable que la mayoría de las hipótesis estén equivocadas (es decir, un campo científico interesante donde los investigadores están probando hipótesis arriesgadas), ¡incluso cuando encontramos un resultado positivo es más probable que sea falso que verdadero! De hecho, este es solo otro ejemplo del efecto de tasa base que discutimos en el contexto de las pruebas de hipótesis —cuando un resultado es poco probable, entonces es casi seguro que la mayoría de los resultados positivos serán falsos positivos.

Podemos simular esto para mostrar cómo el PPV se relaciona con el poder estadístico, en función de la probabilidad previa de que la hipótesis sea verdadera (ver Figura 32.1)

Figura 32.1: Simulación del valor predictivo posterior en función de la potencia estadística (trazada en el eje x) y la probabilidad previa de que la hipótesis sea verdadera (trazada como líneas separadas).

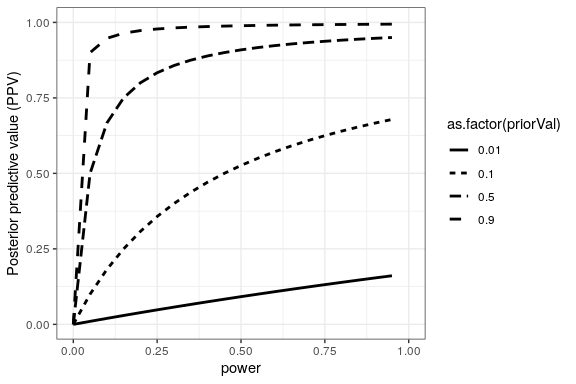
Desafortunadamente, el poder estadístico sigue siendo bajo en muchas áreas de la ciencia (Smaldino y McElreath 2016), lo que sugiere que muchos hallazgos de investigación publicados son falsos.

Un ejemplo divertido de esto fue visto en un artículo de Jonathan Schoenfeld y John Ioannidis, titulado “¿Todo lo que comemos está asociado con el cáncer? Una revisión sistemática del libro de cocina” [scho:ioan:2013]. Examinaron un gran número de artículos que habían evaluado la relación entre los diferentes alimentos y el riesgo de cáncer, y encontraron que 80% de los ingredientes se habían asociado con un mayor o menor riesgo de cáncer. En la mayoría de estos casos, la evidencia estadística fue débil, y cuando los resultados se combinaron entre estudios, el resultado fue nulo.

32.3.2 La maldición del ganador

Otro tipo de error también puede ocurrir cuando la potencia estadística es baja: Nuestras estimaciones del tamaño del efecto serán infladas. Este fenómeno suele ir por el término “maldición del ganador”, que viene de la economía, donde hace referencia al hecho de que para ciertos tipos de subastas (donde el valor es el mismo para todos, como un frasco de cuartos, y las ofertas son privadas), se garantiza que el ganador pagará más de lo que vale el bien. En la ciencia, la maldición del ganador se refiere al hecho de que el tamaño del efecto estimado a partir de un resultado significativo (es decir, un ganador) es casi siempre una sobreestimación del tamaño verdadero del efecto.

Podemos simular esto para ver cómo el tamaño estimado del efecto para resultados significativos se relaciona con el tamaño real del efecto subyacente. Generemos datos para los cuales hay un tamaño de efecto verdadero de 0.2, y estimaremos el tamaño del efecto para aquellos resultados donde se detecte un efecto significativo. El panel izquierdo de la Figura 32.2 muestra que cuando la potencia es baja, el tamaño estimado del efecto para resultados significativos puede ser altamente inflado en comparación con el tamaño real del efecto.

Figura 32.2: Izquierda: Una simulación de la maldición del ganador en función del poder estadístico (eje x). La línea continua muestra el tamaño estimado del efecto y la línea punteada muestra el tamaño real del efecto. Derecha: Histograma que muestra tamaños de muestra para un número de muestras de un conjunto de datos, con resultados significativos mostrados en azul y resultados no significativos en rojo.

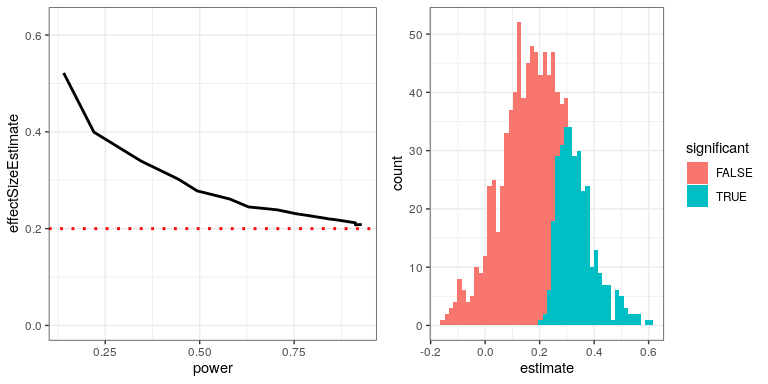
Podemos mirar una sola simulación para ver por qué es así. En el panel derecho de la Figura 32.2, se puede ver un histograma de los tamaños de efecto estimados para 1000 muestras, separados por si la prueba fue estadísticamente significativa. Debe quedar claro a partir de la cifra que si estimamos el tamaño del efecto solo con base en resultados significativos, entonces nuestra estimación se inflará; solo cuando la mayoría de los resultados sean significativos (es decir, la potencia es alta y el efecto es relativamente grande) nuestra estimación se acercará al tamaño real del efecto.