1.3: Eliminación de componentes de tendencia

En esta sección se desarrollan tres métodos diferentes para estimar la tendencia de un modelo de series temporales. Se supone que tiene sentido postular el modelo (1.1.1) con\(s_t=0\) para todos\(t\in T\), es decir,

\[X_t=m_t+Y_t, t\in T \tag{1.3.1} \label{Eq131} \]

donde (sin pérdida de generalidad)\(E[Y_t]=0\). En particular, se discuten tres métodos diferentes, (1) la estimación de mínimos cuadrados de\(m_t\), (2) suavizado por medio de promedios móviles y (3) diferenciación.

Método 1 (Estimación de mínimos cuadrados) A menudo es útil suponer que un componente de tendencia puede ser modelado apropiadamente por un polinomio,

\[ m_t=b_0+b_1t+\ldots+b_pt^p, \qquad p\in\mathbb{N}_0. \nonumber \]

En este caso, los parámetros desconocidos\(b_0,\ldots,b_p\) pueden ser estimados por el método de mínimos cuadrados. Combinados, producen la tendencia polinómica estimada

\[ \hat{m}_t=\hat{b}_0+\hat{b}_1t+\ldots+\hat{b}_pt^p, \qquad t\in T, \nonumber \]

donde\(\hat{b}_0,\ldots,\hat{b}_p\) denotan las estimaciones correspondientes de mínimos cuadrados. Tenga en cuenta que el orden no\(p\) es estimado. Tiene que ser seleccionado por el estadístico, por ejemplo, inspeccionando la trama de series de tiempo. Los residuos\(\hat{Y}_t\) se pueden obtener como

\[ \hat{Y}_t=X_t-\hat{m}_t=X_t-\hat{b}_0-\hat{b}_1t-\ldots-\hat{b}_pt^p, \qquad t\in T. \nonumber \]

La forma de evaluar la bondad de ajuste de la tendencia ajustada será objeto de la Sección 1.5 a continuación.

Ejemplo 1.3.1 (Nivel del Lago Huron). El panel izquierdo de la Figura 1.7 contiene la serie temporal de los niveles de agua promedio anuales en pies (reducidos en 570) del lago Huron de 1875 a 1972. Es una realización del proceso
\ [
x_t=\ mbox {(Nivel promedio de agua del Lago Huron en el año $1874+t$)} -570,
\ qquad t=1,\ ldots,98.
\ nonumber\] Parece
haber una disminución lineal en el nivel del agua y por lo tanto es razonable ajustar un polinomio de orden uno a los datos. Evaluar los estimadores de mínimos cuadrados nos proporciona los valores

\[ \hat{b}_0=10.202 \qquad\mbox{and}\qquad \hat{b}_1=-0.0242 \nonumber \]

para la intercepción y la pendiente, respectivamente. Los residuos observados resultantes\(\hat{y}_t=\hat{Y}_t(\omega)\) se representan frente al tiempo en el panel derecho de la Figura 1.7. No queda tendencia aparente en los datos. Por otro lado, la trama no soporta fuertemente la estacionariedad de los residuos. Adicionalmente, hay evidencia de dependencia en los datos.

Para reproducir el análisis en R, supongamos que los datos están almacenados en el archivo lake.dat. Después usa los siguientes comandos.

> lake = read.table (” lake.dat “)
> lake = ts (lago, start=1875)
> t = 1:longitud (lago)
> lsfit = lm (lake$^\ mathrm {\ sim} $t)
> parcela (t, lago, xlab="”, ylab= "”, principal= "”)
> líneas (lsfit {\ $} ajuste)

La función lm ajusta un modelo lineal o línea de regresión a los datos de Lake Huron. Para trazar tanto el conjunto de datos original como la línea de regresión ajustada en la misma gráfica, primero puede trazar los niveles de agua y luego usar la función lines para superponer el ajuste. Se puede acceder a los residuos correspondientes al ajuste del modelo lineal con el comando lsfit$resid.

\ end {exmp}

Método 2 (Suavizado con Medias Móviles) Dejar\((X_t\colon t\in\mathbb{Z})\) ser un proceso estocástico siguiendo el modelo\(\ref{Eq131}\). Elige\(q\in\mathbb{N}_0\) y define la media móvil de dos lados
\ begin {ecuación}\ label {eq:wt}
w_t=\ frac {1} {2q+1}\ sum_ {j=-q} ^qx_ {t+j},\ qquad t\ in\ mathbb {Z}. \ tag {1.3.2}\ end {equation}
Las variables aleatorias se\(W_t\) pueden utilizar para estimar el componente\(m_t\) de tendencia de la siguiente manera. Primero tenga en cuenta que
\ [
w_t=\ frac {1} {2q+1}\ sum_ {j=-q} ^qm_ {t+j} +\ frac {1} {2q+1}\ sum_ {j=-q} ^qy_ {t+j}\ approx m_t,
\ nonumber\]
asumiendo que la tendencia es localmente aproximadamente lineal y que el promedio de la\(Y_t\) sobreel intervalo\([t-q,t+q]\) es cerca de cero. Por lo tanto, se\(m_t\) puede estimar por

\[ \hat{m}_t=W_t,\qquad t=q+1,\ldots,n-q. \nonumber \]

Observe que no hay posibilidad de estimar el primer\(q\) y último término de\(n-q\) deriva debido a la naturaleza de dos lados de las medias móviles. Por el contrario, también se pueden definir promedios móviles unilaterales dejando

\[ \hat{m}_1=X_1,\qquad \hat{m}_t=aX_t+(1-a)\hat{m}_{t-1},\quad t=2,\ldots,n. \nonumber \]

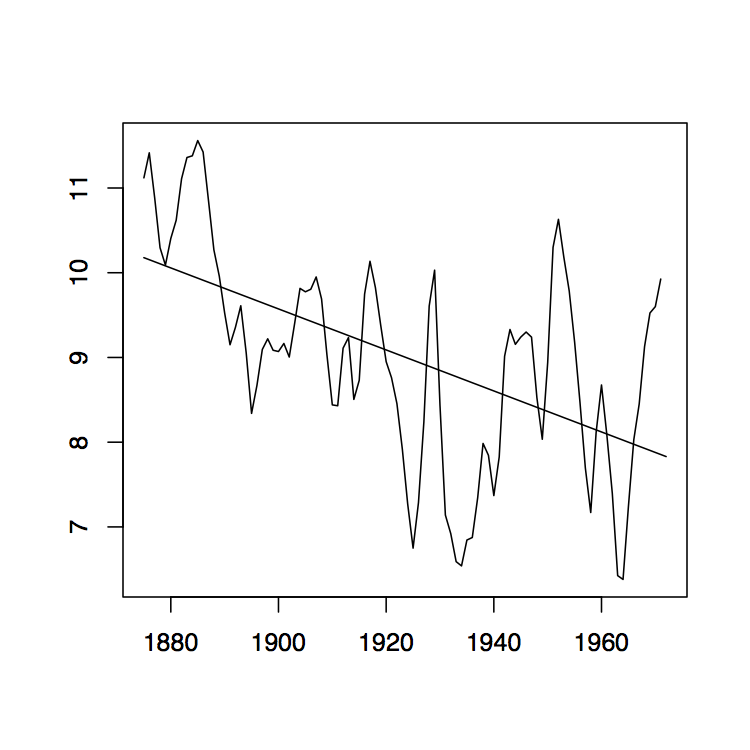
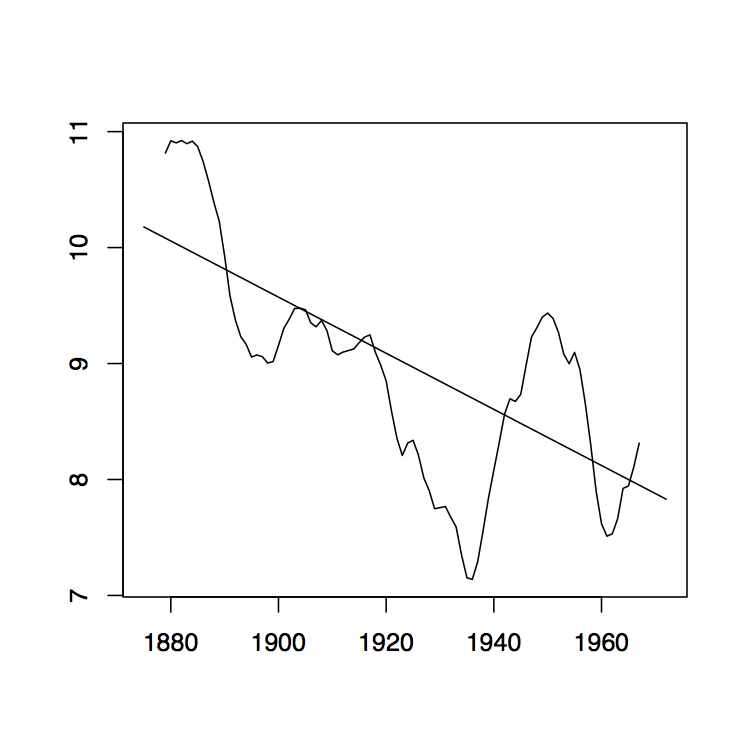
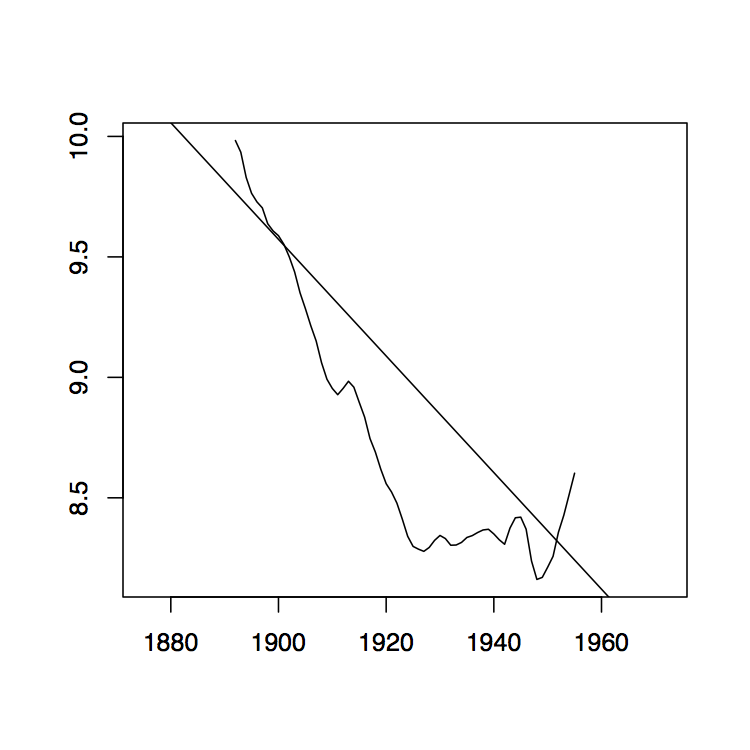
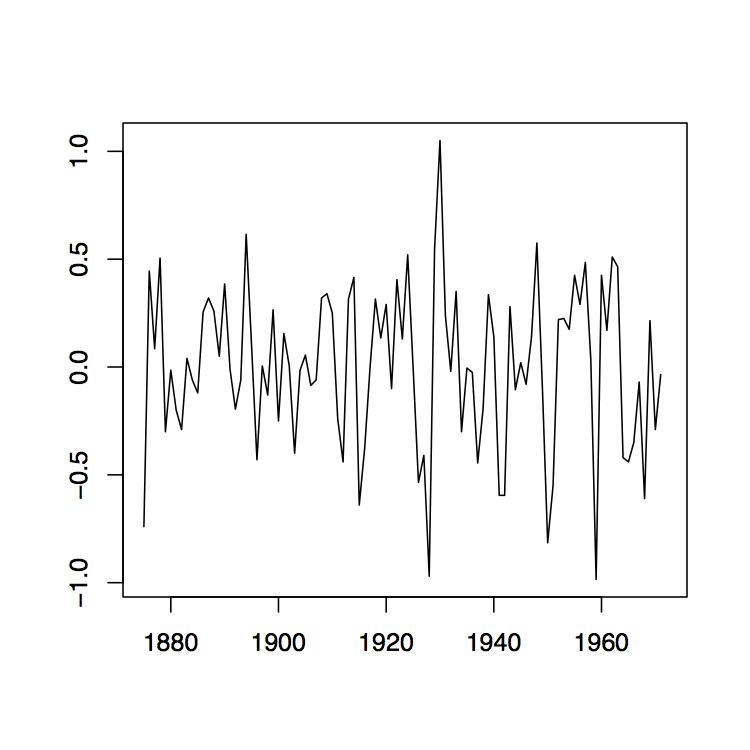
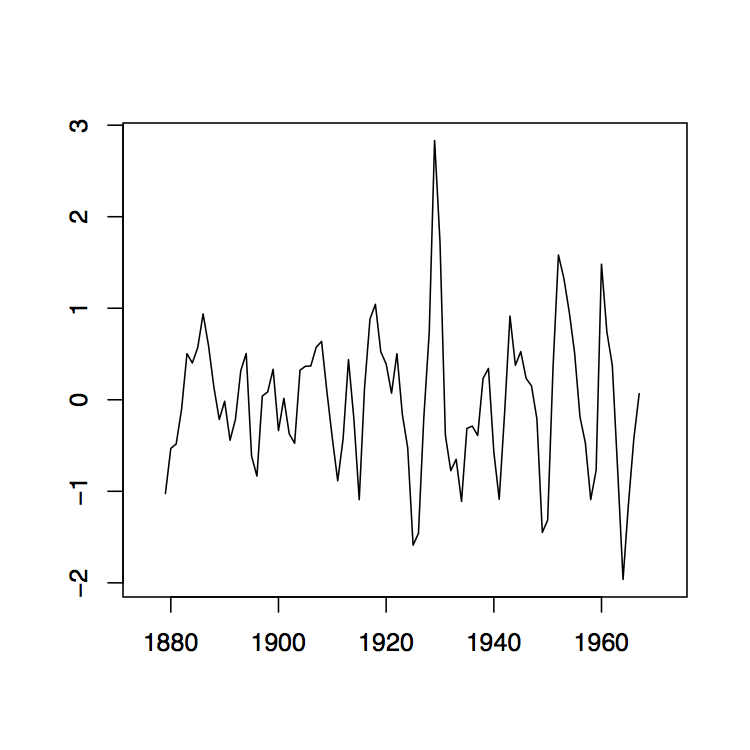
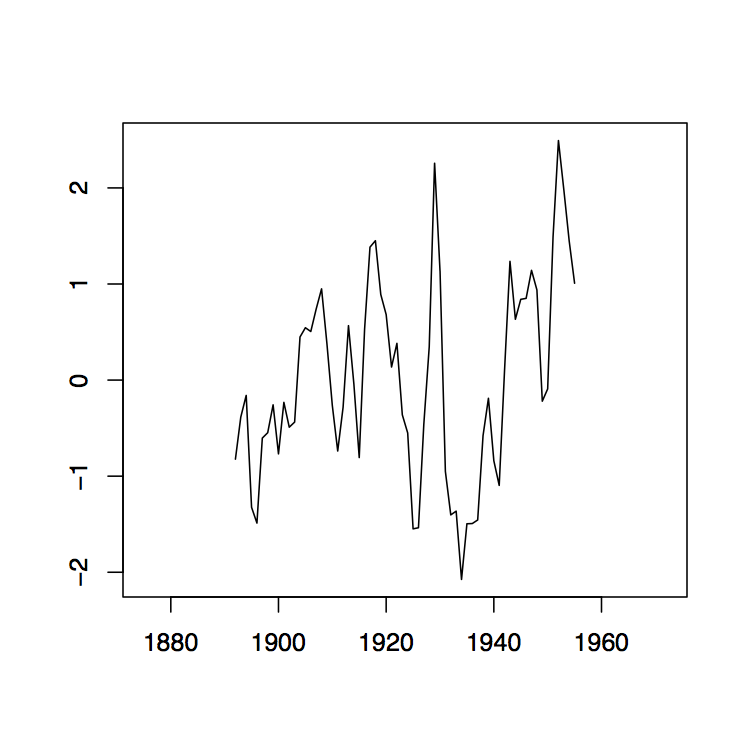
• Figura 1.8: La media móvil de dos lados filtra W t para los datos de Lake Huron (panel superior) y sus residuales (panel inferior) con ancho de banda q = 2 (izquierda), q = 10 (medio) y q = 35 (derecha).

La Figura 1.8 contiene estimadores\(\hat{m}_t\) basados en los promedios móviles de dos lados para los datos de Lake Huron del Ejemplo 1.3.1. para elecciones seleccionadas de\(q\) (panel superior) y los residuales estimados correspondientes (panel inferior).

Los filtros de media móvil para este ejemplo se pueden producir en R de la siguiente manera:

> t = 1:longitud (lago)
> ma2 = filtro (lago, lados=2, rep (1,5) /5)
> ma10 = filtro (lago, lados=2, rep (1,21) /21)
> ma35 = filtro (lago, lados=2, rep (1,71) /71)
> parcela (t, ma2, xlab= "”, ylab= "”, type="l”)
> líneas (t, ma10); líneas (t, ma35)

Allí, los lados determinan si se va a usar un filtro de uno o dos lados. La frase rep (1,5) crea un vector de longitud 5 siendo cada entrada igual a 1.

Se pueden obtener versiones más generales de los suavizadores de media móvil de la siguiente manera. Observe que en el caso de la versión de dos caras\(W_t\) cada variable\(X_{t-q},\ldots,X_{t+q}\) obtiene un “peso”\(a_j=(2q+1)^{-1}\). La suma de todos los pesos es así igual a uno. Lo mismo es cierto para los promedios móviles unilaterales con pesos\(a\) y\(1-a\). Por lo general, uno puede definir un suavizado dejando

\[\hat{m}_t=\sum_{j=-q}^qa_jX_{t+j}, \qquad t=q+1,\ldots,n-q, \tag{1.3.3} \label{Eq133} \]

donde\(a_{-q}+\ldots+a_q=1\). Estos promedios móviles generales (de dos lados y de un lado) se conocen comúnmente como filtros lineales. Hay innumerables opciones para los pesos. El de aquí,\(a_j=(2q+1)^{-1}\), tiene la ventaja de que las tendencias lineales pasan sin distorsiones. En el siguiente ejemplo, se introduce un filtro que pasa tendencias cúbicas sin distorsión.

Ejemplo 1.3.2 (media móvil de 15 puntos de Spencer). Supongamos que el filtro en visualización\(\ref{Eq133}\) está definido por pesos que satisfacen\(a_j=0\) if\(|j|>7\),\(a_j=a_{-j}\) y
\ [
(a_0, a_1,\ ldots, a_7) =\ frac {1} {320} (74,67,46,21,3, -5, -6, -3).
\ nonumber\]
Entonces, los filtros correspondientes pasan tendencias cúbicas\(m_t=b_0+b_1t+b_2t^2+b_3t^3\) sin distorsionar. Para ver esto, observe que
\ begin {align*}
\ sum_ {j=-7} ^7a_j=1\ qquad\ mbox {y}\ qquad
\ sum_ {j=-7} ^7j^ra_j=0,\ qquad r=1,2,3.
\ end {align*}
Ahora aplica la Proposición 1.3.1 a continuación para llegar a la conclusión. Suponiendo que las observaciones están en los datos, utilice los comandos R

> a = c (-3, -6, -5, 3, 21, 46, 67, 74, 67, 46, 21, 3, -5, -6, -3) /320
> s15 = filtro (datos, lados=2, a)

para aplicar el filtro Promedio móvil de 15 puntos de Spencer. Este ejemplo también explica cómo especificar un filtro general hecho a medida para un conjunto de datos dado.

Proposición 1.3.1. Un filtro lineal (1.3.3) pasa un polinomio de grado\(p\) si y solo si
\ [
\ sum_ {j} a_j=1\ qquad\ mbox {y}\ qquad\ sum_ {j} j^ra_j=0,\ qquad r=1,\ ldots, p.
\ nonumber\]
Prueba. Baste demostrar eso\(\sum_ja_j(t+j)^r=t^r\) para\(r=0,\ldots,p\). Usando el teorema binomial, escribe
\ begin {align*}
\ sum_ja_j (t+j) ^r
&=\ sum_ja_j\ sum_ {k=0} ^r {r\ elige k} t^kj^ {r-k}\\ [.2cm]
&=\ suma_ {k=0} ^r {r\ elige k} t^k\ left (\ sum_ja_jj^ {r-k}\ derecha)\\ [.2cm]
&=t^r
\ end {align *}
para cualquiera\(r=0,\ldots,p\) si y solo si las condiciones anteriores se mantienen.

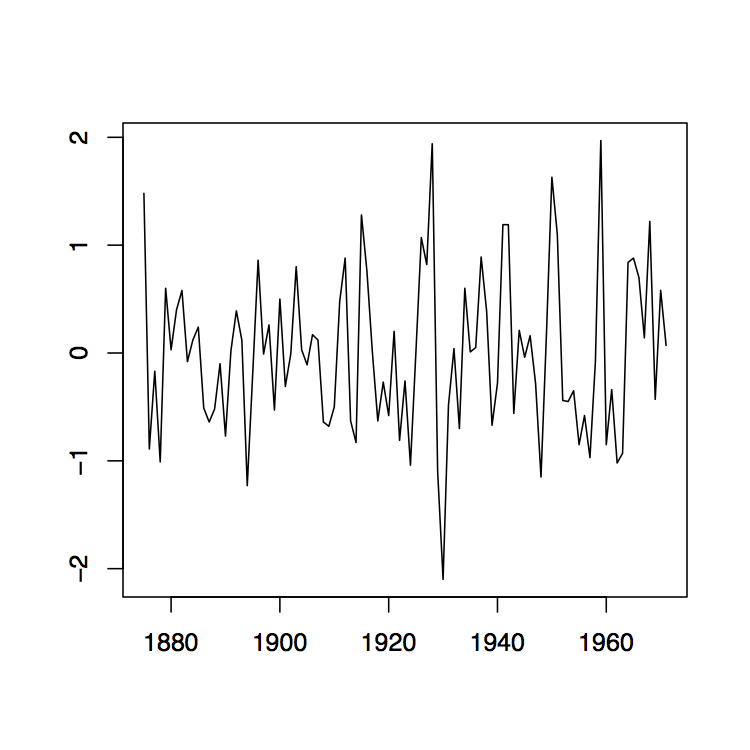
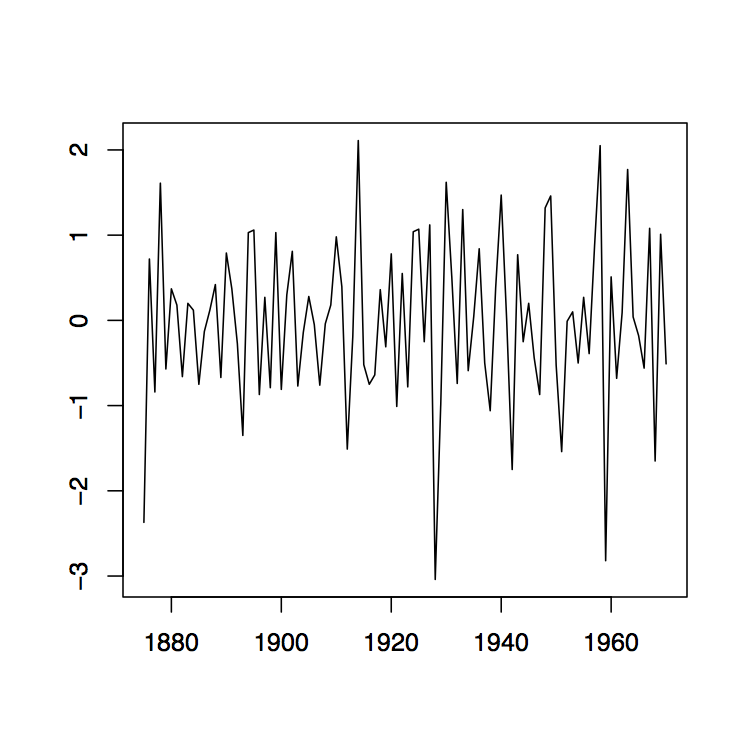
• Figura 1.9: Gráficas de series temporales de las secuencias observadas (x t) en el panel izquierdo y (2 x t) en el panel derecho del diferenciaron los datos de Lake Huron descritos en el Ejemplo 1.3.1.

Método 3 (Diferenciación) Una tercera posibilidad para eliminar términos de deriva de una serie de tiempo dada es la diferenciación. Para ello, introduce el operador de diferencia\(\nabla\) como
\ [
\ nabla x_t=x_t-x_ {t-1} =( 1-B) x_t,\ qquad t\ in T,
\ nonumber\]
donde\(B\) denota el operador de retroceso\(BX_t=X_{t-1}\). La aplicación repetida de\(\nabla\) se define de la manera intuitiva:

\ [\ nABLA^2x_t=\ nabla (\ nabla x_t) =\ nabla (x_t-x_ {t-1}) =x_t-2x_ {t-1} +X_ {t-2}
\ nonumber\]
y, recursivamente, las representaciones siguen también para potencias superiores de\(\nabla\). Supongamos que el operador diferencia se aplica a la tendencia lineal\(m_t=b_0+b_1t\), entonces

\ [\ nabla m_t=m_t-m_ {t-1} =b_0+b_1t-b_0-b_1 (t-1) =b_1
\ nonumber\]
que es una constante. Inductivamente, esto lleva a la conclusión de que para un polinomio deriva de grado\(p\), es decir\(m_t=\sum_{j=0}^pb_jt^j\),\(\nabla^pm_t=p!b_p\) y por lo tanto constante. Aplicando esta técnica a un proceso estocástico de la forma (1.3.1) con una deriva polinómica\(m_t\), produce entonces
\ [
\ nAbla^px_t=P! b_p+\ nabla^p y_T,\ qquad t\ in T.
\ nonumber\]
Este es un proceso estacionario con media\(p!b_p\). Las gráficas de la Figura 1.9 contienen las diferencias primera y segunda para los datos de Lake Huron. En R, se pueden obtener de los comandos

> d1 = diff (lago)
> d2 = diff (d1)
> par (mfrow=c (1,2))
> plot.ts (d1, xlab= "”, ylab= "”)
> plot.ts (d2, xlab= "”, ylab= "”)

El siguiente ejemplo muestra que el operador de diferencia también se puede aplicar a una caminata aleatoria para crear datos estacionarios.

Ejemplo 1.3.3. Dejar\((S_t\colon t\in\mathbb{N}_0)\) ser el paseo aleatorio del Ejemplo 1.2.3. Si el operador diferencia\(\nabla\) se aplica a este proceso estocástico, entonces
\ [
\ nabla s_t=s_t-s_ {t-1} =z_t,\ qquad t\ in\ mathbb {N}.
\ nonumber\]
En otras palabras,\(\nabla\) no hace otra cosa que recuperar la secuencia original de ruido blanco que se utilizó para construir la caminata aleatoria.