1.4: Eliminación de componentes de tendencia y estacionales

Recordemos la descomposición clásica (1.1.1),
\ [
x_t=m_t+s_t+y_t,\ qquad t\ in T,
\ nonumber\]
con\(E[Y_t]=0\). En esta sección se discuten tres métodos que tienen como objetivo estimar tanto la tendencia como los componentes estacionales en los datos. Como requisito adicional on\((s_t\colon t\in T)\), se asume que
\ [
s_ {t+d} =s_t,\ qquad\ sum_ {j=1} ^ds_j=0,
\ nonumber\]
donde\(d\) denota el periodo del componente estacional. (Si se trata de datos anuales muestreados mensualmente, entonces obviamente\(d=12\).) Es conveniente remarcar las observaciones\(x_1,\ldots,x_n\) en términos del periodo estacional\(d\) como
\ [x_ {j, k} =x_ {k+d (j-1)}.
\ nonumber\]
En el caso de los datos anuales, la observación representa\(x_{j,k}\) así el punto de datos observado para el mes\(k\) th del año\(j\) th. Por conveniencia siempre se hace referencia a los datos de esta manera aunque el periodo real sea algo distinto al 12.

Método 1 (Método de tendencia pequeña) Si los cambios en el término deriva parecen ser pequeños, entonces es razonable suponer que la deriva en el año\(j\), digamos,\(m_j\) es constante. Por lo tanto, como estimador natural se puede aplicar
\ [
\ hat {m} _j=\ frac {1} {d}\ sum_ {k=1} ^dx_ {j, k}.
\ nonumber\]
Para estimar la estacionalidad en los datos, uno puede en un segundo paso utilizar las cantidades
\ [
\ hat {s} _k=\ frac 1N\ sum_ {j=1} ^N (x_ {j, k} -\ hat {m} _j),
\ nonumber\]
donde\(N\) se determina por el \(n=Nd\), siempre que los datos hayan sido recolectados a lo largo de ciclos\(N\) completos. Los cálculos directos muestran que estos estimadores poseen la propiedad\(\hat{s}_1+\ldots+\hat{s}_d=0\) (como en el caso de los verdaderos componentes estacionales\(s_t\)). Para evaluar aún más la calidad del ajuste, es necesario analizar los residuales observados
\ [
\ hat {y} _ {j, k} =x_ {j, k} -\ hat {m} _j-\ hat {s} _k.
\ nonumber\]
Obsérvese que debido al remarcaje de las observaciones y al supuesto de una tendencia que cambia lentamente, el el componente de deriva se describe únicamente por el subíndice “anual”\(j\), mientras que el componente estacional solo contiene el subíndice “mensual”\(k\).

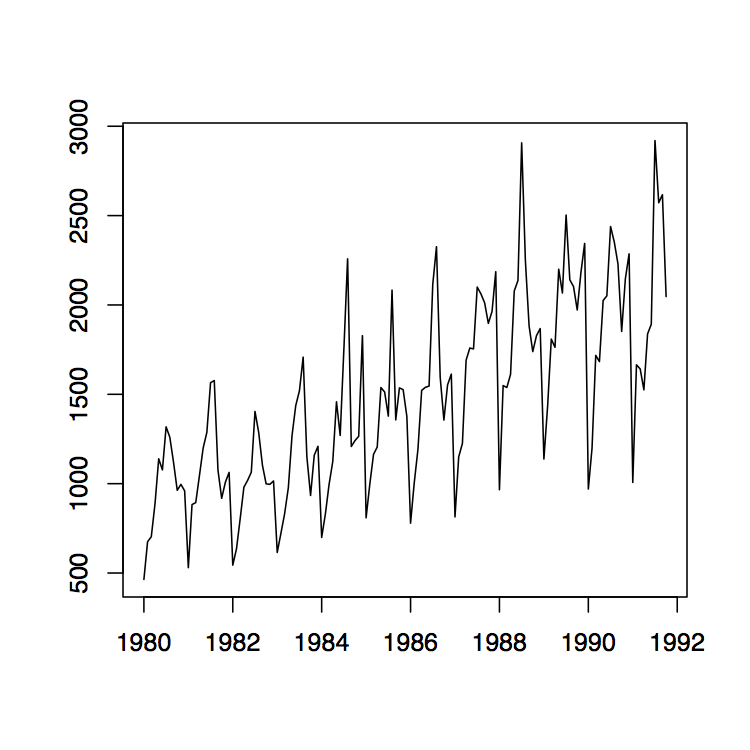
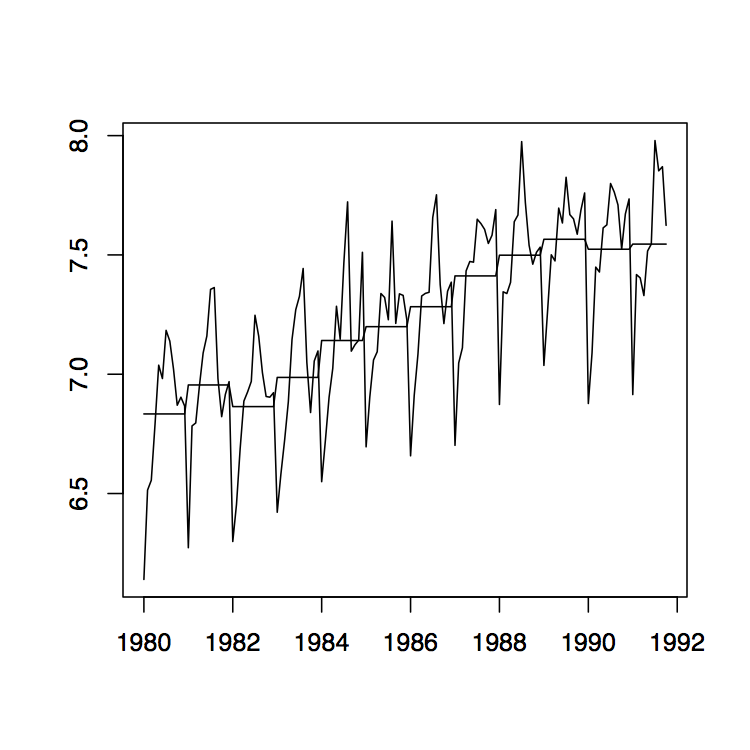
• Figura 1.10: Parcelas de series temporales de las ventas de vino tinto en Australia de enero de 1980 a octubre de 1991 (izquierda) y su transformación logarítmica con estimaciones medias anuales (derecha).

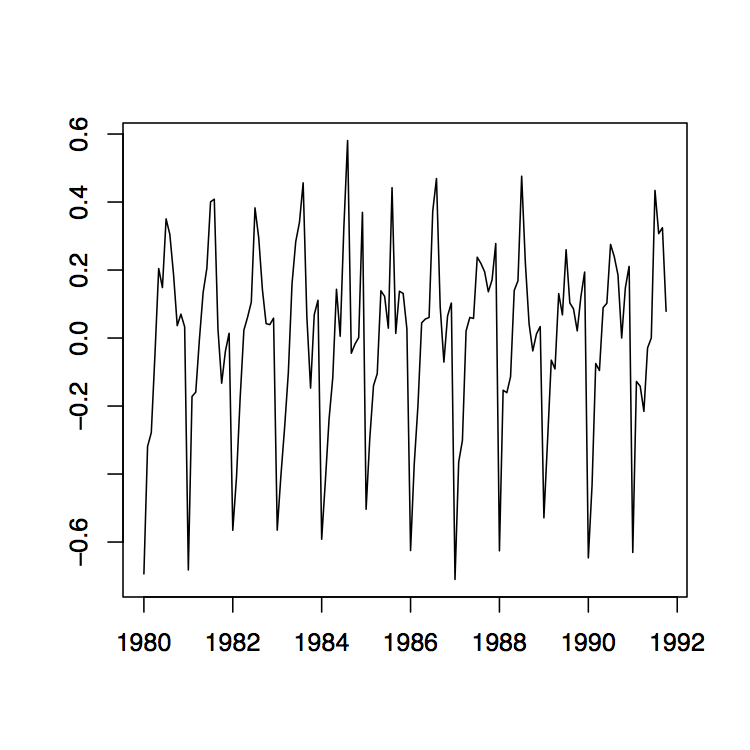
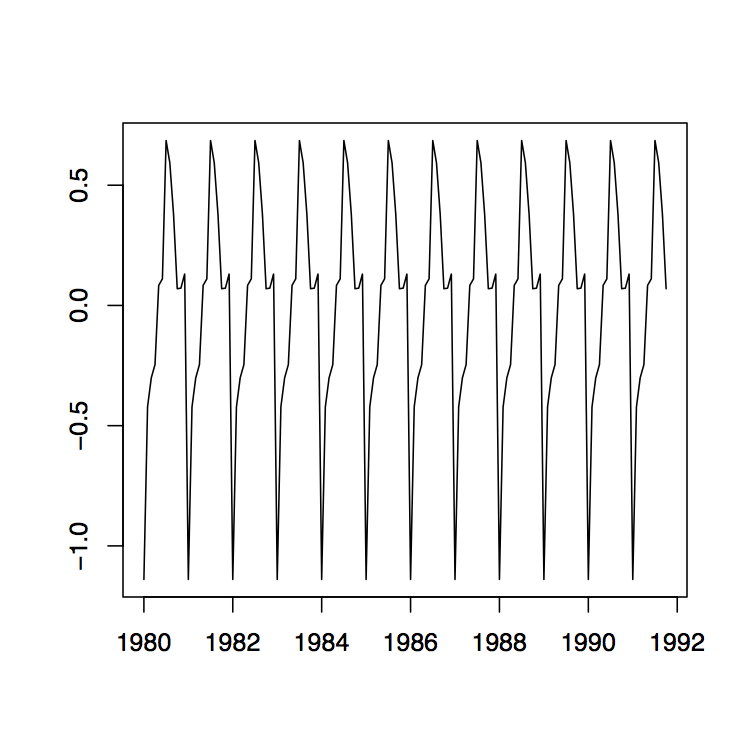
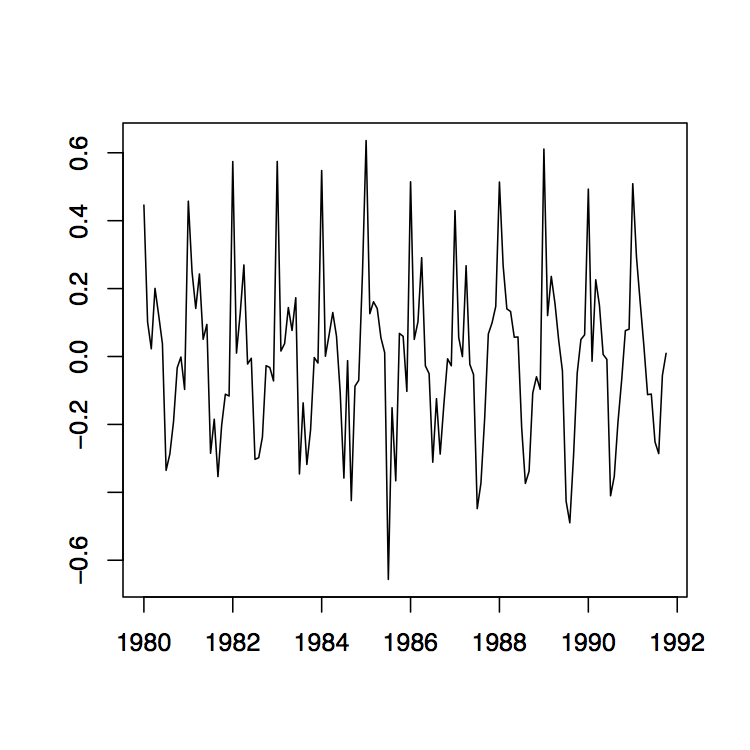
Ejemplo 1.4.1 (Ventas de Vino Australiano). El panel izquierdo de la Figura 1.10 muestra las ventas mensuales de vino tinto (en kilolitros) en Australia de enero de 1980 a octubre de 1991. Dado que hay un aumento aparente en las fluctuaciones a lo largo del tiempo, el panel derecho de la misma figura muestra la transformación logaritmo natural de los datos. Existe evidencia clara tanto de tendencia como de estacionalidad. A continuación se estudian los datos transformados logarítmicos. Utilizando el método de tendencia pequeña como se describió anteriormente, se estiman primero las medias anuales. Ya están incorporadas en la gráfica de serie temporal correcta de la Figura 1.10. Obsérvese que sólo hay diez meses de datos disponibles para el año 1991, por lo que la estimación tiene que ajustarse en consecuencia. Los datos detendenciados se muestran en el panel izquierdo de la Figura 1.11. La gráfica media en la misma figura muestra el componente estacional estimado, mientras que el panel derecho muestra los residuos. A pesar de que la suposición de pequeños cambios en la deriva es algo cuestionable, los residuos parecen verse bastante bonitos. Indican que hay dependencia en los datos (ver Sección 1.5 a continuación para más información sobre este tema).

• Figura 1.11: La serie logarítmica detendida (izquierda), el componente estacional estimado (centro) y las series residuales correspondientes (derecha) de los datos de ventas de vino tinto australiano.

Método 2 (Estimación de media móvil) Este método debe preferirse sobre el primero siempre que el componente de tendencia subyacente no pueda asumirse constante. Se van a aplicar tres pasos a los datos.

1er Paso: Estimación de tendencia. Al principio, enfocarse en la eliminación del componente de tendencia con los filtros lineales discutidos en la sección anterior. Si el periodo\(d\) es impar, entonces uno puede usar directamente\(\hat{m}_t=W_t\) como en (1.3.2) con\(q\) especificado por la ecuación\(d=2q+1\). Si el periodo\(d=2q\) es par, entonces modifica ligeramente\(W_t\) y usa
\ [
\ hat {m} _t=\ frac 1d (.5x_ {t-q} +x_ {t-q+1} +\ ldots+x_ {t+q-1} +.5x_ {t+q}),
\ qquad t=q+1,\ ldots, n-q.
\ nonumber\]

2do Paso: Estimación de estacionalidad. Para estimar el componente estacional, vamos
\ begin {align*}
\ mu_k&=\ frac 1 {N-1}\ sum_ {j=2} ^N (x_ {k+d (j-1)} -\ hat {m} _ {k+d (j-1)}),
\ qquad k=1,\ ldots, q,\\ [.2cm]
\ mu_k&=\ ac 1 {N-1}\ suma_ {j=1} ^ {N-1} (x_ {k+d (j-1)} -\ hat {m} _ _ {k+d (j-1)}),
\ qquad k=q+1,\ ldots, d.
\ end {align*}
Definir ahora
\ [
\ hat {s} _k=\ mu_k-\ frac 1d\ sum_ {\ ell=1} ^d\ mu_\ ell,\ qquad k=1,\ ldots, d,
\ nonumber\]
y establecer\(\hat{s}_{k}=\hat{s}_{k-d}\) siempre\(k>d\). Esto nos proporcionará datos desestacionalizados que pueden ser examinados más a fondo. En el paso final, cualquier tendencia restante se puede eliminar de los datos.

3er Paso: Reestimación de Tendencia. Aplicar cualquiera de los métodos de la Sección 1.3.

Método 3 (Diferenciación al lag d) Introduciendo el operador de diferencia lag-d\(\nabla_d\), definido dejando

\ [\ nAbla_dx_t=x_t-x_ {t-d} =( 1-b^d) x_t,\ qquad t=d+1,\ ldots, n,
\ nonumber\]
y asumiendo el modelo (1.1.1), uno llega a las variables aleatorias transformadas

\ [\ nAbla_dx_t=m_t-m_ {t-d} +Y_t-y_ {t-d},\ qquad t=d+1,\ ldots, n.
\ nonumber\]
Tenga en cuenta que se elimina la estacionalidad, ya que\(s_t=s_{t-d}\). Las variables de ruido restantes\(Y_t-Y_{t-d}\) son estacionarias y tienen media cero. El nuevo componente de tendencia\(m_t-m_{t-d}\) puede eliminarse utilizando cualquiera de los métodos desarrollados en la Sección 1.3.

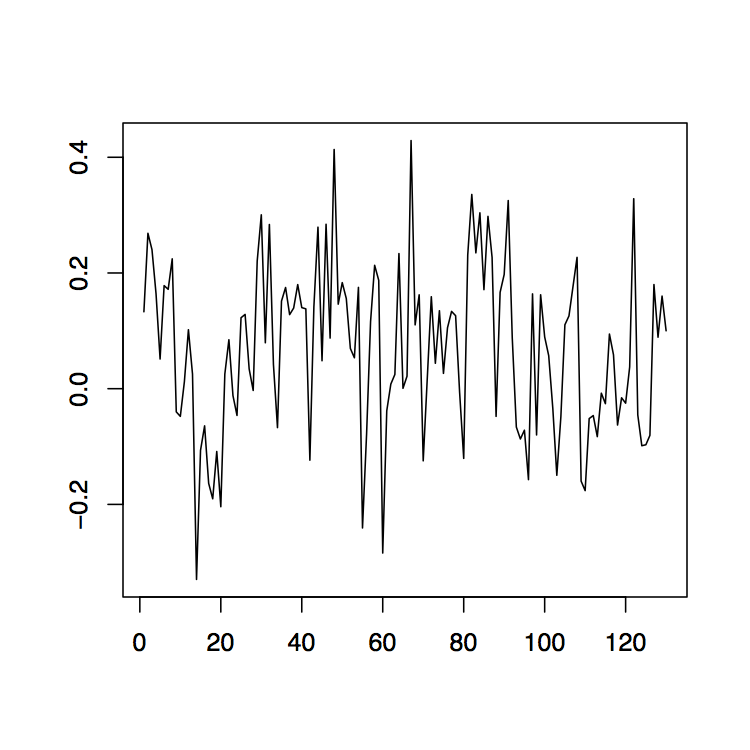
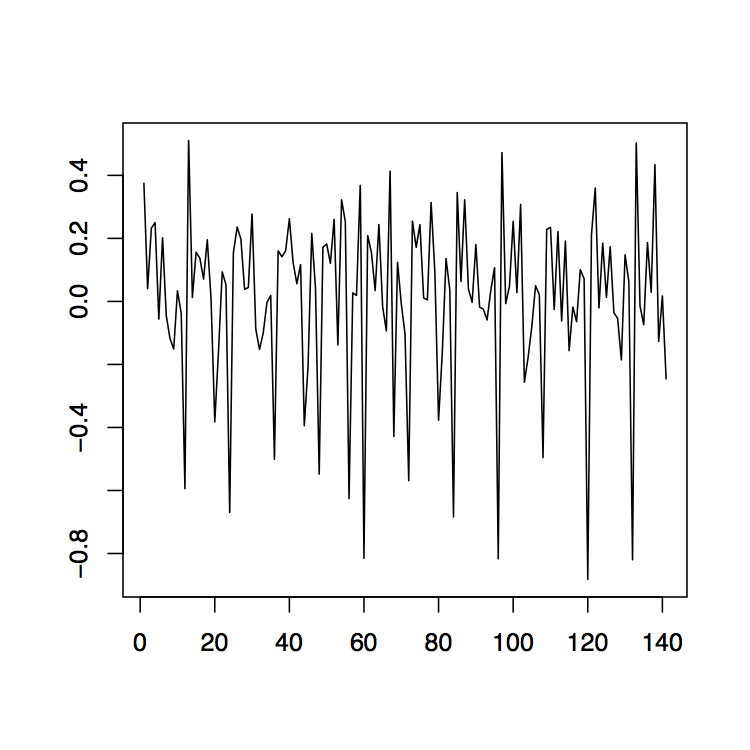
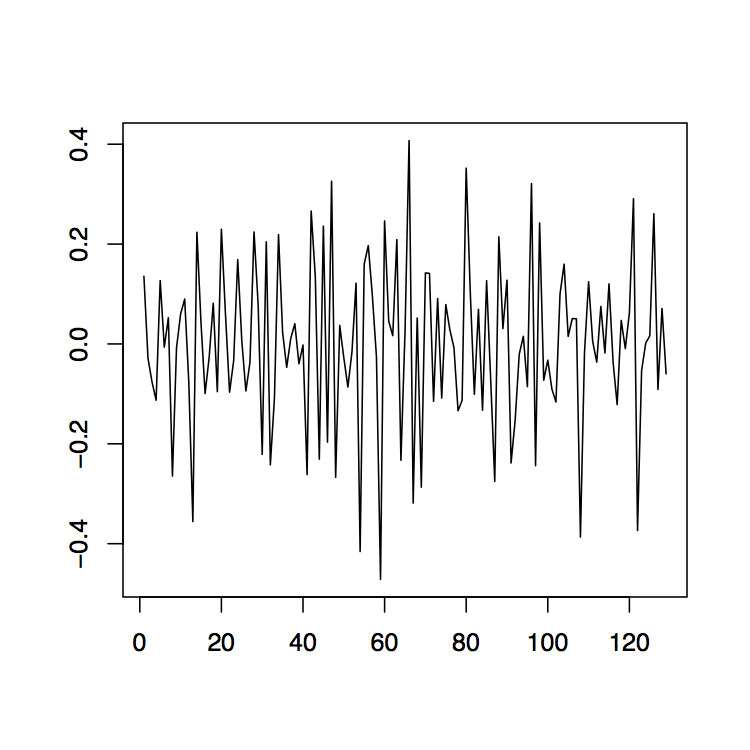
• Figura 1.12: Las series observadas diferenciadas\(\nabla_{12}x_t\) (izquierda),\(\nabla x_t\) (media) y\(\nabla\nabla_{12}x_t=\nabla_{12}\nabla x_t\) (derecha) para los datos de ventas de vino tinto australiano.

Ejemplo 1.4.2 (Ventas de vino australiano). Vuelva a visitar los datos de ventas de vino tinto australiano del Ejemplo 1.4.1 y aplique las técnicas de diferenciación recién establecidas. La gráfica izquierda de la Figura 1.12 muestra los datos después de una aplicación del operador\(\nabla_{12}\). Si la tendencia restante en los datos se estima con el método de diferenciación de la Sección 1.3, se obtiene la gráfica residual dada en el panel derecho de la Figura 1.12. Obsérvese que el orden de aplicación no cambia los residuales, es decir,\(\nabla\nabla_{12}x_t=\nabla_{12}\nabla x_t\). El panel central de la Figura 1.12 muestra los datos diferenciados que aún contienen el componente estacional.