3.3: Distribuciones Mixtas

\(\renewcommand{\P}{\mathbb{P}}\)\(\newcommand{\R}{\mathbb{R}}\)\(\newcommand{\N}{\mathbb{N}}\)

En las dos secciones anteriores, se estudiaron los meausres de probabilidad discretos y las medidas de probabilidad continuas. En esta sección, estudiaremos la medida de probabilidad que sean combinaciones de los dos tipos. Una vez más, si eres un nuevo estudiante de probabilidad es posible que quieras saltarte los detalles técnicos.

Teoría Básica

Definiciones y Propiedades Básicas

Nuestro punto de partida es un experimento aleatorio modelado por un espacio de probabilidad\((S, \mathscr S, \P)\). Entonces, para revisar,\(S\) es el conjunto de resultados,\(\mathscr S\) la recolección de eventos, y\(\P\) la medida de probabilidad en el espacio muestral\((S, \mathscr S)\). Utilizamos los términos medida de probabilidad y distribución de probabilidad como sinónimos en este texto. Además, dado que usamos una definición general de variable aleatoria, cada medida de probabilidad puede ser pensada como la distribución de probabilidad de una variable aleatoria, por lo que siempre podemos tomar este punto de vista si queremos. De hecho, la mayoría de las medidas de probabilidad tienen naturalmente variables aleatorias asociadas a ellas. Aquí está la definición principal:

La medida de probabilidad\(\P\) es de tipo mixto si se\(S\) puede dividir en eventos\(D\) y\(C\) con las siguientes propiedades:

1. \(D\)es contable,\(0 \lt \P(D) \lt 1\) y\(\P(\{x\}) \gt 0\) para cada\(x \in D\).
2. \( C \subseteq \R^n \)para algunos\( n \in \N_+ \) y\(\P(\{x\}) = 0\) para cada uno\(x \in C\).

Detalles

Recordemos que el término partición significa que\(D\) y\(C\) son disjuntos y\(S = D \cup C\). Como siempre,\(\mathscr S\) se requiere que la colección de eventos sea un\(\sigma\) álgebra. El conjunto\( C \) es un subconjunto medible de\( \R^n \) y luego los elementos de\( \mathscr S \) tienen la forma\( A \cup B \) donde\( A \subseteq D \) y\( B \) es un subconjunto medible de\( C \). Típicamente en aplicaciones,\( C \) se define por un número finito de desigualdades que involucran funciones elementales.

A menudo, el conjunto discreto\(D\) es un subconjunto de\(\R^n\) también, pero eso no es un requisito. Tenga en cuenta que desde\(D\) y\(C\) son complementos,\(0 \lt \P(C) \lt 1\) también. Así, parte de la distribución se concentra en puntos en un conjunto discreto\(D\); el resto de la distribución se extiende continuamente\(C\). En la imagen de abajo, el sombreado azul claro pretende representar una distribución continua de probabilidad mientras que los puntos azules más oscuros están destinados a representar puntos de probabilidad positiva.

Figura\(\PageIndex{1}\): Una distribución mixta en\( S \)

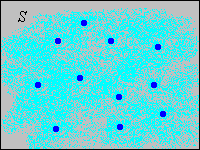
El siguiente resultado es esencialmente equivalente a la definición.

Supongamos que\(\P\) es una medida\(S\) de probabilidad on de tipo mixto como en (1).

1. La medida de probabilidad condicional\(A \mapsto \P(A \mid D) = \P(A) / P(D)\) para\(A \subseteq D\) es una distribución discreta en\(D\)
2. La medida de probabilidad condicional\(A \mapsto \P(A \mid C) = \P(A) / \P(C)\) para\(A \subseteq C\) es una distribución continua en\(C\).

Prueba

En general, las medidas de probabilidad condicional son realmente medidas de probabilidad, por lo que los resultados son obvios ya que\(\P(\{x\} \mid D) \gt 0\) para\(x\) en el conjunto contable\(D\), y\(\P(\{x\} \mid C) = 0\) para\(x \in C\). Desde otro punto de vista,\(\P\) restringidos a subconjuntos\(D\) y\(\P\) restringidos a subconjuntos de\(C\) son medidas finitas y por lo tanto se pueden normalizar para producir medidas de probabilidad.

Tenga en cuenta que\[\P(A) = \P(D) \P(A \mid D) + \P(C) \P(A \mid C), \quad A \in \mathscr S\] Así, la medida de probabilidad\(P\) realmente es una mezcla de una distribución discreta y una distribución continua. Las mezclas se estudian en mayor generalidad en la sección sobre distribuciones condicionales. Podemos definir una función sobre\(D\) esa es una función de densidad de probabilidad parcial para la parte discreta de la distribución.

Supongamos que\(\P\) es una medida\(S\) de probabilidad on de tipo mixto como en (1). Dejar\(g\) ser la función definida por\(g(x) = \P(\{x\})\) for\(x \in D\). Entonces

1. \(g(x) \ge 0\)para\(x \in D\)
2. \(\sum_{x \in D} g(x) = \P(D)\)
3. \(\P(A) = \sum_{x \in A} g(x)\)para\(A \subseteq D\)

Prueba

Estos resultados se derivan de los axiomas de probabilidad.

1. \(g(x) = \P(\{x\}) \ge 0\)ya que las probabilidades no son negativas.
2. \(\sum_{x \in D} g(x) = \sum_{x \in D} \P(\{x\}) = \P(D)\)por aditividad contable.
3. \(\sum_{x \in A} g(x) = \sum_{x \in A} \P(\{x\}) = \P(A)\)pues\(A \subseteq D\), de nuevo por aditividad contable.

Técnicamente,\(g\) es una función de densidad con respecto a contar la medida\(\#\)\(D\), la medida estándar utilizada para espacios discretos.

Claramente, la función normalizada\(x \mapsto g(x) / \P(D)\) es la función de densidad de probabilidad de la distribución condicional dada\(D\), discutida en (2). A menudo, la parte continua de la distribución también se describe mediante una función de densidad de probabilidad parcial.

Una función de densidad de probabilidad parcial para la parte continua de\(\P\) es una función no negativa\(h: C \to [0, \infty)\) tal que\[ \P(A) = \int_A h(x) \, dx, \quad A \in \mathscr C \]

Detalles

Técnicamente,\(h\) se requiere que sea medible, y es una función de densidad con respecto a la medida de Lebesgue\(\lambda_n\) en\(C\), la medida estándar en\(\R^n\).

Claramente, la función normalizada\(x \mapsto h(x) / \P(C)\) es la función de densidad de probabilidad de la distribución condicional dada\(C\) discutida en (2). Al igual que con las distribuciones puramente continuas, no se garantiza la existencia de una función de densidad de probabilidad para la parte continua de una distribución mixta. Y cuando existe, una función de densidad para la parte continua no es única. Tenga en cuenta que los valores de\( h \) podrían cambiarse a otros valores no negativos en un subconjunto contable de\(C\), y la ecuación mostrada arriba aún se mantendría, porque solo las integrales de\( h \) son importantes. La medida de probabilidad\(\P\) está completamente determinada por las funciones de densidad de probabilidad parcial.

Supongamos que\(\P\) tiene funciones de densidad de probabilidad parcial\(g\) y\(h\) para las partes discretas y continuas, respectivamente. Entonces\[ \P(A) = \sum_{x \in A \cap D} g(x) + \int_{A \cap C} h(x) \, dx, \quad A \in \mathscr S \]

Prueba

Figura\(\PageIndex{2}\): Una distribución mixta está completamente determinada por sus funciones de densidad parcial.

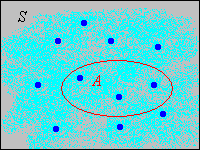
Variables truncadas

Las distribuciones de tipo mixto ocurren naturalmente cuando una variable aleatoria con una distribución continua se trunca de cierta manera. Por ejemplo, supongamos que\(T\) es la vida al azar de un dispositivo, y tiene una distribución continua con función de densidad de probabilidad\(f\) que es positiva en\([0, \infty)\). En una prueba del dispositivo, no podemos esperar para siempre, así que podríamos seleccionar una constante positiva\(a\) y registrar la variable aleatoria\(U\), definida truncando\(T\) en\(a\), de la siguiente manera:\[ U = \begin{cases} T, & T \lt a \\ a, & T \ge a \end{cases}\]

\(U\)tiene una distribución mixta. En la notación anterior,

1. \(D = \{a\}\)y\(g(a) = \int_a^\infty f(t) \, dt\)
2. \(C = [0, a)\)y\(h(t)= f(t)\) para\(t \in [0, a)\)

Supongamos siguiente que la variable aleatoria\(X\) tiene una distribución continua encendida\(\R\), con la función de densidad de probabilidad\(f\) que es positiva en\(\R\). Supongamos también que\(a, \, b \in \R\) con\(a \lt b\). La variable se trunca en el intervalo\([a, b]\) para crear una nueva variable aleatoria de la\(Y\) siguiente manera:\[ Y = \begin{cases} a, & X \le a \\ X, & a \lt X \lt b \\ b, & X \ge b \end{cases} \]

\(Y\)tiene una distribución mixta. En la notación anterior,

1. \(D = \{a, b\}\),\(g(a) = \int_{-\infty}^a f(x) \, dx\),\(g(b) = \int_b^\infty f(x) \, dx\)
2. \(C = (a, b)\)y\(h(x) = f(x)\) para\(x \in (a, b)\)

Otra forma en que puede ocurrir una distribución de probabilidad mixta es cuando tenemos un par de variables aleatorias\( (X, Y) \) para nuestro experimento, una con una distribución discreta y la otra con una distribución continua. Este escenario se explora en la siguiente sección sobre Distribuciones Conjuntas.

Ejemplos y Aplicaciones

Supongamos que\(X\) tiene probabilidad\(\frac{1}{2}\) uniformemente distribuida en el conjunto\(\{1, 2, \ldots, 8\}\) y tiene probabilidad\(\frac{1}{2}\) uniformemente distribuida en el intervalo\([0, 10]\). Encuentra\(\P(X \gt 6)\).

Contestar

\(\frac{13}{40}\)

Supongamos que\((X, Y)\) tiene probabilidad\(\frac{1}{3}\) uniformemente distribuida en\(\{0, 1, 2\}^2\) y tiene probabilidad\(\frac{2}{3}\) uniformemente distribuida en\([0, 2]^2\). Encuentra\(\P(Y \gt X)\).

Contestar

\(\frac{4}{9}\)

Supongamos que la vida útil\(T\) de un dispositivo (en unidades de 1000 horas) tiene la distribución exponencial con función de densidad de probabilidad\(f(t) = e^{-t}\) para\(0 \le t \lt \infty\). Una prueba del dispositivo se termina después de 2000 horas;\(U\) se registra la vida útil truncada. Encuentra cada uno de los siguientes:

1. \(\P(U \lt 1)\)
2. \(\P(U = 2)\)

Contestar

1. \(1 - e^{-1} \approx 0.6321\)
2. \(e^{-2} \approx 0.1353\)