1.1: Simulación de Probabilidades Discretas

Probabilidad

En este capítulo, primero consideraremos experimentos fortuitos con un número finito de posibles resultados\(\omega_1\),\(\omega_2\),...,\(\omega_n\). Por ejemplo, rodamos un dado y los posibles resultados son 1, 2, 3, 4, 5, 6 correspondientes al lado que aparece. Lanzamos una moneda con posibles resultados H (cabezas) y T (colas).

Frecuentemente es útil poder referirse a un resultado de un experimento. Por ejemplo, podríamos querer escribir la expresión matemática que da la suma de cuatro rollos de un dado. Para ello, podríamos dejar\(X_i\),\(i = 1, 2, 3, 4,\) representar los valores de los resultados de los cuatro rollos, y luego podríamos escribir la expresión\[X_1 + X_2 + X_3 + X_4\] para la suma de los cuatro rollos. Se llaman los\(X_i\)'s. Una variable aleatoria es simplemente una expresión cuyo valor es el resultado de un experimento en particular. Al igual que en el caso de otros tipos de variables en matemáticas, las variables aleatorias pueden tomar diferentes valores.

\(X\)Sea la variable aleatoria que representa el rollo de un dado. Asignaremos probabilidades a los posibles resultados de este experimento. Hacemos esto asignando a cada resultado\(\omega_j\) un número no negativo de tal\(m(\omega_j)\) manera que\[m(\omega_1) + m(\omega_2) + \cdots + m(\omega_6) = 1\ .\] La función\(m(\omega_j)\) se llame la de la variable aleatoria\(X\). Para el caso del rollo del dado asignaríamos iguales probabilidades o probabilidades 1/6 a cada uno de los resultados. Con esta asignación de probabilidades, se podría escribir\[P(X \le 4) = {2\over 3}\] para significar que la probabilidad es\(2/3\) que un rollo de un dado tenga un valor que no exceda de 4.

\(Y\)Sea la variable aleatoria que representa el lanzamiento de una moneda. En este caso, hay dos posibles resultados, que podemos etiquetar como H y T. A menos que tengamos razones para sospechar que la moneda sale de una manera más a menudo que de otra manera, es natural asignar la probabilidad de 1/2 a cada uno de los dos resultados.

En ambos experimentos anteriores, a cada resultado se le asigna una probabilidad igual. Este ciertamente no sería el caso en general. Por ejemplo, si se encuentra que un medicamento es efectivo el 30 por ciento del tiempo que se usa, podríamos asignar una probabilidad .3 de que el medicamento sea efectivo la próxima vez que se use y .7 que no sea efectivo. Este último ejemplo ilustra lo intuitivo Es decir, si tenemos una probabilidad de\(p\) que un experimento resulte en resultado\(A\), entonces si repetimos este experimento una gran cantidad de veces deberíamos esperar que la fracción de veces que\(A\) ocurrirá sea aproximadamente\(p\). Para comprobar ideas intuitivas como esta, nos resultará útil observar algunos de estos problemas experimentalmente. Podríamos, por ejemplo, lanzar una moneda un gran número de veces y ver si la fracción de veces que las cabezas aparecen es de aproximadamente 1/2. También podríamos simular este experimento en una computadora.

Simulación

Queremos poder realizar un experimento que corresponda a un conjunto dado de probabilidades; por ejemplo,,\(m(\omega_1) = 1/2\)\(m(\omega_2) = 1/3\), y\(m(\omega_3) = 1/6\). En este caso, se podrían marcar tres caras de una matriz de seis caras con una\(\omega_1\), dos caras con una\(\omega_2\), y una cara con una\(\omega_3\).

En el caso general suponemos que\(m(\omega_1)\),\(m(\omega_2)\),...,\(m(\omega_n)\) son todos números racionales, con mínimo denominador común\(n\). Si\(n > 2\), podemos imaginar un troquel cilíndrico largo con una sección transversal que es un\(n\) -gon regular. Si\(m(\omega_j) = n_j/n\), entonces podemos etiquetar\(n_j\) de las caras largas del cilindro con una\(\omega_j\), y si aparece una de las caras finales, podemos simplemente enrollar la matriz nuevamente. Si\(n = 2\), una moneda podría ser utilizada para realizar el experimento.

Estaremos particularmente interesados en repetir un experimento casual una gran cantidad de veces. Si bien el dado cilíndrico sería una forma conveniente de llevar a cabo algunas repeticiones, sería difícil llevar a cabo una gran cantidad de experimentos. Dado que la computadora moderna puede hacer una gran cantidad de operaciones en muy poco tiempo, es natural recurrir a la computadora para esta tarea.

Números Aleatorios

Primero debemos encontrar un análogo de computadora de enrollar un dado. Esto se hace en la computadora por medio de un Dependiendo del paquete de software particular, se le puede pedir a la computadora un número real entre 0 y 1, o un número entero en un conjunto dado de enteros consecutivos. En el primer caso, los números reales se eligen de tal manera que la probabilidad de que el número se encuentre en cualquier subintervalo particular de este intervalo unitario es igual a la longitud del subintervalo. En el segundo caso, cada entero tiene la misma probabilidad de ser elegido.

Dejar\(X\) ser una variable aleatoria con función de distribución\(m(\omega)\), donde\(\omega\) está en el conjunto\(\{\omega_1, \omega_2, \omega_3\}\), y\(m(\omega_1) = 1/2\),\(m(\omega_2) = 1/3\), y\(m(\omega_3) = 1/6\). Si nuestro paquete de computadora puede devolver un entero aleatorio en el conjunto\(\{1, 2, ..., 6\}\), entonces simplemente le pedimos que lo haga, y hacemos que 1, 2 y 3 correspondan a\(\omega_1\), 4 y 5 corresponden a\(\omega_2\), y 6 corresponden a\(\omega_3\). Si nuestro paquete de computadora devuelve un número real aleatorio\(r\) en el intervalo\((0,~1)\), entonces la expresión\[\lfloor {6r}\rfloor + 1\] será un entero aleatorio entre 1 y 6. (La notación\(\lfloor x \rfloor\) significa que el entero más grande no excede\(x\), y se lee “piso de\(x\).”)

El método mediante el cual se generan números reales aleatorios en una computadora se describe en la discusión histórica al final de esta sección. El siguiente ejemplo da la salida de muestra del programa RandomNumbers.

Ejemplo\(\PageIndex{1}\): Random Number Generation

El programa RandomNumbers genera números reales\(n\) aleatorios en el intervalo\([0, 1]\), donde\(n\) es elegido por el usuario. Cuando ejecutamos el programa con\(n = 20\), obtuvimos los datos que se muestran en la Tabla\(\PageIndex{1}\)

Salida de muestra del programa RandomNumbers.

.203309	.762057	.151121	.623868
.932052	.415178	.716719	.967412
.069664	.670982	.352320	.049723
.750216	.784810	.089734	.966730
.946708	.380365	.027381	.900794

Ejemplo\(\PageIndex{2}\): Coin Tossing

Como hemos señalado, nuestra intuición sugiere que la probabilidad de obtener una cabeza en un solo lanzamiento de una moneda es de 1/2. Para que la computadora lance una moneda, podemos pedirle que elija un número real aleatorio en el intervalo\([0, 1]\) y pruebe para ver si este número es menor a 1/2. Si es así, llamaremos al resultado; si no lo llamamos Otra forma de proceder sería pedirle a la computadora que escoja un entero aleatorio del conjunto\(\{0, 1\}\). El programa CoinTosses lleva a cabo el experimento de lanzar una moneda\(n\) veces. Ejecutar este programa, con\(n = 20\), resultó en:

\[THTTTHTTTTHTTTTTHHTT\]

Tenga en cuenta que en 20 lanzamientos, obtuvimos 5 cabezas y 15 colas. Echemos una moneda\(n\) veces, donde\(n\) es mucho mayor que 20, y veamos si obtenemos una proporción de cabezas más cercana a nuestra conjetura intuitiva de 1/2. El programa CoinTosses realiza un seguimiento del número de cabezas. Cuando ejecutamos este programa con\(n = 1000\), obtuvimos 494 cabezas. Cuando lo corrimos con\(n = 10000\), obtuvimos 5039 cabezas.

Notamos que cuando lanzamos la moneda 10,000 veces, la proporción de cabezas estaba cerca del “valor verdadero” .5 para obtener una cabeza cuando se lanza una moneda. Un modelo matemático para este experimento se llama Bernoulli Trials (ver Capítulo 3). El que estudiaremos más adelante (ver Capítulo 8), demostrará que en el modelo de Bernoulli Trials, la proporción de cabezas debe ser cercana a .5, consistente con nuestra idea intuitiva de la interpretación de frecuencia de la probabilidad.

Por supuesto, nuestro programa podría modificarse fácilmente para simular monedas para las que está la probabilidad de una cabeza\(p\), donde\(p\) hay un número real entre 0 y 1.

En el caso del lanzamiento de monedas, ya sabíamos la probabilidad de que el evento ocurriera en cada experimento. El verdadero poder de la simulación proviene de la capacidad de estimar probabilidades cuando no se conocen con anticipación. Este método ha sido utilizado en los recientes descubrimientos de estrategias que hacen que el juego de casino de blackjack sea favorable para el jugador. Ilustramos esta idea en una situación sencilla en la que podemos calcular la verdadera probabilidad y ver qué tan efectiva es la simulación.

Ejemplo\(\PageIndex{3}\): Dice Rolling

Consideramos un juego de dados que jugó un papel importante en el desarrollo histórico de la probabilidad. Las famosas cartas entre Pascal y Fermat, que muchos creen que iniciaron un serio estudio de la probabilidad, fueron instigadas por una solicitud de ayuda de un noble y jugador francés, Chevalier de Méré. Se dice que de Méré había estado apostando a que, en cuatro rollos de dado, aparecería al menos un seis. Estaba ganando consistentemente y, para conseguir que más gente jugara, cambió el juego para apostar a que, en 24 tiradas de dos dados, aparecerían un par de seises. Se afirma que de Méré perdió con 24 y consideró que se necesitaban 25 rollos para que el juego fuera favorable. Fue que las matemáticas estaban equivocadas.

Intentaremos ver si de Méré está en lo correcto simulando sus diversas apuestas. El programa DeMere1 simula una gran cantidad de experimentos, viendo, en cada uno, si un seis aparece en cuatro rollos de un dado. Cuando ejecutamos este programa por 1000 jugadas, un seis surgió en los primeros cuatro rollos 48.6 por ciento del tiempo. Cuando lo ejecutamos por 10,000 jugadas esto sucedió 51.98 por ciento del tiempo.

Observamos que el resultado de la segunda racha sugiere que de Méré estuvo en lo cierto al creer que su apuesta con un dado era favorable; sin embargo, si hubiéramos basado nuestra conclusión en la primera corrida, habríamos decidido que se equivocaba. Los resultados precisos por simulación requieren una gran cantidad de experimentos.

El programa DeMere2 simula la segunda apuesta de Méré de que un par de seises ocurrirá en\(n\) tiradas de un par de dados. La simulación anterior muestra que es importante saber cuántos ensayos debemos simular para esperar cierto grado de precisión en nuestra aproximación. Veremos más adelante que en este tipo de experimentos, una regla general aproximada es que, al menos el 95% de las veces, el error no excede el recíproco de la raíz cuadrada del número de ensayos. Afortunadamente, para este juego de dados, será fácil calcular las probabilidades exactas. Demostraremos en la siguiente sección que para la primera apuesta la probabilidad de que gane de Méré es\(1 - (5/6)^4 = .518\).

Uno puede entender este cálculo de la siguiente manera: La probabilidad de que no 6 aparezca en el primer lanzamiento es\((5/6)\). La probabilidad de que no aparezca 6 en cualquiera de los dos primeros tiros es\((5/6)^2\). Razonando de la misma manera, la probabilidad de que no 6 aparezca en alguno de los primeros cuatro tiradas es\((5/6)^4\). Así, la probabilidad de al menos un 6 en los primeros cuatro tiradas es\(1 - (5/6)^4\). De igual manera, para la segunda apuesta, con 24 tiradas, la probabilidad de que de Méré gane es\(1 - (35/36)^{24} = .491\), y para 25 rollos lo es\(1 - (35/36)^{25} = .506\).

Usando la regla general mencionada anteriormente, requeriría 27,000 rollos para tener una oportunidad razonable de determinar estas probabilidades con suficiente precisión para afirmar que se encuentran en lados opuestos de .5. Es interesante reflexionar si un jugador puede detectar tales probabilidades con la precisión requerida a partir de la experiencia de juego. Algunos escritores sobre la historia de la probabilidad sugieren que de Méré estaba, de hecho, solo interesado en estos problemas como intrigantes problemas de probabilidad.

Figura\(\PageIndex{1}\)

Ejemplo\(\PageIndex{4}\): Heads or Tails

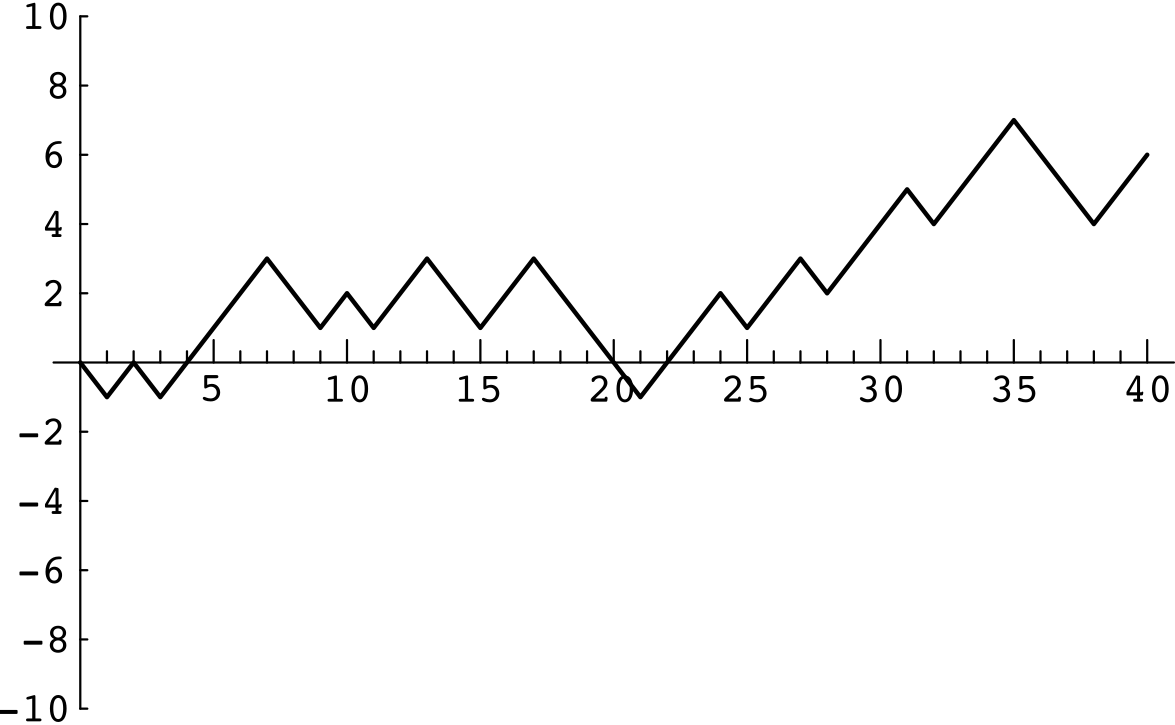
Para nuestro siguiente ejemplo, consideramos un problema donde la respuesta exacta es difícil de obtener pero para el cual la simulación da fácilmente los resultados cualitativos. Peter y Paul juegan un juego llamado En este juego, una moneda justa se arroja una secuencia de veces, elegimos 40. Cada vez que sube una cabeza Peter gana 1 centavo de Pablo, y cada vez que le sube una cola Peter pierde 1 centavo ante Pablo. Por ejemplo, si los resultados de los 40 lanzamientos son

\[\text{THTHHHHTTHTHHTTHHTTTTHHHTHHTHHHTHHHTTTHH}\]

Las ganancias de Peter se pueden graficar como en la Figura\(\PageIndex{1}\)

Peter ha ganado 6 centavos en este juego en particular. Es natural pedir la probabilidad de que gane\(j\) centavos; aquí\(j\) podría haber cualquier número par de\(-40\) a\(40\). Es razonable adivinar que el valor de\(j\) con la probabilidad más alta es\(j = 0\), ya que esto ocurre cuando el número de cabezas es igual al número de colas. De igual manera, adivinaríamos que los valores de\(j\) con las probabilidades más bajas son\(j = \pm 40\).

Una segunda pregunta interesante sobre este juego es la siguiente: ¿Cuántas veces en los 40 tiradas estará Peter a la cabeza? Al mirar la gráfica de sus ganancias (Figura\(\PageIndex{1}\)), vemos que Peter está a la cabeza cuando sus ganancias son positivas, pero tenemos que hacer alguna convención cuando sus ganancias son 0 si queremos que todos los lanzamientos contribuyan al número de veces en la cabeza. Adoptamos la convención de que, cuando las ganancias de Peter son 0, está a la cabeza si estaba por delante en el lanzamiento anterior y no si estaba atrás en el lanzamiento anterior. Con esta convención, Peter está a la cabeza 34 veces en nuestro ejemplo. Nuevamente, nuestra intuición podría sugerir que el número más probable de veces para estar a la cabeza es 1/2 de 40, o 20, y los números menos probables son los casos extremos de 40 o 0.

Es fácil resolver esto simulando el juego una gran cantidad de veces y haciendo un seguimiento de la cantidad de veces que son las ganancias finales de Peter\(j\), y la cantidad de veces que Peter termina liderando\(k\). Las proporciones sobre todos los juegos dan entonces estimaciones para las probabilidades correspondientes. El programa HTSimulation realiza esta simulación. Tenga en cuenta que cuando hay un número par de tiradas en el juego, es posible estar a la cabeza solo un número par de veces. Hemos simulado este juego 10 mil veces. Los resultados se muestran en las Figuras (Figura\(\PageIndex{2}\)) y (Figura\(\PageIndex{3}\)). Estas gráficas, que llamamos gráficas de picos, se generaron utilizando el programa Spikegraph. La línea vertical, o espiga, en posición\(x\) sobre el eje horizontal, tiene una altura igual a la proporción de resultados que es igual\(x\). Nuestra intuición sobre las ganancias finales de Peter era bastante correcta, pero nuestra intuición sobre el número de veces que Peter estuvo a la cabeza estaba completamente equivocada. La simulación sugiere que el número de veces menos probable en el plomo es 20 y el más probable es 0 o 40. Esto es ciertamente correcto, y la explicación para ello se sugiere jugando el juego de cabezas o colas con gran cantidad de lanzamientos y mirando una gráfica de las ganancias de Peter. En la Figura (Figura\(\PageIndex{4}\)) se muestran los resultados de una simulación del juego, para 1000 tiradas y en Figura (Figura\(\PageIndex{5}\)) para 10,000 tiradas.

En el segundo ejemplo Peter se adelantó la mayor parte del tiempo. Es un hecho notable, sin embargo, que, si el juego se continúa el tiempo suficiente, las ganancias de Peter seguirán volviendo a 0, pero habrá tiempos muy largos entre los tiempos que esto suceda. Estos y los resultados relacionados se discutirán en el Capítulo 12.

En todos nuestros ejemplos hasta ahora, hemos simulado resultados equiprobables. Ilustramos a continuación un ejemplo donde los resultados no son equiprobables.

Ejemplo\(\PageIndex{5}\): Horse Races

Cuatro caballos (Acorn, Balky, Chestnut y Dolby) han corrido muchas veces. Se estima que Acorn gana 30 por ciento de las veces, Balky 40 por ciento de las veces, Chestnut 20 por ciento de las veces, y Dolby 10 por ciento de las veces.

Podemos hacer que nuestra computadora realice una carrera de la siguiente manera: Elija un número aleatorio\(x\). Si\(x < .3\) entonces decimos que ganó Acorn. Si\(.3 \le x < .7\) entonces gana Balky. Si\(.7 \le x < .9\) entonces gana Chestnut. Por último, si\(.9 \le x\) entonces gana Dolby.

El programa HorseRace utiliza este método para simular los resultados de\(n\) las carreras. Al ejecutar este programa para\(n = 10\) encontramos que Acorn ganó 40 por ciento de las veces, Balky 20 por ciento de las veces, Chestnut 10 por ciento de las veces, y Dolby 30 por ciento de las veces.

Sería necesario un mayor número de carreras para tener mejor acuerdo con la experiencia pasada. Por lo tanto ejecutamos el programa para simular 1000 carreras con nuestros cuatro caballos. Aunque muy cansados después de todas estas carreras, se desempeñaron de una manera bastante consistente con nuestras estimaciones de sus habilidades. Acorn ganó 29.8 por ciento de las veces, Balky 39.4 por ciento, Chestnut 19.5 por ciento y Dolby 11.3 por ciento de las veces.

El programa GeneralSimulation utiliza este método para simular repeticiones de un experimento arbitrario con un número finito de resultados que ocurren con probabilidades conocidas.

Figura\(\PageIndex{2}\)

Figura\(\PageIndex{3}\)

Figura\(\PageIndex{4}\)

Figura\(\PageIndex{5}\)

Observaciones Históricas

Cualquiera que juegue el mismo juego de azar una y otra vez realmente está realizando una simulación, y en este sentido el proceso de simulación ha estado sucediendo durante siglos. Como hemos comentado, muchos de los primeros problemas de probabilidad bien podrían haber sido sugeridos por las experiencias de los jugadores.

Es natural que cualquiera que intente entender la teoría de la probabilidad intente experimentos simples lanzando monedas, lanzando dados, etc. El naturalista Buffon arrojó una moneda 4040 veces, resultando en 2048 cabezas y 1992 colas. También estimó el número\(\pi\) lanzando agujas sobre una superficie reglada y registrando cuántas veces las agujas cruzaron una línea El biólogo inglés W. F. R. Weldon ¹ registró 26,306 lanzamientos de 12 dados, y el científico suizo Rudolf Wolf ² registró 100,000 lanzamientos de un solo dado sin computadora. Tales experimentos consumen mucho tiempo y pueden no representar con precisión los fenómenos de azar que se están estudiando. Por ejemplo, para los experimentos de dados de Weldon y Wolf, un análisis posterior de los datos registrados mostró un sesgo sospechoso en los dados. El estadístico Karl Pearson analizó una gran cantidad de resultados en ciertas mesas de ruleta y sugirió que las ruedas estaban sesgadas. Escribió en 1894:

Claramente, dado que el Casino no sirve al valioso final de enorme laboratorio para la elaboración de estadísticas de probabilidad, no tiene científicos ¡Los hombres de ciencia no pueden hacer pasar por alto sus teorías más refinadas de esta manera desvergonzada! El Gobierno francés debe ser exhortado por la jerarquía de la ciencia a cerrar los juegos-salones; sería, por supuesto, un acto grácil entregar los recursos restantes del Casino a la Académie des Sciences para la dotación de un laboratorio de probabilidad ortodoxa; en particular, de la nueva rama de esa estudio, la aplicación de la teoría del azar a los problemas biológicos de la evolución, que es probable que ocupe gran parte de los pensamientos de los hombres en un futuro próximo. ³

Sin embargo, estos primeros experimentos fueron sugerentes y condujeron a importantes descubrimientos en probabilidad y estadística. Condujeron a Pearson a lo que es de gran importancia para probar si los datos observados se ajustan a una distribución de probabilidad dada.

A principios de 1900 estaba claro que se necesitaba una mejor manera de generar números aleatorios. En 1927, L. H. C. Tippett publicó una lista de 41.600 dígitos obtenidos al seleccionar números al azar de los reportes censales. En 1955, RAND Corporation imprimió una tabla de 1,000,000 de números aleatorios generados a partir del ruido electrónico. El advenimiento de la computadora de alta velocidad planteó la posibilidad de generar números aleatorios directamente en la computadora, y a fines de la década de 1940 John von Neumann sugirió que esto se hiciera de la siguiente manera: Supongamos que desea una secuencia aleatoria de números de cuatro dígitos. Elija cualquier número de cuatro dígitos, digamos 6235, para comenzar. Cuadrar este número para obtener 38,875,225. Para el segundo número elige los cuatro dígitos del medio de este cuadrado (es decir, 8752). Haz el mismo proceso comenzando con 8752 para obtener el tercer número, y así sucesivamente.

Los métodos más modernos implican el concepto de aritmética modular. Si\(a\) es un entero y\(m\) es un entero positivo, entonces por\(a\ (\mbox{mod}\ m)\) nos referimos al resto cuando\(a\) se divide por\(m\). Por ejemplo,\(10\ ( \mbox{mod}\ 4) = 2\),\(8\ (\mbox{mod}\ 2) = 0\), y así sucesivamente. Para generar una secuencia aleatoria\(X_0, X_1, X_2, \dots\) de números, elija un número inicial\(X_0\) y luego obtenga\(X_{n+1}\) los números\(X_n\) por la fórmula

\[X_{n+1} = (aX_n + c)) (\text{ mod m}),\]

donde\(a\),\(c\), y\(m\) son constantes cuidadosamente escogidas. La secuencia\(X_0, X_1,\)\(X_2, \dots\) es entonces una secuencia de números enteros entre 0 y\(m-1\). Para obtener una secuencia de números reales en\([0,1)\), dividimos cada uno\(X_j\) por\(m\). La secuencia resultante consiste en números racionales de la forma\(j/m\), donde\(0 \leq j \leq m-1\). Dado que\(m\) suele ser un entero muy grande, pensamos en los números en la secuencia como números reales aleatorios en\([0, 1)\).

Tanto para el método de cuadratura de von Neumann como para la técnica aritmética modular, la secuencia de números está realmente completamente determinada por el primer número. Así, no hay nada realmente aleatorio en estas secuencias. Sin embargo, producen números que se comportan mucho como la teoría predeciría para experimentos aleatorios. Para obtener diferentes secuencias para diferentes experimentos\(X_0\) se elige el número inicial mediante algún otro procedimiento que podría implicar, por ejemplo, la hora del día. ⁴

Durante la Segunda Guerra Mundial, los físicos del Laboratorio Científico Los Álamos necesitaron conocer, para fines de blindaje, hasta qué punto viajan los neutrones a través de diversos materiales. Esta pregunta estaba fuera del alcance de los cálculos teóricos. Daniel McCracken, escribiendo en el, afirma:

Los físicos tenían la mayor parte de los datos necesarios: sabían la distancia promedio que viajaría un neutrón de una velocidad dada en una sustancia dada antes de que chocara con un núcleo atómico, cuáles eran las probabilidades de que el neutrón rebotara en lugar de ser absorbido por el núcleo, cuánta energía el neutrón era probable que perdiera después de una colisión dada y así sucesivamente. ⁵

John von Neumann y Stanislas Ulam sugirieron que el problema se resolviera modelando el experimento por dispositivos fortuitos en una computadora. Siendo su trabajo secreto, era necesario darle un nombre en clave. Von Neumann eligió el nombre de “Montecarlo”. Desde entonces, este método de simulación se ha denominado el

William Feller indicó las posibilidades de utilizar simulaciones por computadora para ilustrar conceptos básicos en probabilidad en su libro Al discutir el problema sobre el número de veces en cabeza en el juego de “cabezas o colas” Feller escribe:

Los resultados relativos a las fluctuaciones en el lanzamiento de monedas muestran que las creencias ampliamente difundidas sobre la ley de los grandes números son falaces. Estos resultados son tan sorprendentes y tan divergentes con la intuición común que incluso colegas sofisticados dudaron de que las monedas realmente se portan mal como predice la teoría. Por lo tanto, se incluye el registro de un experimento simulado. ⁶

Feller proporciona una gráfica que muestra el resultado de 10,000 jugadas de similar a la de la Figura\(\PageIndex{5}\)

El sistema de apuestas martingala descrito en Ejercicio\(\PageIndex{10}\) tiene una larga e interesante historia. Russell Barnhart señaló a los autores que su uso se remonta al menos a 1754, cuando Casanova, escribiendo en sus memorias, Historia de mi vida, escribe

Ella [la amante de Casanova] me hizo prometer ir al casino [el Ridotto en Venecia] por dinero para jugar en asociación con ella. Fui allí y me llevé todo el oro que encontré, y, doblando decididamente mis apuestas según el sistema conocido como la martingala, gané tres o cuatro veces al día durante el resto del Carnaval. Nunca perdí la sexta carta. Si lo hubiera perdido, debería haberme quedado sin fondos, lo que ascendió a dos mil zecchini. ⁷

Aunque no hubiera ceros en la rueda de la ruleta así que el juego era perfectamente justo, el sistema martingala, o cualquier otro sistema para el caso, no puede convertir el juego en un juego favorable. La idea de que un juego limpio sigue siendo justo y los juegos injustos siguen siendo injustos bajo los sistemas de juego ha sido explotada por matemáticos para obtener resultados importantes en el estudio de la probabilidad. Introduciremos el concepto general de una martingala en el Capítulo 6.

La palabra en sí también tiene una historia interesante. El origen de la palabra es oscuro. Una versión reciente del da ejemplos de su uso a principios del siglo XVI y dice que su probable origen es la referencia en el Libro Uno de Rabelais, Capítulo 20:

Todo se hizo según lo planeado, siendo lo único que Gargantua dudaba de que pudieran encontrar, enseguida, calzones adecuados a las piernas del viejo compañero; estaba dudoso, también, en cuanto a qué corte estaría más llegando al orador—la martingala, que tiene efecto puente levadizo en el asiento, para permitir hacer el negocio de uno más fácilmente; el estilo marinero, que brinda más comodidad para los riñones; el suizo, que es más cálido en el vientre; o la cola de bacalao, que es más fresca en los lomos. ⁸

Dominic Lusinchi señaló una ocurrencia anterior de la palabra martingala. Según el diccionario francés Le Petit Robert, la palabra proviene de la palabra provenzal “martegalo”, que significa “de Martigues”. Martigues es un pueblo al oeste de Mersela. El diccionario da el ejemplo de “chausses à la martinguale” (que significa calzones estilo Martigues) y la fecha 1491.

En usos modernos la martingala tiene varios significados diferentes, todos relacionados además con el uso del juego de azar. Por ejemplo, es una correa en el arnés de un caballo que se usa para sujetar la cabeza del caballo, y también parte de una plataforma de vela utilizada para sujetar al bauprit.

El sistema Labouchere descrito en Ejercicio\(\PageIndex{9}\) lleva el nombre de Henry du Pre Labouchere (1831—1912), periodista inglés y miembro del Parlamento. Labouchere atribuyó el sistema a Condorcet. Condorcet (1743—1794) fue un líder político durante la época de la revolución francesa que estaba interesado en aplicar la teoría de la probabilidad a la economía y la política. Por ejemplo, calculó la probabilidad de que un jurado que utilice el voto mayoritario dé una decisión correcta si cada jurado tiene la misma probabilidad de decidir correctamente. Sus escritos aportaron una gran cantidad de ideas sobre cómo la probabilidad podría aplicarse a los asuntos humanos. ⁹

Ejercicio\(\PageIndex{1}\)

Modificar el programa CoinTosses para lanzar una moneda\(n\) veces e imprimir después de cada 100 lanzas la proporción de cabezas menos 1/2. ¿Estos números parecen acercarse a 0 a medida que\(n\) aumenta? Modifique nuevamente el programa para imprimir, cada 100 veces, ambas de las siguientes cantidades: la proporción de cabezas menos 1/2, y el número de cabezas menos la mitad del número de lanzamientos. ¿Estos números parecen acercarse a 0 a medida que\(n\) aumenta?

Ejercicio\(\PageIndex{2}\)

Modificar el programa CoinTosses para que arroje una moneda\(n\) veces y registre si la proporción de cabezas está o no dentro de .1 de .5 (es decir, entre .4 y .6). Haga que su programa repita este experimento 100 veces. Acerca de qué tan grande debe\(n\) ser para que aproximadamente 95 de cada 100 veces la proporción de cabezas esté entre .4 y .6?

Ejercicio\(\PageIndex{3}\)

A principios del 1600, se le pidió a Galileo que explicara el hecho de que, aunque el número de triples de enteros de 1 a 6 con suma 9 es el mismo que el número de tales triples con suma 10, cuando se tiran tres dados, un 9 parecía aparecer con menos frecuencia que un 10 —supuestamente en la experiencia de los apostadores.

1. Escribe un programa para simular el tirado de tres dados una gran cantidad de veces y realizar un seguimiento de la proporción de veces que la suma es 9 y la proporción de veces que es 10.

2. ¿Se puede concluir a partir de sus simulaciones que los jugadores tenían razón?

Ejercicio\(\PageIndex{4}\)

En raquetball, una jugadora sigue sirviendo mientras esté ganando; un punto se anota sólo cuando un jugador está sirviendo y gana la volea. El primer jugador en ganar 21 puntos gana el juego. Asume que sirves primero y tienes una probabilidad .6 de ganar una volea cuando sirves y probabilidad .5 cuando tu oponente sirve. Estima, por simulación, la probabilidad de que ganes un juego.

Ejercicio\(\PageIndex{5}\)

Considera la apuesta de que los tres dados subirán seises al menos una vez en\(n\) tiradas de tres dados. Calcular\(f(n)\), la probabilidad de al menos un triple-seis cuando se lanzan tres dados\(n\) veces. Determinar el valor más pequeño de\(n\) necesario para una apuesta favorable de que se producirá un triple-seis cuando se tiran tres dados\(n\) veces. (Demoivre diría que debería ser sobre\(216\log 2 = 149.7\) y así respondería 150—ver Ejercicio\(\PageIndex{16}\) ¿Estás de acuerdo con él?)

Ejercicio\(\PageIndex{6}\)

En Las Vegas, una rueda de ruleta tiene 38 ranuras numeradas 0, 00, 1, 2,..., 36. Las ranuras 0 y 00 son verdes y la mitad de las 36 ranuras restantes son rojas y la mitad son negras. Un crupier hace girar la rueda y lanza una bola de marfil. Si apuestas 1 dólar en rojo, ganas 1 dólar si la pelota se detiene en una ranura roja y de lo contrario pierdes 1 dólar. Escribe un programa para encontrar las ganancias totales para un jugador que haga 1000 apuestas en rojo.

Ejercicio\(\PageIndex{7}\)

Otra forma de apuesta para la ruleta es apostar a que aparecerá un número específico (digamos 17). Si la pelota se detiene en tu número, recuperas tu dólar más 35 dólares. Si no, pierdes tu dólar. Escribe un programa que trazará tus ganancias cuando hagas 500 jugadas de ruleta en Las Vegas, primero cuando apuestes cada vez en rojo (ver Ejercicio\(\PageIndex{6}\)), y luego para una segunda visita a

Ejercicio\(\PageIndex{8}\)

Un estudiante astuto notó que, en nuestra simulación del juego de cabezas o colas (ver Ejemplo\(\PageIndex{3}\)), la proporción de veces que el jugador siempre está a la cabeza es muy cercana a la proporción de veces que las ganancias totales del jugador terminan siendo 0. Calcula estas probabilidades mediante la enumeración de todos los casos para dos tiradas y para cuatro tiradas, y mira si piensas que estas probabilidades son, de hecho, las mismas.

Ejercicio\(\PageIndex{9}\)

El para la ruleta se juega de la siguiente manera. Anote una lista de números, generalmente 1, 2, 3, 4. Apuesta la suma del primero y último,\(1 + 4 = 5\), en rojo. Si ganas, elimina el primer y último número de tu lista. Si pierdes, agrega la cantidad que apostaste por última vez al final de tu lista. Después usa la nueva lista y apuesta la suma del primer y último número (si solo hay un número, apuesta esa cantidad). Continúa hasta que tu lista quede vacía. Demuestre que, si esto sucede, gana la suma,\(1 + 2 + 3 + 4 = 10\), de su lista original. Simula este sistema y mira si siempre te detienes y, de ahí, siempre ganas. Si es así, ¿por qué no es este un sistema de juego infalible?

Ejercicio\(\PageIndex{10}\)

Otro sistema de juego bien conocido es el. Supongamos que estás apostando al rojo para que aparezca en la ruleta. Cada vez que ganes, apuesta 1 dólar la próxima vez. Cada vez que pierdes, duplica tu apuesta anterior. Supongamos que usa este sistema hasta que haya ganado al menos 5 dólares o haya perdido más de 100 dólares. Escribe un programa para simular esto y jugarlo varias veces y ver cómo te va. En su libro W. M. Thackeray comenta “¿Aún no has jugado? No lo hagas; sobre todo evita una martingala si lo haces”. ¹⁰ ¿Fue este un buen consejo?

Ejercicio\(\PageIndex{11}\)

Modificar el programa HTSimulation para que haga un seguimiento del máximo de las ganancias de Peter en cada juego de 40 tiradas. Haga que su programa imprima la proporción de veces que sus ganancias totales toman en valores\(0,\ 2,\ 4,\ \dots,\ 40\). Calcula las probabilidades exactas correspondientes para juegos de dos tiradas y cuatro tiradas.

Ejercicio\(\PageIndex{12}\)

En una próxima elección nacional para el Presidente de Estados Unidos, un encuestador planea predecir al ganador del voto popular tomando una muestra aleatoria de 1000 votantes y declarando que el ganador será el que obtenga más votos en su muestra. Supongamos que 48 por ciento de los votantes planean votar por el candidato republicano y 52 por ciento planean votar por el candidato demócrata. Para tener una idea de lo razonable que es el plan del encuestador, escribe un programa para hacer esta predicción por simulación. Repita la simulación 100 veces y vea cuántas veces se haría realidad la predicción del encuestador. Repita su experimento, asumiendo ahora que el 49 por ciento de la población planea votar por el candidato republicano; primero con una muestra de 1000 y después con una muestra de 3000. (La Encuesta Gallup utiliza alrededor de 3000.) (Esta idea se discute más a fondo en el Capítulo 9, Sección 9.1.)

Ejercicio\(\PageIndex{13}\)

El psicólogo Tversky y sus compañeros ¹¹ dicen que alrededor de cuatro de cada cinco personas responderán (a) a la siguiente pregunta:

Cierto pueblo es atendido por dos hospitales. En el hospital más grande nacen unos 45 bebés cada día, y en el hospital más pequeño nacen 15 bebés cada día. Si bien la proporción general de niños es de alrededor del 50 por ciento, la proporción real en cualquiera de los hospitales puede ser mayor o menor del 50 por ciento en cualquier día. Al cierre de un año, ¿qué hospital tendrá el mayor número de días en los que más del 60 por ciento de los bebés nacidos fueron niños?

1. el hospital grande

2. el pequeño hospital

3. ni siquiera, el número de días será aproximadamente el mismo.

Supongamos que la probabilidad de que un bebé sea un niño es .5 (las estimaciones reales hacen que esto sea más como .513). Decidir, por simulación, cuál es la respuesta correcta a la pregunta. ¿Puedes sugerir por qué tanta gente se equivoca?

Ejercicio\(\PageIndex{14}\)

Se te ofrece el siguiente juego. Una moneda justa será arrojada hasta la primera vez que salga de cabeza. Si esto ocurre en el\(j\) th lanzamiento se le pagan\(2^j\) dólares. Seguro que ganarás al menos 2 dólares así que deberías estar dispuesto a pagar para jugar a este juego, pero ¿cuánto? Pocas personas pagarían hasta 10 dólares por jugar a este juego. A ver si puedes decidir, por simulación, una cantidad razonable que estarías dispuesto a pagar, por juego, si se te permitirá hacer una gran cantidad de jugadas del juego. ¿La cantidad que estarías dispuesto a pagar por juego depende del número de jugadas que se te permitirán?

Ejercicio\(\PageIndex{15}\)

Tversky y sus colegas ¹² estudiaron los récords de 48 de los partidos de basquetbol de los Philadelphia 76ers en la temporada 1980-81 para ver si un jugador tenía momentos en los que estaba caliente y cada disparo entraba, y otras ocasiones en las que tenía frío y apenas podía golpear el tablero. Los jugadores estimaron que tenían alrededor de 25 por ciento más probabilidades de hacer un tiro tras un golpe que después de una falla. De hecho, lo contrario era cierto: los 76ers tenían 6 por ciento más probabilidades de anotar después de un fallo que después de un hit. Tversky reporta que el número de rayas calientes y frías era sobre lo que uno esperaría por efectos puramente aleatorios. Suponiendo que un jugador tiene cincuenta y cincuenta posibilidades de hacer un tiro y hace 20 tiros por juego, estime por simulación la proporción de los juegos en los que el jugador tendrá una racha de 5 o más hits.

Ejercicio\(\PageIndex{16}\)

Estimar, por simulación, el promedio de niños que habría en una familia si todas las personas tuvieran hijos hasta que tuvieran un niño. Haga lo mismo si todas las personas tuvieron hijos hasta que tuvieron al menos un niño y al menos una niña. ¿Cuántos niños más esperarías encontrar bajo el segundo esquema que bajo el primero de 100 mil familias? (Supongamos que los niños y las niñas son igualmente probables.)

Ejercicio\(\PageIndex{17}\)

Se sabe que los matemáticos obtienen algunas de las mejores ideas mientras están sentados en un café, viajan en autobús o pasean por el parque. A principios de la década de 1900 el famoso matemático George Pólya vivía en un hotel cerca del bosque en Zúrich. Le gustaba caminar por el bosque y pensar en matemáticas. Pólya describe el siguiente incidente:

En el hotel vivían también algunos estudiantes con los que solía tomar mis comidas y tenía relaciones amistosas. En cierto día uno de ellos esperaba la visita de su prometida, lo que (sic) yo sabía, pero no preveía que él y su prometida también saldrían a dar un paseo por el bosque, y luego de pronto los encontré allí. Y luego los conocí la misma mañana repetidamente, no recuerdo cuántas veces, pero ciertamente con demasiada frecuencia y me sentí avergonzado: Parecía como si estuviera husmeando alrededor lo cual era, te lo aseguro, no es el caso. ¹³

Esto lo puso a pensar en si caminantes aleatorios estaban destinados a encontrarse.

Pólya consideró caminantes aleatorios en una, dos y tres dimensiones. En una dimensión, imaginó al andador en una calle muy larga. En cada intersección el caminante arroja una moneda justa para decidir en qué dirección caminar a continuación (ver Figura\(\PageIndex{6}a\)). En dos dimensiones, el andador camina sobre una cuadrícula de calles, y en cada intersección elige una de las cuatro direcciones posibles con igual probabilidad (ver Figura\(\PageIndex{6}b\)). En tres dimensiones (mejor podríamos hablar de un escalador aleatorio), el andador se mueve en una cuadrícula tridimensional, y en cada intersección hay ahora seis direcciones diferentes que el caminante puede elegir, cada una con igual probabilidad (ver Figura\(\PageIndex{6}c\)).

Se remite al lector a la Sección 12.1 donde se discuten éste y problemas relacionados.

1. Escribe un programa para simular una caminata aleatoria en una dimensión comenzando en 0. Haga que su programa imprima las longitudes de los tiempos entre las devoluciones al punto de partida (vuelve a 0). A ver si puedes adivinar a partir de esta simulación la respuesta a la siguiente pregunta: ¿El caminante siempre volverá a su punto de partida eventualmente o podría alejarse para siempre?

2. Los caminos de dos caminantes en dos dimensiones que se encuentran después de\(n\) escalones pueden considerarse como un solo camino que comienza en\((0,0)\) y vuelve a\(2n\) los pasos\((0,0)\) posteriores. Esto significa que la probabilidad de que dos caminantes aleatorios en dos dimensiones se encuentren es la misma que la probabilidad de que un solo andador en dos dimensiones alguna vez regrese al punto de partida. Por lo tanto, la cuestión de si dos caminantes seguramente se reunirán es la misma que la cuestión de si un solo andador seguramente regresará al punto de partida.

   Escribe un programa para simular una caminata aleatoria en dos dimensiones y ver si piensas que el andador seguramente volverá a\((0,0)\). Si es así, Pólya estaría seguro de seguir reuniéndose con sus amigos en el parque. Quizás a estas alturas ya has conjeturado la respuesta a la pregunta: ¿Es seguro que un andador aleatorio en una o dos dimensiones volverá al punto de partida? Pólya respondió a esta pregunta para las dimensiones uno, dos y tres. Estableció el notable resultado de que la respuesta está en una y dos dimensiones y en tres dimensiones.

3. Escribe un programa para simular una caminata aleatoria en tres dimensiones y ver si, a partir de esta simulación y los resultados de (a) y (b), podrías haber adivinado el resultado de Pólya.