2.2: Eventos y Variables Aleatorias
- Page ID
- 152179
El propósito de esta sección es estudiar dos tipos básicos de objetos que forman parte del modelo de un experimento aleatorio. Si eres un nuevo estudiante de probabilidad, simplemente ignora la terminología teórica de medidas y omita los detalles técnicos.
Espacios de muestra
El conjunto de resultados
Recordemos que en un experimento aleatorio, el resultado no se puede predecir con certeza, antes de que se ejecute el experimento. Por otro lado:
Suponemos que podemos identificar un conjunto fijo\( S \) que incluya todos los resultados posibles de un experimento aleatorio. Este conjunto juega el papel del conjunto universal a la hora de modelar el experimento.
Para experimentos simples,\( S \) puede ser precisamente el conjunto de posibles resultados. Más a menudo, para experimentos complejos,\( S \) es un conjunto matemáticamente conveniente que incluye los posibles resultados y quizás otros elementos también. Por ejemplo, si el experimento es lanzar un dado estándar y registrar la partitura que se produce, dejaríamos\(S = \{1, 2, 3, 4, 5, 6\}\), el conjunto de posibles resultados. Por otro lado, si el experimento es capturar una cigarra y medir su peso corporal (en miligramos), podríamos tomar convenientemente\(S = [0, \infty)\), aunque la mayoría de los elementos de este conjunto son imposibles (¡esperamos!). El problema es que quizás no sepamos exactamente los resultados que son posibles. ¿Se puede quemar una bombilla sin falla durante mil horas? ¿Por mil días? por mil años?
A menudo el resultado de un experimento aleatorio consiste en una o más mediciones reales, y así, el\( S \) consiste en todas las secuencias de medición posibles, un subconjunto de\(\R^n\) para algunas\(n \in \N_+\). De manera más general, supongamos que tenemos\(n\) experimentos y ese\( S_i \) es el conjunto de resultados para el experimento\( i \in \{1, 2, \ldots, n\} \). Entonces el producto cartesiano\(S_1 \times S_2 \times \cdots \times S_n\) es el conjunto natural de resultados para el experimento compuesto que consiste en realizar los\(n\) experimentos en secuencia. En particular, si tenemos un experimento básico con\(S\) como conjunto de resultados, entonces\(S^n\) es el conjunto natural de resultados para el experimento compuesto que consiste en\(n\) replicaciones del experimento básico. Del mismo modo, si tenemos una secuencia infinita de experimentos y\( S_i \) es el conjunto de resultados para el experimento\( i \in \N_+ \), entonces\(S_1 \times S_2 \times \cdots\) es el conjunto natural de resultados para el experimento compuesto que consiste en realizar los experimentos dados en secuencia. En particular, el conjunto de resultados para el experimento compuesto que consiste en repeticiones indefinidas de un experimento básico es\(S^\infty = S \times S \times \cdots \). Este es un caso especial esencial, porque la teoría de probabilidad (clásica) se basa en la idea de replicar un experimento dado.
Eventos
Consideremos de nuevo un experimento aleatorio con\( S \) como conjunto de resultados. Ciertos subconjuntos de\( S \) se conocen como eventos. Supongamos que\( A \subseteq S \) es un evento dado, y que el experimento se ejecuta, dando como resultado resultado\( s \in S \).
- Si\( s \in A \) entonces decimos que\( A \) ocurre.
- Si\( s \notin A \) entonces decimos que eso\( A \) no ocurre.
Intuitivamente, debe pensar en un evento como una declaración significativa sobre el experimento: cada declaración de este tipo se traduce en un evento, es decir, el conjunto de resultados para los que la afirmación es verdadera. En particular, en\(S\) sí mismo es un evento; por definición siempre ocurre. En el otro extremo, el conjunto vacío\(\emptyset\) es también un evento; por definición nunca ocurre.
Para una nota sobre terminología, recordemos que un espacio matemático consiste en un conjunto junto con otras estructuras matemáticas definidas en el conjunto. Un ejemplo con el que puede estar familiarizado es un espacio vectorial, que consiste en un conjunto (los vectores) junto con las operaciones de suma y multiplicación escalar. En la teoría de la probabilidad, muchos autores utilizan el término espacio muestral para el conjunto de resultados de un experimento aleatorio, pero aquí está la definición más cuidadosa:
El espacio muestral de un experimento es\( (S, \mathscr S) \) donde\( S \) está el conjunto de resultados y\( \mathscr S \) es la colección de eventos.
Detalles
A veces no todos los subconjuntos de\(S\) pueden ser permitidos como un evento, pero\( \mathscr S \) se requiere que la colección de eventos sea un \( \sigma \)álgebra, de modo que el espacio muestral\( (S, \mathscr S) \) sea un espacio medible. Los axiomas de un\(\sigma\) álgebra aseguran que los nuevos conjuntos que se construyen de manera razonable a partir de eventos dados, utilizando las operaciones de conjunto, sean ellos mismos eventos válidos. La mayoría de los espacios muestrales que ocurren en probabilidad elemental se encuentran en dos categorías generales.
- Discreto:\( S \) es contable y\( \mathscr S = \mathscr P(S) \) es la colección de todos los subconjuntos de\( S \). En este caso, el espacio muestral\((S, \mathscr S)\) es discreto.
- Euclides:\(S\) es un subconjunto medible de\(\R^n\) para algunos\(n \in \N_+\) y\(\mathscr S\) es la colección de subconjuntos medibles de\(S\).
En (b), los subconjuntos mearuables de\(\R^n\) incluyen todos los conjuntos encontrados en el cálculo y en las aplicaciones estándar de la teoría de probabilidad, y muchos más además. No obstante, por razones técnicas, deben excluirse ciertos subconjuntos muy raros. Normalmente\( S \) es un conjunto definido por un número finito de desigualdades que involucran funciones elementales.
El álgebra de los acontecimientos
El álgebra estándar de conjuntos conduce a una gramática para discutir experimentos aleatorios y nos permite construir nuevos eventos a partir de eventos dados. En los siguientes resultados, supongamos que ese\( S \) es el conjunto de resultados de un experimento aleatorio, y que\(A\) y\(B\) son eventos.
\(A \subseteq B\)si y sólo si la ocurrencia de\(A\) implica la ocurrencia de\(B\).
Prueba
Recordemos que\( \subseteq \) es la relación de subconjunto. Entonces por definición,\( A \subseteq B \) significa que eso\( s \in A \) implica\( s \in B \).
\(A \cup B\)es el evento que ocurre si y sólo si\(A\) ocurre u\(B\) ocurre.
Prueba
Recordemos que\( A \cup B \) es la unión de\( A \) y\( B \). Entonces por definición,\( s \in A \cup B \) si y sólo si\( s \in A \) o\( s \in B \).
\(A \cap B\)es el evento que ocurre si y sólo si\(A\) ocurre y\(B\) ocurre.
Prueba
Recordemos que\( A \cap B \) es la intersección de\( A \) y\( B \). Entonces por definiton,\( s \in A \cap B \) si y solo si\( s \in A \) y\( s \in B \).
\(A\)y\(B\) son disjuntos si y sólo si son mutuamente excluyentes; ambos no pueden ocurrir en la misma ejecución del experimento.
Prueba
Por definición,\( A \) y\( B \) disjunta significa eso\( A \cap B = \emptyset \).
\(A^c\)es el evento que ocurre si y sólo si\(A\) no ocurre.
Prueba
Recordemos que\( A^c \) es el complemento de\( A \), así que\( s \in A^c \) si y sólo si\( s \notin A \).
\(A \setminus B\)es el evento que ocurre si y sólo si\(A\) ocurre y\(B\) no ocurre.
Prueba
Recordemos eso\( A \setminus B = A \cap B^c \). De ahí\( s \in A \setminus B \) si y sólo si\( s \in A \) y\( s \notin B \).
\((A \cap B^c) \cup (B \cap A^c)\)es el evento que ocurre si y sólo si ocurre uno pero no ambos eventos dados.
Prueba
Los acontecimientos en el sindicato son disjuntos. Entonces para\( s \) es en el evento dado si y solo si cualquiera\( s \in A \) y\( s \notin B \), o\( s \in B \) y\( s \notin A \).
Recordemos que el evento en (10) es la diferencia simétrica de\(A\) y\(B\), y a veces se denota\(A \Delta B\). Este suceso corresponde a exclusivo o, a diferencia de la unión ordinaria\( A \cup B \) que corresponde a inclusiva o.
\((A \cap B) \cup (A^c \cap B^c)\)es el evento que ocurre si y sólo si se producen ambos o ninguno de los eventos dados.
Prueba
Los acontecimientos en el sindicato son disjuntos. Así\( s \) es en el evento dado si y sólo si cualquiera\( s \in A \) y\( s \in B \), o\( s \notin A \) y\( s \notin B \).
En la aplicación de diagrama Venn, observe el diagrama de cada uno de los 16 eventos que se pueden construir a partir de\(A\) y\(B\).
Supongamos ahora que\(\mathscr{A} = \{A_i: i \in I\}\) es una colección de eventos para el experimento aleatorio, donde\(I\) hay un conjunto de índices contables.
\( \bigcup \mathscr{A} = \bigcup_{i \in I} A_i \)es el evento que ocurre si y sólo si se produce al menos un evento en la colección.
Prueba
Tenga en cuenta que\( s \in \bigcup_{i \in I} A_i \) si y solo si\( s \in A_i \) para algunos\( i \in I \).
\( \bigcap \mathscr{A} = \bigcap_{i \in I} A_i \)es el evento que ocurre si y solo si ocurre cada evento de la colección:
Prueba
Tenga en cuenta que\( s \in \bigcap_{i \in I} A_i \) si y solo si\( s \in A_i \) por cada\( i \in I \).
\(\mathscr{A}\)es una colección disjunta por pares si y solo si los eventos son mutuamente excluyentes; a lo sumo uno de los eventos podría ocurrir en una ejecución determinada del experimento.
Prueba
Por definición,\( A_i \cap A_j = \emptyset \) para distintos\( i, \, j \in I \).
Supongamos ahora que\((A_1, A_2, \ldots\)) es una secuencia infinita de eventos.
\(\bigcap_{n=1}^\infty \bigcup_{i=n}^\infty A_i\)es el evento que ocurre si y sólo si ocurren infinitamente muchos de los eventos dados. A este evento se le llama a veces el límite superior de\((A_1, A_2, \ldots)\).
Prueba
Tenga en cuenta que\( s \) es en el evento dado si y sólo si por cada\( n \in \N_+ \) existe\( i \in \N_+ \) con\( i \ge n \) tal que\( s \in A_i \). A su vez esto significa que\( s \in A_i \) para infinitamente muchos\( i \in I \).
\(\bigcup_{n=1}^\infty \bigcap_{i=n}^\infty A_i\)es el evento que ocurre si y sólo si ocurren todos, pero finitamente muchos de los eventos dados. A este evento se le llama a veces el límite inferior de\((A_1, A_2, \ldots)\).
Prueba
Tenga en cuenta que\( s \) es en el evento dado si y sólo si existe\( n \in \N_+ \) tal que\( s \in A_i \) para cada uno\( i \in \N_+ \) con\( i \ge n \). A su vez, esto significa que\( s \in A_i \) para todos menos finitamente muchos\( i \in I \).
Límite superiores e inferiores se discuten con más detalle en la sección de convergencia.
Variables aleatorias
Intuitivamente, una variable aleatoria es una medida de interés en el contexto del experimento. Ejemplos simples incluyen el número de cabezas cuando una moneda se lanza varias veces, la suma de las puntuaciones cuando se lanza un par de dados, la vida útil de un dispositivo sujeto a estrés aleatorio, el peso de una persona elegida de una población. Muchos más ejemplos se dan a continuación en los ejercicios a continuación. Matemáticamente, una variable aleatoria es una función definida en el conjunto de resultados.
Una función\( X \) de\( S \) dentro de un conjunto\( T \) es una variable aleatoria para el experimento con valores en\( T \).
Detalles
El conjunto también\( T \) vendrá con un\( \sigma \) -álgebra\( \mathscr T \) de subconjuntos admisibles, así que ese\((T, \mathscr T)\) es un espacio medible, al igual que\( (S, \mathscr S) \). Se requiere\( X \) que la función sea medible, una suposición que asegura que las declaraciones significativas que implican\( X \) definir eventos. En la discusión a continuación,\( T \) se supone que todos los subconjuntos de están en\( \mathscr T \).
La probabilidad tiene su propia notación, muy diferente de otras ramas de las matemáticas. Como un caso concreto, las variables aleatorias, aunque sean funciones, generalmente se denotan con letras mayúsculas cerca del final del alfabeto. El uso de una letra cerca del final del alfabeto pretende enfatizar la idea de que el objeto es una variable en el contexto del experimento. El uso de una letra mayúscula pretende enfatizar el hecho de que no se trata de una variable algebraica ordinaria a la que podamos asignar un valor específico, sino más bien una variable aleatoria cuyo valor es indeterminado hasta que ejecutemos el experimento. Específicamente, cuando ejecutamos el experimento\(s \in S\) se produce un resultado, y la variable aleatoria\(X\) toma el valor\(X(s) \in T\).
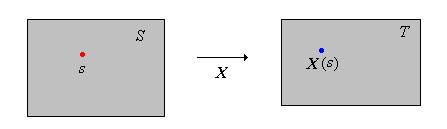
Si\( B \subseteq T \), usamos la notación\( \{X \in B\} \) para la imagen inversa\( \{s \in S: X(s) \in B\} \), en lugar de\( X^{-1}(B) \). Nuevamente, la notación es más natural ya que pensamos en\( X \) ella como una variable en el experimento. Piense en\( \{X \in B\} \) como una declaración sobre\( X \), que luego se traduce en el evento\( \{s \in S: X(s) \in B\} \)
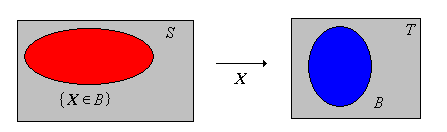
Nuevamente, cada enunciado sobre una variable aleatoria\( X \) con valores en\( T \) se traduce en una imagen inversa de la forma\( \{X \in B\} \) para algunos\( B \in \mathscr T \). Entonces, por ejemplo, si\( x \in T \) entonces\(\{X = x\} = \{X \in \{x\}\} = \left\{s \in S: X(s) = x\right\}\). Si\(X\) es una variable aleatoria de valor real y\( a, \, b \in \R \) con\( a \lt b \) entonces\(\{ a \leq X \leq b\} = \left\{ X \in [a, b]\right\} = \{s \in S: a \leq X(s) \leq b\}\).
Supongamos que\(X\) es una variable aleatoria que toma valores\(T\), y eso\(A, \, B \subseteq T\). Entonces
- \(\{X \in A \cup B\} = \{X \in A\} \cup \{X \in B\}\)
- \(\{X \in A \cap B\} = \{X \in A\} \cap \{X \in B\}\)
- \(\{X \in A \setminus B\} = \{X \in A\} \setminus \{X \in B\}\)
- \(A \subseteq B \implies \{X \in A\} \subseteq \{X \in B\}\)
- Si\(A\) y\(B\) son disjuntos, entonces también lo son\(\{X \in A\}\) y\(\{X \in B\}\).
Prueba
Esto es una reformulación del hecho de que las imágenes inversas de una función preservan las operaciones establecidas; solo cambia la notación (y es más simple).
- \(s \in \{X \in A \cup B\}\)si y sólo si y sólo\(X(s) \in A \cup B\) si\(X(s) \in A\) o si y sólo\(X(s) \in B\) si y sólo si\(s \in \{X \in A\}\) o\(s \in \{X \in B\}\) si y sólo si\(s \in \{X \in A\} \cup \{X \in B\}\).
- La prueba es exactamente la misma que (a), con y sustituyendo o.
- La prueba también es exactamente la misma que (a), con pero no reemplazando o.
- Si\(s \in \{X \in A\}\) entonces es\(X(s) \in A\) así\(X(s) \in B\) y por lo tanto\(s \in \{X \in B\}\).
- Esto se desprende de la parte b).
Al igual que con una función general, el resultado en la parte (a) se mantiene para la unión de una colección contable de subconjuntos, y el resultado en la parte (b) se mantiene para la intersección de una colección contable de subconjuntos. No hay nuevas ideas involucradas; sólo la notación es más complicada.
A menudo, una variable aleatoria toma valores en un subconjunto\(T\) de\(\R^k\) para algunos\(k \in \N_+\). Podríamos expresar una variable aleatoria como\(\bs{X} = (X_1, X_2, \ldots, X_k)\) donde\(X_i\) es una variable aleatoria de valor real para cada una\(i \in \{1, 2, \ldots, k\}\). En este caso, generalmente nos referimos\(\bs{X}\) como un vector aleatorio, para enfatizar su carácter de dimensiones superiores. Una variable aleatoria puede tener una estructura aún más complicada. Por ejemplo, si el experimento consiste en seleccionar\(n\) objetos de una población y registrar diversas mediciones reales para cada objeto, entonces el resultado del experimento es un vector de vectores:\(\bs{X} = (X_1, X_2, \ldots, X_n)\) donde\(X_i\) está el vector de mediciones para el objeto\(i\) th. Hay otras posibilidades; una variable aleatoria podría ser una secuencia infinita, o podría ser valorada por conjuntos. Ejemplos específicos se dan en los ejercicios computacionales a continuación. Sin embargo, el punto importante es simplemente que una variable aleatoria es una función definida en el conjunto de resultados\(S\).
El resultado del experimento en sí puede considerarse como una variable aleatoria. Específicamente, let\(T = S\) y let\(X\) denotan la función identify on\(S\)\(X(s) = s\) para que para\(s \in S\). Entonces trivialmente\(X\) es una variable aleatoria, y los eventos que se pueden definir en términos de\(X\) son simplemente los eventos originales del experimento. Es decir, si\( A \) es un evento entonces\( \{X \in A\} = A \). Por el contrario, cada variable aleatoria define efectivamente un nuevo experimento aleatorio.
En la configuración general anterior, una variable aleatoria\(X\) define un nuevo experimento aleatorio con\( T \) como el nuevo conjunto de resultados y subconjuntos de\( T \) como la nueva colección de eventos.
Detalles
Técnicamente, el\( \sigma \) álgebra\( \mathscr T \) sería la nueva colección de eventos.
De hecho, a menudo un experimento aleatorio se modela especificando las variables aleatorias de interés, en el lenguaje del experimento. Luego, una definición matemática de las variables aleatorias especifica el espacio muestral. Una función (o transformación) de una variable aleatoria define una nueva variable aleatoria.
Supongamos que\( X \) es una variable aleatoria para el experimento con valores en\(T\) y que\( g \) es una función de\( T \) a otro conjunto\( U \). Entonces\( Y = g(X) \) es una variable aleatoria con valores en\( U \).
Detalles
Técnicamente,\( T \) y\( U \) ambos vienen con\(\sigma\) -álgebras de subconjuntos admisibles\( \mathscr T \) y\( \mathscr U \), respectivamente. La función\( g \), al igual que la función\( X \), se requiere que sea medible. Esta suposición asegura que\(Y = g(X)\) es una función medible desde\(S\) dentro\(U\), y por lo tanto es una variable aleatoria válida.
Tenga en cuenta que, como funciones\( g(X) = g \circ X \),, la composición de\( g \) con\( X \). Pero nuevamente, pensando en\( X \) y\( Y \) como variables en el contexto del experimento, la notación\( Y = g(X) \) es mucho más natural.
Variables de indicador
Para un evento\(A\), la función indicadora de\(A\) se llama la variable indicadora de\(A\).
El valor de estas variables aleatorias nos indica si\(A\) ha ocurrido o no: Es\[ \bs{1}_A = \begin{cases} 1, & A \text{ occurs} \\ 0, & A \text{ does not occur} \end{cases} \] decir, en función de\( S \),\[ \bs{1}_A(s) = \begin{cases} 1, & s \in A \\ 0, & s \notin A \end{cases} \]
Si\(X\) es una variable aleatoria que toma los valores 0 y 1, entonces\(X\) es la variable indicadora del evento\(\{X = 1\}\).
Prueba
Tenga en cuenta que para\( s \in S \),\( X(s) = 1\) si\( s \in \{X = 1\} \) y de\( X(s) = 0 \) otra manera.
Recordemos también que el conjunto álgebra de eventos se traduce en el álgebra aritmética de las variables indicadoras.
Supongamos que\(A\) y\(B\) son eventos.
- \(\bs{1}_{A \cap B} = \bs{1}_A \bs{1}_B = \min\left\{\bs{1}_A, \bs{1}_B\right\}\)
- \(\bs{1}_{A \cup B} = 1 - \left(1 - \bs{1}_A\right)\left(1 - \bs{1}_B\right) = \max\left\{\bs{1}_A, \bs{1}_B\right\}\)
- \(\bs{1}_{B \setminus A} = \bs{1}_B \left(1 - \bs{1}_A\right)\)
- \(\bs{1}_{A^c} = 1 - \bs{1}_A\)
- \(A \subseteq B\)si y solo si\(\bs{1}_A \leq \bs{1}_B\)
Los resultados de la parte (a) se extienden a las intersecciones arbitrarias y los resultados en la parte (b) se extienden a las uniones arbitrarias. Si el evento\( A \) tiene una descripción complicada, a veces usamos\( \bs 1 (A) \) para la variable indicadora más bien eso\( \bs 1_A \).
Ejemplos y Aplicaciones
Recordemos que la teoría de la probabilidad a menudo se ilustra usando dispositivos simples de juegos de azar: monedas, dados, cartas, hilanderos, urnas con bolas, etc. Los ejemplos basados en tales dispositivos son pedagógicamente valiosos por su simplicidad y claridad conceptual. Por otro lado, recuerda que la probabilidad no se trata sólo de juegos de azar y juegos de azar. Más bien, tratar de ver los problemas que involucran monedas, dados, etc. como metáforas para problemas más complejos y realistas.
Monedas y dados
El experimento básico de monedas consiste en lanzar una moneda\(n\) veces y registrar la secuencia de partituras\((X_1, X_2, \ldots, X_n)\) (donde 1 denota cabezas y 0 denota colas). Este experimento es un ejemplo genérico de ensayos de\(n\) Bernoulli, llamado así por Jacob Bernoulli.
Considera el experimento de monedas con\(n = 4\), y Let\(Y\) denotar el número de cabezas.
- Dar el conjunto de resultados\(S\) en forma de lista.
- Dar el evento\(\{Y = k\}\) en forma de lista para cada uno\(k \in \{0, 1, 2, 3, 4\}\).
Contestar
Para simplificar la notación, representamos los resultados a cadenas de bits en lugar de secuencias ordenadas.
- \(S = \{1111, 1110, 1101, 1011, 0111, 1100, 1010, 1001, 0110, 0101, 0011, 1000, 0100, 0010, 0001, 0000\}\)
- \ begin {align}\ {Y = 0\} & =\ {0000\}\\ {Y = 1\} & =\ {1000, 0100, 0010, 0001\}\\ {Y = 2\} & =\ {1100, 1010, 1001, 0110, 0101, 0011\}\\ {Y = 3\} & =\ {1110, 1101, 1011, 111\}\\\ {Y = 4\} & =\ {1111\}\ final {alinear}
En la simulación del experimento de monedas, set\(n = 4\). Ejecute el experimento 100 veces y cuente el número de veces que\(\{Y = 2\}\) ocurre el evento.
Ahora considere el experimento general de la moneda con la moneda tirada\(n\) veces, y vamos a\(Y\) denotar el número de cabezas.
- Dar el conjunto de resultados\(S\) en forma de producto cartesiano, y dar la cardinalidad de\(S\).
- Expresar\(Y\) como una función en\(S\).
- Buscar\(\#\{Y = k\}\) (como un subconjunto de\(S\)) para\(k \in \{0, 1, \ldots, n\}\)
Contestar
- \(S = \{0, 1\}^n\)y\(\#(S) = 2^n\).
- \(Y(x_1, x_2, \ldots, x_n) = x_1 + x_2 + \cdots + x_n\). El conjunto de valores posibles es\(\{0, 1, \ldots, n\}\)
- \(\#\{Y = k\} = \binom{n}{k}\)
El experimento básico de dados consiste en lanzar dados\(k\) de\(n\) distintos lados (con caras numeradas del 1 al\(k\)) y registrar la secuencia de partituras\((X_1, X_2, \ldots, X_n)\). Este experimento es un ejemplo genérico de ensayos\(n\) multinomiales. El caso especial\(k = 6\) corresponde a dados estándar.
Considera el experimento de dados con dados\(n = 2\) estándar. Dejar\(S\) denotar el conjunto de resultados,\(A\) el evento de que la puntuación del primer dado es 1, y\(B\) el evento de que la suma de los puntajes es 7. Dar cada uno de los siguientes eventos en el formulario indicado:
- \(S\)en forma de producto cartesiano
- \(A\)en forma de lista
- \(B\)en forma de lista
- \(A \cup B\)en forma de lista
- \(A \cap B\)en forma de lista
- \(A^c \cap B^c\)en forma de predicado
Contestar
- \(S = \{1, 2, 3, 4, 5, 6\}^2\)
- \(A = \{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)\}\)
- \(B = \{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}\)
- \(A \cup B = \{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}\)
- \(A \cap B = \{(1,6)\}\)
- \(A^c \cap B^c = \{(x, y) \in S: x + y \ne 7 \text{ and } x \ne 1\}\)
En la simulación del experimento de dados, set\(n = 2\). Ejecute el experimento 100 veces y cuente el número de veces que ocurre cada evento en el ejercicio anterior.
Considera el experimento de dados con dados\(n = 2\) estándar, y deja\( S \) denotar el conjunto de resultados,\(Y\) la suma de las puntuaciones,\(U\) la puntuación mínima y\(V\) la puntuación máxima.
- Expresar\(Y\) como una función\( S \) y dar el conjunto de valores posibles en forma de lista.
- Expresar\(U\) como una función\( S \) y dar el conjunto de valores posibles en forma de lista.
- Expresar\(V\) como una función en el\( S \) y dar el conjunto de valores posibles en forma de lista.
- Dar el conjunto de valores posibles de\((U, V)\) en predicado de
Contestar
Tenga en cuenta que\( S = \{1, 2, 3, 4, 5, 6\}^2 \). Las siguientes funciones se definen en\( S \).
- \(Y(x_1, x_2) = x_1 + x_2\). El conjunto de valores es\(\{2, 3, \ldots, 12\}\)
- \(U(x_1, x_2) = \min\{x_1, x_2\}\). El conjunto de valores es\(\{1, 2, \ldots, 6\}\)
- \(V(x_1, x_2) = \max\{x_1, x_2\}\). El conjunto de valores es\(\{1, 2, \ldots, 6\}\)
- \(\left\{(u, v) \in \{1, 2, 3, 4, 5, 6\}^2: u \le v\right\}\)
Consideremos de nuevo el experimento de dados con dados\(n = 2\) estándar, y vamos a\( S \) denotar\(Y\) el conjunto de resultados, la suma de\(U\) las puntuaciones, la puntuación mínima y\(V\) la puntuación máxima. Dar cada uno de los siguientes como subconjuntos de\( S \), en forma de lista.
- \(\{X_1 \lt 3, X_2 \gt 4\}\)
- \(\{Y = 7\}\)
- \(\{U = 2\}\)
- \(\{V = 4\}\)
- \(\{U = V\}\)
Contestar
- \(\{(1,5), (2,5), (1,6), (2,6)\}\)
- \(\{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}\)
- \(\{(2,2), (2,3), (3,2), (2,4), (4,2), (2,5), (5,2), (2,6), (6,2)\}\)
- \(\{(4,1), (1,4), (2,4), (4,2), (4,3), (3,4), (4,4)\}\)
- \(\{(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)\}\)
En el experimento de dados, set\(n = 2\). Ejecutar el experimento 100 veces. Contar el número de veces que ocurrió cada evento en el ejercicio anterior.
En el experimento general de dados con dados\(n\) distintos\(k\) lados, vamos a\(Y\) denotar la suma de las puntuaciones,\(U\) la puntuación mínima y\(V\) la puntuación máxima.
- Dar el conjunto de resultados\( S \) y encontrar\( \#(S) \).
- Expresar\(Y\) como una función en\( S \), y dar el conjunto de valores posibles en forma de lista.
- Expresar\(U\) como una función en\( S \), y dar el conjunto de valores posibles en forma de lista.
- Expresar\(V\) como una función en\( S \), y dar el conjunto de valores posibles en forma de lista.
- Dar el conjunto de valores posibles de\((U, V)\) en predicado de.
Contestar
- \(S = \{1, 2, \ldots, k\}^n\)y\(\#(S) = k^n\)
- \(Y(x_1, x_2, \ldots, x_n) = x_1 + x_2 + \cdots + x_n\). El conjunto de valores posibles es\(\{n, n + 1, \ldots, n k\}\)
- \(U(x_1, x_2, \ldots, x_n) = \min\{x_1, x_2, \ldots, x_n\}\). El conjunto de valores posibles es\(\{1, 2, \ldots, k\}\).
- \(V(x_1, x_2, \ldots, x_n) = \max\{x_1, x_2 \ldots, x_n\}\). El conjunto de valores posibles es\(\{1, 2, \ldots, k\}\)
- \(\left\{(u, v) \in \{1, 2, \ldots, k\}^2: u \le v\right\}\)
El conjunto de resultados de un experimento aleatorio depende, por supuesto, de qué información se registra. El siguiente ejercicio es una ilustración.
Un experimento consiste en lanzar un par de dados estándar repetidamente hasta que la suma de las dos puntuaciones sea 5 o 7. Vamos a\(A\) denotar el evento de que la suma es 5 en lugar de 7 en el tiro final. Experimentos de este tipo surgen en los dados del juego de casino.
- Supongamos que se registra el par de puntajes en cada tirada. Definir el conjunto de resultados del experimento y describir\(A\) como un subconjunto de este conjunto.
- Supongamos que se registra el par de puntajes en el tiro final. Definir el conjunto de resultados del experimento y describir\(A\) como un subconjunto de este conjunto.
Contestar
Dejar\(D_5 = \{(1,4), (2,3), (3,2), (4,1)\}\),\(D_7 = \{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}\),\(D = D_5 \cup D_7 \), y\( C = D^c \)
- \(S = D \cup (C \times D) \cup (C^2 \times D) \cup \cdots\),\(A = D_5 \cup (C \times D_5) \cup (C^2 \times D_5) \cup \cdots\)
- \(S = D\),\(A = D_5\)
Supongamos que se tiran 3 dados estándar y\((X_1, X_2, X_3)\) se registra la secuencia de puntuaciones. Una persona paga $1 por jugar. Si algunos de los dados salen 6, entonces el jugador recibe su $1 de vuelta, más $1 por cada 6. De lo contrario pierde su $1. Vamos a\(W\) denotar las ganancias netas de la persona. Este es el juego de chuck-a-luck y se trata con más detalle en el capítulo de Juegos de azar.
- Dar el conjunto de resultados\(S\) en forma de producto cartesiano.
- Expresar\(W\) como una función\(S\) y dar el conjunto de valores posibles en forma de lista.
Contestar
- \(S = \{1, 2, 3, 4, 5, 6\}^3\)
- \(W(x_1, x_2, x_3) = \bs{1}\left(x_1 = 6\right) + \bs{1}\left(x_2 = 6\right) + \bs{1}\left(x_3 = 6\right) - \bs{1}\left(x_1 \ne 6, x_2 \ne 6, x_3 \ne 6\right)\). El conjunto de valores posibles es\(\{-1, 1, 2, 3\}\)
Juega varias veces al experimento de chuck-a-luck y mira cómo te va.
En el experimento de troquelado, se enrolla una matriz estándar y luego se lanza una moneda el número de veces que se muestra en la matriz. \(\bs{X}\)Se registra la secuencia de puntuaciones de monedas (0 para colas, 1 para cabezas). Dejar\(N\) denotar la puntuación del dado y\(Y\) el número de cabezas.
- Dar el conjunto de resultados\(S\) en términos de poderes cartesianos y encontrar\(\#(S)\).
- Expresar\(N\) como una función\(S\) y dar el conjunto de valores posibles en forma de lista.
- Expresar\(Y\) como una función\(S\) y dar el conjunto de valores posibles en forma de lista.
- Dar el evento de\(A\) que todos los tirados resulten en cabezas en forma de lista.
Contestar
- \(S = \bigcup_{n=1}^6 \{0, 1\}^n\),\(\#(S) = 126\)
- \(N(x_1, x_2, \ldots, x_n) = n\)para\((x_1, x_2, \ldots, x_n) \in S\). El conjunto de valores es\(\{1, 2, 3, 4, 5, 6\}\).
- \(Y(x_1, x_2, \ldots, x_n) = \sum_{i=1}^n x_i\)para\((x_1, x_2, \ldots, x_n) \in S\). El conjunto de valores posibles es\(\{0, 1, 2, 3, 4, 5, 6\}\).
- \(A = \{1, 11, 111, 1111, 11111, 111111\}\)
Ejecute la simulación del experimento die-coin 10 veces. Para cada ejecución, dar los valores de las variables aleatorias\(\bs{X}\)\(N\),, y\(Y\) del ejercicio anterior. Contar el número de veces que\(A\) ocurre el evento.
En el experimento de troqueles, tenemos una moneda y dos dados distintos, digamos uno rojo y otro verde. Primero se lanza la moneda, y luego si el resultado es cabezas se lanza el dado rojo, mientras que si el resultado es colas se lanza el dado verde. Se registra la puntuación de la moneda\(X\) y la puntuación del dado\(Y\) elegido. Supongamos ahora que el dado rojo es un dado estándar de 6 lados, y el troquel verde un dado de 4 lados.
- Dar el conjunto de resultados\(S\) en forma de lista.
- Expresar\(X\) como una función en\( S \).
- Expresar\(Y\) como una función en\( S \).
- Dar el evento\(\{Y \ge 3\}\) como un subconjunto de\( S \) en forma de lista.
Contestar
- \(\{(0,1), (0,2), (0,3), (0,4), (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)\}\)
- \(X(i, j) = i\)para\((i, j) \in S\)
- \(Y(i, j) = j\)para\((i, j) \in S\)
- \(\{(0,3), (0,4), (1,3), (1,4), (1,5), (1,6)\}\)
Ejecuta el experimento de troqueles de monedas 100 veces, con varios tipos de dados.
Modelos de Muestreo
Recordemos que muchos experimentos aleatorios pueden considerarse como experimentos de muestreo. Para el modelo general de muestreo finito, comenzamos con una población\(D\) con objetos\(m\) (distintos). Seleccionamos una muestra de\(n\) objetos de la población. Si el muestreo se realiza de manera aleatoria, entonces tenemos un experimento aleatorio con la muestra como resultado básico. Así, el conjunto de resultados del experimento es literalmente el conjunto de muestras; este es el origen histórico del término espacio muestral. Existen cuatro tipos comunes de muestreo de una población finita, con base en los criterios de orden y reemplazo. Recordemos los siguientes hechos de la sección sobre estructuras combinatorias:
Muestras de tamaño\( n \) elegidas de una población con\( m \) elementos.
- Si el muestreo es con reemplazo y con respecto al orden, entonces el conjunto de muestras es el poder cartesiano\(D^n\). El número de muestras es\(m^n\).
- Si el muestreo es sin reemplazo y con respecto al orden, entonces el conjunto de muestras es el conjunto de todas las permutaciones de tamaño\(n\) de\(D\). El número de muestras es\(m^{(n)} = m (m - 1) \cdots [m - (n - 1)]\).
- Si el muestreo es sin reemplazo y sin tener en cuenta el orden, entonces el conjunto de muestras es el conjunto de todas las combinaciones (o subconjuntos) de tamaño\(n\) de\(D\). El número de muestras es\(\binom{m}{n}\).
- Si el muestreo es con reemplazo y sin tener en cuenta el orden, entonces el conjunto de muestras es el conjunto de todos los multiconjuntos de tamaño\(n\) de\(D\). El número de muestras es\(\binom{m + n - 1}{n}\).
Si tomamos muestras con reemplazo, el tamaño de la muestra\(n\) puede ser cualquier entero positivo. Si tomamos muestras sin reemplazo, el tamaño de la muestra no puede exceder el tamaño de la población, por lo que debemos tener\(n \in \{1, 2, \ldots, m\}\).
Los experimentos básicos de monedas y dados son ejemplos de muestreo con reemplazo. Si tiramos una moneda\(n\) veces y registramos la secuencia de puntuaciones (donde como de costumbre, 0 denota colas y 1 denota cabezas), entonces generamos una muestra ordenada de tamaño\(n\) con reemplazo de la población\(\{0, 1\}\). Si lanzamos dados estándar\(n\) (distintos) y registramos la secuencia de puntuaciones, entonces generamos una muestra ordenada de tamaño\(n\) con reemplazo de la población\(\{1, 2, 3, 4, 5, 6\}\).
Supongamos que el muestreo es sin reemplazo (el caso más común). Si registramos la muestra ordenada\(\bs{X} = (X_1, X_2, \ldots, X_n)\), entonces la muestra desordenada\(\bs{W} = \{X_1, X_2, \ldots, X_n\}\) es una variable aleatoria (es decir, una función de\(\bs{X}\)). Por otro lado, si solo registramos la muestra desordenada\(\bs{W}\) en primer lugar, entonces no podemos recuperar la muestra pedida. Tenga en cuenta también que el número de muestras ordenadas de tamaño\(n\) es simplemente\(n!\) multiplicado por el número de muestras desordenadas de tamaño\(n\). No existe una relación tan simple cuando el muestreo es con reemplazo. Esto resultará ser un punto importante cuando estudiemos modelos de probabilidad basados en muestras aleatorias, en la siguiente sección.
Considerar una muestra de tamaño\(n = 3\) elegida sin reemplazo de la población\(\{a, b, c, d, e\}\).
- Give\(T\), el conjunto de muestras desordenadas en forma de lista.
- Dar en forma de lista el conjunto de todas las muestras ordenadas que corresponden a la muestra desordenada\(\{b, c, e\}\).
- Tenga en cuenta que por cada muestra desordenada, hay 6 muestras ordenadas.
- Dar la cardinalidad de\(S\), el conjunto de muestras ordenadas.
Contestar
- \(T = \left\{\{a,b,c\}, \{a,b,d\}, \{a,b,e\}, \{a,c,d\}, \{a,c,e\}, \{a,d,e\}, \{b,c,d\}, \{b,c,e\}, \{b,d,e\}, \{c,d,e\}\right\}\)
- \(\{(b,c,e), (b,e,c), (c,b,e), (c,e,b), (e,b,c), (e,c,b)\}\)
- 60
Tradicionalmente en la teoría de la probabilidad, una urna que contiene bolas se utiliza a menudo como metáfora para una población finita.
Supongamos que una urna contiene 50 bolas (distintas). Se selecciona una muestra de 10 bolas de la urna. Encuentra el número de muestras en cada uno de los siguientes casos:
- Muestras ordenadas con reemplazo
- Muestras pedidas sin reemplazo
- Muestras desordenadas sin reemplazo
- Muestras desordenadas con reemplazo
Contestar
- \(97\,656\,250\,000\,000\,000\)
- \(37\,276\,043\,023\,296\,000\)
- \(10\,272\,278\,170\)
- \(62\,828\,356\,305\)
Supongamos nuevamente que tenemos una población\(D\) con objetos\(m\) (distintos), pero supongamos ahora que cada objeto es uno de dos tipos, ya sea tipo 1 o tipo 0. Se dice que tales poblaciones son dicotómicas. Aquí hay algunos ejemplos específicos:
- La población está compuesta por personas, cada una de ellas masculinas o femeninas.
- La población está formada por votantes, cada uno demócrata o republicano.
- La población consiste en dispositivos, cada uno bien o defectuoso.
- La población consiste en bolas, cada una roja o verde.
Supongamos que la población\(D\) tiene objetos\(r\) tipo 1 y por lo tanto\(m - r\) escribe 0 objetos. Por supuesto, debemos tener\(r \in \{0, 1, \ldots, m\}\). Ahora supongamos que seleccionamos una muestra de tamaño\(n\) sin reemplazo de la población. Tenga en cuenta que este modelo tiene tres parámetros: el tamaño de la población\(m\), el número de objetos tipo 1 en la población\(r\) y el tamaño de la muestra\(n\).
Dejar\(Y\) denotar el número de objetos tipo 1 en la muestra. Entonces
- \(\#\{Y = k\} = \binom{n}{k} r^{(k)} (m - r)^{(n - k)}\)para cada uno\(k \in \{0, 1, \ldots, n\}\), si el evento es considerado como un subconjunto de\(S\), el conjunto de muestras ordenadas.
- \(\#\{Y = k\} = \binom{r}{k} \binom{m - r}{n - k}\)para cada uno\(k \in \{0, 1, \ldots, n\}\), si el evento es considerado como un subconjunto de\(T\), el conjunto de muestras desordenadas.
- La expresión en (a) es\(n!\) veces la expresión en (b).
Prueba
- \(\binom{n}{k}\)es el número de formas de seleccionar las coordenadas (en la muestra ordenada) donde irán los objetos tipo 1,\(r^{(k)}\) es el número de formas de seleccionar una permutación de objetos\(k\) tipo 1, y\((m - r)^{(n-k)}\) es el número de formas de seleccionar una permutación de objetos\(n - k\) tipo 0. El resultado se desprende del principio de multiplicación.
- \(\binom{r}{k}\)es el número de formas de seleccionar una combatición de objetos\(k\) tipo 1 y\(\binom{m - r}{n - k}\) es el número de formas de seleccionar una combinación de objetos\(n - k\) tipo 0. El resultado se desprende nuevamente del principio de multiplicación.
- Este resultado se puede mostrar algebraicamente, pero un argumento combinatorio es mejor. Por cada combinación de tamaño\(n\) hay\(n!\) permutaciones de esos objetos.
Un lote de 50 componentes consta de 40 componentes buenos y 10 componentes defectuosos. Se selecciona una muestra de 5 componentes, sin reemplazo. Dejar\(Y\) denotar el número de defectivos en la muestra.
- Dejar\(S\) denotar el conjunto de muestras ordenadas. Encontrar\(\#(S)\).
- Dejar\(T\) denotar el conjunto de muestras desordenadas. Encontrar\(\#(T)\).
- Como subconjunto de\(T\), encontrar\(\#\{Y = k\}\) para cada uno\(k \in \{0, 1, 2, 3, 4, 5\}\).
Contestar
- \(254\,251\,200\)
- \(2\,118\,760\)
- \(\#\{Y = 0\} = 658\,008\),\(\#\{Y = 1\} = 913\,900\)\(\#\{Y = 2\} = 444\,600\),\(\#\{Y = 3\} = 93\,600\),\(\#\{Y = 4\} = 8\,400\),\(\#\{Y = 5\} = 252\)
Ejecuta la simulación del experimento de bola y urna 100 veces para los valores de los parámetros en el último ejercicio:\( m = 50 \),\( r = 10 \),\( n = 5 \). Anote los valores de la variable aleatoria\(Y\).
Tarjetas
Recordemos que una baraja de cartas estándar puede ser modelada por el conjunto de productos cartesianos\[D = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, j, q, k\} \times \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\}\] donde la primera coordenada codifica la denominación o tipo (as, 2—10, jack, reina, rey) y donde la segunda coordenada codifica el palo (palos, diamantes, corazones, espadas). A veces representamos una carta como una cadena en lugar de un par ordenado (por ejemplo\(q \heartsuit\) más que\((q, \heartsuit)\) para la reina de corazones).
La mayoría de los juegos de cartas implican muestreo sin reemplazo de la baraja\(D\), que juega el papel de la población. Así, el experimento básico de cartas consiste en repartir\(n\) cartas de un mazo estándar sin reemplazo; en este contexto especial, la muestra de cartas a menudo se conoce como una mano. Al igual que en el modelo de muestreo general, si registramos la mano ordenada\(\bs{X} = (X_1, X_2, \ldots, X_n)\), entonces la mano desordenada\(\bs{W} = \{X_1, X_2, \ldots, X_n\}\) es una variable aleatoria (es decir, una función de\(\bs{X}\)). Por otro lado, si acabamos de registrar la mano desordenada\(\bs{W}\) en primer lugar, entonces no podemos recuperar la mano ordenada. Por último, recordemos que\(n = 5\) es el experimento del póker y\(n = 13\) es el experimento del puente. El juego de póquer se trata con más detalle en el capítulo de Juegos de azar.
Supongamos que una sola carta se reparte desde una baraja estándar. Dejar\(Q\) denotar el evento de que la tarjeta es una reina y\(H\) el evento de que la tarjeta es un corazón. Dar cada uno de los siguientes eventos en forma de lista:
- \(Q\)
- \(H\)
- \(Q \cup H\)
- \(Q \cap H\)
- \(Q \setminus H\)
Contestar
- \(Q = \{q \clubsuit, q \diamondsuit, q \heartsuit, q \spadesuit\}\)
- \(H = \{1 \heartsuit, 2 \heartsuit, \ldots, 10 \heartsuit, j \heartsuit, q \heartsuit, k \heartsuit\}\)
- \(Q \cup H = \{1 \heartsuit, 2 \heartsuit, \ldots, 10 \heartsuit, j \heartsuit, q \heartsuit, k \heartsuit, q \clubsuit, q \diamondsuit, q \spadesuit\}\)
- \(Q \cap H = \{q \heartsuit\}\)
- \(Q \setminus H = \{q \clubsuit, q \diamondsuit, q \spadesuit\}\)
En el experimento de cartas, set\(n = 1\). Ejecute el experimento 100 veces y cuente el número de veces que ocurre cada evento en el ejercicio anterior.
Supongamos que se reparten dos cartas de una baraja estándar y se registra la secuencia de cartas. Dejar\( S \) denotar el conjunto de resultados, y dejar\(Q_i\) denotar el evento de que la carta\(i\) th es una reina y\(H_i\) el evento para el que la carta\(i\) th es un corazón para\(i \in \{1, 2\}\). Encuentra el número de resultados en cada uno de los siguientes eventos:
- \(S\)
- \(H_1\)
- \(H_2\)
- \(H_1 \cap H_2\)
- \(Q_1 \cap H_1\)
- \(Q_1 \cap H_2\)
- \(H_1 \cup H_2\)
Contestar
- 2652
- 663
- 663
- 156
- 51
- 51
- 1170
Considera el experimento general de cartas en el que\(n\) las cartas se reparten desde una baraja estándar, y\(\bs{X}\) se registra la mano ordenada.
- Dar cardinalidad de\(S\), el conjunto de valores de la mano ordenada\( \bs{X} \).
- Dar la cardinalidad de\(T\), el conjunto de valores de la mano desordenada\(\bs{W}\).
- ¿Cuántas manos ordenadas corresponden a una mano desordenada dada?
- Calcular explícitamente los números en (a) y (b) when\(n = 5\) (poker).
- Calcular explícitamente los números en (a) y (b) when\(n = 13\) (bridge).
Contestar
- \(\#(S) = 52^{(n)}\)
- \(\#(T) = \binom{52}{n}\)
- \(n!\)
- \(311\,875\,200\),\(2\,598\,960\)
- \(3\,954\,242\,643\,911\,239\,680\,000\),\(635\,013\,559\,600\)
Considera el experimento puente de repartir 13 cartas de una baraja y grabar la mano desordenada. En el sistema de conteo de puntos más común, un as vale 4 puntos, un rey 3 puntos, una reina 2 puntos, y un jack 1 punto. Las otras tarjetas valen 0 puntos. Dejar\( S \) denotar el conjunto de resultados del experimento y\(V\) el valor puntual de la mano.
- Encuentra el conjunto de valores posibles de\(V\).
- Encuentra la cardinalidad del evento\(\{V = 0\}\) como un subconjunto de\( S \).
Contestar
- \(\{0, 1, \ldots, 37\}\)
- \(\#\{V = 0\} = 2\,310\,789\,600\)
En el experimento de cartas, establece\(n = 13\) y ejecuta el experimento 100 veces. Para cada ejecución, calcule el valor de cada una de las variables aleatorias\(V\) en el ejercicio anterior.
Considera el experimento de poker de repartir 5 cartas de una baraja. Encuentra la cardinalidad de cada uno de los eventos a continuación, como un subconjunto del conjunto de manos desordenadas.
- \(A\): el evento de que la mano es una casa llena (3 tarjetas de un tipo y 2 de otro tipo).
- \(B\): el evento de que la mano tenga 4 de un tipo (4 cartas de un tipo y 1 de otro tipo).
- \(C\): el caso de que todas las cartas de la mano estén en el mismo palo (la mano está a ras o a ras recta).
Contestar
- \(\#(A) = 3744\)
- \(\#(B) = 624\)
- \(\#(C) = 5148\)
Ejecuta el experimento de poker 1000 veces. Anote el número de veces que ocurrieron los hechos\(A\)\(B\),, y\(C\) en el ejercicio anterior.
Considera el experimento puente de repartir 13 cartas de una baraja estándar. Dejar\( S \) denotar el conjunto de manos desordenadas,\(Y\) el número de corazones en la mano, y\(Z\) el número de reinas en la mano.
- Encuentra la cardinalidad del evento\(\{Y = y\}\) como un subconjunto de\( S \) para cada uno\(y \in \{0, 1, \ldots, 13\}\).
- Encuentra la cardinalidad del evento\(\{Z = z\}\) como un subconjunto de\( S \) para cada uno\(z \in \{0, 1, 2, 3, 4\}\).
Contestar
- \(\#(Y = y) = \binom{13}{y} \binom{39}{13 - y}\)para\(y \in \{0, 1, \ldots, 13\}\)
- \(\#(Z = z) = \binom{4}{z} \binom{48}{4 - z}\)para\(z \in \{0, 1, 2, 3, 4\}\)
Modelos Geométricos
En los experimentos que hemos considerado hasta ahora, los espacios muestrales han sido todos discretos (de manera que el conjunto de resultados es finito o contablemente infinito). En esta subsección, consideramos espacios de muestra euclidianos donde el conjunto de resultados\(S\) es continuo en un sentido que dejaremos claro más adelante. Los experimentos que consideramos a veces se denominan modelos geométricos porque implican seleccionar un punto al azar de un conjunto euclidiano.
Primero consideramos el experimento de monedas de Buffon, que consiste en lanzar una moneda con radio\(r \le \frac{1}{2}\) al azar sobre un piso cubierto con azulejos cuadrados de longitud lateral 1. Las coordenadas\((X, Y)\) del centro de la moneda se registran con relación a los ejes a través del centro del cuadrado en el que aterriza la moneda. Los experimentos de Buffon se estudian con más detalle en el capítulo sobre Modelos Geométricos y llevan el nombre de Compte de Buffon
En el experimento de la moneda de Buffon, vamos a\( S \) denotar\(A\) el conjunto de resultados, el evento de que la moneda no toque los lados del cuadrado, y dejar\(Z\) denotar la distancia desde el centro de la moneda hasta el centro del cuadrado.
- Describir\(S\) como un producto cartesiano.
- Describir\(A\) como un subconjunto de\(S\).
- Describir\(A^c\) como un subconjunto de\(S\).
- Expresar\(Z\) como una función en\(S\).
- Expresar el evento\(\{X \lt Y\}\) como un subconjunto de\(S\).
- Expresar el evento\(\left\{Z \leq \frac{1}{2}\right\}\) como un subconjunto de\(S\).
Contestar
- \(S = \left[-\frac{1}{2}, \frac{1}{2}\right]^2\)
- \(A = \left[r - \frac{1}{2}, \frac{1}{2} - r\right]^2\)
- \(A^c = \left\{(x, y) \in S: x \lt r - \frac{1}{2} \text{ or } x \gt \frac{1}{2} - r \text{ or } y \lt r - \frac{1}{2} \text{ or } y \gt \frac{1}{2} - r\right\}\)
- \(Z(x, y) = \sqrt{x^2 + y^2}\)para\((x, y) \in S\)
- \(\{X \lt Y\} = \{(x, y) \in S: x \lt y\}\)
- \(\{Z \lt \frac{1}{2}\} = \left\{(x, y) \in S: x^2 + y^2 \lt \frac{1}{4}\right\}\)
Ejecuta el experimento de monedas de Buffon 100 veces con\(r = 0.2\). Para cada ejecución, anote si\(A\) se produce el evento y calcule el valor de la variable aleatoria\(Z\).
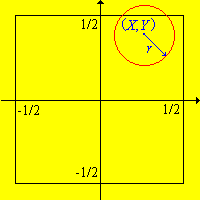
\((X, Y)\)Se elige un punto al azar en la región circular de radio 1 en\(\R^2\) centrado en el origen. Vamos a\(S\) denotar el conjunto de resultados. Dejar\(A\) denotar el evento de que el punto se encuentra en la región cuadrada inscrita centrada en el origen, con lados paralelos a los ejes de coordenadas. Dejar\(B\) denotar el evento de que el punto está en el cuadrado inscrito con vértices\((\pm 1, 0)\),\((0, \pm 1)\).
- Describir\(S\) matemáticamente y bosquejar el conjunto.
- Describir\(A\) matemáticamente y bosquejar el conjunto.
- Describir\(B\) matemáticamente y bosquejar el conjunto.
- Sketch\(A \cup B\)
- Sketch\(A \cap B\)
- Sketch\(A \cap B^c\)
Contestar
- \(S = \left\{(x, y): x^2 + y^2 \le 1\right\}\)
- \(A = \left\{(x, y): -\frac{1}{\sqrt{2}} \le x \le \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \le y \le \frac{1}{\sqrt{2}}\right\}\)
- \(B = \left\{(x, y) \in S: -1 \le \left|x + y\right| \le 1, -1 \le \left|y - x\right| \le 1\right\}\)
Confiabilidad
En el modelo simple de confiabilidad estructural, un sistema está compuesto por\(n\) componentes, cada uno de los cuales está funcionando o falló. El estado del componente\(i\) es una variable aleatoria indicadora\(X_i\), donde 1 significa trabajar y 0 significa falla. Así,\(\bs{X} = (X_1, X_2, \ldots, X_n)\) es un vector de variables aleatorias indicadoras que especifica los estados de todos los componentes, y por lo tanto el conjunto de resultados del experimento lo es\(S = \{0, 1\}^n\). El sistema en su conjunto también está funcionando o falló, dependiendo únicamente de los estados de los componentes y de cómo los componentes estén conectados entre sí. Así, el estado del sistema es también una variable aleatoria indicadora y es una función de\( \bs X \). El estado del sistema (funcionando o fallido) en función de los estados de los componentes es la función de estructura.
Un sistema en serie está funcionando si y solo si cada componente está funcionando. El estado del sistema es\[U = X_1 X_2 \cdots X_n = \min\left\{X_1, X_2, \ldots, X_n\right\}\]
Un sistema paralelo está funcionando si y solo si al menos un componente está funcionando. El estado del sistema es\[V = 1 - \left(1 - X_1\right)\left(1 - X_2\right) \cdots \left(1 - X_n\right) = \max\left\{X_1, X_2, \ldots, X_n\right\}\]
De manera más general, un \(n\)sistema\(k\) fuera del sistema está funcionando si y solo si al menos\(k\) de los\(n\) componentes están funcionando. Tenga en cuenta que un sistema paralelo es un 1 fuera del\(n\) sistema y un sistema en serie es un sistema\(n\) fuera de\(n\) sistema. Un sistema\(k\) fuera de\(2 k\) sistema es un sistema de reglas mayoritarias.
El estado de la\(k\) fuera del\(n\) sistema es\( U_{n,k} = \bs 1\left(\sum_{i=1}^n X_i \ge k\right) \). La función de estructura también se puede expresar como un polinomio en las variables.
Dar explícitamente el estado del sistema de\(k\) fuera de 3, como una función polinómica de los estados componentes\((X_1, X_2, X_3)\), para cada uno\(k \in \{1, 2, 3\}\).
Contestar
- \(U_{3,1} = X_1 + X_2 + X_3 - X_1 X_2 - X_1 X_3 - X_2 X_3 + X_1 X_2 X_3\)
- \(U_{3,2} = X_1 X_2 + X_1 X_3 + X_2 X_3 - 2 \, X_1 X_2 X_3\)
- \(U_{3,3} = X_1 X_2 X_3\)
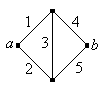
En algunos casos, el sistema puede representarse como una gráfica o red. Los bordes representan los componentes y los vértices las conexiones entre los componentes. El sistema funciona si y sólo si hay una ruta de trabajo entre dos vértices designados, que denotaremos por\(a\) y\(b\).
Encuentre el estado de la red de puentes de Wheatstone que se muestra a continuación, en función de los estados de los componentes. La red lleva el nombre de Charles Wheatstone.
Contestar
No todas las funciones tienen\(u: \{0, 1\}^n \to \{0, 1\}\) sentido como función estructural. Explique por qué las siguientes propiedades podrían ser deseables:
- \(u(0, 0, \ldots, 0) = 0\)y\(s(1, 1, \ldots, 1) = 1\)
- \(u\)es una función creciente, donde\(\{0, 1\}\) se le da el orden ordinario y\(\{0, 1\}^n\) el orden de producto correspondiente.
- Para cada uno\(i \in \{1, 2, \ldots, n\}\), existen\(\bs{x}\) y\(\bs{y}\) en\(\{0, 1\}^n\) todas cuyas coordenadas coinciden, excepto\(x_i = 0\) y\(y_i = 1\), y\(u(\bs{x}) = 0\) mientras\(u(\bs{y}) = 1\).
Contestar
- Esto significa que si todos los componentes han fallado entonces el sistema ha fallado, y si todos los componentes están funcionando entonces el sistema está funcionando.
- Esto significa que si un componente en particular se cambia de falla a funcionar, entonces el sistema también puede pasar de fallar a funcionar, pero no de funcionar a fallar. Es decir, el sistema sólo puede mejorar.
- Esto significa que cada componente es relevante para el sistema, es decir, existe una configuración en la que el cambio\(i\) de componente de fallido a trabajo cambia el sistema de falla a funcionar.
El modelo que se acaba de discutir es un modelo estático. Podemos extenderlo a un modelo dinámico asumiendo que ese componente\(i\) está funcionando inicialmente, pero tiene un tiempo aleatorio para fallar\(T_i\), tomando valores\([0, \infty)\), para cada uno\(i \in \{1, 2, \ldots, n\}\). Así, el resultado básico del experimento es el vector aleatorio de tiempos de falla\((T_1, T_2, \ldots, T_n)\), y así lo es el conjunto de resultados\([0, \infty)^n\).
Considerar el modelo de confiabilidad dinámica para un sistema con función de estructura\(u\) (válido en el sentido del ejercicio anterior).
- El estado del componente\(i\) en el momento\(t \ge 0\) es\(X_i(t) = \bs{1}\left(T_i \gt t\right)\).
- El estado del sistema en el momento\(t\) es\(X(t) = s\left[X_1(t), X_2(t), \ldots, X_n(t)\right]\).
- El tiempo de falla del sistema es\(T = \min\{t \ge 0: X(t) = 0\}\).
Supongamos que tenemos dos dispositivos y que grabamos\((X, Y)\), donde\(X\) está el tiempo de falla del dispositivo 1 y\(Y\) es el tiempo de falla del dispositivo 2. Ambas variables toman valores en el intervalo\([0, \infty)\), donde las unidades están en cientos de horas. Esboce cada uno de los siguientes eventos:
- El conjunto de resultados\(S\)
- \(\{X \lt Y\}\)
- \(\{X + Y \gt 2\}\)
Contestar
- \( S = [0, \infty)^2 \), el primer cuadrante del plano de coordenadas.
- \( \{X \lt Y\} = \{(x, y) \in S: x \lt y\} \). Esta es la región por debajo de la línea diagonal\( x = y \).
- \( \{X + Y \gt 2\} = \{(x, y) \in S: x + y \gt 2 \). Esta es la región arriba (o a la derecha) de la línea\( x + y = 2 \).
Genética
Por favor refiérase a la discusión de genética en la sección de experimentos aleatorios si necesita revisar algunas de las definiciones de esta sección.
Recordemos primero que el tipo de sangre ABO en humanos está determinado por tres alelos:\(a\),\(b\), y\(o\). Además,\(o\) es recesivo y\(a\) y\(b\) son codominantes.
Supongamos que una persona es elegida al azar y se registra su genotipo. Dar cada uno de los siguientes en forma de lista.
- El conjunto de resultados S
- El evento que la persona es tipo\(A\)
- El evento que la persona es tipo\(B\)
- El evento que la persona es tipo\(AB\)
- El evento que la persona es tipo\(O\)
Contestar
- \(S = \{aa, ab, ao, bb, bo, oo\}\)
- \(A = \{aa, ao\}\)
- \(B = \{bb, bo\}\)
- \(AB = \{ab\}\)
- \(O = \{oo\}\)
Supongamos a continuación que el color de la vaina en cierto tipo de planta de guisante está determinado por un gen con dos alelos:\(g\) para el verde y\(y\) para el amarillo, y que\(g\) es dominante.
Supongamos que se recolectan plantas de guisante\(n\) (distintas) y se registra la secuencia de genotipos de color de vaina.
- Dar el conjunto de resultados\(S\) en forma de producto cartesiano y encontrar\(\#(S)\).
- Dejar\(N\) denotar el número de plantas con vainas verdes. Buscar\(\#(N = k)\) (como un subconjunto de\( S \)) para cada uno\(k \in \{0, 1, \ldots, n\}\).
Contestar
- \(S = \{gg, gy, yy\}^n \),\(\#(S) = 3^n\)
- \(\binom{n}{k} 2^k\)
A continuación, considere un trastorno hereditario vinculado al sexo en humanos (como el daltonismo o la hemofilia). Dejar\(h\) denotar el alelo sano y\(d\) el alelo defectuoso para el gen vinculado al trastorno. Recordemos que\(d\) es recesivo para las mujeres.
Supongamos que\(n\) las mujeres son muestreadas y se registra la secuencia de genotipos.
- Dar el conjunto de resultados\(S\) en forma de producto cartesiano y encontrar\(\#(S)\).
- Vamos a\(N\) denotar el número de mujeres que están completamente sanas (genotipo\(hh\)). Buscar\(\#(N = k)\) (como un subconjunto de\( S \)) para cada uno\(k \in \{0, 1, \ldots, n\}\).
Contestar
- \(S = \{hh, hd, dd\}^n\),\(\#(S) = 3^n\)
- \(\binom{n}{k} 2^{n-k}\)
Emisiones radiactivas
La emisión de partículas elementales de una muestra de material radiactivo se produce de manera aleatoria. Supongamos que el tiempo de emisión de la partícula\(i\) th es una variable aleatoria\(T_i\) tomando valores en\((0, \infty)\). Si medimos estos tiempos de llegada, entonces el vector de resultado básico es\((T_1, T_2, \ldots)\) y así lo es el conjunto de resultados\(S = \{(t_1, t_2, \ldots): 0 \lt t_1 \lt t_2 \lt \cdots\}\).
Ejecutar la simulación del experimento gamma en modo de un solo paso para diferentes valores de los parámetros. Observe los horarios de llegada.
Ahora vamos a\(N_t\) denotar el número de emisiones en el intervalo\((0, t]\). Entonces
- \(N_t = \max\left\{n \in \N_+: T_n \le t\right\}\).
- \(N_t \ge n\)si y sólo si\(T_n \le t\).
Ejecute la simulación del experimento de Poisson en modo de un solo paso para diferentes valores de parámetros. Observe las llegadas en el intervalo de tiempo especificado.
Experimentos estadísticos
En el experimento básico de cigarras, se captura una cigarra en el área de Middle Tennessee y se registran las siguientes medidas: peso corporal (en gramos), longitud del ala, ancho del ala y longitud corporal (en milímetros), tipo de especie y género. El conjunto de datos de cigarra da los resultados de 104 repeticiones de este experimento.
- Definir el conjunto de resultados\( S \) para el experimento básico.
- Que\(F\) sea el evento de que una cigarra sea femenina. Describir\(F\) como un subconjunto de\( S \). Determinar si\(F\) ocurre por cada cigarra en el conjunto de datos.
- Dejar\(V\) denotar la relación entre la longitud del ala y el ancho del ala. Compute\(V\) para cada cigarra.
- Dar el conjunto de resultados para el experimento compuesto que consta de 104 repeticiones del experimento básico.
Contestar
Para el género, digamos 0 denotar hembra y 1 macho, para especies, dejar 1 denotar tredecula, 2 tredecim y 3 tredecassini.
- \(S = (0, \infty)^4 \times \{0, 1\} \times \{1, 2, 3\}\)
- \(F = \{(x_1, x_2, x_3, x_4, y, z) \in S: y = 0\}\)
- \(S^{104}\)
En el experimento básico de M&M, se compra una bolsa de M&Ms (de un tamaño especificado) y se registran las siguientes medidas: el número de caramelos rojos, verdes, azules, amarillos, naranjas y marrones, y el peso neto (en gramos). El conjunto de datos de M&M da los resultados de 30 repeticiones de este experimento.
- Definir el conjunto de resultados\( S \) para el experimento básico.
- Que\(A\) sea el evento de que una bolsa contenga al menos 57 caramelos. Describir\(A\) como un subconjunto de\( S \).
- Determinar si\(A\) ocurre por cada bolsa en el conjunto de datos.
- Dejar\(N\) denotar el número total de caramelos. Calcular\(N\) para cada bolsa en el conjunto de datos.
- Dar el conjunto de resultados para el experimento compuesto que consta de 30 repeticiones del experimento básico.
Contestar
- \(S = \N^6 \times (0, \infty)\)
- \(A = \{(n_1, n_2, n_3, n_4, n_5, n_6, w) \in S: n_1 + n_2 + \cdots + n_6 \gt 57\}\)
- \(S^{30}\)


