4.2: Propiedades adicionales
- Page ID
- 151944
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección, estudiamos algunas propiedades de valor esperado que son un poco más especializadas que las propiedades básicas consideradas en la sección anterior. Sin embargo, los nuevos resultados también son muy importantes. Incluyen dos desigualdades fundamentales así como fórmulas especiales para el valor esperado de una variable no negativa. Como es habitual, a menos que se indique lo contrario, suponemos que existen los valores esperados referenciados.
Teoría Básica
Desigualdad de Markov
Nuestro primer resultado se conoce como la desigualdad de Markov (que lleva el nombre de Andrei Markov). Da un límite superior para la probabilidad de cola de una variable aleatoria no negativa en términos del valor esperado de la variable.
Si\(X\) es una variable aleatoria no negativa, entonces\[ \P(X \ge x) \le \frac{\E(X)}{x}, \quad x \gt 0 \]
Prueba
Para\( x \gt 0 \), tenga en cuenta que\(x \cdot \bs{1}(X \ge x) \le X\). Tomando valores esperados a través de esta desigualdad da\(x \P(X \ge x) \le \E(X)\).
El límite superior en la desigualdad de Markov puede ser bastante crudo. De hecho, es muy posible que\( \E(X) \big/ x \ge 1 \), en cuyo caso el encuadernado carece de valor. Sin embargo, el valor real de la desigualdad de Markov radica en el hecho de que sostiene sin ninguna suposición alguna sobre la distribución de\( X \) (que no\( X \) sea negativa). También, como muestra un ejemplo a continuación, la desigualdad es apretada en el sentido de que la igualdad puede aguantar para un dado\( x \). Aquí hay un simple corolario de la desigualdad de Markov.
Si\( X \) es una variable aleatoria de valor real y\( k \in (0, \infty) \) luego\[ \P(\left|X\right| \ge x) \le \frac{\E\left(\left|X\right|^k\right)}{x^k} \quad x \gt 0 \]
Prueba
Ya que\( k \ge 0 \), la función\( x \mapsto x^k \) está aumentando estrictamente en\( [0, \infty) \). Por lo tanto, utilizando la desigualdad de Markov,\[ \P(\left|X\right| \ge x) = \P\left(\left|X\right|^k \ge x^k\right) \le \frac{\E\left(\left|X\right|^k\right)}{x^k} \]
En este corolario de la desigualdad de Markov, podríamos tratar de encontrar\( k \gt 0 \) para que\( \E\left( \left|X\right|^k\right) \big/ x^k \) se minimice, dando así el límite más apretado\( \P\left(\left|X\right|\right) \ge x)\).
Función de distribución derecha
Nuestros siguientes resultados dan formas alternativas de calcular el valor esperado de una variable aleatoria no negativa por medio de la función de distribución de cola derecha. Esta función también conocida como la función de confiabilidad si la variable representa la vida útil de un dispositivo.
Si\(X\) es una variable aleatoria no negativa entonces\[ \E(X) = \int_0^\infty \P(X \gt x) \, dx \]
Prueba
Una prueba se puede construir expresando\(\P(X \gt x)\) en términos de la función de densidad de probabilidad de\(X\), como una suma en el caso discreto o una integral en el caso continuo. Luego en la expresión\( \int_0^\infty \P(X \gt x) \, dx \) intercambiar la integral y la suma (en el caso discreto) o las dos integrales (en el caso continuo). Hay una prueba mucho más elegante si utilizamos el hecho de que podemos intercambiar valores esperados e integrales cuando el integrando no es negativo:\[ \int_0^\infty \P(X \gt x) \, dx = \int_0^\infty \E\left[\bs{1}(X \gt x)\right] \, dx = \E \left(\int_0^\infty \bs{1}(X \gt x) \, dx \right) = \E\left( \int_0^X 1 \, dx \right) = \E(X) \] Este intercambio es un caso especial del teorema de Fubini, llamado así por el matemático italiano Guido Fubini. Consulte la sección avanzada sobre el valor esperado como integral para obtener más detalles.
Aquí hay un resultado un poco más general:
Si\( X \) es una variable aleatoria no negativa y\( k \in (0, \infty) \) luego\[ \E(X^k) = \int_0^\infty k x^{k-1} \P(X \gt x) \, dx \]
Prueba
La misma prueba básica funciona:\[ \int_0^\infty k x^{k-1} \P(X \gt x) \, dx = \int_0^\infty k x^{k-1} \E\left[\bs{1}(X \gt x)\right] \, dx = \E \left(\int_0^\infty k x^{k-1} \bs{1}(X \gt x) \, dx \right) = \E\left( \int_0^X k x^{k-1} \, dx \right) = \E(X^k) \]
El siguiente resultado es similar al teorema anterior, pero está especializado en variables de valor entero no negativas:
Supongamos que\(N\) tiene una distribución discreta, tomando valores adentro\(\N\). Entonces\[ \E(N) = \sum_{n=0}^\infty \P(N \gt n) = \sum_{n=1}^\infty \P(N \ge n) \]
Prueba
Primero, las dos sumas de la derecha son equivalentes por un simple cambio de variables. Una prueba se puede construir expresando\(\P(N \gt n)\) como una suma en términos de la función de densidad de probabilidad de\(N\). Después en la expresión\( \sum_{n=0}^\infty \P(N \gt n) \) intercambiar las dos sumas. Aquí hay una prueba más elegante:\[ \sum_{n=1}^\infty \P(N \ge n) = \sum_{n=1}^\infty \E\left[\bs{1}(N \ge n)\right] = \E\left(\sum_{n=1}^\infty \bs{1}(N \ge n) \right) = \E\left(\sum_{n=1}^N 1 \right) = \E(N) \] Este intercambio es un caso especial de una regla general que permite el intercambio de valor esperado y una serie infinita, cuando los términos son no negativos. Consulte la sección avanzada sobre el valor esperado como integral para obtener más detalles.
Una definición general
La fórmula de valor esperado especial para variables no negativas puede ser utilizada como base de una formulación general de valor esperado que funcionaría para distribuciones discretas, continuas o incluso mixtas, y no requeriría el supuesto de la existencia de funciones de densidad de probabilidad. En primer lugar, se toma la fórmula especial como definición de\(\E(X)\) si no\(X\) es negativa.
Si\( X \) es una variable aleatoria no negativa, defina\[ \E(X) = \int_0^\infty \P(X \gt x) \, dx \]
A continuación, para\(x \in \R\), recordemos que las partes positivas y negativas de\(x\) son\( x^+ = \max\{x, 0\}\) y\(x^- = \max\{0, -x\} \).
Para\(x \in \R\),
- \(x^+ \ge 0\),\(x^- \ge 0\)
- \(x = x^+ - x^-\)
- \(\left|x\right| = x^+ + x^-\)
Ahora bien, si\(X\) es una variable aleatoria de valor real, entonces\(X^+\) y\(X^-\), las partes positiva y negativa de\(X\), son variables aleatorias no negativas, por lo que sus valores esperados se definen como arriba. La definición de\( \E(X) \) es entonces natural, anticipando por supuesto la propiedad de linealidad.
Si\( X \) es una variable aleatoria de valor real, defina\(\E(X) = \E\left(X^+\right) - \E\left(X^-\right)\), asumiendo que al menos uno de los valores esperados a la derecha es finito.
Las fórmulas habituales para el valor esperado en términos de la función de densidad de probabilidad, para distribuciones discretas, continuas o mixtas, ahora se probarían como teoremas. No vamos a ir más allá en esta dirección, sin embargo, ya que la definición más completa y general del valor esperado se da en la sección avanzada sobre el valor esperado como integral.
Teorema del Cambio de Variables
Supongamos que\( X \) toma valores\( S \) y tiene función de densidad de probabilidad\( f \). Supongamos también eso\( r: S \to \R \), así que esa\( r(X) \) es una variable aleatoria de valor real. El teorema del cambio de variables da una fórmula para la computación\( \E\left[r(X)\right] \) sin tener que encontrar primero la función de densidad de probabilidad de\( r(X) \). Si\( S \) es contable, entonces eso\( X \) tiene una distribución discreta, entonces\[ \E\left[r(X)\right] = \sum_{x \in S} r(x) f(x) \] If\( S \subseteq \R^n \) y\( X \) tiene una distribución continua en\( S \) entonces\[ \E\left[r(X)\right] = \int_S r(x) f(x) \, dx \] En ambos casos, por supuesto, suponemos que existen los valores esperados. En la sección anterior sobre propiedades básicas, probamos el cambio de teorema de variables cuando\( X \) tiene una distribución discreta y cuando\( X \) tiene una distribución continua pero\( r \) tiene rango contable. Ahora finalmente podemos terminar nuestra prueba en el caso continuo.
Supongamos que\(X\) tiene una distribución continua\(S\) con función de densidad de probabilidad\(f\), y\(r: S \to \R\). Entonces\[ \E\left[r(X)\right] = \int_S r(x) f(x) \, dx \]
Prueba
Supongamos primero que no\( r \) es negativo. Del teorema anterior,\[ \E\left[r(X)\right] = \int_0^\infty \P\left[r(X) \gt t\right] \, dt = \int_0^\infty \int_{r^{-1}(t, \infty)} f(x) \, dx \, dt = \int_S \int_0^{r(x)} f(x) \, dt \, dx = \int_S r(x) f(x) \, dx \] para general\( r \), nos descomponemos en partes positivas y negativas, y utilizamos el resultado recién establecido. \ begin {align}\ E\ izquierda [r (X)\ derecha] & =\ E\ izquierda [r^+ (X) - r^- (X)\ derecha] =\ E\ izquierda [r^+ (X)\ derecha] -\ E\ izquierda [r^- (X)\ derecha]\\ & =\ int_s r^+ (x) f (x)\, dx -\ int_s _s r^- (x) f (x)\, dx =\ int_s\ izquierda [r^+ (x) - r^- (x)\ derecha] f (x)\, dx =\ int_s r (x) f (x)\, dx\ end {align}
Desigualdad de Jensens
Nuestra siguiente secuencia de ejercicios establecerá una desigualdad importante conocida como la desigualdad de Jensen, llamada así por Johan Jensen. Primero necesitamos una definición.
Una función de valor real\(g\) definida en un intervalo\(S \subseteq \R\) se dice que es convexa (o cóncava hacia arriba) en\(S\) si para cada uno\(t \in S\), existen números\(a\) y\(b\) (que puede depender de\(t\)), de tal manera que
- \(a + b t = g(t)\)
- \(a + bx \le g(x)\)para todos\(x \in S\)
La gráfica de\(x \mapsto a + b x\) se llama una línea de soporte para\( g \) at\(t\).
Por lo tanto, una función convexa tiene al menos una línea de soporte en cada punto del dominio
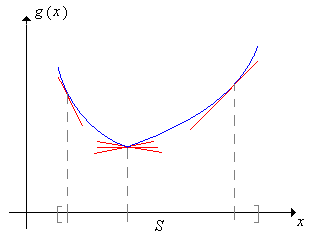
Puede estar más familiarizado con la convexidad en términos del siguiente teorema del cálculo: Si\(g\) tiene una segunda derivada continua, no negativa en\(S\), entonces\(g\) es convexa on\(S\) (ya que la línea tangente at\(t\) es una línea de soporte en\(t\) para cada uno\(t \in S\)). El siguiente resultado es la versión variable única de la desigualdad de Jensen
Si\(X\) toma valores en un intervalo\(S\) y\(g: S \to \R\) es convexo encendido\(S\), entonces\[ \E\left[g(X)\right] \ge g\left[\E(X)\right] \]
Prueba
Tenga en cuenta que\( \E(X) \in S \) así que vamos a\( y = a + b x \) ser una línea de apoyo para\( g \) al\( \E(X) \). Así\(a + b \E(X) = g[\E(X)]\) y\(a + b \, X \le g(X)\). Tomando valores esperados a través de la desigualdad da
\[ a + b \, \E(X) = g\left[\E(X)\right] \le \E\left[g(X)\right] \]La desigualdad de Jensens se extiende fácilmente a dimensiones superiores. La versión bidimensional es particularmente importante, ya que se utilizará para derivar varias desigualdades especiales en la sección sobre espacios vectoriales de variables aleatorias. Necesitamos dos definiciones.
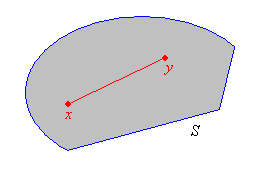
Un conjunto\(S \subseteq \R^n\) es convexo si por cada par de puntos en\(S\), el segmento de línea que conecta esos puntos también se encuentra en\(S\). Es decir, si\(\bs x, \, \bs y \in S\) y\(p \in [0, 1]\) entonces\(p \bs x + (1 - p) \bs y \in S\).
Supongamos que\(S \subseteq \R^n\) es convexo. Una función\(g: S \to \R\) on\(S\) es convexa (o cóncava hacia arriba) si para cada uno\(\bs t \in S\), existen\(a \in \R\) y\(\bs b \in \R^n\) (dependiendo de\(\bs t\)) tal que
- \(a + \bs b \cdot \bs t = g(\bs t)\)
- \(a + \bs b \cdot \bs x \le g(\bs x)\)para todos\(\bs x \in S\)
El gráfico de\(\bs x \mapsto a + \bs b \cdot \bs x\) se llama hiperplano de soporte para\( g \) at\(\bs t \).
En\( \R^2 \) un hiperplano de soporte se encuentra un plano ordinario. A partir del cálculo, si\(g\) tiene segundas derivadas continuas encendidas\(S\) y tiene una matriz de segunda derivada positiva no definida, entonces\(g\) es convexa encendida\(S\). Supongamos ahora que\(\bs X = (X_1, X_2, \ldots, X_n)\) toma valores adentro\(S \subseteq \R^n\), y deja\(\E(\bs X ) = (\E(X_1), \E(X_2), \ldots, \E(X_n))\). El siguiente resultado es la versión general de la inqulaidad de Jensen.
Si\(S\) es convexo y\(g: S \to \R\) es convexo\(S\) entonces
\[ \E\left[g(\bs X)\right] \ge g\left[\E(\bs X)\right] \]Prueba
Primero\( \E(\bs X) \in S \), así que vamos a\( y = a + \bs b \cdot \bs x \) ser un hiperplano de soporte para\( g \) at\( \E(\bs X) \). Así\(a + \bs b \cdot \E(\bs X) = g[\E(\bs X)]\) y\(a + \bs b \cdot \bs X \le g(\bs X)\). Tomando valores esperados a través de la desigualdad da\[ a + \bs b \cdot \E(\bs X ) = g\left[\E(\bs X)\right] \le \E\left[g(\bs X)\right] \]
Estudiaremos el valor esperado de vectores aleatorios y matrices con más detalle en una sección posterior. Tanto en el caso\(n\) unidimensional como en el caso, una función\(g: S \to \R\) es cóncava (o cóncava hacia abajo) si se invierte la desigualdad en la definición. La desigualdad de Jensen también revierte.
Valor esperado en términos de la función cuantil
Si\( X \) tiene una distribución continua con soporte en un intervalo de\( \R \), entonces hay una fórmula simple (pero no muy conocida) para el valor esperado de\( X \) como la integral de la función cuantil de\( X \). Aquí está el resultado general:
Supongamos que\( X \) tiene una distribución continua con soporte en un intervalo\( (a, b) \subseteq \R \). Dejar\( F \) denotar la función de distribución acumulativa de\( X \) por lo que\( F^{-1} \) es la función cuantil de\( X \). Si\( g: (a, b) \to \R \) entonces (suponiendo que existe el valor esperado),\[ \E[g(X)] = \int_0^1 g\left[F^{-1}(p)\right] dp, \quad n \in \N \]
Prueba
Supongamos que\( X \) tiene función de densidad de probabilidad\( f \), aunque el teorema es cierto sin esta suposición. Bajo el supuesto de que\( X \) tiene una distribución continua con soporte en el intervalo\( (a, b) \), la función de distribución\( F \) está aumentando estrictamente\( (a, b) \), y la función cuantil\( F^{-1} \) es la inversa ordinaria de\( F \). Sustituyendo\( p = F(x) \),\( dp = F^\prime(x) \, dx = f(x) \, dx \) tenemos\[ \int_0^1 g\left[F^{-1}(p)\right] d p = \int_a^b g\left(F^{-1}[F(x)]\right) f(x) \, dx = \int_a^b g(x) f(x) \, dx = \E[g(X)] \]
Entonces en particular,\( \E(X) = \int_0^1 F^{-1}(p) \, dp \).
Ejemplos y Aplicaciones
Let\( a \in (0, \infty) \) y let\( \P(X = a) = 1 \), así que esa\( X \) es una variable aleatoria constante. Demostrar que la desigualdad de Markov es de hecho igualdad en\( x = a \).
Solución
Por supuesto\( \E(X) = a \). De ahí\( \P(X \ge a) = 1 \) y\( \E(X) / a = 1 \).
La distribución exponencial
Recordemos que la distribución exponencial es una distribución continua con función de densidad de probabilidad\(f\) dada por\[ f(t) = r e^{-r t}, \quad t \in [0, \infty) \] donde\(r \in (0, \infty)\) está el parámetro de tasa. Esta distribución es ampliamente utilizada para modelar tiempos de falla y otros tiempos de llegada
; en particular, la distribución gobierna el tiempo entre llegadas en el modelo de Poisson. La distribución exponencial se estudia en detalle en el capítulo sobre el Proceso de Poisson.
Supongamos que\(X\) tiene distribución exponencial con parámetro de tasa\(r\).
- Encuentra\(\E(X) \) usando la fórmula de distribución correcta.
- Encuentra\( \E(X) \) usando la fórmula de la función cuantil.
- Calcular ambos lados de la desigualdad de Markov.
Responder
- \( \int_0^\infty e^{-r t} \, dt = \frac{1}{r} \)
- \( \int_0^1 -\frac{1}{r} \ln(1 - p) \, dp = \frac{1}{r} \)
- \(e^{-r t} \lt \frac{1}{r t}\)para\( t \gt 0 \)
Abrir el experimento gamma. Mantener el valor predeterminado del parámetro de detención (\( n = 1 \)), que da la distribución exponencial. Varíe el parámetro de tasa\( r \) y anote la forma de la función de densidad de probabilidad y la ubicación de la media. Para diversos valores del parámetro de tasa, ejecute el experimento 1000 veces y compare la media de la muestra con la media de distribución.
La distribución geométrica
Recordemos que los ensayos de Bernoulli son ensayos independientes cada uno con dos resultados, que en el lenguaje de la confiabilidad, se llaman éxito y fracaso. La probabilidad de éxito en cada ensayo es\( p \in [0, 1] \). Un capítulo separado sobre los ensayos de Bernoulli explora este proceso aleatorio con más detalle. Se llama así por Jacob Bernoulli. Si\( p \in (0, 1) \), el número\( N \) de prueba del primer éxito tiene la distribución geométrica\(\N_+\) con parámetro éxito\(p\). La función de densidad de probabilidad\(f\) de\( N \) viene dada por\[ f(n) = p (1 - p)^{n - 1}, \quad n \in \N_+ \]
Supongamos que\(N\) tiene la distribución geométrica on\( \N_+ \) con parámetro\( p \in (0, 1) \).
- Encuentre\(\E(N)\) usando la fórmula de función de distribución correcta.
- Calcular ambos lados de la desigualdad de Markov.
- Encontrar\(\E(N \mid N \text{ is even })\).
Responder
- \( \sum_{n=0}^\infty (1 - p)^n = \frac{1}{p} \)
- \((1 - p)^{n-1} \lt \frac{1}{n p}, \quad n \in \N_+\)
- \(\frac{2 (1 - p)^2}{p (2 - p)^2}\)
Abrir el experimento binomial negativo. Mantener el valor predeterminado del parámetro de detención (\( k = 1 \)), que da la distribución geométrica. Varíe el parámetro de éxito\( p \) y anote la forma de la función de densidad de probabilidad y la ubicación de la media. Para diversos valores del parámetro de éxito, ejecute el experimento 1000 veces y compare la media de la muestra con la media de distribución.
La distribución de Pareto
Recordemos que la distribución de Pareto es una distribución continua con función de densidad de probabilidad\(f\) dada por\[ f(x) = \frac{a}{x^{a + 1}}, \quad x \in [1, \infty) \] donde\(a \in (0, \infty)\) es un parámetro. La distribución de Pareto lleva el nombre de Vilfredo Pareto. Se trata de una distribución de cola pesada que es ampliamente utilizada para modelar ciertas variables financieras. La distribución de Pareto se estudia en detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(X\) tiene la distribución de Pareto con parámetro\( a \gt 1 \).
- Encuentre\(\E(X)\) usando la fórmula de función de distribución correcta.
- Encuentra\( \E(X) \) usando la fórmula de la función cuantil.
- Encontrar\(\E(1 / X)\).
- Mostrar que\(x \mapsto 1 / x\) es convexo en\((0, \infty)\).
- Verificar la desigualdad de Jensen comparando\( \E(1 / X) \) y\( 1 \big/ \E(X) \).
Responder
- \(\int_0^1 1 \, dx + \int_1^\infty x^{-a} \, dx = \frac{a}{a - 1}\)
- \( \int_0^1 (1 - p)^{-1/a} dp = \frac{a}{a - 1} \)
- \(\frac{a}{a + 1}\)
- La convexidad de\( 1 / x \) es clara a partir de la gráfica. Tenga en cuenta también que\( \frac{d^2}{dx^2} \frac{1}{x} = \frac{2}{x^3} \gt 0 \) para\( x \gt 0 \).
- \(\frac{a}{a + 1} \gt \frac{a -1}{a}\)
Abra el simulador de distribución especial y seleccione la distribución de Pareto. Mantener el valor predeterminado del parámetro scale. Varíe el parámetro shape y anote la forma de la función de densidad de probabilidad y la ubicación de la media. Para diversos valores del parámetro shape, ejecute el experimento 1000 veces y compare la media de la muestra con la media de distribución.
Una distribución bivariada
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 2 (x + y)\) for\(0 \le x \le y \le 1\).
- Mostrar que el dominio de\(f\) es un conjunto convexo.
- Mostrar que\((x, y) \mapsto x^2 + y^2\) es convexo en el dominio de\(f\).
- Computar\(\E\left(X^2 + Y^2\right)\).
- Computar\(\left[\E(X)\right]^2 + \left[\E(Y)\right]^2\).
- Verificar la desigualdad de Jensen comparando (b) y (c).
Responder
- Tenga en cuenta que el dominio es una región triangular.
- La segunda matriz derivada es\( \left[\begin{matrix} 2 & 0 \\ 0 & 2\end{matrix}\right] \).
- \(\frac{5}{6}\)
- \(\frac{53}{72}\)
- \(\frac{5}{6} \gt \frac{53}{72}\)
Las medias aritméticas y geométricas
Supongamos que\(\{x_1, x_2, \ldots, x_n\}\) es un conjunto de números positivos. La media aritmética es al menos tan grande como la media geométrica:\[ \left(\prod_{i=1}^n x_i \right)^{1/n} \le \frac{1}{n}\sum_{i=1}^n x_i \]
Prueba
Dejar que\(X\) se distribuya uniformemente en\(\{x_1, x_2, \ldots, x_n\}\). Aplicamos la desigualdad de Jensen con la función de logaritmo natural, que es cóncava en\((0, \infty)\):\[ \E\left(\ln X \right) = \frac{1}{n} \sum_{i=1}^n \ln x_i = \ln \left[ \left(\prod_{i=1}^n x_i \right)^{1/n} \right] \le \ln\left[\E(X)\right] = \ln \left(\frac{1}{n}\sum_{i=1}^n x_i \right) \] Tomar exponenciales de cada lado da la desigualdad.


