4.6: Generando funciones
- Page ID
- 151946
Como es habitual, nuestro punto de partida es un experimento aleatorio modelado por un sace de probabilidad\((\Omega, \mathscr F, \P)\). Una función generadora de una variable aleatoria de valor real es un valor esperado de una cierta transformación de la variable aleatoria que involucra otra variable (determinista). La mayoría de las funciones generadoras comparten cuatro propiedades importantes:
- En condiciones suaves, la función generadora determina completamente la distribución de la variable aleatoria.
- La función generadora de una suma de variables independientes es el producto de las funciones generadoras
- Los momentos de la variable aleatoria se pueden obtener a partir de las derivadas de la función generadora.
- La convergencia ordinaria (puntual) de una secuencia de funciones generadoras corresponde a la convergencia especial de las distribuciones correspondientes.
La propiedad 1 es quizás la más importante. A menudo se muestra que una variable aleatoria tiene una cierta distribución al mostrar que la función generadora tiene cierta forma. El proceso de recuperación de la distribución de la función generadora se conoce como inversión. La propiedad 2 se utiliza frecuentemente para determinar la distribución de una suma de variables independientes. Por el contrario, recordemos que la función de densidad de probabilidad de una suma de variables independientes es la convolución de las funciones de densidad individuales, una operación mucho más complicada. La propiedad 3 es útil porque a menudo calcular momentos desde la función generadora es más fácil que calcular los momentos directamente desde la función de densidad de probabilidad. La última propiedad se conoce como el teorema de la continuidad. A menudo es más fácil mostrar la convergencia de las funciones generadoras que demostrar la convergencia de las distribuciones directamente.
El valor numérico de la función generadora a un valor particular de la variable libre no es de interés, por lo que generar funciones puede parecer poco intuitivo al principio. Pero el punto importante es que la función generadora en su conjunto codifica toda la información en la distribución de probabilidad de una manera muy útil. Las funciones generadoras son herramientas importantes y valiosas en la probabilidad, como lo son en otras áreas de las matemáticas, desde la combinatoria hasta las ecuaciones diferenciales.
Estudiaremos las tres funciones generadoras de la siguiente lista, que corresponden a niveles crecientes de generalidad. El puño es el más restrictivo, pero también de lejos el más simple, ya que la teoría reduce a hechos básicos sobre series de poder que recordarás del cálculo. El tercero es el más general y aquel para el que la teoría es más completa y elegante, pero también requiere conocimientos básicos de análisis complejos. El del medio es quizás el más utilizado, y es suficiente para la mayoría de las distribuciones en probabilidad aplicada.
- la función de generación de probabilidad
- la función de generación de momento
- la función característica
También estudiaremos la función característica de las distribuciones multivariadas, aunque se mantienen resultados análogos para los otros dos tipos. En la teoría básica a continuación, asegúrate de probar las pruebas tú mismo antes de leer las que aparecen en el texto.
Teoría Básica
La función de generación de probabilidad
Para nuestra primera función generadora, supongamos que\(N\) es una variable aleatoria que toma valores\(\N\).
La función\(P\) de generación de probabilidad de\(N\) se define por\[ P(t) = \E\left(t^N\right) \] para todos\(t \in \R\) para los cuales existe el valor esperado en\( \R \).
Es decir,\( P(t) \) se define cuándo\( \E\left(|t|^N\right) \lt \infty \). La función de generación de probabilidad se puede escribir muy bien en términos de la función de densidad de probabilidad.
Supongamos que\(N\) tiene función de densidad de probabilidad\(f\) y función generadora de probabilidad\(P\). Entonces\[ P(t) = \sum_{n=0}^\infty f(n) t^n, \quad t \in (-r, r) \] donde\( r \in [1, \infty] \) esta el radio de convergencia de la serie.
Prueba
La expansión se desprende del teorema del cambio discreto de variables para el valor esperado. Tenga en cuenta que la serie es una serie de potencia en\( t \), y por lo tanto por cálculo básico, converge absolutamente para\( t \in (-r, r) \) donde\( r \in [0, \infty] \) está el radio de convergencia. Pero ya que\( \sum_{n=0}^\infty f(n) = 1 \) debemos tener\( r \ge 1 \), y la serie converge absolutamente al menos para\( t \in [-1, 1] \).
En el lenguaje de la combinatoria,\(P\) es la función generadora ordinaria de\(f\). Por supuesto, si\( N \) solo toma un conjunto finito de valores en\( \N \) entonces\( r = \infty \). Recordemos del cálculo que una serie de potencias puede diferenciarse término por término, al igual que un polinomio. Cada serie derivada tiene el mismo radio de convergencia que la serie original (pero puede comportarse de manera diferente en los puntos finales del intervalo de convergencia). Denotamos la derivada del orden\(n\) por\(P^{(n)}\). Recordemos también que si\(n \in \N\) y\(k \in \N\) con\(k \le n\), entonces el número de permutaciones de tamaño\(k\) elegido de una población de\(n\) objetos es\[ n^{(k)} = n (n - 1) \cdots (n - k + 1) \] El siguiente teorema es el resultado de inversión para funciones generadoras de probabilidad: la función generadora completamente determina la distribución.
Supongamos nuevamente que\(N\) tiene función de densidad de probabilidad\(f\) y función generadora de probabilidad\(P\). Entonces\[ f(k) = \frac{P^{(k)}(0)}{k!}, \quad k \in \N \]
Prueba
Este es un resultado estándar de la teoría de la serie de poder. Diferenciar\( k \) tiempos da\( P^{(k)}(t) = \sum_{n=k}^\infty n^{(k)} f(n) t^{n-k} \) para\( t \in (-r, r) \). De ahí\( P^{(k)}(0) = k^{(k)} f(k) = k! f(k) \)
Nuestro siguiente resultado no es particularmente importante, pero tiene cierta curiosidad.
\(\P(N \text{ is even}) = \frac{1}{2}\left[1 + P(-1)\right]\).
Prueba
Tenga en cuenta que\[ P(1) + P(-1) = \sum_{n=0}^\infty f(n) + \sum_{n=0}^\infty (-1)^n f(n) = 2 \sum_{k=0}^\infty f(2 k) = 2 \P(N \text{ is even }) \] Podemos combinar las dos suma ya que sabemos que las series convergen absolutamente en 1 y\(-1\).
Recordemos que el momento factorial\( N \) de orden\( k \in \N \) es\( \E\left[N^{(k)}\right] \). Los momentos factoriales se pueden calcular a partir de las derivadas de la función generadora de probabilidad. Los momentos factoriales, a su vez, determinan los momentos ordinarios alrededor de 0 (a veces denominados momentos crudos).
Supongamos que el radio de convergencia\(r \gt 1\). Entonces\(P^{(k)}(1) = \E\left[N^{(k)}\right]\) para\(k \in \N\). En particular,\(N\) tiene momentos finitos de todos los pedidos.
Prueba
Como antes,\( P^{(k)}(t) = \sum_{n=k}^\infty n^{(k)} f(n) t^{n-k} \) para\( t \in (-r, r) \). De ahí que si\( r \gt 1 \) entonces\( P^{(k)}(1) = \sum_{n=k}^\infty n^{(k)} f(n) = \E\left[N^{(k)}\right] \)
Supongamos otra vez eso\( r \gt 1 \). Entonces
- \(\E(N) = P^\prime(1)\)
- \(\var(N) = P^{\prime \prime}(1) + P^\prime(1)\left[1 - P^\prime(1)\right]\)
Prueba
- \( \E(N) = \E\left[N^{(1)}\right] = P^\prime(1) \).
- \( \E\left(N^2\right) = \E[N (N - 1)] + \E(N) = \E\left[N^{(2)}\right] + \E(N) = P^{\prime\prime}(1) + P^\prime(1) \). De ahí a partir de (a),\( \var(N) = P^{\prime\prime}(1) + P^\prime(1) - \left[P^\prime(1)\right]^2 \).
Supongamos que\(N_1\) y\(N_2\) son variables aleatorias independientes que toman valores\(\N\), con funciones generadoras de probabilidad\(P_1\) y\(P_2\) que tienen radios de convergencia\( r_1 \) y\( r_2 \), respectivamente. Entonces la función generadora de probabilidad\( P \) de\(N_1 + N_2\) viene dada por\(P(t) = P_1(t) P_2(t)\) for\( \left|t\right| \lt r_1 \wedge r_2 \).
Prueba
Recordemos que el producto esperado de las variables independientes es el producto de los valores esperados. De ahí\[ P(t) = \E\left(t^{N_1 + N_2}\right) = \E\left(t^{N_1} t^{N_2}\right) = \E\left(t^{N_1}\right) \E\left(t^{N_2}\right) = P_1(t) P_2(t), \quad \left|t\right| \lt r_1 \wedge r_2 \]
La función de generación de momento
Nuestra siguiente función generadora se define de manera más general, por lo que en esta discusión asumimos que las variables aleatorias son de valor real.
La función generadora de momento de\(X\) es la función\(M\) definida por\[ M(t) = \E\left(e^{tX}\right), \quad t \in \R \]
Obsérvese que ya que\(e^{t X} \ge 0\) con probabilidad 1,\(M(t)\) existe, como número real o\(\infty\), para cualquiera\(t \in \R\). Pero como veremos, nuestro interés estará en el dominio donde\( M(t) \lt \infty \).
Supongamos que\(X\) tiene una distribución continua\(\R\) con función de densidad de probabilidad\(f\). Entonces\[ M(t) = \int_{-\infty}^\infty e^{t x} f(x) \, dx \]
Prueba
Esto se desprende del cambio de teorema de variables por valor esperado.
Así, la función generadora de momento de\(X\) está estrechamente relacionada con la transformada de Laplace de la función de densidad de probabilidad\(f\). La transformación de Laplace lleva el nombre de Pierre Simon Laplace, y es ampliamente utilizada en muchas áreas de las matemáticas aplicadas, particularmente ecuaciones diferenciales. El teorema básico de inversión para funciones generadoras de momento (similar al teorema de inversión para las transformaciones de Laplace) establece que si\(M(t) \lt \infty\) para\(t\) en un intervalo abierto alrededor de 0, entonces determina\(M\) completamente la distribución de\(X\). Así, si dos distribuciones on\(\R\) tienen funciones de generación de momento que son iguales (y finitas) en un intervalo abierto alrededor de 0, entonces las distribuciones son las mismas.
Supongamos que\(X\) tiene la función de generación de momento\(M\) que es finita en un intervalo abierto\( I \) alrededor de 0. Entonces\(X\) tiene momentos de todos los pedidos y\[ M(t) = \sum_{n=0}^\infty \frac{\E\left(X^n\right)}{n!} t^n, \quad t \in I \]
Prueba
Bajo las hipótesis, el operador de valor esperado puede intercambiarse con la serie infinita para la función exponencial:\[ M(t) = \E\left(e^{t X}\right) = \E\left(\sum_{n=0}^\infty \frac{X^n}{n!} t^n\right) = \sum_{n=0}^\infty \frac{\E(X^n)}{n!} t^n, \quad t \in I \] El intercambio es un caso especial del teorema de Fubini, llamado así por Guido Fubini. Para más detalles consulte la sección avanzada sobre propiedades de la integral en el capítulo sobre Distribuciones.
Entonces bajo la suposición finita en el último teorema, la función generadora de momento, como la función generadora de probabilidad, es una serie de potencia en\( t \).
Supongamos nuevamente que\( X \) tiene momento generando función\( M \) que es finita en un intervalo abierto alrededor de 0. Entonces\(M^{(n)}(0) = \E\left(X^n\right)\) para\(n \in \N\)
Prueba
A esto le sigue el mismo argumento anterior para la PGF:\( M^{(n)}(0) / n! \) es el coeficiente de orden\( n \) en la serie de potencias anterior, a saber\( \E\left(X^n\right) / n! \). De ahí\( M^{(n)}(0) = \E\left(X^n\right) \).
Así, las derivadas de la función generadora de momento a 0 determinan los momentos de la variable (de ahí el nombre). En el lenguaje de la combinatoria, la función generadora de momentos es la función generadora exponencial de la secuencia de momentos. Así, una variable aleatoria que no tiene momentos finitos de todos los órdenes no puede tener una función generadora de momentos finitos. Incluso cuando una variable aleatoria tiene momentos de todos los órdenes, la función de generación de momento puede no existir. A continuación se construye un contraejemplo.
Para las variables aleatorias no negativas (que son muy comunes en las aplicaciones), el dominio donde la función generadora de momentos es finita es fácil de entender.
Supongamos que\( X \) toma valores\( [0, \infty) \) y tiene función de generación de momento\( M \). Si\( M(t) \lt \infty \) para\( t \in \R \) entonces\( M(s) \lt \infty \) para\( s \le t \).
Prueba
Ya que\( X \ge 0 \), si\( s \le t \) entonces\( s X \le t X \) y por lo tanto\( e^{s X} \le e^{t X} \). De ahí\( \E\left(e^{s X}\right) \le \E\left(e^{t X} \right) \).
Entonces para una variable aleatoria no negativa, ya sea\( M(t) \lt \infty \) para todos\( t \in \R \) o existe\( r \in (0, \infty) \) tal que\( M(t) \lt \infty \) para\( t \lt r \). Por supuesto, hay resultados complementarios para las variables aleatorias no positivas, pero tales variables son mucho menos comunes. A continuación consideramos lo que sucede con la función generadora de momento bajo algunas transformaciones simples de las variables aleatorias.
Supongamos que\(X\) tiene función generadora de momento\(M\) y eso\(a, \, b \in \R\). El momento que genera la función\( N \) de\(Y = a + b X\) está dada por\(N(t) = e^{a t} M(b t)\) for\( t \in \R \).
Prueba
\( \E\left[e^{t (a + b X)}\right] = \E\left(e^{t a} e^{t b X}\right) = e^{t a} \E\left[e^{(t b) X}\right] = e^{a t} M(b t) \)para\ (t\ in\ R).
Recordemos que si\( a \in \R \) y\( b \in (0, \infty) \) entonces la transformación\( a + b X \) es una transformación a escala de ubicación en la distribución de\( X \), con parámetro de ubicación\(a\) y parámetro de escala\(b\). Las transformaciones a escala de ubicación surgen con frecuencia cuando se cambian las unidades, como la longitud de pulgadas a centímetros o la temperatura de grados Fahrenheit a grados Celsius.
Supongamos que\(X_1\) y\(X_2\) son variables aleatorias independientes con funciones generadoras de momento\(M_1\) y\(M_2\) respectivamente. El momento que genera la función\( M \) de\(Y = X_1 + X_2\) está dada por\(M(t) = M_1(t) M_2(t)\) for\( t \in \R \).
Prueba
Al igual que con la PGF, la prueba para el MGF se basa en la ley de exponentes y en el hecho de que el valor esperado de un producto de variables independientes es producto de los valores esperados:\[ \E\left[e^{t (X_1 + X_2)}\right] = \E\left(e^{t X_1} e^{t X_2}\right) = \E\left(e^{t X_1}\right) \E\left(e^{t X_2}\right) = M_1(t) M_2(t), \quad t \in \R \]
La función de generación de probabilidad de una variable se puede convertir fácilmente en la función de generación de momento de la variable.
Supongamos que\(X\) es una variable aleatoria que toma valores\(\N\) con función de generación de probabilidad\(G\) que tiene radio de convergencia\( r \). El momento que genera la función\( M \) de\(X\) está dada por\(M(t) = G\left(e^t\right)\) for\( t \lt \ln(r) \).
Prueba
\( M(t) = \E\left(e^{t X}\right) = \E\left[\left(e^t\right)^X\right] = G\left(e^t\right) \)para\( e^t \lt r \).
El siguiente teorema da los límites de Chernoff, llamado así por el matemático Herman Chernoff. Estos son límites superiores en los eventos de cola de una variable aleatoria.
Si\(X\) tiene función de generación de momento\(M\) entonces
- \(\P(X \ge x) \le e^{-t x} M(t)\)para\(t \gt 0\)
- \(\P(X \le x) \le e^{-t x} M(t)\)para\(t \lt 0\)
Prueba
- De la desigualdad de Markov,\(\P(X \ge x) = \P\left(e^{t X} \ge e^{t x}\right) \le \E\left(e^{t X}\right) \big/ e^{t x} = e^{-t x} M(t) \) si\(t \gt 0\).
- Del mismo modo,\(\P(X \le x) = \P\left(e^{t X} \ge e^{t x}\right) \le e^{-t x} M(t) \) si\(t \lt 0\).
Naturalmente, el mejor ligado de Chernoff (ya sea en (a) o (b)) se obtiene encontrando\(t\) que minimiza\(e^{-t x} M(t)\).
La función característica
Nuestra última función generadora es la más agradable desde el punto de vista matemático. Una vez más, asumimos que nuestras variables aleatorias son de valor real.
La función característica de\(X\) es la función\( \chi \) definida por\[ \chi(t) = \E\left(e^{i t X}\right) = \E\left[\cos(t X)\right] + i \E\left[\sin(t X)\right], \quad t \in \R \]
Obsérvese que\(\chi\) es una función compleja valorada, por lo que esta subsección requiere algunos conocimientos básicos de análisis complejos. La función\(\chi\) se define para todos\(t \in \R\) porque la variable aleatoria en el valor esperado está limitada en magnitud. Efectivamente,\(\left|e^{i t X}\right| = 1\) para todos\(t \in \R\). Muchas de las propiedades de la función característica son más elegantes que las propiedades correspondientes de las funciones generadoras de probabilidad o momento, porque la función característica siempre existe.
Si\(X\) tiene una distribución continua\(\R\) con función de densidad de probabilidad\(f\) y función característica\( \chi \) entonces\[ \chi(t) = \int_{-\infty}^{\infty} e^{i t x} f(x) dx, \quad t \in \R \]
Prueba
Esto se desprende del cambio de teorema de variables por valor esperado, aunque una versión compleja.
Así, la función característica de\(X\) está estrechamente relacionada con la transformada de Fourier de la función de densidad de probabilidad\(f\). La transformada de Fourier lleva el nombre de Joseph Fourier, y es ampliamente utilizada en muchas áreas de las matemáticas aplicadas.
Al igual que con otras funciones generadoras, la función característica determina completamente la distribución. Es decir, variables aleatorias\(X\) y\(Y\) tienen la misma distribución si y sólo si tienen la misma función característica. En efecto, la fórmula general de inversión dada a continuación es una fórmula para computar ciertas combinaciones de probabilidades a partir de la función característica.
Supongamos nuevamente que\( X \) tiene función característica\( \chi \). Si\( a, \, b \in \R \) y\(a \lt b\) entonces\[ \int_{-n}^n \frac{e^{-i a t} - e^{- i b t}}{2 \pi i t} \chi(t) \, dt \to \P(a \lt X \lt b) + \frac{1}{2}\left[\P(X = b) - \P(X = a)\right] \text{ as } n \to \infty \]
Las combinaciones de probabilidad en el lado derecho determinan completamente la distribución de\(X\). Una fórmula de inversión especial se mantiene para distribuciones continuas:
Supongamos que\(X\) tiene una distribución continua con función de densidad de probabilidad\(f\) y función característica\( \chi \). En cada punto\(x \in \R\) donde\(f\) es diferenciable,\[ f(x) = \frac{1}{2 \pi} \int_{-\infty}^\infty e^{-i t x} \chi(t) \, dt \]
Esta fórmula es esencialmente la transformada inversa de Fourrier. Al igual que con las otras funciones generadoras, la función característica se puede utilizar para encontrar los momentos de\(X\). Además, esto se puede hacer incluso cuando solo existen algunos de los momentos.
Supongamos nuevamente que\( X \) tiene función característica\( \chi \). Si\(n \in \N_+\) y\(\E\left(\left|X^n\right|\right) \lt \infty\). Entonces\[ \chi(t) = \sum_{k=0}^n \frac{\E\left(X^k\right)}{k!} (i t)^k + o(t^n) \] y por lo tanto\(\chi^{(n)}(0) = i^n \E\left(X^n\right)\).
Detalles
Recordemos que el último término es una función genérica que satisface\(o(t^n) / t^n \to 0\) como\(t \to \infty\).
A continuación consideramos cómo se cambia la función característica bajo algunas transformaciones simples de las variables.
Supongamos que\(X\) tiene función característica\(\chi\) y eso\(a, \, b \in \R\). La función característica\( \psi \) de\(Y = a + b X\) está dada por\(\psi(t) = e^{i a t} \chi(b t)\) for\( t \in \R \).
Prueba
La prueba es igual que la del MGF:\( \psi(t) = \E\left[e^{i t (a + b X)}\right] = \E\left(e^{i t a} e^{i t b X}\right) = e^{i t a} \E\left[e^{i (t b) X}\right] = e^{i a t} \chi(b t) \) para\(t \in \R\).
Supongamos que\(X_1\) y\(X_2\) son variables aleatorias independientes con funciones características\(\chi_1\) y\(\chi_2\) respectivamente. La función característica\( \chi \) de\(Y = X_1 + X_2\) está dada por\(\chi(t) = \chi_1(t) \chi_2(t)\) for\( t \in \R \).
Prueba
Nuevamente, la prueba es igual que la del MGF:\[ \chi(t) = \E\left[e^{i t (X_1 + X_2)}\right] = \E\left(e^{i t X_1} e^{i t X_2}\right) = \E\left(e^{i t X_1}\right) \E\left(e^{i t X_2}\right) = \chi_1(t) \chi_2(t), \quad t \in \R \]
La función característica de una variable aleatoria se puede obtener a partir de la función generadora de momento, bajo la condición básica de existencia que vimos antes.
Supongamos que\(X\) tiene la función de generación de momento\(M\) que satisface\(M(t) \lt \infty\)\(t\) en un intervalo abierto\(I\) alrededor de 0. Entonces la función característica\(\chi\) de\(X\) satisface\(\chi(t) = M(i t)\) para\(t \in I\).
La propiedad final importante de las funciones características que discutiremos se relaciona con la convergencia en la distribución. Supongamos que\((X_1, X_2, \ldots)\) es una secuencia de valores reales aleatorios con funciones características\((\chi_1, \chi_2, \ldots)\) respectivamente. Dado que solo nos preocupan las distribuciones, las variables aleatorias no necesitan definirse en el mismo espacio de probabilidad.
El teorema de la continuidad
- Si la distribución de\(X_n\) converge a la distribución de una variable aleatoria\(X\) como\(n \to \infty\) y\(X\) tiene función característica\(\chi\), entonces\(\chi_n(t) \to \chi(t)\) como\(n \to \infty\) para todos\(t \in \R\).
- Por el contrario, si\(\chi_n(t)\) converge a una función\(\chi(t)\) como\(n \to \infty\) para\(t\) en un intervalo abierto alrededor de 0, y si\(\chi\) es continuo en 0, entonces\(\chi\) es la función característica de una variable aleatoria\(X\), y la distribución de\(X_n\) converge a la distribución de \(X\)como\(n \to \infty\).
Existen versiones análogas del teorema de continuidad para funciones generadoras de probabilidad y funciones generadoras de momento. El teorema de continuidad puede ser utilizado para probar el teorema del límite central, uno de los teoremas fundamentales de la probabilidad. Además, el teorema de continuidad tiene una generalización directa a las distribuciones en\(\R^n\).
La función característica conjunta
Todas las funciones generadoras que hemos discutido tienen extensiones multivariadas. Sin embargo, discutiremos la extensión solo para la función característica, la más importante y versátil de las funciones generadoras. Hay resultados análogos para las otras funciones generadoras. Entonces en esta discusión, asumimos que\((X, Y)\) es un vector aleatorio para nuestro experimento, tomando valores en\(\R^2\).
La función característica (conjunta)\( \chi \) de\((X, Y)\) se define por\[ \chi(s, t) = \E\left[\exp(i s X + i t Y)\right], \quad (s, t) \in \R^2 \]
Una vez más, el hecho más importante es que determina\(\chi\) completamente la distribución: dos vectores aleatorios que toman valores en\(\R^2\) tienen la misma función característica si y sólo si tienen la misma distribución.
Los momentos conjuntos se pueden obtener a partir de las derivadas de la función característica.
Supongamos que\( (X, Y) \) tiene función característica\( \chi \). Si\(m, \, n \in \N\) y\(\E\left(\left|X^m Y^n\right|\right) \lt \infty\) entonces\[ \chi^{(m, n)}(0, 0) = e^{i \, (m + n)} \E\left(X^m Y^n\right) \]
Las funciones características marginales y la función característica de la suma se pueden obtener fácilmente de la función característica conjunta:
Supongamos de nuevo que\( (X, Y) \) tiene función característica\( \chi \)\(\chi_1\), y let\(\chi_2\),, y\(\chi_+\) denotar las funciones características de\(X\)\(Y\), y\(X + Y\), respectivamente. Para\(t \in \R\)
- \(\chi(t, 0) = \chi_1(t)\)
- \(\chi(0, t) = \chi_2(t)\)
- \(\chi(t, t) = \chi_+(t)\)
Prueba
Los tres resultados siguen inmediatamente de las definiciones.
Supongamos de nuevo que\( \chi_1 \)\( \chi_2 \),, y\( \chi \) son las funciones características de\(X\)\(Y\), y\( (X, Y) \) respectivamente. Entonces\( X \) y\( Y \) son independientes si y sólo si\(\chi(s, t) = \chi_1(s) \chi_2(t)\) por todos\((s, t) \in \R^2\).
Naturalmente, los resultados para funciones características bivariadas tienen analogías en el caso multivariado general. Sólo la notación es más complicada.
Ejemplos y Aplicaciones
Como siempre, asegúrate de probar los problemas computacionales tú mismo antes de ampliar las soluciones y respuestas en el texto.
Dados
Recordemos que un dado plano as-seis es un dado de seis lados para el cual las caras numeradas 1 y 6 tienen probabilidad\( \frac{1}{4} \) cada una, mientras que las caras numeradas 2, 3, 4 y 5 tienen probabilidad\( \frac{1}{8} \) cada una. De manera similar, un dado plano de 3-4 es un dado de seis lados para el cual las caras numeradas 3 y 4 tienen probabilidad\( \frac{1}{4} \) cada una, mientras que las caras numeradas 1, 2, 5 y 6 tienen probabilidad\( \frac{1}{8} \) cada una.
Supongamos que se enrollan una matriz plana ace-seis y una matriz plana 3-4. Utilice funciones de generación de probabilidad para encontrar la función de densidad de probabilidad de la suma de las puntuaciones.
Solución
Dejar\( X \) y\( Y \) denotar la puntuación en el dado as-seis y el troquel plano 3-4, respectivamente. Entonces\( X \) y\( Y \) tener PGF\( P \) y\( Q \) dado por\ begin {align*} P (t) &=\ frac {1} {4} t +\ frac {1} {8} t^2 +\ frac {1} {8} t^3 +\ frac {1} {8} t^4 +\ frac {1} {8} t^5 +\ frac {1} {4} t^6,\ quad t\ in\ R\\ Q (t) &=\ frac {1} {8} t +\ frac {1} {8} t^2 +\ frac {1} {4} t^3 +\ frac {1} {4} t^4 +\ frac {1} {8} t^5 +\ frac {1} {8} t^6,\ quad t\ in\ R\ end {align*} De ahí\( X + Y \) tiene PGF\( P Q \). Expandiendo (un programa de álgebra de computadora ayuda) da\[ P(t) Q(t) = \frac{1}{32} t^2 + \frac{3}{64} t^3 + \frac{3}{32} t^4 + \frac{1}{8} t^5 + \frac{1}{8} t^6 + \frac{5}{32} t^7 + \frac{1}{8} t^8 + \frac{1}{8} t^9 + \frac{3}{32} t^{10} + \frac{3}{64} t^{11} + \frac{1}{32} t^{12}, \quad t \in \R\] Así el PDF\( f \) de\( X + Y \) está dado por\( f(2) = f(12) = \frac{1}{32} \)\( f(3) = f(11) = \frac{3}{64} \),,\( f(4) = f(10) = \frac{3}{32} \),\( f(5) = f(6) = f(8) = f(9) = \frac{1}{8} \) y\( f(7) = \frac{5}{32} \).
Se rotan dos dados justos de 6 lados. Una tiene caras numeradas\( (0, 1, 2, 3, 4, 5) \) y la otra caras numeradas\( (0, 6, 12, 18, 24, 30) \). Utilice funciones de generación de probabilidad para encontrar la función de densidad de probabilidad de la suma de las puntuaciones e identificar la distribución.
Solución
Dejar\( X \) y\( Y \) denotar la puntuación en el primer dado y el segundo dado descrito, respectivamente. Entonces\( X \) y\( Y \) tener PGF\( P \) y\( Q \) dado por\ begin {align*} P (t) &=\ frac {1} {6}\ sum_ {k=0} ^5 t^k\ quad t\ in\ R\ Q (t) &=\ frac {1} {6}\ sum_ {j=0} ^5 t^ {6 j}\ quad t\ in\ R\ end {align*} De ahí\( X + Y \) tiene PGF\( P Q \). Simplificando da\[ P(t) Q(t) = \frac{1}{36} \sum_{j=0}^5 \sum_{k=0}^5 t^{6 j + k} = \frac{1}{36} \sum_{n=0}^{35} t^n, \quad t \in \R\] Por lo tanto,\( X + Y \) se distribuye uniformemente en\( \{0, 1, 2, \ldots, 35\} \).
Supongamos que la variable aleatoria\( Y \) tiene función de generación de probabilidad\( P \) dada por\[ P(t) = \left(\frac{2}{5} t + \frac{3}{10} t^2 + \frac{1}{5} t^3 + \frac{1}{10} t^4\right)^5, \quad t \in \R \]
- Interpretar\( Y \) en términos de rodar dados.
- Utilice la función de generación de probabilidad para encontrar los dos primeros momentos factoriales de\( Y \).
- Use (b) para encontrar la varianza de\( Y \).
Contestar
- Un dado de cuatro lados tiene caras numeradas\((1, 2, 3, 4)\) con probabilidades respectivas\( \left(\frac{2}{5}, \frac{3}{10}, \frac{1}{5}, \frac{1}{10}\right) \). \( Y \)es la suma de las puntuaciones cuando el dado se enrolla 5 veces.
- \( \E(Y) = P^\prime(1) = 10 \),\( \E[Y(Y - 1)] = P^{\prime \prime}(1) = 95 \)
- \( \var(Y) = 5 \)
Juicios de Bernoulli
Supongamos que\(X\) es un indicador variable aleatoria con\(p = \P(X = 1)\), donde\(p \in [0, 1]\) es un parámetro. Entonces\(X\) tiene función de generación de probabilidad\(P(t) = 1 - p + p t\) para\(t \in \R\).
Prueba
\( P(t) = \E\left(t^X\right) = t^0 (1 - p) + t^1 p = 1 - p + p t \)para\( t \in \R \).
Recordemos que un proceso de ensayos de Bernoulli es una secuencia\((X_1, X_2, \ldots)\) de variables aleatorias indicadoras independientes, distribuidas idénticamente. En el lenguaje habitual de confiabilidad,\(X_i\) denota el resultado del ensayo\(i\), donde 1 denota éxito y 0 denota fracaso. La probabilidad de éxito\(p = \P(X_i = 1)\) es el parámetro básico del proceso. El proceso lleva el nombre de Jacob Bernoulli. Un capítulo separado sobre los Juicios de Bernoulli explora este proceso con más detalle.
Porque\(n \in \N_+\), el número de éxitos en los primeros\(n\) ensayos es\(Y_n = \sum_{i=1}^n X_i\). Recordemos que esta variable aleatoria tiene la distribución binomial con parámetros\(n\) y\(p\), que tiene la función de densidad de probabilidad\( f_n \) dada por\[ f_n(y) = \binom{n}{y} p^y (1 - p)^{n - y}, \quad y \in \{0, 1, \ldots, n\} \]
\(Y_n\)La variable aleatoria tiene una función de generación de probabilidad\(P_n\) dada por\(P_n(t) = (1 - p + p t)^n\) for\( t \in \R \).
Prueba
Esto se desprende inmediatamente del PGF de una variable indicadora y el resultado para sumas de variables independientes.
La variable Rando\(Y_n\) tiene los siguientes parámetros:
- \(\E\left[Y_n^{(k)}\right] = n^{(k)} p^k\)
- \(\E\left(Y_n\right) = n p\)
- \(\var\left(Y_n\right) = n p (1 - p)\)
- \(\P(Y_n \text{ is even}) = \frac{1}{2}\left[1 - (1 - 2 p)^n\right]\)
Prueba
- Diferenciación repetida da\( P^{(k)}(t) = n^{(k)} p^k (1 - p + p t)^{n-k} \). De ahí\( P^{(k)}(1) = n^{(k)} p^k \), que es\( \E\left[X^{(k)} \right]\) por el momento resultado anterior.
- Esto se desprende de la fórmula para la media.
- Esto se desprende de la fórmula de varianza.
- Esto se desprende de la fórmula del valor par.
Supongamos que\(U\) tiene la distribución binomial con parámetros\(m \in \N_+\) y\(p \in [0, 1]\),\(V\) tiene la distribución binomial con parámetros\(n \in \N_+\) y\(q \in [0, 1]\), y eso\(U\) y\(V\) son independientes.
- Si\(p = q\) entonces\(U + V\) tiene la distribución binomial con parámetros\(m + n\) y\(p\).
- Si\(p \ne q\) entonces\(U + V\) no tiene una distribución binomial.
Prueba
Del resultado para sumas de variables independientes y el PGF de la distribución binomial, nótese que la función generadora de probabilidad de\(U + V\) es\(P(t) = (1 - p + p t)^m (1 - q + q t)^n\) para\(t \in \R\).
- Si\( p = q \) entonces\( U + V \) tiene PGF\( P(t) = (1 - p + p t)^{m + n} \), que es el PGF de la distribución binomial con parámetros\( m + n \) y\( p \).
- Por otro lado, si\( p \ne q \), el PGF\( P \) no tiene la forma funcional de un PGF binomial.
Supongamos ahora eso\( p \in (0, 1] \). El número\( N \) de ensayos del primer éxito en la secuencia de ensayos de Bernoulli tiene la distribución geométrica\( \N_+ \) con parámetro éxito\( p \). La función de densidad de probabilidad\( h \) viene dada por\[h(n) = p (1 - p)^{n-1}, \quad n \in \N_+\] La distribución geométrica se estudia con más detalle en el capítulo sobre los ensayos de Bernoulli.
Dejar\(Q\) denotar la probabilidad que genera la función de\(N\). Entonces
- \(Q(t) = \frac{p t}{1 - (1 - p)t}\)para\(-\frac{1}{1 - p} \lt t \lt \frac{1}{1 - p}\)
- \(\E\left[N^{(k)}\right] = k! \frac{(1 - p)^{k-1}}{p^k}\)para\( k \in \N \)
- \(\E(N) = \frac{1}{p}\)
- \(\var(N) = \frac{1 - p}{p^2}\)
- \(\P(N \text{ is even}) = \frac{1 - p}{2 - p}\)
Prueba
- Usando la fórmula para la suma de una serie geométrica,\[ Q(t) = \sum_{n=1}^\infty (1 - p)^{n-1} p t^n = p t \sum_{n=1}^\infty [(1 - p) t]^{n-1} = \frac{p t}{1 - (1 - p) t}, \quad \left|(1 - p) t\right| \lt 1 \]
- La diferenciación repetida da\( H^{(k)}(t) = k! p (1 - p)^{k-1} \left[1 - (1 - p) t\right]^{-(k+1)} \) y luego el resultado se desprende de la fórmula de inversión.
- Esto se desprende de (b) y la fórmula para la media.
- Esto se desprende de (b) y la fórmula para la varianza.
- Esto se deduce de la fórmula de valor par.
La probabilidad de que\( N \) sea incluso surge en el juego alternante de lanzamiento de monedas con dos jugadores.
La distribución de Poisson
Recordemos que la distribución de Poisson tiene la función de densidad de probabilidad\(f\) dada por\[ f(n) = e^{-a} \frac{a^n}{n!}, \quad n \in \N \] donde\(a \in (0, \infty)\) es un parámetro. La distribución de Poisson lleva el nombre de Simeon Poisson y es ampliamente utilizada para modelar el número de puntos aleatorios
en una región de tiempo o espacio; el parámetro es proporcional al tamaño de la región de tiempo o espacio. La distribución de Poisson se estudia con más detalle en el capítulo sobre el Proceso de Poisson.
Supongamos que\(N\) tiene distribución de Poisson con parámetro\(a \in (0, \infty)\). Dejar\(P_a\) denotar la probabilidad que genera la función de\(N\). Entonces
- \(P_a(t) = e^{a (t - 1)}\)para\(t \in \R\)
- \(\E\left[N^{(k)}\right] = a^k\)
- \(\E(N) = a\)
- \(\var(N) = a\)
- \(\P(N \text{ is even}) = \frac{1}{2}\left(1 + e^{-2 a}\right)\)
Prueba
- Usando la serie exponencial,\[ P_a(t) = \sum_{n=0}^\infty e^{-a} \frac{a^n}{n!} t^n = e^{-a} \sum_{n=0}^\infty \frac{(a t)^n}{n!} = e^{-a} e^{a t}, \quad t \in \R \]
- La diferenciación repetida da\( P_a^{(k)}(t) = e^{a (t - 1)} a^k \), por lo que el resultado se desprende de la fórmula de inversión.
- Esto se desprende de (b) y la fórmula para la media.
- Esto se desprende de (b) y la fórmula para la varianza.
- Esto se deduce de la fórmula de valor par.
La familia de distribuciones Poisson está cerrada con respecto a sumas de variables independientes, una propiedad muy importante.
Supongamos que\(X, \, Y\) tienen distribuciones de Poisson con parámetros\(a, \, b \in (0, \infty)\), respectivamente, y eso\(X\) y\(Y\) son independientes. Después\(X + Y\) tiene la distribución de Poisson con parámetro\(a + b\).
Prueba
En la notación del resultado anterior, nótese que\( P_a P_b = P_{a+b} \).
La función de distribución correcta de la distribución de Poisson no tiene una expresión simple de forma cerrada. El siguiente ejercicio da un límite superior.
Supongamos que\(N\) tiene la distribución de Poisson con parámetro\(a \gt 0\). Entonces\[ \P(N \ge n) \le e^{n - a} \left(\frac{a}{n}\right)^n, \quad n \gt a \]
Prueba
El PGF de\( N \) es\( P(t) = e^{a (t - 1)} \) y por lo tanto el MGF es\( P\left(e^t\right) = \exp\left(a e^t - a\right) \). Desde los límites de Chernov tenemos\[ \P(N \ge n) \le e^{-t n} \exp\left(a e^t - a\right) = \exp\left(a e^t - a - tn\right) \] Si\( n \gt a \) la expresión de la derecha se minimiza cuando\( t = \ln(n / a) \). Sustituir da el límite superior.
El siguiente teorema da un importante resultado de convergencia que se explora con más detalle en el capítulo sobre el proceso de Poisson.
Supongamos que\( p_n \in (0, 1) \) para\( n \in \N_+ \) y que\( n p_n \to a \in (0, \infty) \) como\( n \to \infty \). Entonces la distribución binomial con parámetros\( n \) y\( p_n \) converge a la distribución de Poisson con parámetro\( a \) as\( n \to \infty \).
Prueba
Dejar\(P_n\) denotar la función generadora de probabilidad de la distribución binomial con parámetros\(n\) y\(p_n\). Del PGF de la distribución binomial tenemos\[ P_n(t) = \left[1 + p_n (t - 1)\right]^n = \left[1 + \frac{n p_n (t - 1)}{n}\right]^n, \quad t \in \R\] Usando un famoso teorema a partir del cálculo,\( P_n(t) \to e^{a (t - 1)} \) como\( n \to \infty \). Pero este es el PGF de la distribución de Poisson con parámetro\( a \), por lo que el resultado se desprende del teorema de continuidad para PGF.
La distribución exponencial
Recordemos que la distribución exponencial es una distribución continua\([0, \infty)\) con función de densidad de probabilidad\(f\) dada por\[ f(t) = r e^{-r t}, \quad t \in (0, \infty) \] donde\(r \in (0, \infty)\) está el parámetro de tasa. Esta distribución es ampliamente utilizada para modelar tiempos de falla y otros tiempos aleatorios, y en particular gobierna el tiempo entre llegadas en el modelo de Poisson. La distribución exponencial se estudia con más detalle en el capítulo sobre el Proceso de Poisson.
Supongamos que\(T\) tiene la distribución exponencial con parámetro de tasa\(r \in (0, \infty)\) y vamos a\(M\) denotar la función de generación de momento de\(T\). Entonces
- \(M(s) = \frac{r}{r - s}\)para\(s \in (-\infty, r)\).
- \(\E(T^n) = n! / r^n\)para\(n \in \N\)
Prueba
- \( M(s) = \E\left(e^{s T}\right) = \int_0^\infty e^{s t} r e^{-r t} \, dt = \int_0^\infty r e^{(s - r) t} \, dt = \frac{r}{r - s} \)para\( s \lt r \).
- \( M^{(n)}(s) = \frac{r n!}{(r - s)^{n+1}} \)para\( n \in \N \)
Supongamos que\((T_1, T_2, \ldots)\) es una secuencia de variables aleatorias independientes, teniendo cada una la distribución exponencial con el parámetro rate\(r \in (0, \infty)\). Para\(n \in \N_+\), el momento que genera la función\( M_n \) de\(U_n = \sum_{i=1}^n T_i\) viene dada por\[ M_n(s) = \left(\frac{r}{r - s}\right)^n, \quad s \in (-\infty, r) \]
Prueba
Esto se desprende del resultado anterior y el resultado para sumas de variables independientes.
La variable aleatoria\(U_n\) tiene la distribución Erlang con el parámetro shape\(n\) y el parámetro rate\(r\), llamado así por Agner Erlang. Esta distribución gobierna la\( n \) hora de llegada en el modelo de Poisson. La distribución Erlang es un caso especial de la distribución gamma y se estudia con más detalle en el capítulo sobre el Proceso de Poisson.
Distribuciones Uniformes
Supongamos que\( a, \, b \in \R \) y\( a \lt b \). Recordemos que la distribución uniforme continua en el intervalo\( [a, b] \) tiene función de densidad de probabilidad\( f \) dada por\[ f(x) = \frac{1}{b - a}, \quad x \in [a, b] \] La distribución corresponde a seleccionar un punto al azar del intervalo. Las distribuciones uniformes continuas surgen en probabilidad geométrica y una variedad de otros problemas aplicados.
Supongamos que\(X\) se distribuye uniformemente en el intervalo\([a, b]\) y vamos a\(M\) denotar la función de generación de momento de\(X\). Entonces
- \(M(t) = \frac{e^{b t} - e^{a t}}{(b - a)t}\)si\( t \ne 0 \) y\( M(0) = 1 \)
- \(\E\left(X^n\right) = \frac{b^{n+1} - a^{n + 1}}{(n + 1)(b - a)}\)para\(n \in \N\)
Prueba
- \( M(t) = \int_a^b e^{t x} \frac{1}{b - a} \, dx = \frac{e^{b t} - e^{a t}}{(b - a)t}\)si\( t \ne 0 \). Trivialmente\( M(0) = 1 \)
- Este es un caso en el que el MGF no es útil, y es mucho más fácil calcular los momentos directamente:\( \E\left(X^n\right) = \int_a^b x^n \frac{1}{b - a} \, dx = \frac{b^{n+1} - a^{n + 1}}{(n + 1)(b - a)} \)
Supongamos que\((X, Y)\) se distribuye uniformemente sobre el triángulo\(T = \{(x, y) \in \R^2: 0 \le x \le y \le 1\}\). Calcular cada uno de los siguientes:
- La función generadora de momento conjunto de\((X, Y)\).
- El momento que genera la función de\(X\).
- El momento que genera la función de\(Y\).
- El momento que genera la función de\(X + Y\).
Contestar
- \(M(s, t) = 2 \frac{e^{s+t} - 1}{s (s + t)} - 2 \frac{e^t - 1}{s t}\)si\( s \ne 0, \; t \ne 0\). \( M(0, 0) = 1 \)
- \(M_1(s) = 2 \left(\frac{e^2}{s^2} - \frac{1}{s^2} - \frac{1}{s}\right)\)si\(s \ne 0\). \( M_1(0) = 1 \)
- \(M_2(t) = 2 \frac{t e^t - e^t + 1}{t^2}\)si\( t \ne 0\). \( M_2(0) = 1 \)
- \(M_+(t) = \frac{e^{2 t} - 1}{t^2} - 2 \frac{e^t - 1}{t^2}\)si\(t \ne 0\). \( M_+(0) = 1 \)
Una distribución bivariada
Supongamos que\( (X, Y) \) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = x + y\) for\((x, y) \in [0, 1]^2\). Calcular cada uno de los siguientes:
- La función generadora de momento conjunto\( (X, Y) \).
- El momento que genera la función de\(X\).
- El momento que genera la función de\(Y\).
- El momento que genera la función de\(X + Y\).
Contestar
- \(M(s, t) = \frac{e^{s+t}(-2 s t + s + t) + e^s(s t - s - t) + s + t}{s^2 t^2}\)si\(s \ne 0, \, t \ne 0\). \( M(0, 0) = 1 \)
- \(M_1(s) = \frac{3 s e^2 - 2 e^2 - s + 2}{2 s^2}\)si\(s \ne 0\). \( M_1(0) = 1 \)
- \(M_2(t) = \frac{3 t e^t - 2 e^t - t + 2}{2 t^2}\)si\(t \ne 0\). \( M_2(0) = 1 \)
- \(M_+(t) = \frac{[e^{2 t}(1 - t) + e^t (t - 2) + 1]}{t^3}\)si\(t \ne 0\). \( M_+(0) = 1 \)
La distribución normal
Recordemos que la distribución normal estándar es una distribución continua\(\R) with probability density function \(\phi\) dada por las distribuciones\[ \phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2}, \quad z \in \R \] normales son ampliamente utilizadas para modelar medidas físicas sujetas a pequeños errores aleatorios y se estudian con más detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(Z\) tiene la distribución normal estándar y vamos a\(M\) denotar la función de generación de momento de\(Z\). Entonces
- \(M(t) = e^{\frac{1}{2} t^2}\)para\(t \in \R\)
- \(\E\left(Z^n\right) = 1 \cdot 3 \cdots (n - 1)\)si\( n \) es par y\(\E\left(Z^n\right) = 0\) si\(n\) es impar.
Prueba
- Primero,\[ M(t) = \E\left(e^{t Z}\right) = \int_{-\infty}^\infty e^{t z} \frac{1}{\sqrt{2 \pi}} e^{-z^2 / 2} \, dz = \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp\left(-\frac{z^2}{2} + t z\right) \, dz \] Completando el cuadrado en\( z \) da\(\exp\left(-\frac{z^2}{2} + t z\right) = \exp\left[\frac{1}{2} t^2 - \frac{1}{2}(z - t)^2 \right] = e^{\frac{1}{2} t^2} \exp\left[-\frac{1}{2} (z - t)^2\right] \). de ahí\[ M(t) = e^{\frac{1}{2} t^2} \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp\left[-\frac{1}{2} (z - t)^2\right] \, dz = e^{\frac{1}{2} t^2} \] porque la función de\( z \) en la última integral es la función de densidad de probabilidad para la distribución normal con media\( t \) y varianza 1.
- Tenga en cuenta que\( M^\prime(t) = t M(t) \). Así, la diferenciación repetida da\( M^{(n)}(t) = p_n(t) M(t) \) para\( n \in \N \), donde\( p_n \) es un polinomio de grado\( n \) satisfactorio\( p_{n+1}^\prime(t) = t p_n(t) + p_n^\prime(t) \). Ya que\( p_0 = 1 \), es fácil ver que solo\( p_n \) tiene términos pares o sólo impares, dependiendo de si\( n \) es par o impar, respectivamente. Por lo tanto,\( \E\left(X^n\right) = p_n(0) \). Esto es 0 si\( n \) es impar, y es el término constante\( 1 \cdot 3 \cdots (n - 1) \) si\( n \) es par. Por supuesto, también podemos ver que los momentos de orden impar deben ser 0 por simetría.
De manera más general, para\(\mu \in \R\) y\(\sigma \in (0, \infty)\), recordar que la distribución normal con media\(\mu\) y desviación estándar\(\sigma\) es una distribución continua\(\R\) con función de densidad de probabilidad\( f \) dada por\[ f(x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp\left[-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2\right], \quad x \in \R \] Además, si\( Z \) tiene la distribución normal estándar , luego\( X = \mu + \sigma Z \) tiene la distribución normal con media\( \mu \) y desviación estándar\( \sigma \). Así, podemos encontrar fácilmente la función generadora de momento de\( X \):
Supongamos que\(X\) tiene la distribución normal con media\(\mu\) y desviación estándar\(\sigma\). La función de generación de momento de\(X\) es\[M(t) = \exp\left(\mu t + \frac{1}{2} \sigma^2 t^2\right), \quad t \in \R\]
Prueba
Esto sigue fácilmente el resultado anterior y el resultado para transformaciones lineales:\( X = \mu + \sigma Z \) donde\( Z \) tiene la distribución normal estándar. De ahí\[ M(t) = \E\left(e^{t X}\right) = e^{\mu t} \E\left(e^{\sigma t Z}\right) = e^{\mu t} e^{\frac{1}{2} \sigma^2 t ^2}, \quad t \in \R \]
Así que la familia normal de distribuciones en transformaciones cerradas bajo escala de ubicación. La familia también se cierra con respecto a sumas de variables independientes:
Si\(X\) y\(Y\) son independientes, las variables aleatorias normalmente distribuidas entonces\(X + Y\) tienen una distribución normal.
Prueba
Supongamos que\( X \) tiene la distribución normal con media\( \mu \in \R \) y desviación estándar\( \sigma \in (0, \infty) \), y que\( Y \) tiene la distribución normal con media\( \nu \in \R \) y desviación estándar\( \tau \in (0, \infty) \). Por (14), el MGF de\( X + Y \) es el\[ M_{X+Y}(t) = M_X(t) M_Y(t) = \exp\left(\mu t + \frac{1}{2} \sigma^2 t^2\right) \exp\left(\nu t + \frac{1}{2} \tau^2 t^2\right) = \exp\left[(\mu + \nu) t + \frac{1}{2}\left(\sigma^2 + \tau^2\right) t^2 \right] \] que reconocemos como el MGF de la distribución normal con media\( \mu + \nu \) y varianza\( \sigma^2 + \tau^2 \). Por supuesto, eso ya lo sabíamos\( \E(X + Y) = \E(X) + \E(Y) \), y desde\( X \) y\( Y \) somos independientes,\( \var(X + Y) = \var(X) + \var(Y) \), por lo que la nueva información es que la distribución también es normal.
La distribución de Pareto
Recordemos que la distribución de Pareto es una distribución continua\([1, \infty) with probability density function \(f\) dada por\[ f(x) = \frac{a}{x^{a + 1}}, \quad x \in [1, \infty) \] donde\(a \in (0, \infty)\) está el parámetro shape. La distribución de Pareto lleva el nombre de Vilfredo Pareto. Se trata de una distribución de cola pesada que es ampliamente utilizada para modelar variables financieras como el ingreso. La distribución de Pareto se estudia con más detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(X\) tiene la distribución de Pareto con el parámetro shape\( a \), y vamos a\( M \) denotar la función de generación de momento de\( X \). Entonces
- \(\E\left(X^n\right) = \frac{a}{a - n}\)si\(n \lt a\) y\(\E\left(X^n\right) = \infty\) si\(n \ge a\)
- \(M(t) = \infty\)para\(t \gt 0\)
Prueba
- Ya hemos visto este cómputo antes. \( \E\left(X^n\right) = \int_1^\infty x^n \frac{a}{x^{a+1}} \, dx = \int_1^\infty x^{n - a - 1} \, dx \). La integral evalúa a\( \frac{a}{a - n} \) si\( n \lt a \) y\( \infty \) si\( n \ge a \).
- Esto se desprende de la parte a). Ya que\( X \ge 1 \),\( M(t) \) está aumentando en\( t \). Por lo tanto\( M(t) \le 1 \) si\( t \lt 0 \). Si\( M(t) \lt \infty \) para algunos\( t \gt 0 \), entonces\( M(t) \) sería finito para\( t \) en un intervalo abierto alrededor de 0, en cuyo caso\( X \) tendría momentos finitos de todos los órdenes. Por supuesto, también es fácil ver directamente desde la integral que\( M(t) = \infty \) para\( t \gt 0 \)
Por otro lado, como todas las distribuciones en adelante\( \R \), la distribución de Pareto tiene una función característica. Sin embargo, la función característica de la distribución de Pareto no tiene una forma simple y cerrada.
La distribución de Cauchy
Recordemos que la distribución (estándar) de Cauchy es una distribución continua\(\R\) con la función de densidad de probabilidad\(f\) dada por\[ f(x) = \frac{1}{\pi \left(1 + x^2\right)}, \quad x \in \R \] y se llama así por Augustin Cauchy. La distribución de Cauch se estudia con más generalidad en el capítulo sobre Distribuciones Especiales. La gráfica de\(f\) es conocida como la Bruja de Agnesi, llamada así por Maria Agnesi.
Supongamos que\( X \) tiene la distribución estándar de Cauchy, y vamos a\(M\) denotar la función de generación de momento de\(X\). Entonces
- \(\E(X)\)no existe.
- \(M(t) = \infty\)para\(t \ne 0\).
Prueba
- Ya hemos visto este cómputo antes. \( \int_a^\infty \frac{x}{\pi (1 + x^2)} \, dx = \infty \)y\( \int_{-\infty}^a \frac{x}{\pi (1 + x^2)} \, dx = -\infty \) para cada\( a \in \R \), así\( \int_{-\infty}^\infty \frac{x}{\pi (1 + x^2)} \, dx \) no existe.
- Tenga en cuenta que\( \int_0^\infty \frac{e^{t x}}{\pi (1 + x^2) } \, dx = \infty\) si\( t \ge 0 \) y\( \int_{-\infty}^0 \frac{e^{t x}}{\pi (1 + x^2)} \, dx = \infty \) si\( t \le 0 \).
Una vez más, todas las distribuciones\( \R \) tienen funciones características, y la distribución estándar de Cauchy tiene una particularmente simple.
Dejar\(\chi\) denotar la función característica de\(X\). Entonces\(\chi(t) = e^{-\left|t\right|}\) para\(t \in \R\).
Prueba
La prueba de este resultado requiere integrales de contorno en el plano complejo, y se da en la sección sobre la distribución de Cauchy en el capítulo sobre distribuciones especiales.
Contraejemplo
Para la distribución de Pareto, solo algunos de los momentos son finitos; así que por supuesto, la función de generación de momentos no puede ser finita en un intervalo de aproximadamente 0. Daremos ahora un ejemplo de una distribución para la que todos los momentos son finitos, sin embargo, la función de generación de momentos no es finita en ningún intervalo alrededor de 0. Además, veremos dos distribuciones diferentes que tienen los mismos momentos de todos los pedidos.
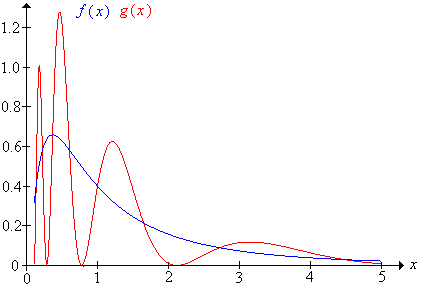
Supongamos que Z tiene la distribución normal estándar y let\(X = e^Z\). La distribución de\(X\) se conoce como la distribución lognormal (estándar). La distribución logarítmica normal se estudia en mayor generalidad en el capítulo sobre Distribuciones Especiales. Esta distribución tiene momentos finitos de todos los órdenes, pero función generadora de momento infinito.
\(X\)tiene la función de densidad de probabilidad\(f\) dada por\[ f(x) = \frac{1}{\sqrt{2 \pi} x} \exp\left(-\frac{1}{2} \ln^2(x)\right), \quad x \gt 0 \]
- \(\E\left(X^n\right) = e^{\frac{1}{2}n^2}\)para\(n \in \N\).
- \(\E\left(e^{t X}\right) = \infty\)para\(t \gt 0\).
Prueba
Utilizamos el teorema del cambio de variables. La transformación es\( x = e^z \) así que la transformación inversa es\( z = \ln x \) para\( x \in (0, \infty) \) y\( z \in \R \). Dejando\( \phi \) denotar el PDF de\( Z \), se deduce que el PDF de\( X \) es\( f(x) = \phi(z) \, dz / dx = \phi\left(\ln x\right) \big/ x \) para\( x \gt 0 \).
- Utilizamos la función de generación de momento de la distribución normal estándar dada anteriormente:\( \E\left(X^n\right) = \E\left(e^{n Z}\right) = e^{n^2 / 2}\).
- Tenga en cuenta que\[ \E\left(e^{t X}\right) = \E\left[\sum_{n=0}^\infty \frac{(t X)^n}{n!}\right] = \sum_{n=0}^\infty \frac{\E(X^n)}{n!} t^n = \sum_{n=0}^\infty \frac{e^{n^2 / 2}}{n!} t^n = \infty, \quad t \gt 0 \] El intercambio de valor esperado y suma se justifica ya que no\( X \) es negativo. Consulte la sección avanzada sobre propiedades de la integral en el capítulo sobre Distribuciones para más detalles.
A continuación construimos una distribución diferente con los mismos momentos que\( X \).
Dejar\(h\) ser la función definida por\(h(x) = \sin\left(2 \pi \ln x \right)\) for\(x \gt 0\) y let\(g\) ser la función definida por\(g(x) = f(x)\left[1 + h(x)\right]\) for\(x \gt 0\). Entonces
- \(g\)es una función de densidad de probabilidad.
- Si\( Y \) tiene función de densidad de probabilidad\( g \) entonces\(\E\left(Y^n\right) = e^{\frac{1}{2} n^2}\) para\(n \in \N\)
Prueba