4.5: Covarianza y Correlación
- Page ID
- 151941
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recordemos que al tomar el valor esperado de diversas transformaciones de una variable aleatoria, podemos medir muchas características interesantes de la distribución de la variable. En esta sección, estudiaremos un valor esperado que mide un tipo especial de relación entre dos variables de valor real. Esta relación es muy importante tanto en probabilidad como estadística.
Teoría Básica
Definiciones
Como es habitual, nuestro punto de partida es un experimento aleatorio modelado por un espacio de probabilidad\((\Omega, \mathscr F, \P)\). A menos que se indique lo contrario, asumimos que existen todos los valores esperados mencionados en esta sección. Supongamos ahora que\(X\) y\(Y\) son variables aleatorias de valor real para el experimento (es decir, definidas en el espacio de probabilidad) con medias\(\E(X)\),\(\E(Y)\) y varianzas\(\var(X)\)\(\var(Y)\), respectivamente.
La covarianza de\((X, Y)\) se define por\[ \cov(X, Y) = \E\left(\left[X - \E(X)\right]\left[Y - \E(Y)\right]\right) \] y, asumiendo que las varianzas son positivas, la correlación de\( (X, Y)\) se define por\[ \cor(X, Y) = \frac{\cov(X, Y)}{\sd(X) \sd(Y)} \]
- Si\(\cov(X, Y) \gt 0\) entonces\(X\) y\(Y\) están correlacionados positivamente.
- Si\(\cov(X, Y) \lt 0\) entonces\(X\) y\(Y\) están correlacionados negativamente.
- Si\(\cov(X, Y) = 0\) entonces\(X\) y no\(Y\) están correlacionados.
La correlación es una versión escalada de la covarianza; tenga en cuenta que los dos parámetros siempre tienen el mismo signo (positivo, negativo o 0). Obsérvese también que la correlación es adimensional, ya que el numerador y denominador tienen las mismas unidades físicas, es decir, el producto de las unidades de\(X\) y\(Y\).
Como sugieren estos términos, la covarianza y la correlación miden cierto tipo de dependencia entre las variables. Uno de nuestros objetivos es una comprensión más profunda de esta dependencia. Como inicio, tenga en cuenta que\(\left(\E(X), \E(Y)\right)\) es el centro de la distribución conjunta de\((X, Y)\), y las líneas verticales y horizontales a través de este punto\(\R^2\) se separan en cuatro cuadrantes. La función\((x, y) \mapsto \left[x - \E(X)\right]\left[y - \E(Y)\right]\) es positiva en el primer y tercer cuadrantes y negativa en el segundo y cuarto.
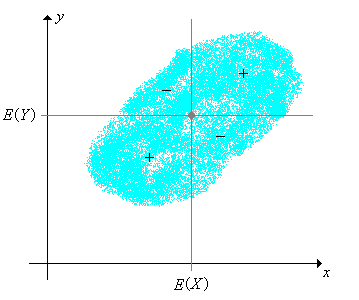
Propiedades de la Covarianza
Los siguientes teoremas dan algunas propiedades básicas de covarianza. La principal herramienta que necesitaremos es el hecho de que el valor esperado es una operación lineal. Otras propiedades importantes se derivarán a continuación, en la subsección sobre el mejor predictor lineal. Como es habitual, asegúrate de probar las pruebas tú mismo antes de leer las que aparecen en el texto. Una vez más, asumimos que las variables aleatorias se definen en el espacio muestral común, son de valor real y que existen los valores esperados indicados (como números reales).
Nuestro primer resultado es una fórmula que es mejor que la definición para fines computacionales, pero que da menos perspicacia.
\(\cov(X, Y) = \E(X Y) - \E(X) \E(Y)\).
Prueba
Dejar\( \mu = \E(X) \) y\( \nu = \E(Y) \). Entonces
\[ \cov(X, Y) = \E\left[(X - \mu)(Y - \nu)\right] = \E(X Y - \mu Y - \nu X + \mu \nu) = \E(X Y) - \mu \E(Y) - \nu \E(X) + \mu \nu = \E(X Y) - \mu \nu \]De (2), vemos eso\(X\) y no\(Y\) están correlacionados si y solo si\(\E(X Y) = \E(X) \E(Y)\), así que aquí hay un corolario simple pero importante:
Si\(X\) y\(Y\) son independientes, entonces no están correlacionados.
Prueba
Mostramos en la Sección 1 que si\(X\) y\(Y\) son indepedientes entonces\(\E(X Y) = \E(X) \E(Y)\).
Sin embargo, lo contrario falla con una pasión: el ejercicio (31) da un ejemplo de dos variables que están funcionalmente relacionadas (la forma más fuerte de dependencia), pero no correlacionadas. Los ejercicios computacionales dan también otros ejemplos de variables dependientes pero no correlacionadas. Obsérvese también que si una de las variables tiene media 0, entonces la covarianza es simplemente el producto esperado.
Trivialmente, la covarianza es una operación simétrica.
\(\cov(X, Y) = \cov(Y, X)\).
Como su nombre indica, la covarianza generaliza la varianza.
\(\cov(X, X) = \var(X)\).
Prueba
Vamos\( \mu = \E(X) \). Entonces\( \cov(X, X) = \E\left[(X - \mu)^2\right] = \var(X) \).
La covarianza es una operación lineal en el primer argumento, si el segundo argumento es fijo.
Si\(X\),\(Y\),\(Z\) son variables aleatorias, y\(c\) es una constante, entonces
- \(\cov(X + Y, Z) = \cov(X, Z) + \cov(Y, Z)\)
- \(\cov(c X, Y) = c \, \cov(X, Y)\)
Prueba
Utilizamos la fórmula computacional en (2)
- \ begin {align}\ cov (X + Y, Z) & =\ E\ izquierda [(X + Y) Z\ derecha] -\ E (X + Y)\ E (Z) =\ E (X Z + Y Z) -\ izquierda [\ E (X) +\ E (Y)\ derecha]\ E (Z)\ & =\ izquierda [\ E (X Z) -\ E (X)\ E (Z)\ derecha] +\ izquierda [\ E (Y Z) -\ E (Y)\ E (Z)\ derecha] =\ cov (X, Z) +\ cov (Y, Z)\ final {align}
- \[ \cov(c X, Y) = \E(c X Y) - \E(c X) \E(Y) = c \E(X Y) - c \E(X) \E(Y) = c [\E(X Y) - \E(X) \E(Y) = c \, \cov(X, Y) \]
Por simetría, la covarianza es también una operación lineal en el segundo argumento, con el primer argumento fijo. Así, el operador de covarianza es bi-lineal. La versión general de esta propiedad se da en el siguiente teorema.
Supongamos que\((X_1, X_2, \ldots, X_n)\) y\((Y_1, Y_2, \ldots, Y_m)\) son secuencias de variables aleatorias,\((a_1, a_2, \ldots, a_n)\) y eso y\((b_1, b_2, \ldots, b_m)\) son constantes. Entonces\[ \cov\left(\sum_{i=1}^n a_i \, X_i, \sum_{j=1}^m b_j \, Y_j\right) = \sum_{i=1}^n \sum_{j=1}^m a_i \, b_j \, \cov(X_i, Y_j) \]
El siguiente resultado muestra cómo se cambia la covarianza bajo una transformación lineal de una de las variables. Este es simplemente un caso especial de las propiedades básicas, pero vale la pena señalar.
Si\( a, \, b \in \R \) entonces\(\cov(a + bX, Y) = b \, \cov(X, Y)\).
Prueba
Una constante es independiente de cualquier variable aleatoria. De ahí\( \cov(a + b X, Y) = \cov(a, Y) + b \, \cov(X, Y) = b \, \cov(X, Y) \).
Por supuesto, por simetría, la misma propiedad se sostiene en el segundo argumento. Armando los dos tenemos eso si\( a, \, b, \, c, \, d \in \R \) entonces\( \cov(a + b X, c + d Y) = b d \, \cov(X, Y) \).
Propiedades de Correlación
A continuación estableceremos algunas propiedades básicas de correlación. La mayoría de estos se derivan fácilmente de las correspondientes propiedades de covarianza anteriores. Suponemos que\(\var(X) \gt 0\) y\(\var(Y) \gt 0\), de manera que las variables aleatorias son realmente aleatorias y de ahí que la correlación esté bien definida.
La correlación entre\(X\) y\(Y\) es la covarianza de las puntuaciones estándar correspondientes:\[ \cor(X, Y) = \cov\left(\frac{X - \E(X)}{\sd(X)}, \frac{Y - \E(Y)}{\sd(Y)}\right) = \E\left(\frac{X - \E(X)}{\sd(X)} \frac{Y - \E(Y)}{\sd(Y)}\right) \]
Prueba
A partir de las definiciones y la linealidad del valor esperado,\[ \cor(X, Y) = \frac{\cov(X, Y)}{\sd(X) \sd(Y)} = \frac{\E\left(\left[X - \E(X)\right]\left[Y - \E(Y)\right]\right)}{\sd(X) \sd(Y)} = \E\left(\frac{X - \E(X)}{\sd(X)} \frac{Y - \E(Y)}{\sd(Y)}\right) \] Dado que las puntuaciones estándar tienen media 0, esta es también la covarianza de las puntuaciones estándar.
Esto demuestra nuevamente que la correlación es adimensional, ya que por supuesto, las puntuaciones estándar son adimensionales. Además, la correlación es simétrica:
\(\cor(X, Y) = \cor(Y, X)\).
Bajo una transformación lineal de una de las variables, la correlación no cambia si la pendiente es positiva y cambia de signo si la pendiente es negativa:
Si\(a, \, b \in \R\) y\( b \ne 0 \) entonces
- \(\cor(a + b X, Y) = \cor(X, Y)\)si\(b \gt 0\)
- \(\cor(a + b X, Y) = - \cor(X, Y)\)si\(b \lt 0\)
Prueba
Dejar\( Z \) denotar la puntuación estándar de\( X \). Si\( b \gt 0 \), la puntuación estándar de también\( a + b X \) es\( Z \). Si\( b \lt 0 \), la puntuación estándar de\( a + b X \) es\( -Z \). De ahí que el resultado se deduce del resultado anterior para las puntuaciones estándar.
Este resultado refuerza el hecho de que la correlación es una medida estandarizada de asociación, ya que multiplicar la variable por una constante positiva equivale a un cambio de escala, y agregar un contant a una variable equivale a un cambio de ubicación. Por ejemplo, en los datos de Challenger, las variables subyacentes son la temperatura al momento del lanzamiento (en grados Fahrenheit) y la erosión de la junta tórica (en milímetros). La correlación entre estas dos variables es de fundamental importancia. Si decidimos medir la temperatura en grados Celsius y la erosión de la junta tórica en pulgadas, la correlación no cambia. Por supuesto, la misma propiedad se mantiene en el segundo argumento, así que si\( a, \, b, \, c, \, d \in \R \) con\( b \ne 0 \) y\( d \ne 0 \), entonces\( \cor(a + b X, c + d Y) = \cor(X, Y) \) si\( b d \gt 0 \) y\( \cor(a + b X, c + d Y) = -\cor(X, Y) \) si\( b d \lt 0 \).
Las propiedades más importantes de covarianza y correlación surgirán de nuestro estudio del mejor predictor lineal a continuación.
La varianza de una suma
Ahora mostraremos que la varianza de una suma de variables es la suma de las covarianzas por pares. Este resultado es muy útil ya que muchas variables aleatorias con distribuciones especiales se pueden escribir como sumas de variables aleatorias más simples (ver en particular la distribución binomial y la distribución hipergeométrica a continuación).
Si\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias de valor real entonces\[ \var\left(\sum_{i=1}^n X_i\right) = \sum_{i=1}^n \sum_{j=1}^n \cov(X_i, X_j) = \sum_{i=1}^n \var(X_i) + 2 \sum_{\{(i, j): i \lt j\}} \cov(X_i, X_j) \]
Prueba
A partir de la propiedad de varianza on (5), y la propiedad lineal (7),\[ \var\left(\sum_{i=1}^n X_i\right) = \cov\left(\sum_{i=1}^n X_i, \sum_{j=1}^n X_j\right) = \sum_{i=1}^j \sum_{j=1}^n \cov(X_i, X_j) \] La segunda expresión sigue ya que\( \cov(X_i, X_i) = \var(X_i) \) para cada uno\( i \) y\( \cov(X_i, X_j) = \cov(X_j, X_i) \) para\( i \ne j \) por la propiedad de simetría (4)
Tenga en cuenta que la varianza de una suma puede ser mayor, menor o igual a la suma de las varianzas, dependiendo de los términos de covarianza pura. Como caso especial de (12), cuando\(n = 2\), tenemos\[ \var(X + Y) = \var(X) + \var(Y) + 2 \, \cov(X, Y) \] El siguiente corolario es muy importante.
Si\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias de valor real, no correlacionadas por pares, entonces\[ \var\left(\sum_{i=1}^n X_i\right) = \sum_{i=1}^n \var(X_i) \]
Prueba
Esto se deduce inmediatamente de (12), ya que\( \cov(X_i, X_j) = 0 \) para\( i \ne j \).
Tenga en cuenta que el último resultado se mantiene, en particular, si las variables aleatorias son independientes. Cerramos esta discusión con un par de corolarios menores.
Si\(X\) y\(Y\) son variables aleatorias de valor real entonces\(\var(X + Y) + \var(X - Y) = 2 \, [\var(X) + \var(Y)]\).
Prueba
De (12),\[ \var(X + Y) = \var(X) + \var(Y) + 2 \cov(X, Y) \] Similarmente,\[ \var(X - Y) = \var(X) + \var(-Y) + 2 \cov(X, - Y) = \var(X) + \var(Y) - 2 \cov(X, Y) \] Sumando da el resultado.
Si\(X\) y\(Y\) son variables aleatorias de valor real con\(\var(X) = \var(Y)\) entonces\(X + Y\) y no\(X - Y\) están correlacionadas.
Muestras Aleatorias
En los siguientes ejercicios, supongamos que\((X_1, X_2, \ldots)\) se trata de una secuencia de variables aleatorias independientes, de valor real, con una distribución común que tiene media\(\mu\) y desviación estándar\(\sigma \gt 0\). En términos estadísticos, las variables forman una muestra aleatoria a partir de la distribución común.
Para\(n \in \N+\), vamos\(Y_n = \sum_{i=1}^n X_i\).
- \(\E\left(Y_n\right) = n \mu\)
- \(\var\left(Y_n\right) = n \sigma^2\)
Prueba
- Esto se desprende de la propiedad aditiva de valor esperado.
- Esto se desprende de la propiedad aditiva de varianza (`(13) para variables independientes
Para\(n \in \N_+\), vamos\(M_n = Y_n \big/ n = \frac{1}{n} \sum_{i=1}^n X_i\), así que esa\(M_n\) es la media muestral de\((X_1, X_2, \ldots, X_n)\).
- \(\E\left(M_n\right) = \mu\)
- \(\var\left(M_n\right) = \sigma^2 / n\)
- \(\var\left(M_n\right) \to 0\)como\(n \to \infty\)
- \(\P\left(\left|M_n - \mu\right| \gt \epsilon\right) \to 0\)como\(n \to \infty\) para cada\(\epsilon \gt 0\).
Prueba
- Esto se desprende de la parte (a) de la (16) y la propiedad de escalado del valor esperado.
- Esto se desprende de la parte (b) de la (16) y la propiedad de escalado de la varianza.
- Esto es una consecuencia inmediata de (b).
- Esto se desprende de (c) y la desigualdad de Chebyshev:\( \P\left(\left|M_n - \mu\right| \gt \epsilon\right) \le \var(M_n) \big/ \epsilon^2 \to 0 \) como\( n \to \infty \)
La parte (c) de (17) significa que\(M_n \to \mu\) como\(n \to \infty\) en el cuadrado medio. La parte (d) significa que\(M_n \to \mu\) como\(n \to \infty\) en probabilidad. Ambas son versiones de la débil ley de los grandes números, uno de los teoremas fundamentales de la probabilidad.
La puntuación estándar de la suma\( Y_n \) y la puntuación estándar de la media muestral\( M_n \) son las mismas:\[ Z_n = \frac{Y_n - n \, \mu}{\sqrt{n} \, \sigma} = \frac{M_n - \mu}{\sigma / \sqrt{n}} \]
- \(\E(Z_n) = 0\)
- \(\var(Z_n) = 1\)
Prueba
La igualdad de la puntuación estándar de\( Y_n \) y de\( Z_n \) es resultado del álgebra simple. Pero recordemos de manera más general que la puntuación estándar de una variable no cambia por una transformación lineal de la variable con pendiente positiva (una transformación ubicación-escala de la distribución). Por supuesto, las partes (a) y (b) son ciertas para cualquier puntaje estándar.
El teorema del límite central, el otro teorema fundamental de probabilidad, establece que la distribución de\(Z_n\) converge a la distribución normal estándar como\(n \to \infty\).
Eventos
Si\(A\) y\(B\) son eventos en nuestro experimento aleatorio entonces la covarianza y correlación de\(A\) y\(B\) se definen como la covarianza y correlación, respectivamente, de sus variables aleatorias indicadoras.
Si\(A\) y\(B\) son eventos, definir\(\cov(A, B) = \cov(\bs 1_A, \bs 1_B)\) y\(\cor(A, B) = \cor(\bs 1_A, \bs 1_B)\). Equivalentemente,
- \(\cov(A, B) = \P(A \cap B) - \P(A) \P(B)\)
- \(\cor(A, B) = \left[\P(A \cap B) - \P(A) \P(B)\right] \big/ \sqrt{\P(A)\left[1 - \P(A)\right] \P(B)\left[1 - \P(B)\right]}\)
Prueba
Recordemos que si\( X \) es una variable indicadora con\( \P(X = 1) = p \), entonces\( \E(X) = p \) y\( \var(X) = p (1 - p) \). Además, si\( X \) y\( Y \) son variables indicadoras entonces\( X Y \) es una variable indicadora y\( \P(X Y = 1) = \P(X = 1, Y = 1) \). Los resultados luego se derivan de las definiciones.
En particular, tenga en cuenta que\(A\) y\(B\) están correlacionados positivamente, correlacionados negativamente o independientes, respectivamente (como se define en la sección sobre probabilidad condicional) si y solo si las variables indicadoras de\(A\) y\(B\) están correlacionadas positivamente, correlacionadas negativamente, o no correlacionados, tal y como se define en esta sección.
Si\(A\) y\(B\) son eventos entonces
- \(\cov(A, B^c) = -\cov(A, B)\)
- \(\cov(A^c, B^c) = \cov(A, B)\)
Prueba
Estos resultados se derivan de la propiedad lineal (7) y el hecho de que eso\( \bs 1_{A^c} = 1 - \bs 1_A \).
Si\( A \) y\( B \) son eventos con\(A \subseteq B\) entonces
- \(\cov(A, B) = \P(A)[1 - \P(B)]\)
- \(\cor(A, B) = \sqrt{\P(A)\left[1 - \P(B)\right] \big/ \P(B)\left[1 - \P(A)\right]}\)
Prueba
Estos resultados se derivan de (19), ya que\( A \cap B = A \).
En el lenguaje del experimento,\( A \subseteq B \) significa que eso\( A \) implica\( B \). En tal caso, los eventos están correlacionados positivamente, no es sorprendente.
El mejor predictor lineal
¿Qué función lineal de\(X\) (es decir, una función de la forma\( a + b X \) donde\( a, \, b \in \R \)) está más cercana\(Y\) en el sentido de minimizar el error cuadrático medio? La pregunta es fundamentalmente importante en el caso donde la variable aleatoria\(X\) (la variable predictora) es observable y la variable aleatoria\(Y\) (la variable de respuesta) no lo es. La función lineal se puede utilizar para estimar a\(Y\) partir de un valor observado de\(X\). Además, la solución tendrá el beneficio agregado de mostrar que la covarianza y la correlación miden la relación lineal entre\(X\) y\(Y\). Para evitar casos triviales, supongamos que\(\var(X) \gt 0\) y\(\var(Y) \gt 0\), para que las variables aleatorias sean realmente aleatorias. La solución a nuestro problema resulta ser la función lineal de\( X \) con el mismo valor esperado que\( Y \), y cuya covarianza con\( X \) es la misma que la de\( Y \).
La variable aleatoria\(L(Y \mid X)\) definida de la siguiente manera es la única función lineal de\(X\) satisfacer las propiedades (a) y (b). \[ L(Y \mid X) = \E(Y) + \frac{\cov(X, Y)}{\var(X)} \left[X - \E(X)\right] \]
- \( \E\left[L(Y \mid X)\right] = \E(Y) \)
- \( \cov\left[X, L(Y \mid X) \right] = \cov(X, Y) \)
Prueba
Por la linealidad del valor esperado,\[ \E\left[L(Y \mid X)\right] = \E(Y) + \frac{\cov(X, Y)}{\var(X)} \left[\E(X) - \E(X)\right] = \E(Y) \] Next, por la linealidad de la covarianza y el hecho de que una constante es independiente (y por lo tanto no correlacionada) con cualquier variable aleatoria,\[ \cov\left[X, L(Y \mid X)\right] = \frac{\cov(X, Y)}{\var(X)} \cov(X, X) = \frac{\cov(X, Y)}{\var(X)} \var(X) = \cov(X, Y) \] Por el contrario, supongamos que\( U = a + b X \) satisface\(\E(U) = \E(Y)\) y\( \cov(X, U) = \cov(Y, U) \). Nuevamente utilizando la linealidad de la covarianza y la propiedad no correlacionada de las constantes, la segunda ecuación\( b \, \cov(X, X) = \cov(X, Y) \) lo da\( b = \cov(X, Y) \big/ \var(X) \). Entonces la primera ecuación da\( a = \E(Y) - b \E(X) \), entonces\( U = L(Y \mid X) \).
Obsérvese que en presencia de la parte (a), la parte (b) es equivalente a\( \E\left[X L(Y \mid X)\right] = \E(X Y) \). Aquí hay otra variación menor, pero una que será muy útil:\( L(Y \mid X) \) es la única función lineal de\( X \) con la misma media que\( Y \) y con la propiedad que no\( Y - L(Y \mid X) \) está correlacionada con cada función lineal de\( X \).
\( L(Y \mid X) \)es la única función lineal de\( X \) que satisface
- \( \E\left[L(Y \mid X)\right] = \E(Y) \)
- \( \cov\left[Y - L(Y \mid X), U\right] = 0 \)para cada función lineal\( U \) de\( X \).
Prueba
Por supuesto, la parte (a) es la misma que la parte (a) de (22). Supongamos que\( U = a + b X \) donde\( a, \, b \in \R \). A partir de las propiedades básicas de la covarianza y el resultado anterior,\[ \cov\left[Y - L(Y \mid X), U\right] = b \, \cov\left[Y - L(Y \mid X), X\right] = b \left(\cov(Y, X) - \cov\left[L(Y \mid X), X\right]\right) = 0 \] Por el contrario, supongamos que\( V \) es una función lineal de\( X \)\( \E(V) = \E(Y) \) y que y\( \cov(Y - V, U) = 0 \) para cada función lineal\( U \) de\( X \). Dejando\( U = X \) que\( \cov(Y - V, X) = 0 \) así lo tengamos\( \cov(V, X) = \cov(Y, X) \). De ahí\( V = L(Y \mid X) \) por (22).
La varianza de\( L(Y \mid X) \) y su covarianza con\( Y \) resultan ser la misma.
Propiedades adicionales de\( L(Y \mid X) \):
- \( \var\left[L(Y \mid X)\right] = \cov^2(X, Y) \big/ \var(X) \)
- \( \cov\left[L(Y \mid X), Y\right] = \cov^2(X, Y) \big/ \var(X) \)
Prueba
- A partir de las propiedades básicas de varianza,\[ \var\left[L(Y \mid X)\right] = \left[\frac{\cov(X, Y)}{\var(X)}\right]^2 \var(X) = \frac{\cov^2(X, Y)}{\var(X)} \]
- A partir de las propiedades básicas de covarianza,\[ \cov\left[L(Y \mid X), Y\right] = \frac{\cov(X, Y)}{\var(X)} \cov(X, Y) = \frac{\cov^2(X, Y)}{\var(X)} \]
Ahora podemos probar el resultado fundamental que\( L(Y \mid X) \) es la función lineal de la\( X \) que está más cerca\( Y \) en el sentido cuadrático medio. Damos dos pruebas; la primera es más directa, pero la segunda es más interesante y elegante.
Supongamos que\( U \) es una función lineal de\( X \). Entonces
- \( \E\left(\left[Y - L(Y \mid X)\right]^2\right) \le \E\left[(Y - U)^2\right] \)
- La igualdad ocurre en (a) si y sólo si\( U = L(Y \mid X) \) con probabilidad 1.
Prueba de cálculo
Dejar\(\mse(a, b)\) denotar el error cuadrático medio cuando\(U = a + b \, X\) se utiliza como estimador de\(Y\), en función de los parámetros\(a, \, b \in \R\):\[ \mse(a, b) = \E\left(\left[Y - (a + b \, X)\right]^2 \right) \] Expandiendo el cuadrado y usando la linealidad del valor esperado da\[ \mse(a, b) = a^2 + b^2 \E(X^2) + 2 a b \E(X) - 2 a \E(Y) - 2 b \E(X Y) + \E(Y^2) \] En términos de las variables\( a \) y\( b \), los tres primeros términos son los términos de segundo orden, los dos siguientes son los términos de primer orden y el último es el término de orden cero. Los términos de segundo orden definen una forma cuadrática cuya matriz simétrica estándar es\[ \left[\begin{matrix} 1 & \E(X) \\ \E(X) & \E(X^2) \end{matrix} \right]\] El determinante de esta matriz es\( \E(X^2) - [\E(X)]^2 = \var(X) \) y los términos diagonales son positivos. Todo esto significa que la gráfica de\( \mse \) es un paraboloide que se abre hacia arriba, por lo que el mínimo de\( \mse \) ocurrirá en el punto crítico único. Estableciendo las primeras derivadas de\( \mse \) a 0 tenemos\ begin {align} -2\ E (Y) + 2 b\ E (X) + 2 a & = 0\\ -2\ E (X Y) + 2 b\ E\ left (X^2\ right) + 2 a\ E (X) & = 0\ end {align} Resolviendo la primera ecuación para\( a \) da\( a = \E(Y) - b \E(X) \). Sustituir esto en la segunda ecuación y resolver da\( b = \cov(X, Y) \big/ \var(X) \).
Prueba usando propiedades
- Abreviamos\( L(Y \mid X) \)\( L \) por simplicidad. Supongamos que\( U \) es una función lineal de\( X \). Entonces\[ \E\left[(Y - U)^2\right] = \E\left(\left[(Y - L) + (L - U)\right]^2\right) = \E\left[(Y - L)^2\right] + 2 \E\left[(Y - L)(L - U)\right] + \E\left[(L - U)^2\right] \] Desde\( Y - L \) tiene media 0, el término medio es\( \cov(Y - L, L - U) \). Pero\( L \) y\( U \) son funciones lineales de\( X \) y por lo tanto así es\( L - U \). Así\( \cov(Y - L, L - U) = 0 \) por (23). De ahí\[ \E\left[(Y - U)^2\right] = \E\left[(Y - L)^2\right] + \E\left[(L - U)^2\right] \ge \E\left[(Y - L)^2\right] \]
- La igualdad ocurre en (a) si y sólo si\( \E\left[(L - U)^2\right] = 0 \), si y sólo si\( \P(L = U) = 1 \).
El error cuadrático medio cuando\( L(Y \mid X) \) se utiliza como predictor de\( Y \) es\[ \E\left(\left[Y - L(Y \mid X)\right]^2 \right) = \var(Y)\left[1 - \cor^2(X, Y)\right] \]
Prueba
Nuevamente, vamos\( L = L(Y \mid X) \) por conveniencia. Ya que\( Y - L \) tiene media 0,\[ \E\left[(Y - L)^2\right] = \var(Y - L) = \var(Y) - 2 \cov(L, Y) + \var(L) \] Pero\( \cov(L, Y) = \var(L) = \cov^2(X, Y) \big/ \var(X) \) por (24). De ahí\[ \E\left[(Y - L)^2\right] = \var(Y) - \frac{\cov^2(X, Y)}{\var(X)} = \var(Y) \left[1 - \frac{\cov^2(X, Y)}{\var(X) \var(Y)}\right] = \var(Y) \left[1 - \cor^2(X, Y)\right] \]
Nuestra solución a los mejores problemas de perdictores lineales produce importantes propiedades de covarianza y correlación.
Propiedades adicionales de covarianza y correlación:
- \(-1 \le \cor(X, Y) \le 1\)
- \(-\sd(X) \sd(Y) \le \cov(X, Y) \le \sd(X) \sd(Y)\)
- \(\cor(X, Y) = 1\)si y sólo si, con probabilidad 1,\(Y\) es una función lineal de\( X \) con pendiente positiva.
- \(\cor(X, Y) = - 1\)si y sólo si, con probabilidad 1,\(Y\) es una función lineal de\( X \) con pendiente negativa.
Prueba
Dado que el error cuadrático medio no es negativo, se deduce de (26) que\(\cor^2(X, Y) \le 1\). Esto da las partes (a) y (b). Para las partes (c) y (d), tenga en cuenta que si\(\cor^2(X, Y) = 1\) entonces\(Y = L(Y \mid X)\) con probabilidad 1, y que la pendiente en\( L(Y \mid X) \) tiene el mismo signo que\( \cor(X, Y) \).
Los dos últimos resultados muestran claramente eso\(\cov(X, Y)\) y\(\cor(X, Y)\) miden la asociación lineal entre\(X\) y\(Y\). Las desigualdades equivalentes (a) y (b) anteriores son referidas como la desigualdad de correlación. También son versiones de la desigualdad Cauchy-Schwarz, llamada así por Augustin Cauchy y Karl Schwarz
Recordemos de nuestra discusión previa de varianza que el mejor predictor constante de\(Y\), en el sentido de minimizar el error cuadrático medio, es\(\E(Y)\) y el valor mínimo del error cuadrático medio para este predictor es\(\var(Y)\). Así, la diferencia entre la varianza de\(Y\) y el error cuadrático medio anterior para\( L(Y \mid X) \) es la reducción en la varianza de\(Y\) cuando\(X\) se agrega el término lineal in al predictor:\[\var(Y) - \E\left(\left[Y - L(Y \mid X)\right]^2\right) = \var(Y) \, \cor^2(X, Y)\] Así\(\cor^2(X, Y)\) es la proporción de reducción en \(\var(Y)\)cuando\(X\) se incluye como variable predictora. Esta cantidad se denomina coeficiente de determinación (distribución). Ahora vamos
\[ L(Y \mid X = x) = \E(Y) + \frac{\cov(X, Y)}{\var(X)}\left[x - \E(X)\right], \quad x \in \R \]
La función\(x \mapsto L(Y \mid X = x)\) se conoce como la función de regresión de distribución para\(Y\) dado\(X\), y su gráfica se conoce como la línea de regresión de distribución. Tenga en cuenta que la línea de regresión pasa a través\(\left(\E(X), \E(Y)\right)\), el centro de la distribución conjunta.
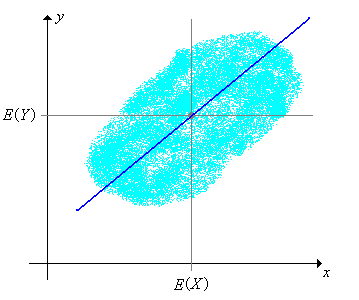
Sin embargo, la elección de la variable predictora y la variable de respuesta es crucial.
La línea de regresión para\(Y\) dado\(X\) y la línea de regresión para\(X\) dado no\(Y\) son la misma línea, excepto en el caso trivial donde las variables están perfectamente correlacionadas. Sin embargo, el coeficiente de determinación es el mismo, independientemente de qué variable es el predictor y cuál es la respuesta.
Prueba
Las dos líneas de regresión son\ begin {align} y -\ E (Y) & =\ frac {\ cov (X, Y)} {\ var (X)}\ left [x -\ E (X)\ right]\\ x -\ E (X) & =\ frac {\ cov (X, Y)} {\ var (Y)}\ left [y -\ E (Y)\ derecha]\ end {align} Las dos líneas son iguales si y solo si\( \cov^2(X, Y) = \var(X) \var(Y) \). Pero esto equivale a\( \cor^2(X, Y) = 1 \).
Supongamos que\(A\) y\(B\) son eventos con\(0 \lt \P(A) \lt 1\) y\(0 \lt \P(B) \lt 1\). Entonces
- \(\cor(A, B) = 1\)si y sólo\(\P(A \setminus B) + \P(B \setminus A) = 0\). (Es decir,\(A\) y\(B\) son eventos equivalentes.)
- \(\cor(A, B) = - 1\)si y sólo\(\P(A \setminus B^c) + \P(B^c \setminus A) = 0\). (Es decir,\(A\) y\(B^c\) son eventos equivalentes.)
Prueba
Recordemos de (19) eso\(\cor(A, B) = \cor(\bs 1_A, \bs 1_B)\), así que si\(\cor^2(A, B) = 1\) entonces de (27),\(\bs 1_B = L(\bs 1_B \mid \bs 1_A)\) con probabilidad 1. Pero\(\bs 1_A\) y\(\bs 1_B\) cada uno toma valores 0 y 1 solamente. De ahí que las únicas líneas de regresión posibles son\(y = 0\)\(y = 1\),,\(y = x\) y\(y = 1 - x\). Los dos primeros corresponden a\(\P(B) = 0\) y\(\P(B) = 1\), respectivamente, los cuales están excluidos por las hipótesis.
- En este caso, la pendiente es positiva, por lo que la línea de regresión lo es\(y = x\). Es decir,\(\bs 1_B = \bs 1_A\) con probabilidad 1.
- En este caso, la pendiente es negativa, por lo que la línea de regresión lo es\(y = 1 - x\). Es decir,\(\bs 1_B = 1 - \bs 1_A = \bs 1_{A^c}\) con probabilidad 1.
El concepto de mejor predictor lineal es más potente de lo que podría aparecer primero, ya que se puede aplicar a las transformaciones de las variables. Específicamente, supongamos que\(X\) y\(Y\) son variables aleatorias para nuestro experimento, tomando valores en espacios generales\(S\) y\(T\), respectivamente. Supongamos también que\(g\) y\(h\) son funciones de valor real definidas en\(S\) y\(T\), respectivamente. Podemos encontrar\(L\left[h(Y) \mid g(X)\right]\), la función lineal de\(g(X)\) eso es más cercana\(h(Y)\) en el sentido cuadrático medio. Los resultados de esta subsección aplican, por supuesto, con el\(g(X)\) reemplazo\(X\) y el\(h(Y)\) reemplazo\(Y\). Por supuesto, debemos ser capaces de computar los medios, varianzas y covarianzas apropiados.
Cerramos esta subsección con dos propiedades adicionales del mejor predictor lineal, las propiedades de linealidad.
Supongamos que\( X \)\( Y \),, y\(Z\) son variables aleatorias y que\(c\) es una constante. Entonces
- \(L(Y + Z \mid X) = L(Y \mid X) + L(Z \mid X)\)
- \(L(c Y \mid X) = c L(Y \mid X)\)
Prueba de las definiciones
Estos resultados se derivan fácilmente de la linealidad del valor esperado y la covarianza.
- \ begin {align} L (Y + Z\ mid X) & =\ E (Y + Z) +\ frac {\ cov (X, Y + Z)} {\ var (X)}\ izquierda [X -\ E (X)\ derecha]\\ &=\ izquierda (\ E (Y) +\ frac {\ cov (X, Y)} {\ var (X)} izquierda\ [X -\ E (X)\ derecha]\ derecha) +\ izquierda (\ E (Z) +\ frac {\ cov (X, Z)} {\ var (X)}\ izquierda [X -\ E (X)\ derecha]\ derecha)\\ & =\ E (Y\ media X) +\ E (Z\ media X)\ final {alinear}
- \[ L(c Y \mid X) = \E(c Y) + \frac{\cov(X, cY)}{\var(X)}\left[X - \E(X)\right] = c \E(Y) + c \frac{\cov(X, Y)}{\var(X)}\left[X - \E(X)\right] = c L(Y \mid X) \]
Prueba caracterizando propiedades
- Mostramos que\( L(Y \mid X) + L(Z \mid X) \) satisfacen las propiedades que caracterizan\( L(Y + Z \mid X) \). \ begin {align}\ E\ left [L (Y\ mid X) + L (Z\ mid X)\ right] & =\ E\ left [L (Y\ mid X)\ right] +\ E\ left [L (Z\ mid X)\ right] =\ E (Y) +\ E (Z) =\ E (Y + Z)\\ cov\ left [X, Y (\ media X) + L (Z\ media X)\ derecha] & =\ cov\ izquierda [X, L (Y\ media X)\ derecha] +\ cov\ izquierda [X, L (Z\ media X)\ derecha] =\ cov (X, Y) +\ cov (X, Z) =\ cov (X, Y + Z)\ fin {align}
- De igual manera, mostramos que\( c L(Y \mid X) \) satisface las propiedades que caracterizan\( L(c Y \mid X) \)\ begin {align}\ E\ left [c L (Y\ mid X)\ right] & = c\ E\ left [L (Y\ mid X)\ right] = c\ E (Y) =\ E (c Y)\\ cov\ left [X, c L (Y\ mid X)\ right] & = c\,\ cov\ izquierda [X, L (Y\ media X)\ derecha] = c\,\ cov (X, Y) =\ cov (X, c Y)\ end { alinear}
Existen varias ampliaciones y generalizaciones de las ideas en la subsección:
- El problema estadístico correspondiente de estimación\(a\) y\(b\), cuando se desconocen estos parámetros de distribución, se considera en la sección sobre Covarianza y Correlación de la Muestra.
- El problema de encontrar la función de\(X\) eso es más cercana\(Y\) en el sentido del error cuadrático medio (usando todas las funciones razonables, no solo funciones lineales) se considera en la sección de Valor esperado condicional.
- El mejor problema de predicción lineal cuando las variables predictoras y de respuesta son vectores aleatorios se considera en la sección Matrices de Valor Esperado y Covarianza.
El uso de propiedades caracterizantes jugará un papel crucial en estas extensiones.
Ejemplos y Aplicaciones
Distribuciones Uniformes
Supongamos que\(X\) se distribuye uniformemente en el intervalo\([-1, 1]\) y\(Y = X^2\). Entonces\(X\) y no\(Y\) están correlacionados aunque\(Y\) sea una función de\(X\) (la forma más fuerte de dependencia).
Prueba
Tenga en cuenta que\( \E(X) = 0 \) y\( \E(Y) = \E\left(X^2\right) = 1 / 3 \) y\( \E(X Y) = E\left(X^3\right) = 0 \). De ahí\( \cov(X, Y) = \E(X Y) - \E(X) \E(Y) = 0 \).
Supongamos que\((X, Y)\) se distribuye uniformemente en la región\(S \subseteq \R^2\). Encuentre\(\cov(X, Y)\)\(\cor(X, Y)\) y determine si las variables son independientes en cada uno de los siguientes casos:
- \(S = [a, b] \times [c, d]\)donde\(a \lt b\) y\(c \lt d\), así\( S \) es un rectángulo.
- \(S = \left\{(x, y) \in \R^2: -a \le y \le x \le a\right\}\)donde\(a \gt 0\), así\( S \) es un triángulo
- \(S = \left\{(x, y) \in \R^2: x^2 + y^2 \le r^2\right\}\)donde\(r \gt 0\), así\( S \) es un círculo
Contestar
- \( \cov(X, Y) = 0\),\(\cor(X, Y) = 0\). \( X \)y\( Y \) son independientes.
- \(\cov(X, Y) = \frac{a^2}{9}\),\(\cor(X, Y) = \frac{1}{2}\). \( X \)y\( Y \) son dependientes.
- \(\cov(X, Y) = 0\),\(\cor(X, Y) = 0\). \( X \)y\( Y \) son dependientes.
En el experimento uniforme bivariado, seleccione cada una de las regiones siguientes a su vez. Para cada región, ejecute la simulación 2000 veces y anote el valor de la correlación y la forma de la nube de puntos en la gráfica de dispersión. Comparar con los resultados del último ejercicio.
- Cuadrado
- Triángulo
- Círculo
Supongamos que\(X\) se distribuye uniformemente en el intervalo\((0, 1)\) y que dado\(X = x \in (0, 1)\),\(Y\) se distribuye uniformemente en el intervalo\((0, x)\). Encuentra cada uno de los siguientes:
- \(\cov(X, Y)\)
- \(\cor(X, Y)\)
- \(L(Y \mid X)\)
- \(L(X \mid Y)\)
Contestar
- \(\frac{1}{24}\)
- \(\sqrt{\frac{3}{7}}\)
- \(\frac{1}{2} X\)
- \(\frac{2}{7} + \frac{6}{7} Y\)
Dados
Recordemos que un dado estándar es un dado de seis lados. Un dado justo es aquel en el que las caras son igualmente probables. Un troquel plano ace-seis es un dado estándar en el que las caras 1 y 6 tienen probabilidad\(\frac{1}{4}\) cada una, y las caras 2, 3, 4 y 5 tienen probabilidad\(\frac{1}{8}\) cada una.
Se lanzan un par de dados estándar y justos y se\((X_1, X_2)\) registran los puntajes. Dejar\(Y = X_1 + X_2\) denotar la suma de las puntuaciones,\(U = \min\{X_1, X_2\}\) las puntuaciones mínimas y\(V = \max\{X_1, X_2\}\) la puntuación máxima. Encuentra la covarianza y correlación de cada uno de los siguientes pares de variables:
- \((X_1, X_2)\)
- \((X_1, Y)\)
- \((X_1, U)\)
- \((U, V)\)
- \((U, Y)\)
Contestar
- \(0\),\(0\)
- \(\frac{35}{12}\),\(\frac{1}{\sqrt{2}} = 0.7071\)
- \(\frac{35}{24}\),\(0.6082\)
- \(\frac{1369}{1296}\),\(\frac{1369}{2555} = 0.5358\)
- \(\frac{35}{12}\),\(0.8601\)
Supongamos que se tiran dados\(n\) justos. Encuentra la media y varianza de cada una de las siguientes variables:
- \( Y_n \), la suma de los puntajes.
- \( M_n \), el promedio de los puntajes.
Contestar
- \(\E\left(Y_n\right) = \frac{7}{2} n\),\(\var\left(Y_n\right) = \frac{35}{12} n\)
- \(\E\left(M_n\right) = \frac{7}{2}\),\(\var\left(M_n\right) = \frac{35}{12 n}\)
En el experimento de dados, seleccione dados justos y seleccione las siguientes variables aleatorias. En cada caso, aumentar el número de dados y observar el tamaño y ubicación de la función de densidad de probabilidad y la barra de desviación\( \pm \) estándar media. Con\(n = 20\) dados, ejecute el experimento 1000 veces y compare la media de la muestra y la desviación estándar con la media de distribución y la desviación estándar.
- La suma de los puntajes.
- El promedio de los puntajes.
Supongamos\(n\) que se lanzan dados planos ase-seis. Encuentra la media y varianza de cada una de las siguientes variables:
- \( Y_n \), la suma de los puntajes.
- \( M_n \), el promedio de los puntajes.
Contestar
- \(n \frac{7}{2}\),\(n \frac{15}{4}\)
- \(\frac{7}{2}\),\(\frac{15}{4 n}\)
En el experimento de dados, seleccione los dados planos ace-seis y seleccione las siguientes variables aleatorias. En cada caso, aumentar el número de dados y observar el tamaño y ubicación de la función de densidad de probabilidad y la barra de desviación\( \pm \) estándar media. Con\(n = 20\) dados, ejecute el experimento 1000 veces y compare la media de la muestra y la desviación estándar con la media de distribución y la desviación estándar.
- La suma de los puntajes.
- El promedio de los puntajes.
Se lanzan un par de dados justos y se\((X_1, X_2)\) registran los puntajes. Dejar\(Y = X_1 + X_2\) denotar la suma de las puntuaciones,\(U = \min\{X_1, X_2\}\) la puntuación mínima y\(V = \max\{X_1, X_2\}\) la puntuación máxima. Encuentra cada uno de los siguientes:
- \(L(Y \mid X_1)\)
- \(L(U \mid X_1)\)
- \(L(V \mid X_1)\)
Contestar
- \(\frac{7}{2} + X_1\)
- \(\frac{7}{9} + \frac{1}{2} X_1\)
- \(\frac{49}{19} + \frac{1}{2} X_1\)
Juicios de Bernoulli
Recordemos que un proceso de ensayos de Bernoulli es una secuencia\(\boldsymbol{X} = (X_1, X_2, \ldots)\) de variables aleatorias indicadoras independientes, distribuidas idénticamente. En el lenguaje habitual de confiabilidad,\(X_i\) denota el resultado del ensayo\(i\), donde 1 denota éxito y 0 denota fracaso. La probabilidad de éxito\(p = \P(X_i = 1)\) es el parámetro básico del proceso. El proceso lleva el nombre de Jacob Bernoulli. Un capítulo separado sobre los juicios de Bernoulli explora este proceso en detalle.
Porque\(n \in \N_+\), el número de éxitos en los primeros\(n\) ensayos es\(Y_n = \sum_{i=1}^n X_i\). Recordemos que esta variable aleatoria tiene la distribución binomial con parámetros\(n\) y\(p\), que tiene la función de densidad de probabilidad\(f\) dada por
\[ f_n(y) = \binom{n}{y} p^y (1 - p)^{n - y}, \quad y \in \{0, 1, \ldots, n\} \]
La media y varianza de\(Y_n\) son
- \(\E(Y_n) = n p\)
- \(\var(Y_n) = n p (1 - p)\)
Prueba
Estos resultados podrían derivarse del PDF de\( Y_n \), por supuesto, pero una derivación basada en la suma de variables IID es mucho mejor. Recordemos eso\( \E(X_i) = p \) y\( \var(X_i) = p (1 - p) \) así los resultados siguen inmediatamente del teorema (16).
En el experimento de monedas binomiales, seleccione el número de cabezas. Varíe\(n\)\(p\) y anote la forma de la función de densidad de probabilidad y el tamaño y ubicación de la barra de desviación\( \pm \) estándar media. Para valores seleccionados de los parámetros, ejecute el experimento 1000 veces y compare la media de la muestra y la desviación estándar con la media de distribución y la desviación estándar.
Pues\(n \in \N_+\), la proporción de éxitos en los primeros\(n\) ensayos es\(M_n = Y_n / n\). Esta variable aleatoria se utiliza a veces como estimador estadístico del parámetro\(p\), cuando el parámetro es desconocido.
La media y varianza de\(M_n\) son
- \(\E(M_n) = p\)
- \(\var(M_n) = p (1 - p) / n\)
Prueba
Recordemos eso\( \E(X_i) = p \) y\( \var(X_i) = p (1 - p) \) así los resultados siguen inmediatamente del teorema (17).
En el experimento de monedas binomiales, seleccione la proporción de cabezas. Varíe\(n\)\(p\) y anote la forma de la función de densidad de probabilidad y el tamaño y ubicación de la barra de desviación\( \pm \) estándar media. Para valores seleccionados de los parámetros, ejecute el experimento 1000 veces y compare la media de la muestra y la desviación estándar con la media de distribución y la desviación estándar.
Como caso especial de (17) señalar que\(M_n \to p\) como\(n \to \infty\) en el cuadrado medio y en probabilidad.
La distribución hipergeométrica
Supongamos que una población consiste en\(m\) objetos;\(r\) de los objetos son tipo 1 y\(m - r\) son tipo 0. Se elige una muestra de\(n\) objetos al azar, sin reemplazo. Los parámetros\(m, \, n \in \N_+\) y\(r \in \N\) con\(n \le m\) y\(r \le m\). For\(i \in \{1, 2, \ldots, n\}\), let\(X_i\) denotar el tipo del objeto\(i\) th seleccionado. Recordemos que\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias indicadoras distribuidas idénticamente (pero no independientes).
Dejar\(Y\) denotar el número de objetos tipo 1 en la muestra, de modo que eso\(Y = \sum_{i=1}^n X_i\). Recordemos que esta variable aleatoria tiene la distribución hipergeométrica, que tiene la función de densidad de probabilidad\(f_n\) dada por
\[ f(y) = \frac{\binom{r}{y} \binom{m - r}{n - y}}{\binom{m}{n}}, \quad y \in \{0, 1, \ldots, n\} \]
Para distintos\(i, \, j \in \{1, 2, \ldots, n\}\),
- \( \E(X_i) = \frac{r}{m} \)
- \( \var(X_i) = \frac{r}{m} \left(1 - \frac{r}{m}\right) \)
- \(\cov(X_i, X_j) = -\frac{r}{m}\left(1 - \frac{r}{m}\right) \frac{1}{m - 1}\)
- \(\cor(X_i, X_j) = -\frac{1}{m - 1}\)
Prueba
Recordemos eso\( \E(X_i) = \P(X_i = 1) = \frac{r}{m} \) para cada uno\( i \) y\( \E(X_i X_j) = \P(X_i = 1, X_j = 1) = \frac{r}{m} \frac{r - 1}{m - 1} \) para cada uno\( i \ne j \). Técnicamente, la secuencia de variables indicadoras es intercambiable. Los resultados se derivan ahora de las definiciones y álgebra simple.
Tenga en cuenta que el evento de un objeto tipo 1 al dibujar\(i\) y el evento de un objeto tipo 1 en el dibujo\(j\) están correlacionados negativamente, pero la correlación depende únicamente del tamaño de la población y no del número de objetos de tipo 1. Tenga en cuenta también que la correlación es perfecta si\(m = 2\). Piense en estos resultados de manera intuitiva.
La media y varianza de\(Y\) son
- \(\E(Y) = n \frac{r}{m}\)
- \(\var(Y) = n \frac{r}{m}\left(1 - \frac{r}{m}\right) \frac{m - n}{m - 1}\)
Obsérvese que si el muestreo fuera con reemplazo,\( Y \) tendría una distribución binomial, y así en particular\( E(Y) = n \frac{r}{m} \) y\( \var(Y) = n \frac{r}{m} \left(1 - \frac{r}{m}\right) \). El factor adicional\( \frac{m - n}{m - 1} \) que ocurre en la varianza de la distribución hipergeométrica a veces se denomina factor de corrección poblacional finita. Tenga en cuenta que para fijo\( m \),\( \frac{m - n}{m - 1} \) está disminuyendo en\( n \), y es 0 cuando\( n = m \). Por supuesto, sabemos que debemos tener\( \var(Y) = 0 \) si\( n = m \), ya que estaríamos muestreando a toda la población, y así determinísticamente,\( Y = r \). Por otro lado, para fijo\( n \),\( \frac{m - n}{m - 1} \to 1\) como\( m \to \infty \). De manera más general, la distribución hipergeométrica es bien aproximada por el binomio cuando el tamaño de la población\( m \) es grande en comparación con el tamaño de la muestra\( n \). Estas ideas se discuten más a fondo en la sección sobre la distribución hipergeométrica en el capítulo sobre Modelos de Muestreo Finito.
En el experimento de bola y urna, seleccione muestreo sin reemplazo. Varíe\(m\)\(r\),\(n\) y anote la forma de la función de densidad de probabilidad y el tamaño y ubicación de la barra de desviación\( \pm \) estándar media. Para valores seleccionados de los parámetros, ejecute el experimento 1000 veces y compare la media de la muestra y la desviación estándar con la media de distribución y la desviación estándar.
Ejercicios sobre Propiedades Básicas
Supongamos que\(X\) y\(Y\) son variables aleatorias de valor real con\(\cov(X, Y) = 3\). Encuentra\(\cov(2 X - 5, 4 Y + 2)\).
Contestar
24
Supongamos\(X\) y\(Y\) son variables aleatorias de valor real con\(\var(X) = 5\)\(\var(Y) = 9\),, y\(\cov(X, Y) = - 3\). Encuentra
- \( \cor(X, Y) \)
- \(\var(2 X + 3 Y - 7)\)
- \(\cov(5 X + 2 Y - 3, 3 X - 4 Y + 2)\)
- \(\cor(5 X + 2 Y - 3, 3 X - 4 Y + 2)\)
Contestar
- \( -\frac{1}{\sqrt{5}} \approx -0.4472 \)
- 65
- 45
- \( \frac{15}{\sqrt{2929}} \approx 0.2772\)
Supongamos que\(X\) y\(Y\) son variables aleatorias independientes, de valor real con\(\var(X) = 6\) y\(\var(Y) = 8\). Encuentra\(\var(3 X - 4 Y + 5)\).
Contestar
182
Supongamos que\(A\) y\(B\) son eventos en un experimento con\(\P(A) = \frac{1}{2}\),\(\P(B) = \frac{1}{3}\), y\(\P(A \cap B) = \frac{1}{8}\). Encuentra cada uno de los siguientes:
- \( \cov(A, B) \)
- \( \cor(A, B) \)
Contestar
- \(-\frac{1}{24}\)
- \(-\sqrt 2 / 8 \)
Supongamos que\( X \)\( Y \),, y\( Z \) son variables aleatorias de valor real para un experimento, y eso\( L(Y \mid X) = 2 - 3 X \) y\( L(Z \mid X) = 5 + 4 X \). Encuentra\( L(6 Y - 2 Z \mid X) \).
Contestar
\( 2 - 26 X \)
Supongamos que\( X \) y\( Y \) son variables aleatorias de valor real para un experimento, y eso\( \E(X) = 3 \),\( \var(X) = 4 \), y\( L(Y \mid X) = 5 - 2 X \). Encuentra cada uno de los siguientes:
- \( \E(Y) \)
- \( \cov(X, Y) \)
Contestar
- \( -1 \)
- \( -8 \)
Distribuciones Continuas Simples
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = x + y\) for\(0 \le x \le 1\),\(0 \le y \le 1\). Encuentra cada uno de los siguientes
- \(\cov(X, Y)\)
- \(\cor(X, Y)\)
- \(L(Y \mid X)\)
- \(L(X \mid Y)\)
Contestar
- \(-\frac{1}{144}\)
- \(-\frac{1}{11} \approx -0.0909\)
- \(\frac{7}{11} - \frac{1}{11} X\)
- \(\frac{7}{11} = \frac{1}{11} Y\)
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 2 (x + y)\) for\(0 \le x \le y \le 1\). Encuentra cada uno de los siguientes:
- \(\cov(X, Y)\)
- \(\cor(X, Y)\)
- \(L(Y \mid X)\)
- \(L(X \mid Y)\)
Contestar
- \(\frac{1}{48}\)
- \(\frac{5}{\sqrt{129}} \approx 0.4402\)
- \(\frac{26}{43} + \frac{15}{43} X\)
- \(\frac{5}{9} Y\)
Supongamos nuevamente que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) dada por\(f(x, y) = 2 (x + y)\) for\(0 \le x \le y \le 1\).
- Encuentra\(\cov\left(X^2, Y\right)\).
- Encuentra\(\cor\left(X^2, Y\right)\).
- Encuentra\(L\left(Y \mid X^2\right)\).
- ¿Cuál predictor de\(Y\) es mejor, el basado\(X\) o el basado en\(X^2\)?
Contestar
- \(\frac{7}{360}\)
- \(0.448\)
- \(\frac{1255}{1920} + \frac{245}{634} X\)
- El predictor basado en\(X^2\) es ligeramente mejor.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 6 x^2 y\) for\(0 \le x \le 1\),\(0 \le y \le 1\). Encuentra cada uno de los siguientes:
- \(\cov(X, Y)\)
- \(\cor(X, Y)\)
- \(L(Y \mid X)\)
- \(L(X \mid Y)\)
Contestar
Tenga en cuenta que\(X\) y\(Y\) son independientes.
- \(0\)
- \(0\)
- \(\frac{2}{3}\)
- \(\frac{3}{4}\)
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 15 x^2 y\) for\(0 \le x \le y \le 1\). Encuentra cada uno de los siguientes:
- \(\cov(X, Y)\)
- \(\cor(X, Y)\)
- \(L(Y \mid X)\)
- \(L(X \mid Y)\)
Contestar
- \(\frac{5}{336}\)
- \(0.05423\)
- \(\frac{30}{51} + \frac{20}{51} X\)
- \(\frac{3}{4} Y\)
Supongamos nuevamente que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) dada por\(f(x, y) = 15 x^2 y\) for\(0 \le x \le y \le 1\).
- Encuentra\(\cov\left(\sqrt{X}, Y\right)\).
- Encuentra\(\cor\left(\sqrt{X}, Y\right)\).
- Encuentra\(L\left(Y \mid \sqrt{X}\right)\).
- ¿Cuál de los predictores de\(Y\) es mejor, el basado en\(X\) el basado en el basado\(\sqrt{X}\)?
Contestar
- \(\frac{10}{1001}\)
- \(\frac{24}{169} \sqrt{14}\)
- \(\frac{5225}{13\;182} + \frac{1232}{2197} X\)
- El predictor basado en\(X\) es ligeramente mejor.


