16.5: Periodicidad de las Cadenas Discretas de Tiempo
- Page ID
- 151956
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un estado en una cadena de Markov de tiempo discreto es periódico si la cadena puede regresar al estado solo en múltiplos de algún número entero mayor que 1. El comportamiento periódico complica el estudio del comportamiento limitante de la cadena. Como veremos en esta sección, podemos eliminar el comportamiento periódico considerando la cadena\( d \) -step, donde\( d \in \N_+ \) está el periodo, pero sólo a costa de introducir clases de equivalencia adicionales. Así, en cierto sentido, podemos intercambiar una forma de complejidad por otra.
Teoría Básica
Definiciones y Resultados Básicos
Como es habitual, nuestro punto de partida es una cadena de Markov discreto-tiempo (homogénea en el tiempo)\( \bs{X} = (X_0, X_1, X_2, \ldots) \) con espacio de estado (contable)\( S \) y matriz de probabilidad de transición\( P \).
El periodo de estado\( x \in S \) es\[ d(x) = \gcd\{n \in \N_+: P^n(x, x) \gt 0 \} \] Estado\( x \) es aperiódico si\( d(x) = 1 \) y periódico si\( d(x) \gt 1 \).
Así, a partir de\( x \), la cadena puede volver a\( x \) solo en múltiplos del periodo\( d \), y\( d \) es el mayor número entero de este tipo. Quizás el resultado más importante es que el período, como la recurrencia y la fugacidad, es una propiedad de clase, compartida por todos los estados en una clase de equivalencia bajo la relación de ida y vuelta.
Si\( x \leftrightarrow y \) entonces\( d(x) = d(y) \).
Prueba
Supongamos que\( x \leftrightarrow y \). El resultado es trivial si\( x = y \), así que supongamos que\( x \neq y \). Recordemos que existen\( j, \, k \in \N_+ \) tal que\( P^j(x, y) \gt 0 \) y\( P^k(y, x) \gt 0 \). Pero entonces\( P^{j+k}(x, x) \ge P^j(x, y) P^k(y, x) \gt 0 \) y por lo tanto\( d(x) \mid (j + k) \). Supongamos ahora que\( n \) es un entero positivo con\( P^n(y, y) \gt 0 \). Entonces\( P^{j+k+n}(x, x) \ge P^j(x, y) P^n(y, y) P^k(y, x) \gt 0 \) y por lo tanto\( d(x) \mid (j + k + n) \). De ello se deduce que\( d(x) \mid n \). A partir de la definición de periodo,\( d(y) \mid d(x) \). Revertir los roles de\( x \) y también\( y \) tenemos\( d(x) \mid d(y) \). De ahí\( d(x) = d(y) \).
Así, las definiciones de periodo, periódica y aperiódica se aplican tanto a las clases de equivalencia como a los estados individuales. Cuando la cadena es irreducible, podemos aplicar estos términos a toda la cadena.
Supongamos que\( x \in S \). Si\( P(x, x) \gt 0 \) entonces\( x \) (y por lo tanto la clase de equivalencia de\( x \)) es aperiódica.
Prueba
Por suposición,\( 1 \in \{n \in \N_+: P^n(x, x) \gt 0\} \) y de ahí el mayor divisor común de este conjunto es 1.
Lo contrario no es cierto, claro. A continuación se da un simple contraejemplo.
Las clases cíclicas
Supongamos ahora que\( \bs{X} = (X_0, X_1, X_2, \ldots) \) es irreducible y es periódico con periodo\( d \). No hay pérdida real en generalidad al asumir que la cadena es irreducible, pues si no fuera así, simplemente podríamos restringir nuestra atención a una de las clases de equivalencia irreducible. Nuestra exposición será más fácil y limpia si recordamos la relación de equivalencia congruencia módulo\( d \) on\( \Z \), que a su vez se basa en el orden parcial divison. Para\( n, \, m \in \Z \),\( n \equiv_d m \) si y solo si\( d \mid (n - m) \), equivalentemente\( n - m \) es un entero múltiplo de\( d \), equivalentemente\( m \) y\( n \) tener el mismo resto después de la división por\( d \). El hecho básico que necesitaremos es que\( \equiv_d \) se conserve bajo sumas y diferencias. Es decir, si\( m, \, n, \, p, \, q \in \Z \) y si\( m \equiv_d n \) y\( p \equiv_d q \), entonces\( m + p \equiv_d n + q \) y\( m - p \equiv_d n - q \).
Ahora, fijamos un estado de referencia\( u \in S \), y para\( k \in \{0, 1, \ldots, d - 1\} \), definimos Es\[ A_k = \{x \in S: P^{n d + k}(u, x) \gt 0 \text{ for some } n \in \N\} \] decir,\( x \in A_k \) si y sólo si existe\( m \in \N \) con\( m \equiv_d k \) y\( P^m(u, x) \gt 0 \).
Supongamos que\( x, \, y \in S \).
- Si\( x \in A_j \) y\( y \in A_k \) para\( j, \, k \in \{0, 1, \ldots, d - 1\} \) entonces\( P^n(x, y) \gt 0 \) para algunos\( n \equiv_d k - j \)
- Por el contrario, si\( P^n(x, y) \gt 0 \) para algunos\( n \in \N \), entonces existe\( j, \, k \in \{0, 1, \ldots d - 1\} \) tal que\( x \in A_j \),\( y \in A_k \) y\( n \equiv_d k - j \).
- La\( (A_0, A_1, \ldots, A_{k-1}) \) partición de conjuntos\( S \).
Prueba
Supongamos primero eso\( x \in A_k \). Por definición,\( u \) lleva\( x \) a\( m \) pasos para algunos\( m \equiv_d k \). Dado que la cadena es irreducible,\( x \) lleva de nuevo a\( u \), digamos en\( p \) pasos. De ello se deduce que\( u \) lleva de nuevo a\( u \)\( m + p \) pasos. Pero porque\( u \) tiene periodo\( d \), debemos tener\( m + p \equiv_d 0\) y por lo tanto\( p \equiv_d -k \).
Siguiente supongamos que\( x \in A_j \) y\( y \in A_k \). Sabemos que\( u \) lleva a\( x \)\( m \) pasos para algunos\( m \equiv_d j \), y ahora sabemos que\( y \) lleva a\( u \) en\( p \) pasos para algunos\( p \equiv_d -k \). Ya que la cadena es irreducible,\( x \) lleva a\( y \), digamos en\( n \) pasos. De ello se deduce que\( u \) lleva de nuevo a\( u \)\( m + n + p \) pasos. Nuevamente, ya que\( u \) tiene periodo\( d \),\( m + n + p \equiv_d 0 \) y se deduce que\( n \equiv_d k - j \)
A continuación, señalar que como la cadena es irreducible y ya que\(\{0, 1, \ldots, d - 1\}\) es el conjunto de todos los restos módulo\( d \), debemos tener\( \bigcup_{i=0}^{d-1} A_i = S \). Supongamos eso\( x, y \in S \) y\( P^n(x, y) \gt 0 \) para algunos\( n \in \N \). Entonces\( x \in A_j \) y\( y \in A_k \) para algunos\(j, \, k \in \{0, 1, \ldots\}\). Por el mismo argumento que el último párrafo, debemos tener\( n \equiv_d k - j \).
Todo lo que queda es demostrar que los conjuntos son disjuntos, y eso equivale una vez más al mismo viejo argumento. Supongamos que\( x \in A_j \cap A_k \) para algunos\( j, \, k \in \{0, 1, \ldots, d - 1\} \). Después\( u \) lleva a\( x \) en\( m \) pasos para algunos\( m \equiv_d j \) y\( x \) lleva a\( u \) en\( n \) pasos para algunos\( n \equiv_d - k \). De ahí\( u \) que nos lleve de nuevo a\( u \)\( m + n \) pasos. Como la cadena tiene periodo\( d \) tenemos\( m + n \equiv_d 0 \) y por lo tanto\( j - k \equiv_d 0 \). Ya que de\( j, \, k \in \{0, 1, \ldots, d - 1\} \) ello se deduce que\( j = k \).
\( (A_0, A_1, \ldots, A_{d-1}) \)son las clases de equivalencia para la relación\( d \) -paso hacia y desde\( \underset{d}{\leftrightarrow} \) que gobierna la cadena\( d \) -step\( (X_0, X_d, X_{2 d}, \ldots) \) que tiene matriz de transición\( P^d \).
Los conjuntos\( (A_0, A_1, \ldots, A_{d-1}) \) se conocen como las clases cíclicas. La estructura básica de la cadena se muestra en el diagrama de estados a continuación:
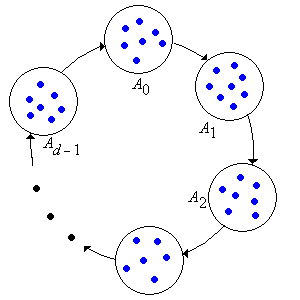
Ejemplos y Casos Especiales
Cadenas Finitas
Considere la cadena de Markov con espacio de estado\( S = \{a, b, c\} \) y matriz de transición\( P \) que se da a continuación:
\[ P = \left[\begin{matrix} 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}\right] \]- Esboza la gráfica estatal y muestra que la cadena es irreducible.
- Demostrar que la cadena es aperiódica.
- Tenga en cuenta que\( P(x, x) = 0 \) para todos\( x \in S \).
Responder
- La gráfica estatal tiene un conjunto de bordes\( E = \{(a, b), (a, c), (b, c), (b, a)\} \).
- Tenga en cuenta que\( P^2(a, a) \gt 0 \) y\( P^3(a, a) \gt 0 \). De ahí\( d(a) = 1 \) que ya que 2 y 3 son relativamente primos. Dado que la cadena es irreducible, es aperiódica.
Considere la cadena de Markov con espacio de estado\( S = \{1, 2, 3, 4, 5, 6, 7\} \) y matriz de transición\( P \) que se da a continuación:
\[ P = \left[\begin{matrix} 0 & 0 & \frac{1}{2} & \frac{1}{4} & \frac{1}{4} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 & \frac{2}{3} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & \frac{3}{4} & \frac{1}{4} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & 0 \\ \frac{1}{4} & \frac{3}{4} & 0 & 0 & 0 & 0 & 0 \end{matrix}\right] \]- Esboza la gráfica estatal y muestra que la cadena es irreducible.
- Encuentra el periodo\( d \).
- Encontrar\( P^d \).
- Identificar las clases cíclicas.
Responder
-
Gráfica estatal 
- Periodo 3
- \( P^3 = \left[ \begin{matrix} \frac{71}{192} & \frac{121}{192} & 0 & 0 & 0 & 0 & 0 \\ \frac{29}{72} & \frac{43}{72} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{7}{18} & \frac{1}{12} & \frac{19}{36} & 0 & 0 \\ 0 & 0 & \frac{19}{48} & \frac{3}{32} & \frac{49}{96} & 0 & 0 \\ 0 & 0 & \frac{13}{32} & \frac{7}{64} & \frac{31}{64} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{157}{299} & \frac{131}{288} \\ 0 & 0 & 0 & 0 & 0 & \frac{37}{64} & \frac{27}{64} \end{matrix} \right] \)
- Clases cíclicas:\( \{1, 2\} \),\( \{3, 4, 5\} \),\( \{6, 7\} \)
Modelos Especiales
Revisar la definición de la cadena básica de Ehrenfest. Demostrar que esta cadena tiene periodo 2, y encontrar las clases cíclicas.
Revisar la definición de la cadena Ehrenfest modificada. Demostrar que esta cadena es aperiódica.
Revisar la definición del simple paseo aleatorio\( \Z^k \). Mostrar que la cadena es periódica con el periodo 2, y encontrar las clases cíclicas.


