1.6: Soluciones armónicas de tiempo de la ecuación de onda

El hecho de que, en la circunstancia frecuente en la que la luz interactúa con un dieléctrico homogéneo, todos los componentes del campo electromagnético satisfacen la ecuación de onda escalar, justifica el estudio de soluciones de esta ecuación. Dado que en la mayoría de los casos en óptica se consideran campos monocromáticos, enfocaremos nuestra atención en soluciones armónicas de tiempo de la ecuación de onda.

1.5.1 Ondas planas armónicas de tiempo

Las soluciones armónicas de tiempo dependen del tiempo por un coseno o un seno. Uno puede verificar fácilmente por sustitución que

\[U(r,t)=Acos(kx-ωt+ϕ), \nonumber \]

donde A > 0 y 9 son constantes, es una solución de (1.4.10), siempre que

\[k = ω(Eµ_{0})^{1/2} = ωn(E_{0}µ_{0})^{1/2} = nk_{0}, \nonumber \]

donde k ₀ = ω (E ₀ µ ₀) ^1/2 es el número de onda en vacío. La frecuencia ω > 0 se puede elegir arbitrariamente. El número de onda k en el material se determina entonces por (\(\PageIndex{2}\)). Definimos T = 2π/ω y λ = 2π/k como el periodo y la longitud de onda en el material, respectivamente. Además, λ ₀ = 2π/k ₀ es la longitud de onda en vacío.

OBSERVACIÓN. Cuando hablamos de “la longitud de onda”, siempre nos referimos a la longitud de onda en vacío.

Podemos escribir (\(\PageIndex{1}\)) en el formulario

\[U(x,t)=Acos[k(x-\dfrac{c}{n}t)+ϕ], \nonumber \]

donde c/n = 1/ (Eµ ₀) ^1/2 es la velocidad de la luz en el material. A es la amplitud y el argumento bajo el coseno: k (x-ct/n) +φ se llama la fase en la posición x y en el tiempo t. Un frente de onda es un conjunto de puntos espacio-tiempo donde la fase es constante:

\[x-\dfrac{c}{n}t=constant. \nonumber \]

En cualquier momento fijo t los frentes de onda son planos (en este caso perpendiculares al eje x), y por lo tanto la onda se denomina onda plana. A medida que avanza el tiempo, los frentes de onda se mueven con la velocidad c/n en la dirección x positiva.

Una onda plana armónica de tiempo que se propaga en una dirección arbitraria viene dada por

\[U(r,t)=Acos(k · r-ωt+ϕ), \nonumber \]

donde A y φ son nuevamente constantes y k = k _{x x} + k _{y y} + k _{z z} es el vector de onda. Los frentes de onda vienen dados por el conjunto de todos los puntos de espacio-tiempo (r, t) para los cuales la fase k · r − ωt + φ es constante, es decir, para los cuales

\[k · r − ωt = constant. \nonumber \]

En tiempos fijos los frentes de onda son planos perpendiculares a la dirección de k como se muestra en la Fig. \(\PageIndex{1}\)Eq. (\(\PageIndex{5}\)) es una solución de (1.4.10) siempre que

\[k_{x}^2+k_{y}^2+k_{z}^2=ω^2Eµ_{0}=ω^2n^2E_{0}µ_{0}=k_{0}^2n^2. \nonumber \]

La dirección del vector de onda se puede elegir arbitrariamente, pero su longitud está determinada por la frecuencia ω.

1.5.2 Notación compleja para funciones armónicas de tiempo

Consideramos una solución armónica de tiempo general de la ecuación de onda (1.4.8):

\[U(r, t) = A(r) cos(ϕ(r) − ωt), \nonumber \]

donde la amplitud A (r) > 0 y la fase φ (r) son funciones de la posición r. Los frentes de onda consisten en puntos espacio-tiempo (r, t) donde la fase es constante:

\[ϕ(r) − ωt = constant. \nonumber \]

En el tiempo fijo t, los conjuntos de fase constante: φ (r) = ωt + constante son superficies que en general no son planos, de ahí que la solución en general no sea una onda plana. Eq. (\(\PageIndex{9}\)) podría ser, por ejemplo, una onda con frentes de onda esféricos, como se analiza a continuación.

OBSERVACIÓN. Una onda plana se extiende infinitamente y transporta y transporta una cantidad infinita de energía electromagnética. Por lo tanto, un plano plano no puede existir en la realidad, pero sin embargo es una idealización habitual porque, como se demostrará en la Sección 7.1, cada solución tiempo-armónica de la ecuación de onda siempre puede expandirse en términos de ondas planas de la forma (\(\PageIndex{5}\)).

Para soluciones armónicas de tiempo a menudo es conveniente usar notación compleja. Definir la amplitud compleja mediante:

\[U(r) = A(r)e^{iϕ(r)} \nonumber \]

Figura\(\PageIndex{1}\): Planos de fase constante.

es decir, el módulo del número complejo U (r) es la amplitud A (r) y el argumento de U (r) es la fase φ (r) a t = 0. La parte dependiente del tiempo de la fase: −ωt se separa así de la parte dependiente del espacio de la fase. Entonces (\(\PageIndex{8}\)) se puede escribir como

\[U(r, t) = Re [ U(r)e^{−iωt}] . \nonumber \]

Por lo tanto, U (r, t) es la parte real de la compleja función armónica de tiempo

\[U(r)e^{−iωt} . \nonumber \]

OBSERVACIÓN. La amplitud compleja U (r) también se llama campo complejo. En el caso de campos vectoriales como E y H hablamos de campos vectoriales complejos, o simplemente campos complejos. Amplitudes complejas y campos complejos (vector) son solo funciones de la posición r; se omite el factor dependiente del tiempo exp (−iωt). Para obtener la cantidad real significativa física, la amplitud compleja o campo complejo primero tiene que multiplicarse por exp (−iωt) y luego se debe tomar la parte real.

A lo largo de este libro se utiliza la siguiente convención:

Las cantidades físicas de valor real (ya sean armónicas de tiempo o tengan una dependencia más general del tiempo) se denotan con una letra caligráfica, por ejemplo, U, ε _x o H _x. Los símbolos están en negrita cuando se trata de un vector, por ejemplo ε o H. La amplitud compleja de una función armónica de tiempo está vinculada a la cantidad física real por (\(\PageIndex{11}\)) y se escribe como una letra ordinaria como U y E.

Es más fácil calcular con amplitudes complejas (campos complejos) que con funciones trigonométricas (coseno y seno). Siempre y cuando todas las operaciones realizadas en las funciones sean lineales, las operaciones se pueden realizar en las cantidades complejas. Para obtener la cantidad física de valor real del resultado (es decir, el resultado físico significativo), multiplique la amplitud compleja finalmente obtenida por exp (−iωt) y tome la parte real. La razón por la que esto funciona es que tomar la parte real se desplaza con operaciones lineales, es decir, tomar primero la parte real para obtener la cantidad física de valor real y luego operar sobre esta cantidad física real da el mismo resultado que operar en el escalar complejo y tomar la parte real al final.

Al sustituir (\(\PageIndex{12}\)) en la ecuación de onda (1.4.10) obtenemos

\[\bigtriangledown^2U(r,t)-n^2E_{0}µ_{0}\dfrac{\partial^2{U(r,t)}}{\partial{t^2}}=Re[\bigtriangledown^2U(r)e^{−iωt}]-n^2E_{0}µ_{0}Re[U(r)\dfrac{\partial^2{e^{-iωt}}}{\partial^2}]=Re[\bigtriangledown^2U(r)+ω^2n^2E_{0}µ_{0}U(r)]e^{-iωt}. \nonumber \]

Dado que esto debe desaparecer para todos los tiempos t, se deduce que la expresión compleja entre los corchetes {.} debe desaparecer. Para ver esto, considere por ejemplo las dos instancias t = 0 y t = π/ (2ω. De ahí concluimos que la amplitud compleja satisface

\[\bigtriangledown^2U(r)+k_{0}^2n^2U(r)=0, Helmholtz\space Equation, \nonumber \]

donde k ₀ = ω (E ₀ µ ₀) ^1/2 es el número de onda en vacío.

OBSERVACIÓN. La cantidad compleja de la que se tiene que tomar la parte real es: U exp (−iωt). No es necesario arrastrar el factor dependiente del tiempo exp (−iωt) a lo largo de los cálculos: basta con calcular solo con la amplitud compleja U, luego multiplicar por exp (−iωt) y luego tomar la parte real. Sin embargo, cuando se va a tomar una derivada con respecto al tiempo: /t el campo complejo se multiplica mucho por −iω. Esto también se hace en las ecuaciones de Maxwell armónicos de tiempo en la Sección 1.6 a continuación.

1.5.3 Ondas esféricas de armónicos

Una onda esférica depende de la posición solo por la distancia a un punto fijo. Por simplicidad elegimos el origen de nuestro sistema de coordenadas en este punto. Buscamos así una solución de la forma U (r, t) con r = (x2 + y2 + z2) 1/2. Para funciones simétricas esféricas tenemos

\[\bigtriangledown^2U(r,t)=\dfrac{1}{r}\dfrac{\partial^2}{\partial{r^2}}[rU(r,t)] \nonumber \]

Es fácil ver que fuera del origen

\[U(r,t)=\dfrac{f(±r-ct/n)}{r}, \nonumber \]

satisface (1.47) para cualquier elección para la función f, donde, como antes, c = 1/ (E0µ0) 1/2 es la velocidad de la luz y n = (E/E0) 1/2. De particular interés son las ondas esféricas armónicas de tiempo:

\[U(r, t) = \dfrac{A}{r}cos[ k ( ±r − \dfrac{c}{n}t) + ϕ] = \dfrac{A}{r}cos(±kr − ωt + ϕ) \nonumber \]

donde A es una constante

\[k = nω/c. \nonumber \]

y ±kr − ωt + φ es la fase en r y en el tiempo t. Los frentes de onda son puntos espacio-tiempo (r, t) donde la fase es constante:

\[±kr − ωt = constant, \nonumber \]

que son esferas que se mueven con la velocidad de la luz en la dirección radial. Cuando se elige el signo +, la onda se propaga hacia afuera, es decir, lejos del origen. La onda es entonces irradiada por una fuente en el origen. En efecto, si el signo + se mantiene en (\(\PageIndex{17}\)), entonces si el tiempo t aumenta, (\(\PageIndex{19}\)) implica que una superficie de fase constante se mueve hacia afuera. Del mismo modo, si se mantiene el signo −, la onda se propaga hacia el origen que luego actúa como sumidero. La amplitud de la onda A/r es proporcional a la distancia inversa a la fuente de sumidero. Dado que el flujo local de energía es proporcional al cuadrado A ² /r ², el flujo total a través de la superficie de cualquier esfera con centro el origen es independiente del radio de la esfera. Dado que hay una fuente o un sumidero en el origen, (\(\PageIndex{17}\)) satisface (\(\PageIndex{15}\)) sólo fuera del origen. Hay una función δ-como densidad de fuente en el lado derecho:

\[Eμ_{0}\dfrac{\partial^2}{\partial{t^2}}U(r, t) − \bigtriangledown^2U(r, t) = 4πA δ(r), \nonumber \]

donde el lado derecho corresponde ya sea a una fuente o sumidero en el origen, dependiendo del signo elegido en la fase.

Figura\(\PageIndex{2}\): Frentes de onda esféricos con amplitud decreciente con la distancia.

Figura\(\PageIndex{3}\): Planos de fase constante en sección transversal. Para un observador a gran distancia de la fuente, la onda esférica se parece a una onda plana.

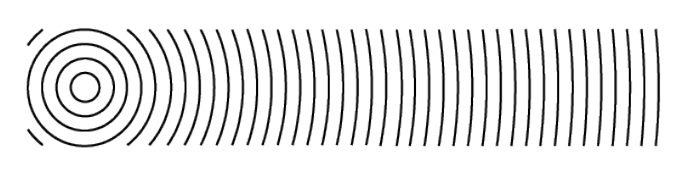
Usando notación compleja tenemos para la onda que se propaga hacia afuera:

\[U(r, t) = Re [ U(r)e^{−iωt}] = Re[\dfrac{A}{r}e^{i(kr−iωt)}] \nonumber \]

con U (r) = A exp (ikr) /r y A = A exp (iφ), donde φ es el argumento y A el módulo del número complejo A.

En la Figura\(\PageIndex{2}\) y Figura se muestran frentes de onda\(\PageIndex{3}\) esféricos. Para un observador que se encuentra a gran distancia de la fuente, la onda esférica parece una onda plana que se propaga desde la fuente hacia el observador (o en dirección opuesta, si hay un sumidero).