1.7: Ecuaciones Maxwell armónicas en el tiempo en la materia

Ahora volvemos a las ecuaciones de Maxwell y consideramos los campos electromagnéticos armónicos de tiempo, porque estos son, con mucho, los campos más importantes en óptica. Usando notación compleja tenemos

\[E(r, t) = Re [ E(r)e^{−iωt}], \nonumber \]

con E _x (r) = |E _x (r) |e ^{iΦx (r)}, E _y (r) = |E _y (r) |e ^{iφ (r)}, E _z (r) = |E _z (r) |e ^{iφ (r)}, donde φ _x (r) es el argumento del número complejo E _x (r) etc. Con notaciones similares para el campo magnético, obtenemos por sustitución en las ecuaciones de Maxwell (1.3.12), (1.3.13), (1.3.14) y (1.3.15), el tiempo-armónico Maxwell ecuaciones para los campos complejos:

\[∇ × E = iωµ_{0}H, Faraday’s\space Law \nonumber \]

\[∇ × H = −iωεE + σE + J_{ext}, Maxwell’s\space Law \nonumber \]

\[∇ · ε E = ρ_{ ext}, Gauss’s\space Law \nonumber \]

\[∇ · H = 0, no\space magnetic\space charge \nonumber \]

donde la derivada de tiempo ha sido reemplazada por la multiplicación de los campos complejos por −iω.

En las ecuaciones de Maxwell armónico de tiempo, la conductividad a veces se incluye en la parte imaginaria de la permitividad:

\[E= E_{ 0} [ 1 + χ_{e} + i\dfrac{σ}{ω}]. \nonumber \]

Si bien es conveniente hacer esto en la Ley de Maxwell (\(\PageIndex{3}\)), hay que recordar que en la Ley de Gauss (\(\PageIndex{4}\)), se debe seguir utilizando la permitividad original: _{E = 1 + χ e}. Cuando no hay fuentes externas: ρ _ext = 0 y el material es homogéneo (es decir, χ _e y σ son independientes de la posición), entonces (\(\PageIndex{4}\)) es equivalente a

\[∇ · E = 0. \nonumber \]

De ahí que en este (importante) caso especial, la definición (\(\PageIndex{6}\)) para la permitividad se pueda utilizar de manera segura sin riesgo de confusión.

Vemos que cuando usamos definition (\(\PageIndex{6}\)), la conductividad hace que la permitividad sea compleja y dependiendo de la frecuencia. Pero en realidad, también para aisladores (σ = 0), la permitividad E depende en general de la frecuencia y es compleja con una parte imaginaria positiva. La parte imaginaria positiva de E es una medida de la absorción de la luz por el material. La propiedad de que la permitividad depende de la frecuencia se llama dispersión. Excepto cerca de una frecuencia de resonancia, la parte imaginaria de E (ω) es pequeña y la parte real es una función de frecuencia que aumenta lentamente. A esto se le llama dispersión normal. Esto se ilustra con el índice de refracción de diferentes vidrios mostrados en la Figura\(\PageIndex{1}\)

Cerca de una resonancia, la parte real está cambiando rápidamente y disminuye con ω (este comportamiento se llama dispersión anómala), mientras que la parte imaginaria tiene un máximo a la frecuencia de resonancia del material, correspondiente a la absorción máxima a una resonancia como se ve en la Figura\(\PageIndex{2}\) At óptica frecuencias, la dispersión en su mayoría normal ocurre y para bandas de frecuencia pequeña como en la luz láser, a menudo es suficientemente precisa para usar el valor de la permitividad y la conductividad en la frecuencia central de la banda.

Figura\(\PageIndex{1}\): Parte real n ² − κ ² y parte imaginaria 2nκ de la permitividad E = (n + iκ) ², en función de longitud de onda y de frecuencia cerca de una resonancia.

Figura\(\PageIndex{2}\): Índice de refracción en función de la longitud de onda para varios tipos de vidrio (de Wikimedia Commons por Geek3/CC BY-SA).

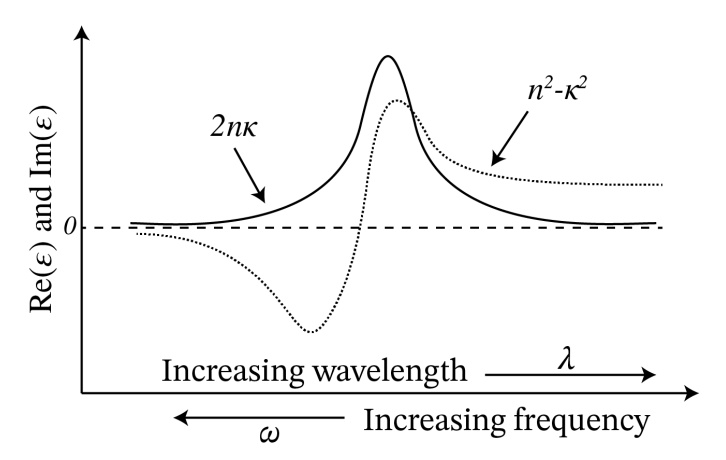
En muchos libros se utiliza la siguiente notación: E = (n + iκ) ², donde n y κ (“kappa”, que no debe confundirse con el número de onda k) son tanto reales como positivos, con n el índice de refracción y κ una medida de la absorción. Entonces tenemos Re (E) = n ² − κ ² e Im (E) = 2nκ (ver Figura\(\PageIndex{1}\)). Tenga en cuenta que aunque n y κ son ambos positivos, Re (E) puede ser negativo para algunas frecuencias. Esto sucede para los metales en la parte visible del espectro.

Observación. Cuando E depende de la frecuencia, las ecuaciones de Maxwell (1.3.13) y (1.3.14) para campos que no son armónicos de tiempo pueden, estrictamente hablando, no ser válidas, porque no está claro qué valor de E correspondiente a qué frecuencia se debe elegir. De hecho, en el caso de dispersión fuerte, los productos E ε deben ser reemplazados por circunvoluciones en el dominio del tiempo. Dado que casi siempre consideraremos campos con una banda de frecuencia estrecha, no vamos a dar más detalles sobre este tema.

1.6.1 Ondas planas electromagnéticas armónicas de tiempo

En esta sección asumimos que el material en el que se propaga la onda tiene conductividad que desaparece: σ = 0, no absorbe la luz y es homogéneo, es decir, que la permitividad E es una constante real. Además, asumimos que en la región del espacio de interés no hay fuentes. Estos supuestos implican en particular que (\(\PageIndex{7}\)) sostiene. El campo eléctrico de una onda plana armónica de tiempo viene dado por

\[E(r, t) = Re [ E(r)e^{−iωt}], \nonumber \]

con

\[E(r) = Ae^{ik·r}, \nonumber \]

donde A es un vector complejo constante (es decir, es independiente de la posición y el tiempo):

\[A = A_{x}\hat{x}+ A_{y}\hat{y} + A_{z}\hat{z}, \nonumber \]

con Ax = |Ax|E ^iϕx etc.. El vector de onda k satisface (1.5.7). La sustitución de (\(\PageIndex{9}\)) en (\(\PageIndex{7}\)) implica que

\[E(r) · k=0 \nonumber \]

para todos r y por lo tanto (\(\PageIndex{8}\)) implica que también el campo eléctrico real físico está en cada punto r perpendicular al vector de onda: ε (r, t) · k = 0. Por simplicidad ahora elegimos el vector de onda en la dirección del eje z y asumimos que el vector de campo eléctrico es paralelo al eje x. Este caso se llama onda electromagnética polarizada x. El campo complejo se escribe entonces como

\[E(x)=Ae^{ikz}\hat{x}, \nonumber \]

donde k = ω (Eµ ₀) ^1/2 y A = |A| exp (iϕ). De la Ley de Faraday (\(\PageIndex{2}\)) se desprende que

\[H(z)=\dfrac{k}{ωµ_{0}}\hat{z}×\hat{x}Ae^{ikz}=(\dfrac{E}{µ_{0}})^{1/2}Ae^{ikz}\hat{y}. \nonumber \]

El campo electromagnético real es así:

\[ε(z, t) = Re [ E(z)e^{−iωt}] = |A| cos(kz − ωt + ϕ)\hat{x}, \nonumber \]

\[H(z, t) = Re [ H(z)e^{−iωt}] =(\dfrac{E}{µ_{0}})^{1/2}|A| cos(kz − ωt + ϕ)\hat{y}. \nonumber \]

Concluimos que en un medio sin pérdidas, el campo eléctrico y magnético de una onda plana están en fase y en cada punto y en cada instante perpendiculares al vector de onda y entre sí. Como se ilustra en la Figura\(\PageIndex{3}\), en cualquier punto dado tanto el campo eléctrico como el magnético logran sus valores máximo y mínimo al mismo tiempo.

Figura\(\PageIndex{3}\): Los vectores armónicos de tiempo ε y H de una onda polarizada plana son perpendiculares entre sí y a la dirección del vector de onda que es también la dirección de ε × H.

1.6.2 Campo de un dipolo eléctrico

Otra solución importante de la ecuación de Maxwell es el campo irradiado por un dipolo eléctrico armónico de tiempo, es decir, dos cargas opuestas con igual fuerza que se mueven armónicamente en el tiempo alrededor de su centro de masa total. En esta sección el medio es homogéneo, pero puede absorber parte de la luz, es decir, la permitividad puede tener una parte imaginaria distinta de cero. Un dipolo eléctrico es el modelo electromagnético clásico para un átomo o molécula. Debido a que la longitud de onda óptica es mucho mayor que un átomo de molécula, estas cargas pueden considerarse concentradas tanto en el mismo punto r ₀. Las densidades de carga y corriente de dicho dipolo elemental son

\[ρ = −p · ∇δ(r − r_{0}), \nonumber \]

\[J = −iωpδ(r − r_{0}), \nonumber \]

con p el vector dipolo, definido por

\[p = qa, \nonumber \]

donde q > 0 es la carga positiva y a es el vector de posición del positivo con respecto a la carga negativa.

El campo irradiado por un dipolo eléctrico es muy importante. Es la solución fundamental de las ecuaciones de Maxwell, en el sentido de que el campo irradiado por una distribución arbitraria de fuentes siempre puede escribirse como una superposición de los campos de dipolos eléctricos elementales. Esto se deduce del hecho de que las ecuaciones de Maxwell son lineales y cualquier distribución de corriente puede escribirse como una superposición de corrientes dipolares elementales.

El campo irradiado por un dipolo elemental en r ₀ en materia homogénea puede calcularse analíticamente y está dado por

\[E(r) = [ k2 \hat{R} × ( p × \hat{R}) + ( 3 \hat{R} · p \hat{R} − p) ( \dfrac{1}{R^2} − \dfrac{ik}{R} )]\dfrac{e^{ikR}}{4πER}, \nonumber \]

\[H(r) =\dfrac{k^2c}{n}(1 +\dfrac{ik}{R})\hat{R} × p\dfrac{e^{ikR}}{4πR}, \nonumber \]

donde k = k ₀, n = (E/E ₀) ^1/2, con k ₀ el número de onda en vacío y con R = r − r ₀. Se observa que los campos eléctricos y magnéticos complejos son proporcionales a la onda esférica compleja: e ^{IKr /R} discutida en la Sección 1.5.3, pero que estos campos contienen factores adicionales dependientes de la posición. En particular, a gran distancia al dipolo:

\[H(r) ≈\dfrac{k^2c}{n}\hat{R} × p\dfrac{e^{ikR}}{4πR}, \nonumber \]

\ [E (r) ≈k^2\ hat {R} × (p ×\ hat {R})\ dfrac {e^ {IKr}} {4πer} =- (\ dfrac {μ_ {0}} {E})\ hat {R} × H (r).

Figura\(\PageIndex{4}\): Líneas de campo eléctrico y magnético creadas por un dipolo radiante (de Wikimedia Commons, JPG original debido a Averse, SVG de Maschen./CC0).

En la Figura\(\PageIndex{4}\) se dibujan las líneas de campo eléctrico y magnético de un dipolo radiante. Para un observador a gran distancia del dipolo, los campos eléctrico y magnético son perpendiculares entre sí y perpendiculares a la dirección de la línea de visión R desde el dipolo hasta el observador. Además, el campo eléctrico se encuentra en el plano a través del vector dipolo p y el vector R, mientras que el campo magnético es perpendicular a este plano. Entonces, para un observador distante el campo dipolar es similar al de una onda plana que se propaga desde el dipolo hacia el observador y tiene un campo eléctrico paralelo al plano a través del dipolo y la línea de visión R y perpendicular a R. Además, las amplitudes de los campos eléctrico y magnético dependen de la dirección de la línea de visión, desapareciendo el campo cuando la línea de visión R es paralela al vector dipolo p y con amplitud máxima cuando R está en el plano perpendicular al dipolo vector. Este resultado concuerda con el conocido patrón de radiación de una antena cuando la corriente del dipolo está en la misma dirección que la de la antena.