6.6: Aproximaciones de Fresnel y Fraunhofer

La aproximación de Fresnel y Fraunhofer son dos aproximaciones de la integral Rayleigh-Sommerfeld (6.13). Las aproximaciones se basan en el supuesto de que el campo se ha propagado a lo largo de una distancia suficientemente grande\(z\). En la aproximación de Fraunhofer,\(z\) tiene que ser muy grande, es decir, mucho más grande que para que se mantenga la aproximación de Fresnel. Dicho de otra manera: en orden de más preciso a menos preciso (es decir, solo válido para grandes distancias de propagación), las integrales de difracción se clasificarían como:

[Más preciso]\(\quad\) Rayleigh-Sommerfeld\(\rightarrow\) Fresnel\(\rightarrow\) Fraunhofer\(\quad\) [Menos preciso].

Figura\(\PageIndex{1}\): Demostración de los roles de diferentes frecuencias espaciales. Al eliminar las altas frecuencias espaciales, solo quedan las amplias características de la imagen: perdemos resolución. Si se eliminan las frecuencias espaciales bajas, solo quedan las características nítidas (es decir, los contornos) en la imagen.

Figura\(\PageIndex{2}\): Demostración del papel de la fase de la transformada espacial de Fourier. Si se elimina la información de amplitud, pero se mantiene la información de fase, algunas características de la imagen original aún son reconocibles. Sin embargo, si se elimina la información de fase pero se mantiene la información de amplitud, la imagen original se pierde por completo.

6.5.1 Aproximación de Fresnel

Para ambas aproximaciones, suponemos que\(z\) en la Ec. (6.3.1) es tan grande que en el denominador podemos aproximar\(r \approx z\)\[\begin{aligned} U(x, y, z) &=\frac{1}{i \lambda} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) \frac{z}{r} \frac{e^{i k r}}{r} \mathrm{~d} x^{\prime} \mathrm{d} y^{\prime} \\ & \approx \frac{1}{i \lambda z} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) e^{i k r} \mathrm{~d} x^{\prime} \mathrm{d} y^{\prime} . \end{aligned} \nonumber \]

La razón por la que no podemos aplicar la misma aproximación para\(r\) en el exponente, es que\(r\) se multiplica por\(k=2 \pi / \lambda\), que es muy grande, por lo que cualquier error introducido por aproximación se\(r\) magnificaría significativamente por \(k\)y luego puede conducir a un valor completamente diferente de\(\exp (i k r)=\cos (k r)+i \sin (k r)\). Para\(\exp (i k r)\) aproximarnos\(r\) en el exponente hay que tener más cuidado y en su lugar aplicar una expansión de Taylor. Recordemos que\[\begin{aligned} r &=\sqrt{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}+z^{2}} \\ &=z \sqrt{\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{z^{2}}+1} . \end{aligned} \nonumber \]

Sabemos que por un número pequeño\(s\) podemos expandirnos\[\sqrt{s+1}=1+\frac{s}{2}-\frac{s^{2}}{8}+\ldots . \nonumber \]

Ya que asumimos que\(z\) es grande,\(\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{z^{2}}\) es pequeño, así podemos expandirnos\[\begin{aligned} r &=z \sqrt{\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{z^{2}}+1} \\ & \approx z\left(1+\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{2 z^{2}}\right) \\ &=z+\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{2 z}, \quad \text { Fresnel approximation. } \end{aligned} \nonumber \]

Con esta aproximación, llegamos a la integral de difracción de Fresnel, que puede escribirse en las siguientes formas equivalentes:\[\begin{aligned} U(x, y, z) & \approx \frac{e^{i k z}}{i \lambda z} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) e^{\frac{i k}{2 z}\left[\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}\right]} \mathrm{d} x^{\prime} \mathrm{d} y^{\prime} \\ &=\frac{e^{i k z} e^{\frac{i k\left(x^{2}+y^{2}\right)}{2 z}}}{i \lambda z} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) e^{\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}} e^{-i k\left(\frac{x}{z} x^{\prime}+\frac{y}{z} y^{\prime}\right)} \mathrm{d} x^{\prime} \mathrm{d} y^{\prime} \\ &=\frac{e^{i k z} e^{\frac{i k\left(x^{2}+y^{2}\right)}{2 z}}}{i \lambda z} \mathcal{F}\left\{U_{0}\left(x^{\prime}, y^{\prime}\right) e^{\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}}\right\}\left(\frac{x}{\lambda z}, \frac{y}{\lambda z}\right) . \end{aligned} \nonumber \]

Especialmente la última expresión es interesante, porque demuestra que

La integral de Fresnel es la transformada de Fourier del campo\(U_{0}\left(x^{\prime}, y^{\prime}\right)\) multiplicada por el propagador de Fresnel\(\exp \left(\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}\right)\).

Tenga en cuenta que este propagador depende de la distancia de propagación\(z\).

Observación. Mediante la transformación de Fourier\((\(\PageIndex{6}\))\), se obtienen las amplitudes de onda plana de la integral de Fresnel. Resulta que estas amplitudes son iguales a\(\mathcal{F}\left(U_{0}\right)\) multiplicarse por un factor de fase. Este factor de fase es una aproximación paraxial del factor de fase exacto dado por\(\exp \left(i z k_{z}\right)\), es decir, contiene como exponente la aproximación parabólica de\(k_{z}\). Por lo tanto, la aproximación de Fresnel también se llama aproximación paraxial. De hecho, se puede demostrar que la integral de difracción de Fresnel es una solución de la ecuación de onda paraxial y a la inversa, que cada solución de la ecuación de onda paraxial puede escribirse como una integral de difracción de Fresnel.

6.5.2 Aproximación de Fraunhofer

Para la aproximación de Fraunhofer, haremos una aproximación más a\(r\) in\(\exp (i k r)\)\[\begin{aligned} r & \approx z+\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{2 z} \text { Fresnel approximation } \\ & \approx z+\frac{x^{2}+y^{2}-2 x x^{\prime}-2 y y^{\prime}}{2 z} \text { Fraunhofer approximation. } \end{aligned} \nonumber \]

De ahí que se hayan omitido los términos cuadráticos\(x^{\prime 2}+y^{\prime 2}\), y comparados con respecto a la integral de difracción de Fresnel, simplemente omitimos el factor\(\exp \left(\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}\right)\) para obtener la integral de difracción de Fraunhofer:\[U(x, y, z) \approx \frac{e^{i k z} e^{\frac{i k\left(x^{2}+y^{2}\right)}{2 z}}}{i \lambda z} \mathcal{F}\left(U_{0}\right)\left(\frac{x}{\lambda z}, \frac{y}{\lambda z}\right) \nonumber \]

Esto lleva a la siguiente observación importante:

El campo lejano de Fraunhofer\(U_{0}\left(x^{\prime}, y^{\prime}\right)\) es simplemente su transformada de Fourier con un factor de fase cuadrático adicional.

Tenga en cuenta que las coordenadas para las que tenemos que evaluar la\(\mathcal{F}\left(U_{0}\right)\) escala con\(1 / z\), y el campo general\(U(x, y, z)\) es proporcional a\(1 / z\). Esto significa que a medida que eliges\(z\) más grande (es decir, propaga el campo más lejos), el campo simplemente se extiende sin cambiar su forma, y su amplitud disminuye. Dicho de otra manera, aparte del factor\(1 / z\) frente a la integral, el campo Fraunhofer solo depende de los ángulos\(x / z\) amd\(y / z\). Por lo tanto, el campo diverge a medida que\(z\) aumenta la distancia de propagación.

Finalmente, para distancias de propagación suficientemente grandes, es decir, en el límite de Fraunhofer, la luz siempre se extiende sin cambiar la forma de la distribución de la luz.

Observaciones.

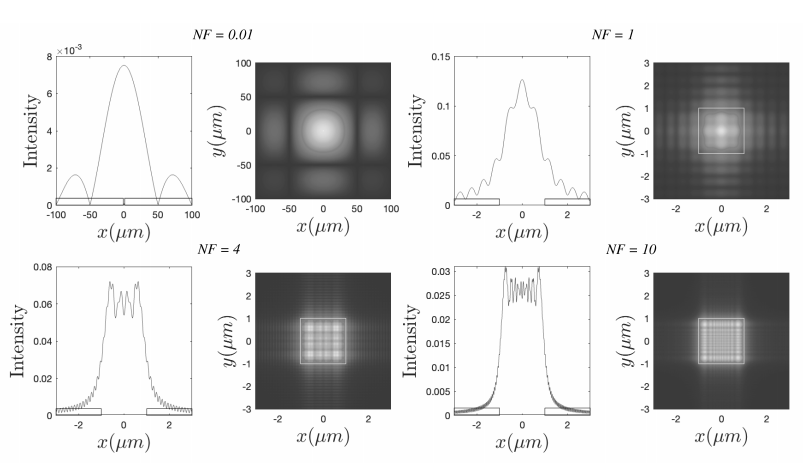
1. La integral de Fresnel es, al igual que la integral de Fraunhofer, también una transformada de Fourier, evaluada en frecuencias espaciales que dependen del punto de observación:\[\xi=\frac{x}{\lambda z}, \quad \eta=\frac{y}{\lambda z} . \nonumber \] Sin embargo, en contraste con la integral de Fraunhofer, la integral de Fresnel depende adicionalmente de una manera diferente de la distancia de propagación \(z\), es decir, a través del epxonente del propagador en el integrando. Esta es la razón por la que la integral de Fresnel no solo depende\(z\) a través de las proporciones\(x / z\) y\(y / z\) sino de una manera más complicada. Por lo tanto, la integral de Fresnel da patrones bastante diversos dependiendo del valor de la distancia de propagación\(z\), como se muestra en la Figura\(\PageIndex{4}\).
2. \(f_{a, b}(x, y)=f(x-a, y-b)\)Sea la función obtenida de\(f\) por traducción. De la propiedad general de la transformada de Fourier:\[\mathcal{F}\left(f_{a, b}\right)(\xi, \eta)=e^{-2 \pi i(\xi a+\eta b)} \mathcal{F}(f)(\xi, \eta) . \nonumber \] De ahí que cuando\(U_{0}\) se traduce el campo, no se cambia la intensidad en el campo lejano de Fraunhofer. En contraste, debido al factor de fase cuadrático adicional en el integrando de la integral de Fresnel, la intensidad del campo de Fresnel en general cambia cuando\(U_{0}\) se traduce.
3. Supongamos que\(U_{0}\) es el campo inmediatamente detrás de una abertura\(\mathcal{A}\) con diámetro\(D\) en una pantalla opaca. Entonces se puede demostrar que los puntos\((x, y, z)\) de observación, para los cuales las integrales de difracción de Fresnel y Fraunhofer son suficientemente precisas, satisfacen:\[\begin{aligned} &\frac{z}{\lambda}>\left(\frac{\max _{\left(x^{\prime}, y^{\prime}\right) \in \mathcal{A}} \sqrt{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}}{\lambda}\right)^{4 / 3} \text {, Fresnel } \\ &\frac{z}{\lambda}>\left(\frac{D}{\lambda}\right)^{2} \text {, Fraunhofer } \end{aligned} \nonumber \] Supongamos que\(D=1 \mathrm{~mm}\) y la longitud de onda es luz verde:\(\lambda=550 \mathrm{~nm}\), luego la aproximación de Fraunhofer es exacto si\(z>2 \mathrm{~m}\). La desigualdad (\(\PageIndex{6}\)) es suficiente para que la fórmula de Fresnel sea precisa, pero no siempre es necesaria. A menudo, la aproximación de Fresnel ya es precisa para distancias de propagación más pequeñas.
4. Los puntos de observación donde se pueden utilizar las fórmulas de Fraunhofer deben en todo caso satisfacer:\[\frac{x}{z}<1, \quad \frac{y}{z}<1 . \nonumber \] Cuando\(x / z>1\), la frecuencia espacial\(k_{x}=\frac{2 \pi x}{z \lambda}>k\) asociada a este punto corresponde a una onda evanescente. Obviamente, una onda evanescente no puede contribuir al campo lejano de Fraunhofer porque disminuye exponencialmente con la distancia\(z\).
5. En cualquier expresión para un campo óptico, siempre se pueden omitir factores de fase constante, es decir, una fase global que no depende de la posición. Si uno solo está interesado en el campo en ciertos planos\(z=\) constantes, entonces también se\(\exp (i k z)\) puede omitir un factor como. Además, en algunos casos también se omite un factor de fase dependiente de la posición frente a las integrales de difracción de Fresnel y Fraunhofer, es decir, cuando solo la intensidad es de interés. En los ejercicios suele mencionarse que este factor puede omitirse: si esto no se afirma, debe conservarse en las fórmulas.

Figura\(\PageIndex{3}\): Demostración del principio de incertidumbre. Cuanto más confinado\(U(x, y)\) es, mayor es la propagación de\(\mathcal{F}(U)\left(\frac{k_{x}}{2 \pi}, \frac{k_{y}}{2 \pi}\right)\).

Figura\(\PageIndex{4}\): Ejemplo de intensidades de campos de Fresnel de una abertura cuadrada, mostrados como contornos y en sección transversal para diferentes distancias que aumentan de la parte inferior derecha a la superior izquierda. El patrón superior izquierdo es igual al patrón Fraunhofer. \(N_{F}=D^{2} / \lambda z\)es el número de Fresnel y\(\lambda=600 \mathrm{~nm} .\)

6.5.3 Ejemplos de campos Fresnel y Fraunhofer

Aproximación de Fresnel del campo de dos fuentes puntuales.

Considere dos fuentes puntuales en\(\mathbf{r}_{s}^{+}=(a / 2,0,0)\) y\(\mathbf{r}_{s}^{-}=(-a / 2,0,0)\). Los campos de cada uno de ellos en un punto\(\mathbf{r}=(x, y, z)\) están dados por (5.6.2)\[U_{\pm}(\mathbf{r})=\frac{e^{i k\left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right|}}{\left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right|} \nonumber \]

Aplicamos la aproximación Fresnel para grandes\(z\):\[\begin{aligned} \left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right| &=z \sqrt{1+\frac{(x \mp a / 2)^{2}+y^{2}}{z^{2}}} \\ & \approx z+\frac{(x \mp a / 2)^{2}+y^{2}}{2 z} \\ &=z+\frac{x^{2}+y^{2}+a^{2} / 4}{2 z} \mp \frac{a x}{2 z} . \end{aligned} \nonumber \]

De ahí,\[U_{\pm}(\mathbf{r}) \approx \frac{e^{i k z}}{z} e^{i k \frac{x^{2}+y^{2}}{2 z}} e^{i k \frac{a^{2}}{8 z}} e^{\mp i k \frac{a x}{2 z}}, \nonumber \] donde en el denominador sustituimos\(\left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right|\) por\(z\). Obsérvese que la aproximación de Fraunhofer equivale a\(e^{i k a^{2} /(8 z)} \approx 1\) mientras\(e^{i k \frac{x^{2}+y^{2}}{2 z}}\) permanece el factor de fase. La intensidad en una pantalla\(z=\) constante del campo total es\[\begin{aligned} I_{\text {tot }}(\mathbf{r}) &=\left|U_{+}(\mathbf{r})+U_{-}(\mathbf{r})\right|^{2}=\frac{1}{z^{2}}\left|e^{-i k \frac{a x}{2 z}}+e^{i k \frac{a x}{2 z}}\right|^{2} \\ &=\frac{2}{z^{2}}\left[1+\cos \left(2 \pi \frac{a x}{\lambda z}\right)\right] \end{aligned} \nonumber \]

Se observa que la intensidad resulta de la interferencia de dos ondas planas:\(\exp [\pm i k a x /(\lambda z)]\) y viene dada por una función coseno (ver Figura\(\PageIndex{5}\)). Tenga en cuenta que para dos fuentes puntuales, el patrón de intensidad es el mismo en la aproximación de Fresnel y Fraunhofer. Sin embargo, esto es especial para dos fuentes puntuales: cuando se consideran más de dos fuentes puntuales, los patrones de Fresnel y Fraunhofer son diferentes. El patrón de intensidad es independiente de\(y\), y desaparece en las líneas\[\frac{x}{z}=(2 m+1) \frac{\lambda}{2 a} \nonumber \] y tiene máximos en las líneas\[\frac{x}{z}=m \frac{\lambda}{a}, \nonumber \] para enteros\(m\).

Campo de Fraunhofer de una abertura rectangular en una pantalla.

Deja que la pantalla sea\(z=0\) y la apertura sea dada por\(-a / 2<x<a / 2,-b / 2<y<b / 2\). La función de transmisión\(\tau(x, y)\) es:\[\tau(x, y)=1_{[-a / 2, a / 2]}(x) 1_{[-b / 2, b / 2]}(y), \nonumber \] dónde\[1_{[-a / 2, a / 2]}(x)=\left\{\begin{array}{l} 1, \text { if }-\frac{a}{2} \leq x \leq \frac{a}{2}, \\ 0, \text { otherwise }, \end{array}\right. \nonumber \] y de manera similar para\(1_{[-b / 2, b / 2]}(y)\). Deje que la hendidura sea iluminada por una onda plana incidente perpendicular con amplitud unitaria. Entonces el campo inmediatamente detrás de la pantalla es:\[U_{0}(x, y)=\tau(x, y)=1_{[-a / 2, a / 2]}(x) 1_{[-b / 2, b / 2]}(y), \nonumber \] Tenemos\[\begin{aligned} \mathcal{F}\left(1_{[-a / 2, a / 2]}\right)(\xi) &=\int_{-a / 2}^{a / 2} e^{-2 \pi i \xi x} \mathrm{~d} x \\ &=\frac{e^{\pi i a \xi}-e^{-\pi i a \xi}}{2 \pi i \xi} \\ &=a \frac{\sin (\pi a \xi)}{\pi a \xi} \\ &=a \operatorname{sinc}(\pi a \xi), \end{aligned} \nonumber \] donde\(\operatorname{sinc}(u)=\sin (u) / u\). De ahí\[\mathcal{F}\left(U_{0}\right)\left(\frac{x}{\lambda z}, \frac{y}{\lambda z}\right)=a b \operatorname{sinc}\left(\frac{\pi a x}{\lambda z}\right) \operatorname{sinc}\left(\frac{\pi b y}{\lambda z}\right) . \nonumber \] que el campo lejano de Fraunhofer de una abertura rectangular en un plano a gran distancia\(z\) se obtiene sustituyendo (\(\PageIndex{25}\)) en (\(\PageIndex{9}\)).

Figura\(\PageIndex{5}\): Patrón de intensidad de Fraunhofer de dos fuentes puntuales coherentes\(200 \mathrm{~nm}\) separadas (círculos), de igual fuerza para\(\lambda=600 \mathrm{~nm}\).

Observaciones.

1. El primer cero a lo largo de la\(x\) dirección -desde el centro\(x=0\) ocurre para\[x=\pm \frac{\lambda z}{a} . \nonumber \] La distancia entre los dos primeros ceros a lo largo del\(x\) eje es\(2 \lambda z / a\) y por lo tanto es mayor cuando el ancho a lo largo de la\(x\) -dirección de la abertura es más pequeña.
2. Las desigualdades (\(\PageIndex{14}\)) implican que cuando\(a<\lambda\), el patrón de campo lejano no tiene ceros en función de\(x\). Entonces es difícil o incluso imposible deducir el ancho\(a\) de la intensidad de Fraunhofer. Esto es una ilustración del hecho de que la información sobre tamaños menores que la longitud de onda no puede propagarse al campo lejano.
3. Como se muestra en la Figura\(\PageIndex{6}\), el patrón de difracción de Fraunhofer en función del ángulo de difracción es más estrecho en la dirección en la que la abertura es más ancha.

Figura\(\PageIndex{6}\): Patrón de difracción de Fraunhofer de una abertura rectangular en una pantalla opaca. En a) el ancho de la abertura en la\(y\) dirección -es el doble que en la\(x\) dirección. En b) el ancho en la\(y\) dirección -es 10 veces que en la\(x\) dirección -.

Matriz periódica de ranuras

Ahora podemos predecir cómo será el patrón de difracción de una serie de hendiduras de ancho finito. Del patrón de Fraunhofer de una sola abertura rectangular se deduce que, si los lados paralelos a una dirección a son muy largos, el patrón de difracción de Fraunhofer en función del ángulo en esa dirección es muy estrecho. En la Figura\(\PageIndex{6}\) b se muestra el patrón de difracción de Fraunhofer de una abertura rectangular, de la cual el ancho en la\(y\) dirección es 10 veces el\(x\) de la dirección. El patrón de difracción se concentra entonces fuertemente a lo largo del\(x\) eje. Si solo consideramos el patrón de Fraunhofer\(y / z=0\) mientras aún lo consideramos como una función de\(x / z\), basta con calcular la transformada de Fourier solo con respecto a\(x\). El problema se convierte entonces en un problema de difracción para una hendidura unidimensional.

Consideramos ahora una matriz de tales hendiduras de las cuales los lados largos son todos paralelos al\(y\) eje -y descuidan a partir de ahora la\(y\) variable -. Supongamos que\(W_{\text {slit }}(x)\) es una función de bloque que describe la función de transmisión de una sola hendidura. Definimos el peine Dirac por\[\mathrm{II}_{\Delta}(x)=\sum_{m=-\infty}^{\infty} \delta(x-m \Delta) . \nonumber \]

Entonces la función de transmisión de una serie infinita de hendiduras con ancho finito viene dada por la convolución\(\mathrm{II}_{\Delta}(x) * W_{\text {slit }}(x)\). Para que el número de ranuras sea finito, multiplicamos la expresión con otra función de bloque\(W_{\text {array }}(x)\) y obtenemos\[\tau(x)=\left(\mathrm{II}_{\Delta}(x) * W_{\text {slit }}(x)\right) W_{\text {array }}(x) . \nonumber \]

El patrón de difracción en el campo lejano viene dado por la transformada de Fourier del campo cercano transmitido. Si la iluminación incidente es una onda plana perpendicular con amplitud unitaria, el campo cercano transmitido es simplemente\(\tau(x)\). Usando el hecho de que las circunvoluciones en el espacio real corresponden a productos en el espacio de Fourier y viceversa, y usando el hecho de que\[\mathcal{F}\left\{\mathrm{W}_{\Delta}(x)\right\}=(1 / \Delta) \mathrm{W}_{1 / \Delta}(\xi), \nonumber \] ver Apéndice (E.9) y (E.10), encontramos\[\mathcal{F}(\tau)=\frac{1}{\Delta}\left[\mathrm{W}_{1 / \Delta} \mathcal{F}\left(W_{\text {slit }}\right)\right] * \mathcal{F}\left(W_{\text {array }}\right). \nonumber \]

Si la rendija tiene ancho\(a\):\[\begin{aligned} \frac{1}{\Delta} \mathrm{I}_{1 / \Delta} \mathcal{F}\left(W_{\text {slit }}\right)(\xi) &=\frac{a}{\Delta} \sum_{m=-\infty}^{\infty} \delta\left(\xi-\frac{m}{\Delta}\right) \operatorname{sinc}(\pi a \xi) \\ &=\frac{a}{\Delta} \sum_{m=-\infty}^{\infty} \operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right) \delta\left(\xi-\frac{m}{\Delta}\right) . \end{aligned} \nonumber \]

Si el ancho total de la matriz es\(A\), entonces\[\mathcal{F}\left(W_{\text {array }}\right)(\xi)=A \operatorname{sinc}(\pi A \xi), \nonumber \] y concluimos que\[\mathcal{F}(\tau)(\xi)=\frac{a A}{\Delta} \sum_{m=-\infty}^{\infty} \operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right) \operatorname{sinc}\left(\pi A\left(\xi-\frac{m}{\Delta}\right)\right) . \nonumber \]

El campo Fraunhofer de la matriz de ranuras es (omitiendo el factor de fase cuadrático):\[\mathcal{F}(\tau)\left(\frac{x}{\lambda z}\right)=\frac{a A}{\Delta} \sum_{m=-\infty}^{\infty} \operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right) \operatorname{sinc}\left(\pi A\left(\frac{x}{\lambda z}-\frac{m}{\Delta}\right)\right) . \nonumber \]

Para las direcciones\[\frac{x}{z}=\theta_{m}=\frac{m \lambda}{\Delta}, \quad m=0, \pm 1, \pm 2, \ldots, \quad \text { diffraction orders } \nonumber \] el campo tiene máximos locales (picos). Estas direcciones se llaman órdenes de difracción. Obsérvese que como se explicó anteriormente, se debe sostener:\(x / z<1\) en el campo lejano de Fraunhofer, que establece un límite al número de las órdenes difractadas que ocurren. Este límite depende del período y la longitud de onda y se define por:\[|m| \leq \Delta / \lambda . \nonumber \]

De ahí que cuanto mayor sea la relación entre el período y la longitud de onda, más órdenes de difracción.

El ancho de un orden de difracción viene dado por el ancho de la función (\(\PageIndex{31}\)), es decir, viene dado por\[\Delta \theta=\frac{\lambda}{A}, \quad \text { angular width of a diffraction order. } \nonumber \]

De ahí que cuanto más grandes\(A\), es decir, cuantas más hendiduras haya en la matriz, más estrechos serán los picos en los que se difracta la energía.

La propiedad (\(\PageIndex{34}\)) de que los ángulos de difracción de los órdenes dependen de la longitud de onda se utiliza para separar las longitudes de onda. Los espectrómetros de rejilla utilizan estructuras periódicas como esta matriz de ranuras para separar y medir longitudes de onda con mucha precisión. Por ejemplo, para una rejilla con 1000 periodos se puede obtener una resolución de\(\Delta \lambda / \lambda=10^{-3}\).

Las amplitudes de los órdenes difractados:\[\operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right), \nonumber \] están determinadas por el ancho de las hendiduras. Por lo tanto, la envolvente (es decir, grandes características) del patrón de difracción de Fraunhofer está determinada por las propiedades a pequeña escala de la matriz, es decir, el ancho de las ranuras. Esto se ilustra en la Figura\(\PageIndex{7}\). Observación. Una fila periódica de ranuras es un ejemplo de una rejilla de difracción. Una rejilla es una estructura periódica, es decir, la permitividad es una función periódica de la posición. Las estructuras pueden ser periódicas en una, dos y tres direcciones. Un cristal actúa como una rejilla tridimensional cuyo período es el período del cristal, es decir, unos pocos Angstrom. Las ondas electromagnéticas de longitud de onda igual a un Angstrom o menos se denominan rayos X. Cuando un haz de rayos X ilumina un cristal, un detector en el campo lejano mide el patrón de difracción de Fraunhofer dado por la intensidad de la transformada de Fourier del campo cercano refractado. Estos órdenes de difracción de cristales para rayos X fueron descubiertos por Von Laue y se utilizan para estudiar la estructura atómica de los cristales.

Figura\(\PageIndex{7}\): Ilustración de un patrón de difracción de una serie de cuatro ranuras.