6.7: Difracción de Fraunhofer revisitada

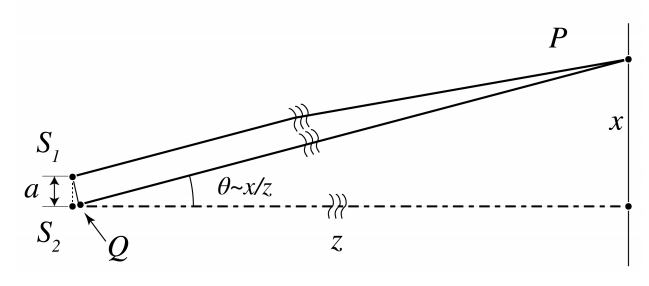
Los patrones de difracción de Fraunhofer pueden explicarse cualitativamente considerando direcciones en las que ocurre la interferencia destructiva y constructiva. Considere dos fuentes puntuales mutuamente coherentes\(S_{1}, S_{2}\) en el\(x\) eje como se muestra en la Figura\(\PageIndex{1}\). Suponemos que estas fuentes puntuales están en fase. En una pantalla a gran distancia se observa\(z\) un patrón de interferencia. Si la distancia\(z\) de la pantalla es muy grande, los frentes de onda esféricos emitidos por las fuentes puntuales son casi planos en la pantalla. En punto\(P\) en la pantalla a una distancia\(x\) por encima del\(z\) -eje las diferencias de trayectoria óptica de las ondas emitidas por las dos fuentes se dan aproximadamente por\(S_{2} Q=a \theta\), donde\(\theta=x / z\) se supone pequeñas. Por lo tanto, ocurre interferencia constructiva para ángulos\(\theta\) tales que\(S_{2} Q=m \lambda\) para algún número entero\(m\), es decir, cuando\[\theta=m \frac{\lambda}{a}, \quad \text { constructive interference. } \nonumber \]

La interferencia destructiva ocurre cuando la diferencia de longitud de ruta satisface\(S_{2} Q=\lambda / 2+m \lambda\) algún número entero\(m\), por lo tanto, para ángulos\[\theta=(m+1 / 2) \frac{\lambda}{a} \quad \text { destructive interference. } \nonumber \]

Si las fuentes puntuales tienen la misma fuerza, sus campos cancelan perfectamente para estos ángulos.

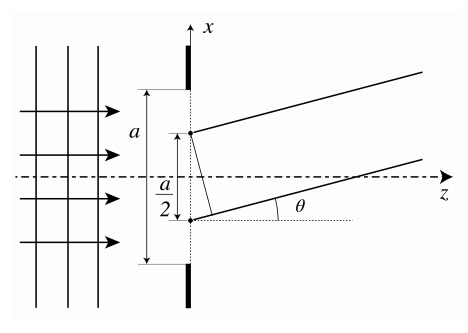
Consideremos ahora una hendidura como se muestra en la Figura la\(\PageIndex{2}\) cual está iluminada por una onda plana incidente perpendicular. Por el principio Huygens-Fresnel, el campo en una pantalla alejada de la hendidura es la suma de los campos de fuentes puntuales en la abertura. Dado que la hendidura está iluminada por una onda plana en incidencia perpendicular, todas las fuentes puntuales están en fase y tienen la misma fuerza. Divida la hendidura en dos mitades iguales como se muestra en la Figura\(\PageIndex{2}\). Las fuentes puntuales en la hendidura pueden disponerse en pares, de las cuales una fuente puntual está en la mitad superior de la hendidura y la otra en la posición equivalente (a\(a / 2\) distancia de la otra fuente puntual) en la mitad inferior de la hendidura. Dejar\(\theta\) ser un ángulo para el cual las dos fuentes puntuales de un par se cancelan entre sí es decir,\[\theta=(m+1 / 2) \frac{\lambda}{a / 2}=(1+2 m) \frac{\lambda}{a}, \nonumber \] ya que la distancia entre las fuentes puntuales es\(a / 2\). Al traducir el par de fuentes puntuales a través de las hendiduras, se deduce que ambas medias hendiduras se cancelan perfectamente entre sí para estos ángulos.

Figura\(\PageIndex{1}\): Interferencia de fuentes puntuales mutuamente coherentes. Para puntos\(z\) muy grandes\(P\) donde ocurre interferencia constructiva y destructiva son tales que para algún número entero\(m: S_{2} Q=m \lambda\) y\(S_{2} Q=(1 / 2+m) \lambda\), respectivamente

Figura\(\PageIndex{2}\): Dividiendo la hendidura en dos hendiduras de tamaño\(a / 2\) cada una y considerando pares de fuentes puntuales, de las cuales una está en la mitad de la hendidura y la otra en la posición correspondiente en la otra mitad, ángulos donde se produce interferencia destructiva entre estas fuentes puntuales conducen a mínimos en el patrón de difracción. Tenga en cuenta que las fuentes puntuales tienen posiciones correspondientes en las dos partes de la hendidura si su distancia es\(a / 2\).

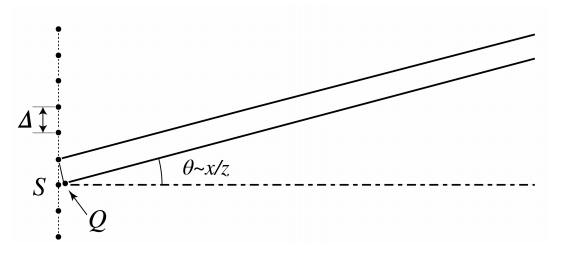
A continuación considere una rejilla de difracción con periodo\(\Delta\). De la Figura se deduce\(\PageIndex{3}\) que habrá interferencia constructiva entre períodos adyacentes, y por lo tanto para todos los períodos, para ángulos para los que la distancia\(S Q\) en la Fig\(\PageIndex{3}\) es un múltiplo de la longitud de onda, es decir, para los\[\theta=m \frac{\lambda}{\Delta} \text {, } \nonumber \] cuales corresponde a la dirección de la órdenes de difracción. Para otros ángulos las fases de los campos de los diferentes periodos difieren ampliamente y por lo tanto los campos casi se cancelan en estos ángulos.

Esto explica que para una rejilla de difracción que consta de muchos períodos, la intensidad del campo lejano es alta solo en direcciones particulares, dependiendo de la longitud de onda y el período de la rejilla.

Figura\(\PageIndex{3}\): Si el ángulo\(\theta\) es tal que\(S Q\) es un múltiplo de la longitud de onda, dos periodos adyacentes, y por lo tanto todos los períodos de la rejilla, interfieren constructivamente. Estos ángulos corresponden a los órdenes de difracción.