1.8: Forma Diferencial de la Ley de Snell

La ley de Snell en la forma\(n \sin \theta\) = constante es útil para calcular cómo se dobla un rayo de luz al viajar de un medio a otro donde hay un cambio discreto del índice de refracción. Si existe un medio en el que el índice de refracción cambia continuamente, puede ser útil una forma diferencial de la ley de Snell. Esto se obtiene simplemente por diferenciación de\(n \sin \theta\) = constante, para obtener la forma diferencial de la ley de Snell

\[ \cot \theta d \theta = -\frac{dn}{n}.\label{eq:1.9.1} \]

Si lo expresamos en términos del ángulo complementario\(\Psi\) (ver Figura I.24), esta ecuación toma la forma

\[ \tan\Psi d \Psi = \frac{dn}{n}.\label{eq:1.9.2} \]

Veamos cómo se podría usar esto. Supongamos, por ejemplo, que tenemos algún medio en el que el índice de refracción disminuye linealmente con la\(y\) coordenada según

\[ n = n_0 - \frac{(n_0-1)y}{a}. \label{eq:1.9.3} \]

Esta forma tiene\(n = n_0\) al\(y = 0\), disminuyendo linealmente a\(n = 1\) at\(y = a\). Suponemos que\(n = 1\) en todas partes más allá\(y = a\). La ecuación se simplifica si escribimos\(\mu\) para\(n −1\) y para\(\mu_0\) para\(n_0 −1\), de modo que

\[ \mu = \mu_0 \left(1 - \frac{y}{a}\right),\label{eq:1.9.4} \]

que tiene\(\mu\) decreciente linealmente de\(\mu_0\) a cero. Supongamos que dirigimos un rayo de luz hacia arriba desde el origen en una dirección que hace un ángulo\(\alpha\) con la horizontal, y deseamos trazar el rayo a través del medio a medida que el índice de refracción cambia continuamente. Ver Figura I.24. Con el índice de refracción cambiando como en la ecuación\(\ref{eq:1.9.4}\), la ley de Snell toma la forma

\[ tan \Psi d\Psi = -\frac{dy}{k-y}, \quad \text{where} \quad k = \frac{n_0a}{\mu_0}.\label{eq:1.9.5} \]

En la integración, esto se convierte

\[ y = k\left(1- \frac{\cos\alpha}{\cos\Psi}\right) \quad \text{or} \quad \cos\Psi = \frac{k\cos\alpha}{k-y}.\label{eq:1.9.6} \]

Esta es la\((y, \Psi)\) ecuación al camino que toma la luz. Se puede ver a partir de esta ecuación que el camino se vuelve horizontal cuando\(y = k(1 − \cos\alpha\). Para encontrar la\((x ,y)\) ecuación, utilizamos las identidades\( \cos\Psi = (1+\tan^2 \Psi)^{-1/2} \) y\( \tan\Psi =\frac{dy}{dx} \). La sustitución de estos en Ecuación\(\ref{eq:1.9.6}\) da la ecuación diferencial a la ruta en\((x , y)\) coordenadas:

\[ \left(\frac{dy}{dx}\right)^2 = \frac{(k-y)^2 -l^2}{l^2}, \quad \text{where} \quad l = k\cos\alpha. \label{eq:1.9.10} \]

Esto se puede integrar fácilmente para dar la\((x ,y)\) ecuación a la ruta:

\[ x = l\ln\left[\frac{k(1+\sin\alpha)}{k-y\pm\sqrt{(k-y)^2-l^2}}\right]. \label{eq:1.9.11} \]

En la Figura I.25 he tomado\(a = 1\) (es decir, estoy expresando todas las distancias en unidades de\(a\)), y estoy tomando\(n_0 = 1.5\) (de ahí\(k = 3\)), y calculo las trayectorias para\(\alpha\) = 15°, 30°, 45°, 60°, 75°.

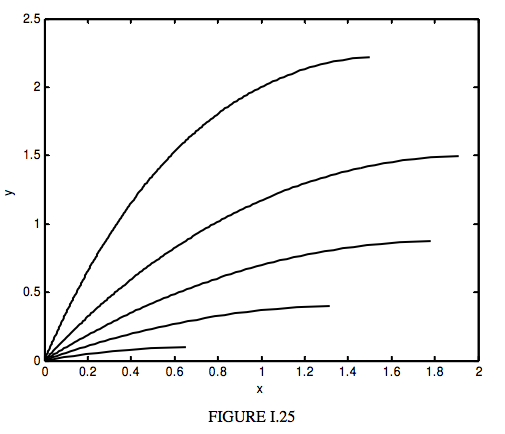
La Figura I.25 y la Ecuación\(\ref{eq:1.9.11}\) muestran las trayectorias de la luz si el índice de refracción varía de\(n_0\) at\(y = 0\), a 1 at\(y = a\) como se describe en la Ecuación\(\ref{eq:1.9.3}\). Pero ahora supongamos que el índice de refracción está variando con la altura según

\[ n = \frac{n_0a}{(n_0-1)y+a}.\label{eq:1.9.12} \]

En este modelo, también, el índice de refracción va de\(n_0\) at\(y = 0\), a 1 at\(y = a\), pero la variación no es lineal. De hecho te puede interesar convencerte de que es la velocidad de la luz la que va aumentando linealmente de\(y = 0\) a\(y = a\). A ver si se pueden trazar los caminos de los rayos de luz en esta situación. Creo que son arcos de círculos, y podrías ser capaz de calcular los radios y las coordenadas de los centros de los círculos. Aquí hay otro:

\[ n = \sqrt{\frac{n^2_0a}{(n^2_0-1)y+a}}. \label{eq:1.9.13} \]

Aquí, también, el índice de refracción va de\(n_0\) at\(y = 0\), a 1 at\(y = a\). Tal vez quieras intentar trazar los rayos en este modelo. Creo que pueden ser arcos de cicloides. Por supuesto que estos ejemplos pueden parecer muy improbables. ¿Te imaginas un bloque de vidrio de ancho\(a\), hecho de vidrio cuyo índice de refracción varía continuamente de 1.5 en un borde a cero en el otro? No muy probable, sin embargo hay una situación que viene a la mente en la que existe una variación continua del índice de refracción de algún valor basal\(n_0\) a cero. Estoy pensando en la atmósfera de la Tierra (o de hecho la atmósfera de cualquier planeta). A medida que la luz de una estrella viaja a través de la atmósfera terrestre, no se mueve en línea recta, sino en una ligera curva, de manera que se desvía a través de unos pocos minutos de arco antes de que llegue al telescopio del astrónomo. Para una estrella en la parte baja cerca del horizonte, la refracción asciende a casi medio grado. Esto debe tenerse en cuenta cuando los astrónomos están haciendo mediciones posicionales precisas. Y las ondas sonoras, que pasan por la atmósfera, también están sujetas a refracción a través de la forma diferencial de la ley de Snell. La velocidad del sonido (y de ahí el índice de refracción) varía con la temperatura de la atmósfera, y por lo tanto con la altura en la atmósfera. Entre las muchas aplicaciones de este tipo de teoría se encuentra la trayectoria de las ondas sonoras de los meteoritos que se precipitan a través de la atmósfera. Esto se discute en un artículo publicado en Meteoritics and Planetary Science 34, 572-585 (1999).