5.3.2: Fórmulas de FRESNEL
- Page ID
- 51139
El coeficiente de reflexión perpendicular \(r_{\perp}\) es la magnitud que liga \(R_{\perp}\) con \(A_{\perp}\). En concreto,
\[
\begin{aligned}
R_{\perp} &=\frac{n \cos \theta-n^{\prime} \cos \theta^{\prime}}{n \cos \theta+n^{\prime} \cos \theta} A_{\perp} \\
&=\frac{\sin \left(\theta^{\prime}-\theta\right)}{\sin \left(\theta^{\prime}+\theta\right)} A_{\perp} \\
&=\frac{k_{z}-k_{z}^{\prime}}{k_{z}+k_{z}^{\prime}} A_{\perp} \\
&=r_{\perp} A_{\perp}
\end{aligned}
\]
la definición del coeficiente de transmisión perpendicular, \(t_{\perp}\), es como sigue
\[
\begin{aligned}
T_{\perp} &=\frac{2 n \cos \theta}{n \cos \theta+n^{\prime} \cos \theta^{\prime}} A_{\perp} \\
&=\frac{2 \cos \theta \sin \theta^{\prime}}{\sin \left(\theta+\theta^{\prime}\right)} A_{\perp} \\
&=\frac{2 k_{z}}{k_{z}+k_{z}^{\prime}} A_{\perp} \\
&=t_{\perp} A_{\perp}
\end{aligned}
\]
Para las magnitudes según la dirección paralela
\[
\begin{aligned}
R_{\|} &=\frac{n^{\prime} \cos \theta-n \cos \theta^{\prime}}{n^{\prime} \cos \theta+n \cos \theta} A_{\|} \\
&=\frac{\tan \left(\theta-\theta^{\prime}\right)}{\tan \left(\theta+\theta^{\prime}\right)} A_{\|} \\
&=\frac{n^{\prime 2} k_{z}-n^{2} k_{z}^{\prime}}{n^{\prime 2} k_{z}+n^{2} k_{z}^{\prime}} A_{\|} \\
&=r_{\|} A_{\|}
\end{aligned}
\]
\(y\)
\[
\begin{aligned}
T_{\|} &=\frac{2 n \cos \theta}{n^{\prime} \cos \theta+n \cos \theta^{\prime}} A_{\|} \\
&=\frac{2 \sin \theta^{\prime} \cos \theta}{\sin \left(\theta+\theta^{\prime}\right) \cos \left(\theta-\theta^{\prime}\right)} A_{\mid} \\
&=\frac{2 n n^{\prime} k_{z}}{n^{\prime 2} k_{z}+n^{2} k_{z}^{\prime}} A_{\|} \\
&=t_{\|} A_{\|}
\end{aligned}
\]
No hay que memorizar estas relaciones (fórmulas de FRESNEL) pero sí qué operaciones llevan a ellas y las conclusiones que permiten establecer. Vamos a estudiar los diferentes casos que pueden presentarse.
Incidencia normal
En incidencia normal \(\theta=0\) y \(\theta^{\prime}=0\) y los coeficientes valen
\[
\begin{aligned}
r_{\perp} &=\frac{n-n^{\prime}}{n+n^{\prime}} \\
r_{\|} &=\frac{n^{\prime}-n}{n+n^{\prime}} \\
t_{\perp} &=\frac{2 n}{n+n^{\prime}} \\
t_{\|} &=\frac{2 n}{n+n^{\prime}}
\end{aligned}
\]
se puede observar que \(r_{\|}=-r_{\perp}\) y que \(t_{\|}=t_{\perp}\). En la incidencia normal el plano de incidencia no está definido (el vector de ondas y el normal a la interfase coinciden en dirección) y las ecuaciones responden diciendo que no hay dirección privilegiada, lo que se refleja en los coeficientes de transmisión. El signo negativo de los coeficientes de reflexión depende de la forma de escoger el sistema de referencia (paralelo, perpendicular). Un dato: si \(n=1\) y \(n^{\prime}=1.5\) en incidencia normal se tiene
\[
\begin{aligned}
r_{\|} &=-r_{\perp}=0.2 \\
t_{\|} &=t_{\perp}=0.8
\end{aligned}
\]
Caso \(n^{\prime}>n\) de la incidencia oblicua, ángulo de Brewster
En este caso los coeficientes de reflexión y transmisión en función del ángulo de incidencia tienen el aspecto de la figura 5.6. El comportamiento complementario de los coeficientes de reflexión y transmisión es justificable en virtud de la conservación de la energía, y comprobable observando a través de un vidrio un objeto adyacente a nosotros y otro al otro lado, en los dos casos de la figura \(5.7\) (incidencia normal y rasante). Dicho de otro modo, un vidrio normal se puede utilizar como un espejo perfecto en incidencias próximas a la rasante (aunque es impráctico).



Hay un coeficiente cuyo valor pasa por cero para cierto ángulo, que denominaremos ángulo de BREWSTER y denotaremos \(\theta_{B}\). Es el ángulo para el que \(r_{\|}\left(\theta_{B}\right)=0\). Si retornamos a la expresión de \(r_{\|}\)obtenemos la siguiente condición para \(\theta_{B}\)
\[
n^{\prime} \cos \theta_{B}=n \cos \theta_{B}^{\prime} \notag
\]
que debe verificarse junto con la ley de SNeLL. Si imponemos el cumplimiento de ambas obtenemos
\[
\tan \theta_{B}=\frac{n^{\prime}}{n} \notag
\]
Si \(r_{\|}=0\) entonces \(R_{\|}=0\), de modo que en ángulo de BREWSTER la luz reflejada siempre tiene polarización rectilínea y completamente perpendicular al plano de incidencia, independientemente del estado de polarización de la luz incidente. Tenemos, por lo tanto, un método para construir luz rectilíneamente polarizada incluso a partir de luz natural. Por otra parte, la determinación del ángulo de BREWSTER equivale a la determinación de un índice de refracción conocido el otro.
En general, cuando \(n^{\prime}>n\) los coeficientes de reflexión o transmisión son números reales, de modo que el desfase sólo puede ser de 0 o \(\pi\). Como consecuencia, si la luz incide con polarización rectilínea, se transmite o se refleja con polarización rectilínea. Pero el acimut de la luz transmitida o reflejada será, en general, distinto del de la luz incidente, en virtud de las relaciones entre coeficientes perpendicular y paralelo. El cambio de acimut depende de los índices de refracción involucrados, por lo que se puede utilizar para diseñar dispositivos para la medida del índice de refracción.
Caso \(n^{\prime}<n\) de incidencia oblicua, reflexión total
En este caso los coeficientes de reflexión se hacen 1 antes de la incidencia rasante (para \(\left.\theta=\theta_{C}\right) . \theta_{C}\) se llama ángulo crítico y se cumple \(n \sin \theta_{C}=n^{\prime}\)
El problema es que para \(\theta>\theta_{C}\) no podemos conocer \(\theta^{\prime}\) y por lo tanto no podemos calcular los coeficientes de reflexión y transmisión con ayuda de las fórmulas de FRESNEL. Ya que se llama reflexión total al fenómeno, ¿se cumple \(\mathbf{T}=0 ?\). Las ecM y sus condiciones de frontera dicen que no, puesto que debería ser además de \(\mathbf{T}=0, \mathbf{R}=\mathbf{A}=0\) y eso significa que no hay ondas por ningún lado.
Debemos retornar al planteamiento matemático del problema. Interpretemos la reflexión total desde el punto de vista de los vectores de onda; para \(\theta>\theta_{C}\)
\[
k_{x}^{\prime}=k_{x}=\frac{\omega}{c} n \sin \theta>n^{\prime} \frac{\omega}{c} \notag
\]

es decir, que una componente del vector de ondas tiene que ser mayor que su módulo. Esto sólo lo podemos abordar incrementando el módulo, es decir, adoptando un vector de ondas complejo.
\[
\begin{aligned}
\mathbf{k}_{c}^{\prime} &=\mathbf{k}^{\prime}+i \mathbf{a}^{\prime} \\
\mathbf{k}^{\prime 2}-\mathbf{a}^{\prime 2} &=n^{\prime 2} \frac{\omega^{2}}{c^{2}}
\end{aligned}
\]
Las ondas transmitidas y reflejadas no son superposición de ondas armónicas con vector de ondas real, sino complejo. Y las condiciones de frontera nos darán los valores de parte real y la imaginaria. Las ondas serán armónicas "planas", con el sentido de "planas" que ya ha sido explicado y que aparece cuando el vector de ondas es complejo (ondas planas inhomogéneas). Matemáticamente para la onda transmitida y reflejada respectivamente:
\[
\begin{aligned}
&\mathbf{E}_{t}=\mathbf{T} e^{i\left(\mathbf{k}_{c}^{\prime} \cdot \mathbf{r}-\omega^{\prime} t\right)}+\ldots \\
&\mathbf{E}_{r}=\mathbf{R} e^{i\left(\mathbf{k}_{c}^{\prime \prime} \cdot \mathbf{r}-\omega^{\prime \prime} t\right)}+\ldots
\end{aligned}
\]
Hay que reconstruir toda la solución del problema, para lo que vamos a dar los principales pasos. Se llevan estas dos expresiones a las condiciones de frontera donde el \(\mathbf{k}_{c}^{\prime}\) por ejemplo se determina a partir de la igualdad de las exponenciales sobre la superficie de discontinuidad (como antes). En \(z=0\) se tiene
\[
\mathbf{k}_{c}^{\prime} \cdot \mathbf{r}=\mathbf{k} \cdot \mathbf{r} \notag
\]
con lo que \(k_{x}=k_{c x}^{\prime}\) y \(k_{y}=k_{c y}^{\prime}\) (componentes tangenciales continuas). El plano de incidencia es \(x z\). Por la elección de ejes \(k_{c y}=0\) (el vector de ondas está en el plano \(x z\) ).
\[
k_{y}^{\prime}+i a_{y}^{\prime}=0 \notag
\]
que vale por dos ecuaciones
\[
\begin{aligned}
&k_{y}^{\prime}=0 \\
&a_{y}^{\prime}=0
\end{aligned}
\]
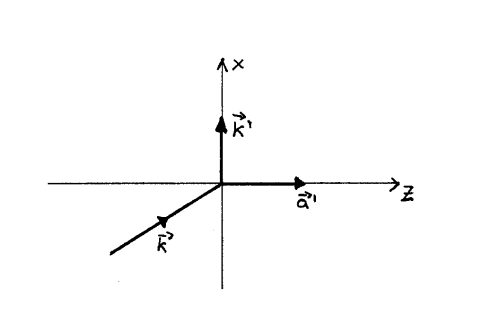
de modo que se puede decir que \(k^{\prime}, a^{\prime}\) están en el plano de incidencia. En lo que toca a \(k_{c x}\)
\[
k_{x}^{\prime}+i a_{x}^{\prime}=n \frac{\omega}{c} \sin \theta \notag \]
de donde
\[
\begin{aligned}
&a_{x}^{\prime}=0 \\
&k_{x}^{\prime}=n \frac{\omega}{c} \sin \theta
\end{aligned}
\]
Ya no podemos obtener más información de las condiciones de frontera. Además de esto sabemos que, por las ecMm, se ha de verificar
\[
\mathbf{k}_{c}^{\prime 2}=n_{c}^{\prime 2} \frac{\omega^{2}}{c^{2}}=n^{\prime 2} \frac{\omega^{2}}{c^{2}} \notag \]
de donde
\[
\begin{aligned}
\mathbf{k}^{\prime 2}-\mathbf{a}^{\prime 2} &=n^{\prime 2} \frac{\omega^{2}}{c^{2}} \\
\mathbf{k}^{\prime} \cdot \mathbf{a}^{\prime} &=0
\end{aligned}
\]
\(\mathbf{a}^{\prime}=0\) es solución, pero no nos sirve para la reflexión total. Pero á sólo puede tener componente \(z\) y \(\mathbf{k}^{\prime}\) sólo puede tener componente \(x\) (se deriva de las condiciones)
\[
\begin{aligned}
&\mathbf{a}^{\prime}=a_{z}^{\prime} \mathbf{u}_{z} \\
&\mathbf{k}^{\prime}=k_{x}^{\prime}=n \frac{\omega}{c} \sin \theta \mathbf{u}_{x}
\end{aligned}
\]
de donde \(a_{z}^{\prime}=\frac{\omega}{c} \sqrt{n^{2} \sin ^{2} \theta-n^{\prime 2}}\). La expresión para la onda transmitida queda
\[
\mathbf{E}_{t}=\mathbf{T} e^{-a_{z}^{\prime} z} e^{i(k x-\omega t)} \notag \]
Conclusiones de los resultados obtenidos para el caso de reflexión total:
- Hay onda transmitida ya que \(\mathbf{E}_{t} \neq 0\) del otro lado de la discontinuidad de índice: es una onda plana inhomogénea que vive pegada a la discontinuidad (onda evanescente), porque se atenúa exponencialmente con la distancia y no sobrevive más allá de unas pocas longitudes de onda. Si calculáramos la media del vector de POYNTING obtendríamos que la fase y la energía se propagan por la superficie de discontinuidad.
\[
\left\langle\mathbf{S}^{\prime}\right\rangle_{z}=0 \notag
\]
(no hay ningún flujo de energía ortogonal a la interfase).
- Tenemos la dependencia espaciotemporal de la onda ¿qué hay de la amplitud T?. Ahora tenemos una "ortogonalidad": se verifica \(\mathbf{k}_{c}^{\prime} \cdot \mathbf{T}=0\), pero no podemos aprovechar esto para decir que \(\mathbf{T} \perp \mathbf{k}^{\prime}\), ya que \(\mathbf{T}\) será en general un vector complejo. En general habría que aprovechar la condición expuesta en la forma \(\left(\mathbf{k}^{\prime}+i \mathbf{a}^{\prime}\right) \cdot \mathbf{T}=0\), pero no lo vamos a hacer. Escribiremos directamente la solución (fórmulas de FRESNEL).
\[
\begin{aligned}
r_{\perp} &=\frac{k_{z}-k_{c z}^{\prime}}{k_{z}+k_{c z}^{\prime}} \\
t_{\perp} &=\frac{2 k_{z}}{k_{z}+k_{c z}^{\prime}} \\
r_{\|} &=\frac{k_{z} n^{\prime 2}-k_{c z}^{\prime} n^{2}}{k_{z} n^{\prime 2}+k_{c z}^{\prime} n^{2}}
\end{aligned}
\]
su estructura es similar en \(\operatorname{los}\) casos \(r_{\perp}, t_{\perp}, r_{\|}\), pero poniendo el subíndice \(c\) a las componentes de la onda transmitida. Sin embargo \(t_{\|}\)se escribe en función de los campos magnéticos (a diferencia de los otros 3 ) y su escritura sí varía:
\[
t_{\|}=\frac{H_{\perp t}}{H_{\perp i}}=\frac{2 n^{\prime 2} k_{z}}{n^{\prime 2} k_{z}+n^{2} k_{c z}^{\prime}} \notag
\]
los detalles de este cálculo se encuentran en [Cabrera]. Utilizaremos principalmente las relaciones para los coeficientes de reflexión.
- Los coeficientes de reflexión son complejos, ya que \(k_{c z}^{\prime}\) es complejo:
\[
k_{z}=n \frac{\omega}{c} \cos \theta \notag
\]
\[
k_{c z}^{\prime}=i \frac{\omega}{c} \sqrt{n^{2} \sin ^{2} \theta-n^{\prime 2}} \notag
\]
Las cosas quedan
\[
r_{\perp}=\frac{n \cos \theta-i \sqrt{n^{2} \sin ^{2} \theta-n^{\prime 2}}}{n \cos \theta+i \sqrt{n^{2} \sin ^{2} \theta-n^{\prime 2}}} \notag
\]
como el numerador y el denominador son complejos conjugados se cumple la importante relación
\[
\left|r_{\perp}\right|=\left|r_{\|}\right|=1 \notag
\]
lo que permite escribirlos como \({ }^{1}\)
\[
\begin{aligned}
r_{\|} &=e^{i \delta_{\|}} \\
r_{\perp} &=e^{i \delta_{\perp}}
\end{aligned}
\]
\(\operatorname{con} \delta_{\|} \mathrm{y} \delta_{\perp}\) por determinar
\[
r_{\perp}=\frac{e^{i \frac{\delta_{\perp}}{2}}}{e^{-i \frac{\delta_{\perp}}{2}}}=\frac{\cos \frac{\delta_{\perp}}{2}+i \sin \frac{\delta_{\perp}}{2}}{\cos \frac{\delta_{\perp}}{2}-i \sin \frac{\delta_{\perp}}{2}} \notag
\]
lo que nos permite obtener la tangente
\[
\tan \frac{\delta_{\perp}}{2}=-\frac{\sqrt{\sin ^{2} \theta-\left(\frac{n^{\prime}}{n}\right)^{2}}}{\cos \theta} \notag
\]
pero lo que verdaderamente nos será útil es
\[
\tan \left(\frac{\delta_{\perp}-\delta_{\|}}{2}\right)=\frac{\cos \theta \sqrt{\sin ^{2} \theta-\left(\frac{n^{\prime}}{n}\right)^{2}}}{\sin ^{2} \theta} \notag
\]
- Lo importante: números complejos de módulo unidad y cambio del estado de polarización: la luz con polarización rectilínea se convertirá en general en elípticamente polarizada, dependiendo de la diferencia de fases de la fórmula anterior (por eso la hemos deducido).
- Ya tenemos modos de obtener las polarizaciones que queramos: la incidencia en ángulo de BREWSTER nos da polarización rectilínea, la reflexión y transmisión normales nos dan cambios de acimut dentro de la polarización rectilínea y la reflexión total nos da polarización elíptica. Sin embargo, encontraremos métodos más cómodos para obtener el estado de polarización que se desee en el desarrollo posterior de la asignatura.
______________________________________________________________________
1. atención en la bibliografía al convenio de signos en la exponencial compleja: las fórmulas posteriores dependen de ese convenio.

