11.1: Resueltos

Problema \(\PageIndex{1}\)

Consideremos el campo eléctrico

\[
\mathbf{E}(z, t)=E_{0} \cos (\omega t-k z) \mathbf{u}_{x}+E_{0} \sin (\omega t-k z) \mathbf{u}_{y} \notag
\notag \]

siendo \(\mathbf{u}_{x}, \mathbf{u}_{y}\) los correspondientes vectores unitarios. ¿Es una onda armónica?. Escribir \(\mathbf{E}\) en representación compleja. ¿Es una onda plana? ¿Cuál es su estado de polarización?

Respuesta

Sí es una onda armónica, pues se puede escribir del siguiente modo

\[
\begin{aligned}
\mathbf{E}(z, t) &=E_{0}\left(\mathbf{u}_{x}, \mathbf{u}_{y}\right)\left(\begin{array}{c}
\cos (\omega t-k z) \\
\sin (\omega t-k z)
\end{array}\right) \\
&=E_{0}\left(\mathbf{u}_{x}, \mathbf{u}_{y}\right)\left(\begin{array}{c}
\cos (\omega t-k z) \\
\cos \left(\omega t-k z-\frac{\pi}{2}\right)
\end{array}\right) \\
&=E_{0}\left(\mathbf{u}_{x}, i \mathbf{u}_{y}\right)\left(\begin{array}{c}
e^{i(\omega t-k z)} \\
e^{i(\omega t-k z)}
\end{array}\right) \\
&=\left(E_{0} \mathbf{u}_{x}+E_{0} i \mathbf{u}_{y}\right) e^{i(\omega t-k z)}
\end{aligned}
\notag \]

 

Problema \(\PageIndex{2}\)

Dar respuesta a las siguientes cuestiones

1. La suma de dos ondas planas ¿es siempre una onda plana?

2. ¿La superposición de dos ondas linealmente polarizadas iestá siempre linealmente polarizada?

3. La superposición de dos ondas circularmente polarizadas ¿̇está siempre circularmente polarizada?

Respuesta

1. Una onda armónica es aquella para la cual

\[
\frac{\partial^{2} \mathbf{E}}{\partial t^{2}}=-\omega^{2} \mathbf{E} \notag
\]

lo que es equivalente a la definición que hemos dado

\[
E_{j}=A_{j}(\mathbf{r}) \cos \left(\omega t-g_{j}(\mathbf{r})\right) \notag
\]

Se verifica que la dependencia temporal es armónica, lo cual no quiere decir que forzosamente la función dada sea una onda, es decir, cumpla la ecuación de ondas.

2. Representación compleja

\[
\mathbf{E}=\mathbf{E}_{0} \cos \left[\frac{k}{2} \mathbf{r} \cdot\left(\mathbf{u}_{1}+\mathbf{u}_{2}\right)\right] e^{i\left[\frac{k}{2} \mathbf{r} \cdot\left(\mathbf{u}_{1}+\mathbf{u}_{2}\right)-\omega t\right]} \notag
\notag \]

Nótese que cambiar el signo del argumento de la exponencial no cambia nada en la representación real, pues el coseno es una función par. Sólo hay que pasar a representación compleja el coseno que lleva la dependencia temporal. Lo que puede ser muy útil, y además es legítimo es reescribir el coseno que no depende del tiempo usando la fórmula

\[
\cos a=\frac{e^{i a}+e^{-i a}}{2} \notag
\notag \]

Observación: si utilizamos una fórmula trigonométrica para descomponer el producto de cosenos obtenemos una suma de dos ondas armónicas. Se deja como ejercicio para el lector.

3. Velocidad de fase. Los frentes de onda corresponden a los puntos que verifican

\[
\omega t-\frac{k}{2} \cdot \mathbf{r}\left(\mathbf{u}_{1}+\mathbf{u}_{2}\right)=c t e
\notag \]

para simplificar supongamos que la suma \(\mathbf{u}_{1}+\mathbf{u}_{2}\) sigue el eje \(z\left(\mathbf{u}_{1}+\mathbf{u}_{2}=\left|\mathbf{u}_{1}+\mathbf{u}_{2}\right| \mathbf{u}_{z}\right)\). Entonces

\[
\omega t-\frac{k}{2} z\left|\mathbf{u}_{1}+\mathbf{u}_{2}\right|=c t e
\notag \]

es decir, planos perpendiculares al eje \(z\). La velocidad de fase es el coeficiente que multiplica al tiempo en

\[
\begin{aligned}
z &=\frac{2 \omega}{k\left|\mathbf{u}_{1}+\mathbf{u}_{2}\right|} t-2 \frac{c t e}{k\left|\mathbf{u}_{1}+\mathbf{u}_{2}\right|} \\
&=v_{f} t-2 \frac{c t e}{k\left|\mathbf{u}_{1}+\mathbf{u}_{2}\right|}
\end{aligned}
\notag \]

Lo único que podemos decir es que será menor que la velocidad de la luz en el vacío. Para dar más precisiones necesitaríamos conocer \(\mathbf{u}_{1}\) y \(\mathbf{u}_{2}\).

4. Expresarlo como superposición de oap

\[
\mathbf{E}=\sum \mathbf{E}_{0 j} e^{i\left(\mathbf{k}_{j} \cdot \mathbf{r}-\omega_{j} t\right)}
\notag\]

para hacerlo no hay más que recordar la expresión del coseno que no depende del tiempo en función de exponenciales complejas. Manipulando un poco la representación compleja se obtiene, pues,

\[
\mathbf{E}=\frac{\mathbf{E}_{0}}{2} e^{i\left(k \mathbf{u}_{1} \cdot \mathbf{r}-\omega t\right)}+\frac{\mathbf{E}_{0}}{2} e^{i\left(k \mathbf{u}_{2} \cdot \mathbf{r}-\omega t\right)}
\notag \]

donde \(\mathbf{k}_{1}=k \mathbf{u}_{1} \mathrm{y} \mathbf{k}_{2}=k \mathbf{u}_{2} \mathrm{y} \omega_{1}=\omega_{2}=\omega\). Ahora podemos responder a la pregunta de si el campo dado es una oem: lo es en la medida en que se descompone en suma de oap, que son soluciones cada una de ellas por separado (siempre que \(|\mathbf{k}|=\frac{\omega}{c}\) ) y la ecO es lineal (la suma de soluciones es solución).

Problema \(\PageIndex{3}\)

Para cierta onda armónica plana

\[
\mathbf{E}(z, t)=\mathbf{E}_{0} e^{i(k z-\omega t)}
\notag \]

se tiene

\[
\mathbf{E}_{0}=\left(\begin{array}{l}
p+i q \\
f+i g
\end{array}\right)
\notag \]

1. \(f=2 p, g=2 q\).

2. \(f=q=0, p=g\)

3. \(p=0, q=0\)

Respuesta

1. \(f=2 p, g=2 q\). Esto implica

\[
\mathbf{E}_{0}=(p+i q)\left(\begin{array}{l} \notag
1 \\
2
\end{array}\right)
\notag \]

luz linealmente polarizada: \(\delta y-\delta x=0\). En representación real \(p+i q=e^{i \varphi}\) y se tiene

\[
\begin{aligned}
&E_{x}=a \cos (\omega t-k z-\varphi) \\
&E_{y}=2 a \cos (\omega t-k z-\varphi)
\end{aligned}
\notag \]

de donde se obtiene la polarización exactamente: es la recta

\[
E_{y}=2 E_{x}
\notag \]

2. \(f=2 p, g=2 q\) (hacer). Este segundo caso da circular levógira y en representación real, las ecuaciones paramétricas de una circunferencia

\[
\begin{aligned}
&E_{x}=p \cos (\omega t-k z) \\
&E_{y}=p \sin (\omega t-k z)
\end{aligned}
\notag \]

3. \(\operatorname{con} p=0, q=0\)

\[
\mathbf{E}_{0}=(f+i g)\left(\begin{array}{l}
0 \\
1
\end{array}\right)
\notag \]

de nuevo luz linealmente polarizada, vibrando en el eje \(y\).

Problema \(\PageIndex{4}\)

Estimar la amplitud del campo eléctrico de una oap cuyo promedio temporal del vector de POYNTING es

1. \(125 \mathrm{~W} / \mathrm{m}^{2}\) (bombilla)
a) \(1 \mathrm{~kW} / \mathrm{m}^{2}\) (luz solar).
b) \(1 \mathrm{~W} / \mathrm{cm}^{2}\) (láser continuo \(\left.\mathrm{He}-\mathrm{Ne}\right)\).
c) \(1 \mathrm{MW} / \mathrm{cm}^{2}\) (láser pulsado).

Respuesta

No hay más remedio que hacer una hipótesis: que las ondas son expresables como oaps. Y esto es totalmente falso en la mayoría de los casos.

\[
\mathbf{E}=\mathbf{E}_{0} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}
\notag \]

Sabemos que

\[
|\langle\mathbf{S}\rangle|=\frac{1}{2} \sqrt{\frac{\epsilon_{0}}{\mu_{0}}}\left|\mathbf{E}_{0}\right|^{2}
\notag \]

de donde

\[
\left|\mathbf{E}_{0}\right|=\sqrt{2 \sqrt{\frac{\epsilon_{0}}{\mu_{0}}}|\langle\mathbf{S}\rangle|}
\notag \]

los valores numéricos que se obtienen son \(307 \frac{\mathrm{V}}{\mathrm{m}}, 868 \frac{\mathrm{V}}{\mathrm{m}}, 2.7 \times 10^{3} \frac{\mathrm{V}}{\mathrm{m}}, 2.7 \times 10^{6} \frac{\mathrm{V}}{\mathrm{m}}\), respectivamente. Para comparar, el campo eléctrico que siente un electrón de un átomo de \(\mathrm{H}\) es, muy aproximadamente

\[
|\mathbf{E}|=\frac{1}{4 \pi \epsilon_{0}} \frac{1}{r^{2}} \approx 10^{11} \frac{V}{m}
\notag \]

podemos apreciar que los cem de las ondas son siempre muy pequeños comparados con los campos atómicos internos. Esto puede servir para justificar la aproximación lineal para la fuerza recuperadora que hemos adoptado en el desarrollo teórico.

Problema \(\PageIndex{5}\)

Consideremos dos ondas planas monocromáticas linealmente polarizadas que se propagan en la misma dirección. Determinar el promedio temporal del vector de \(\mathrm{POYN}-\) TING de la superposición de ambas ondas si las dos ondas tienen la misma frecuencia y los vectores \(\mathbf{E}\) perpendiculares.

Respuesta

Suponemos propagación en el eje \(z\), por lo que escribimos la proporcionalidad a un vector real como

\[
\begin{aligned}
&\mathbf{E}_{01} \propto \mathbf{u}_{x} \\
&\mathbf{E}_{02} \propto \mathbf{u}_{y}
\end{aligned}
\notag \]

La superposición de ambos campos es una oap de amplitud \(\left(\mathbf{E}_{01}+\mathbf{E}_{02}\right) e^{i(k z-\omega t)}\) de modo que, según la fórmula

\[
\langle\mathbf{S}\rangle=\frac{1}{2} \sqrt{\frac{\epsilon_{0}}{\mu_{0}}}\left|\mathbf{E}_{01}+\mathbf{E}_{02}\right|^{2} \mathbf{u}_{k}=\left(\left\langle\mathbf{S}_{1}\right\rangle+\left\langle\mathbf{S}_{2}\right\rangle\right)
\notag \]

Observaciones: para que esto ocurra basta con que los productos escalares \(\mathbf{E}_{01}^{*} \cdot \mathbf{E}_{02}\) y \(\mathbf{E}_{01} \cdot \mathbf{E}_{02}^{*}\) sean nulos. Los estados de polarización en que esto ocurre se llaman estados de polarización ortogonales. Pero esta condición además de las polarizaciones lineales ortogonales, la cumplen dos ondas polarizadas circularmente, una dextro y otra levo.

Para llegar a esto bastaría con haber considerado detenidamente la estructura de la onda y la definición del vector de POYNTING.

\[
\mathbf{S}=\frac{1}{\mu_{0}}\left(\mathbf{E}_{1}+\mathbf{E}_{2}\right) \wedge\left(\mathbf{B}_{1}+\mathbf{B}_{2}\right)=\mathbf{S}_{1}+\mathbf{S}_{2}
\notag \]

como la operación de promediado es lineal se llega a \(\langle\mathbf{S}\rangle=\left\langle\mathbf{S}_{1}\right\rangle+\left\langle\mathbf{S}_{2}\right\rangle\).

Problema \(\PageIndex{6}\)

Una carga ligada es iluminada por una onda armónica, plana y circularmente polarizada que se se propaga en la dirección \(Z\). Demostrar que \(\mathbf{r}(t)\) describe una circunferencia en el plano \(X Y\).

Respuesta

La ecuación de la trayectoria de una carga ligada es

\[
\mathbf{r}(t)=\frac{\frac{q}{m}}{\omega_{0}^{2}-\omega^{2}-i \gamma \omega} \mathbf{E}_{0} e^{-i \omega t}
\notag \]

Una oap que se propague en la dirección del eje \(z\) cumple

\[
\begin{aligned}
&\nabla \cdot \mathbf{E}=0 \\
&\mathbf{k} \cdot \mathbf{E}=0
\end{aligned}
\notag \]

de modo que la componente \(z\) del campo según el eje \(z\) es nula. Así sucederá con el vector \(\mathbf{r}(t)\), que es proporcional a él. De suerte que el movimiento de las cargas se produce en

Figure \(\PageIndex{1}\): El vector \(\mathbf{r}\) persigue al vector \(\mathbf{E}\)

el plano \(x y\). Es evidente que la trayectoria es circular, puesto que los dos vectores son proporcionales.

De otro modo,

\[
\mathbf{r}=\beta \mathbf{E}_{0} e^{-i \omega t}=|\beta| e^{i \delta} \mathbf{E}^{-i \omega t}=|\beta| \mathbf{E}_{0} e^{-i \omega\left(t-\frac{\delta}{\omega}\right)}
\notag \]

es decir, \(\mathbf{r}(t)=|\beta| \mathbf{E}\left(t-\frac{\delta}{\omega}\right)\). La trayectoria que sigue la separación entre cargas es la misma que la del campo eléctrico, solo que con un desfase temporal. Y esto se puede aplicar a cualquier estado de polarización.

P

Problema \(\PageIndex{7}\)

Demostrar que el promedio temporal de la potencia transferida a un electrón ligado \(P=\langle q \dot{\mathbf{r}} \cdot \mathbf{E}\rangle\) cuando es iluminado por una oap es

\[
P=\frac{q^{2}}{2 m} \frac{\gamma \omega^{2}}{\left(\omega^{2}-\omega_{0}^{2}\right)^{2}+\gamma^{2} \omega^{2}}\left|\mathbf{E}_{0}\right|^{2}
\notag \]

Evaluar esta expresión con los datos del problema anterior. Calcular el tamaño de una superficie sobre la que incide la misma potencia debido a la misma onda armónica plana.

Respuesta

1. No hay más que escribir explícitamente la expresión \(q \dot{\mathbf{r}} \cdot \mathbf{E} \mathrm{y}\) hacer su promedio temporal

\[
q \mathbf{r}=\alpha \mathbf{E}=\alpha \mathbf{E}_{0} e^{-i \omega t}
\notag \]

donde \(\alpha\) es la polarizabilidad. Como hemos separado la dependencia temporal

\[
q \dot{\mathbf{r}}=(-i \omega) \alpha \mathbf{E}_{0} e^{-i \omega t}
\notag \]

Como tenemos un producto de cosas, que no es una operación lineal, no podemos utilizar la representación compleja. De modo que vamos a pasar \(\dot{\mathbf{r}}\) y E a representación real. Pero eso ya lo hicimos para el vector de POYNTING, sólo que con un producto vectorial y no escalar. Revisando esos cálculos uno se convence de que

\[
\langle q \dot{\mathbf{r}} \cdot \mathbf{E}\rangle=\frac{1}{2} \Re\left\{q \dot{\mathbf{r}} \cdot \mathbf{E}^{*}\right\}
\notag \]

Aquí sí que vale la representación compleja

\[
q \dot{\mathbf{r}} \cdot \mathbf{E}^{*}=-i \omega \alpha\left|\mathbf{E}_{0}\right|^{2}
\notag \]

de donde

\[
P=-\frac{i \omega}{4}\left(\alpha-\alpha^{*}\right)\left|\mathbf{E}_{0}\right|^{2}
\notag \]

expresión de la que se sigue inmediatamente la conclusión. Ésta es la energía que la carga extrae de la onda incidente. Obsérvese que es proporcional a \(\gamma\).

2. Para \(\omega=5 \times 10^{15} \mathrm{rad} / \mathrm{s}\) la potencia extraída por la carga es \(4.34 \times 10^{-25} \mathrm{~W}\) mientras que para \(\omega_{0}\) es \(1.4 \times 10^{-10} W\) ¡una diferencia de quince órdenes de magnitud!. Cambios pequeños en frecuencia significan cambios enormes en la interacción radiación-materia. Toda la energía que extrae la carga es luego reemitida en forma de ondas electromagnéticas.

3. Es una forma de evaluar el tamaño efectivo del átomo, la sección transversal que absorbería la misma energía que la carga ligada. Esa superficie se llama sección eficaz. El \(\langle\mathbf{S}\rangle\) es potencia por unidad de superficie, de modo que (si la normal a la superficie coincide con el vector de POYNTING)

\[
|\langle\mathbf{S}\rangle| A=P
\notag \]

Como se trata de una oap, se cumple

\[
|\langle\mathbf{S}\rangle|=\frac{1}{2} \sqrt{\frac{\epsilon_{0}}{\mu_{0}}}\left|\mathbf{E}_{0}\right|^{2}
\notag \]

y no hay más que sustituir los datos en la expresión \(A=\frac{P}{|\langle\mathbf{S}\rangle|}\). Se encuentra, respectivamente, para \(\omega=5 \times 10^{15} \mathrm{rad} / \mathrm{s}\) la sección eficaz es de \(3.34 \times 10^{-28} \mathrm{~m}^{2}\) mientras que para \(\omega_{0}\) es \(1.08 \times 10^{-13} \mathrm{~m}^{2}\) ¡una diferencia de quince órdenes de magnitud!. Si suponemos la superficie circular, los radios respectivos son \(10^{-5} \mathrm{~nm}\) y \(185 n m\). Este segundo número es enorme. Esto es una signatura de que nuestros cálculos en la resonancia no son tan precisos como pensamos. El primer dato viene a ser una milésima del tamaño del átomo.

P

Problema \(\PageIndex{8}\)

(el cielo azul...) Si en el problema anterior \(\omega_{0}\) está en el ultravioleta, dígase si la potencia transferida es mayor para una \(\omega\) en el rojo o en el azul (considérese \(\left.\gamma \ll \omega \ll \omega_{0}\right)\).

Respuesta

Las aproximaciones que hacemos son \(\left(\omega^{2}-\omega_{0}^{2}\right)^{2}-\gamma^{2} \omega^{2} \approx \omega_{0}^{4}+\gamma^{2} \omega^{2} \approx \omega_{0}^{4}\)

\[
P \approx \frac{q^{2}}{2 m} \frac{\gamma \omega^{2}}{\omega_{0}^{4}}\left|\mathbf{E}_{0}\right|^{2}
\notag \]

como \(\omega_{A}>\omega_{R}\), se concluye que la carga es mucho más sensible a las ondas en el azul. Observaciones:

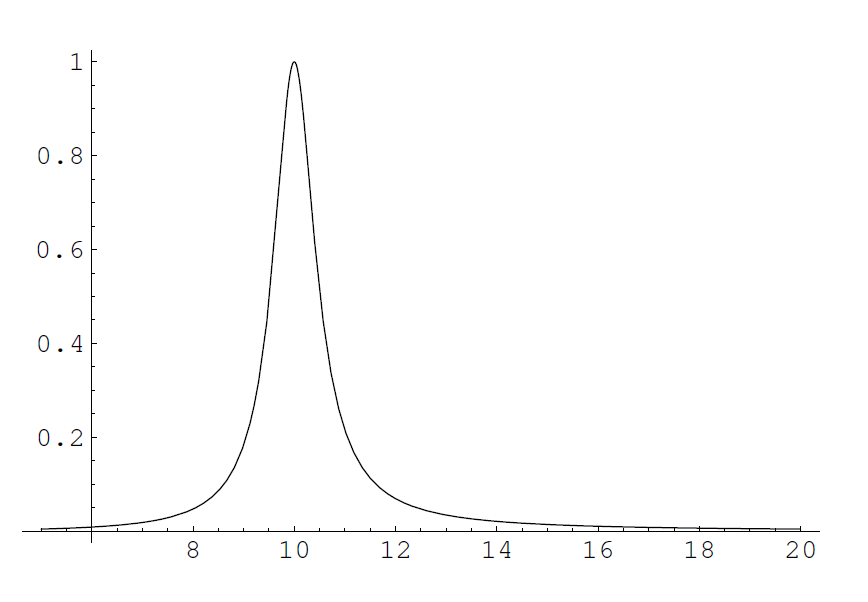
Figura \(\PageIndex{2}\): Aspecto cualitativo de la función \(P(\omega)\) con \(\omega_{0}=10\)

1. En la bibliografía encontraremos una dependencia no en \(\omega^{2}\) sino en \(\omega^{4}\), ya que se suelen tomar mejores aproximaciones de la dependencia con \(\dot{\mathbf{r}}\) de \(\gamma\).

2. Esta fórmula puede dar cuenta del color azul del cielo, así como de los tonos rojizos del atardecer. Las moléculas del aire extraen más azul que rojo de la luz blanca incidente. Y reemiten en azul, pero no en la dirección incidente, sino en todas direcciones. En el haz que progresa, por esto mismo, queda más rojo que azul.

Cuando por el día miramos a una dirección arbitraria del espacio (que no sea la del sol) la luz no puede venir más que de la dispersión de la luz solar por la atmósfera. En el crepúsculo ocurre el fenómeno complementario: cuando miramos al sol, que además atraviesa una gruesa capa atmosférica por ser casi tangencial, vemos las componentes cromáticas que quedan en el haz que progresa, es decir, mayoritariamente el rojo.

3. Este cálculo lo hemos hecho suponiendo que la atmósfera es un medio ópticamente no denso, lo que es falso. Pero nuestra suposición funciona porque en realidad existen fluctuaciones de densidad, bolsas de aire de mayor densidad que el entorno que se comportan como una especie de agregados que, ellos sí, constituyen un medio ópticamente poco denso para el que vale el tratamiento que se ha utilizado suponiendo unidades más pequeñas.

Problema \(\PageIndex{9}\)

Se tiene un dieléctrico que tiene una sola frecuencia de resonancia \(\omega_{0}=\) \(3.01 \times 10^{15} \mathrm{rad} / \mathrm{s}\). En dicho medio se propagan tres ondas de frecuencias

\[
\begin{aligned}
&\omega_{1}=3.04 \times 10^{15} \mathrm{rad} / \mathrm{s} \\
&\omega_{2}=3.14 \times 10^{15} \mathrm{rad} / \mathrm{s} \\
&\omega_{3}=3.02 \times 10^{15} \mathrm{rad} / \mathrm{s}
\end{aligned}
\notag \]

¿Cuál de ellas se atenuará más a medida que se propague? ¿Por qué?.Por sencillez considérese que para dichas ondas \(\mathbf{k} y\) a son paralelos.

Respuesta

Hay atenuación en tanto en cuanto hay absorción (si \(\kappa=0\) entonces \(\mathbf{a} \perp \mathbf{k}\) o bien \(\mathbf{a}=0\), y en el primer caso la onda no se atenúa a medida que se propaga tampoco: el promedio temporal del vector de POYNTING no decrece). Si imaginamos la situación \(\mathbf{k} \|\) a para las tres ondas \(\mathbf{a}=\frac{\omega}{c} \kappa \mathbf{u}_{a}\). Pero una vez que \(\kappa \neq 0\) (y eso ocurre para las tres frecuencias) estrictamente no se puede decir para qué \(\omega\) la atenuación es mayor. No obstante, si nos restringimos al caso particular expuesto, y teniendo en cuenta la representación \(\kappa(\omega)\), la solución es \(\omega_{3}\) (a depende no de \(\kappa\) sino de \(\kappa \omega\), pero eso no cambia la conclusión - monotonía de la función, todas las frecuencias al mismo lado del pico-).

P

Problema \(\PageIndex{10}\)

(ionosfera: transparente al visible, espejo en radiofrecuencia) En la ionosfera el número de electrones libres por metro cúbico es \(N \simeq 10^{11} \mathrm{~m}^{-3}\). Calcular su contribución a \(n\) y \(\kappa\) para frecuencias del visible suponiendo que \(\gamma\) es despreciable.

Respuesta

Con \(\gamma \simeq 0\) se tiene el índice

\[
n_{c}^{2}=1-N \frac{e^{2}}{m_{e} \epsilon_{0}} \frac{1}{\omega^{2}}=1-\frac{\omega_{p}^{2}}{\omega^{2}}
\notag \]

utilizando, como para el caso de los metales, la noción de frecuencia de plasma, \(\omega_{p}=\) \(e \sqrt{\frac{N}{m_{e} \epsilon_{0}}}\), que es un parámetro que agrupa todas las características intrínsecas del material. Una evaluación numérica para los electrones de la ionosfera arroja

\[
\begin{aligned}
\omega_{p} &=1.602 \times 10^{-19} C \sqrt{\frac{10^{11} \mathrm{~m}^{-3}}{9.1 \times 10^{-31} \mathrm{~kg} \times 8.85 \times 10^{-12} \frac{C^{2}}{N m^{2}}}} \\
& \simeq 1.76 \times 10^{7} \mathrm{~Hz}
\end{aligned}
\notag \]

que está muy por debajo de las frecuencias del visible (orden \(10^{15} H z\) ), lo que significa

\[
n_{c}^{2} \simeq 1
\notag \]

entonces \(n_{c} \simeq n\) y por lo tanto \(\kappa \simeq 0 .\) La ionosfera es transparente al visible, hecho concordante con la experiencia diaria. Por otra parte, el valor del índice \(n \simeq 1\) es también lo que cabía esperar. La ionosfera será completamente transparente para el visible, pero reflectora para las radiofrecuencias, lo que es utilizado para propagar las ondas de radio.

P

Problema \(\PageIndex{11}\)

El promedio del campo eléctrico sobre los átomos viene dado por \(\mathbf{E}+\frac{1}{3 \epsilon_{0}} \mathbf{P}\). Demuéstrese la siguente relación entre la constante dieléctrica relativa \(\epsilon_{r}=\frac{\epsilon}{\epsilon_{0}}\) y la polarizabilidad atómica \(\alpha\).

\[ \epsilon_{r}=\frac{1+\frac{2 N_{v} \alpha}{3 \epsilon_{0}}}{1-\frac{N_{v} \alpha}{3 \epsilon_{0}}}
\notag \]

Respuesta

Ligábamos la constante dieléctrica con la polarización a través del momento dipolar por unidad de volumen.

\[
\begin{aligned}
\mathbf{P} &=\chi_{e} \epsilon_{0} \mathbf{E}_{m a c} \\
\epsilon &=\epsilon_{0}\left(1+\chi_{e}\right) \\
\mathbf{P} &=\alpha \frac{N}{\Delta V} \frac{1}{N} \sum_{j \in \Delta V} \mathbf{E}_{j, m i c}
\end{aligned}
\notag \]

Vamos a considerar que el promedio del campo microscópico actuante sobre los átomos no es \(\mathbf{E}\) (como en el desarrollo de la teoría) sino \(\mathbf{E}+\frac{1}{3 \epsilon_{0}} \mathbf{P}\). Entonces

\[
\mathbf{P}=N_{V} \alpha\left(\mathbf{E}_{m a c}+\frac{1}{3 \epsilon_{0}} \mathbf{P}\right)
\notag \notag \notag \]

\(\operatorname{con} N_{V}=\frac{N}{\Delta V} \cdot\) Si despejamos

\[
\mathbf{P}=\frac{N_{V} \alpha}{1-\frac{N_{V} \alpha}{3 \epsilon_{0}}} \mathbf{E}_{m a c}
\notag \notag \notag \]

y la susceptibilidad es

\[
\chi_{e}=\frac{\frac{N_{V} \alpha}{\epsilon_{0}}}{1-\frac{N_{V} \alpha}{3 \epsilon_{0}}}
\notag \notag \notag \]

de donde se llega sin dificultad a la igualdad propuesta en el enunciado.

P

Problema \(\PageIndex{12}\)

Aproximese \(\epsilon_{r}\) en el problema anterior si \(\frac{N \alpha}{\epsilon_{0}} \ll 1\).

Respuesta

Lo que podemos hacer es desarrollar el denominador en sdp del término pequeño y quedarnos en la aproximación lineal.

\[
\begin{aligned}
\epsilon_{r} &=\frac{1+\frac{2 N_{V} \alpha}{3 \epsilon_{0}}}{1-\frac{N_{V} \alpha}{3 \epsilon_{0}}} \\
&=\left(1+\frac{2 N_{V} \alpha}{3 \epsilon_{0}}\right)\left(1+\frac{N_{V} \alpha}{3 \epsilon_{0}}+\ldots\right)
\end{aligned}
\notag \notag \notag \]

despreciando términos cuadráticos en \(\alpha\)

\[
\epsilon_{r} \simeq 1+\frac{2 N_{V} \alpha}{3 \epsilon_{0}}+\frac{N_{V} \alpha}{3 \epsilon_{0}}=1+\frac{N_{V} \alpha}{\epsilon_{0}}
\notag \notag \notag \]

\(11.1\) Resueltos

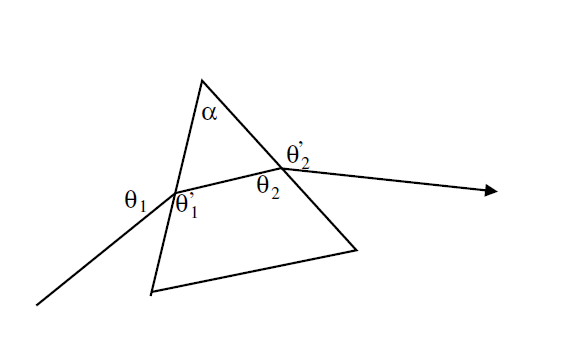
Figura \(\PageIndex{3}\): Un prisma de vidrio de ángulo \(\alpha\).

Esta expresión que hemos obtenido es la que hemos manejado en la teoría. Esta aproximación consiste en despreciar el término \(\frac{1}{3 \epsilon_{0}}\) en el promedio del campo actuante sobre los átomos. La condición de validez de la aproximación utilizada en teoría es, pues \(\frac{N \alpha}{\epsilon_{0}} \ll 1\).

Problema \(\PageIndex{13}\)

(prismas para desviar sin pérdidas) Considérese un haz plano linealmente polarizado que incide desde el aire sobre un prisma transparente de vidrio de ángulo \(\alpha\) (ver figura 11.3). Se desea que dicho haz atraviese el prisma sin sufrir pérdidas por reflexión en ninguna de las dos caras. ¿Cuánto deben valer

1. el acimut del haz incidente

2. el ángulo de incidencia

3. y el indice de refracción del prisma

para que tal cosa ocurra?

Respuesta

No queremos que haya luz reflejada en ninguna de las interfases, para que la atenuación sea mínima. En principio tenemos que calcular los coeficientes de reflexión y ver en qué circunstancias se anulan

\[
\begin{aligned}
R_{1 \|} &=r_{\|} A_{\|} \\
R_{1 \perp} &=r_{\perp} A_{\perp}
\end{aligned}
\notag \notag \notag \]

\(\mathbf{R}_{1}=0\) implica forzosamente \(A_{\perp}=0\) ya que \(r_{\perp}\) nunca se anula: el haz incidente debe tener sólo componente paralela (acimut cero). Por otra parte \(r_{\|}=0\) implica que la incidencia en la primera cara del prisma debe ser en ángulo de BREWSTER \(\theta_{1}=\theta_{B}\). Los resultados se pueden trasponer a la segunda cara: la incidencia debe ser allí también en ángulo de BREWSTER. Hace falta ver qué valen \(\theta_{1}(\alpha)\) y \(n_{v}(\alpha)\).

Con la condición de Brewster, la ley de SNELL, etc, escribimos:

\[
\begin{aligned}
\tan \theta_{1} &=n_{v} \\
\sin \theta_{1} &=n_{v} \sin \theta_{1}^{\prime} \\
n_{v} \cos \theta_{1} &=\cos \theta_{1}^{\prime} \\
\sin \theta_{1}^{\prime} &=\cos \theta_{1} \\
\theta_{1}^{\prime}+\theta_{1} &=\frac{\pi}{2} \\
\tan \theta^{\prime} &=n_{v} \\
\tan \theta_{2} &=\frac{1}{n_{v}} \\
\sin \theta_{2} &=n_{v} \sin \theta_{2}^{\prime} \\
n_{v} \cos \theta_{2} &=\cos \theta_{2}^{\prime} \\
\sin \theta_{2}^{\prime} &=\cos \theta_{2} \\
\theta_{2}^{\prime}+\theta_{2} &=\frac{\pi}{2}
\end{aligned}
\notag \notag \notag \]

de aquí se tiene \(\theta_{1}+\theta_{2}=\frac{\pi}{2}\); utilizando las tres relaciones entre ángulos se llega a la expresión, en la que aparece \(\alpha\)

\[
\begin{aligned}
\pi-\theta_{1}^{\prime}-\theta_{2}+\alpha &=\pi \\
\alpha &=\theta_{1}^{\prime}+\theta_{2}
\end{aligned}
\notag \notag \notag \]

si usamos el valor hallado para \(\alpha\) con \(\theta_{2}=\theta_{1}^{\prime}\) llegamos a \(\theta_{2}=\frac{\alpha}{2}\) o bien \(\theta_{1}=\frac{\pi}{2}-\frac{\alpha}{2}\). También

\[
n_{v}=\frac{1}{\tan \left(\frac{\alpha}{2}\right)}
\notag \notag \notag \]

Comentario: la trayectoria del rayo dentro del prisma es perpendicular a la bisectriz del ángulo, lo que coincide con la condición de desviación mínima. Por otra parte, la utilidad de un prisma como el que acabamos de describir es desviar un rayo sin pérdidas. Este método presenta ventajas frente a la utilización de espejos, siempre que seamos capaces de obtener medios perfectamente transparentes.

P

Problema \(\PageIndex{14}\)

Un haz de luz linealmente polarizado incide sobre un prisma isósceles de indice de refracción 1.5 tal y como se muestra en la figura 11.4. El campo eléctrico oscila en un plano que forma un ángulo con el plano de incidencia de \(45^{\circ}\). Se desea saber el tipo de polarización del haz saliente s y su intensidad respecto a la del haz incidente \(i\) en los casos en que el medio que rodea al prisma sea: a) aire ( \(n=1)\) b) agua \((n=1.33)\).

Respuesta

1. Planteamiento. Se tiene \(\left|A_{\|}\right|=\left|A_{\perp}\right|=\frac{1}{\sqrt{2}}|\mathbf{A}|\left(\right.\) el acimut es \(\left.\alpha=45^{\circ}\right)\). Para responder a las preguntas sobre el haz \(s\) (haz emergente) tenemos que poner en relación \(11.1\) Resueltos

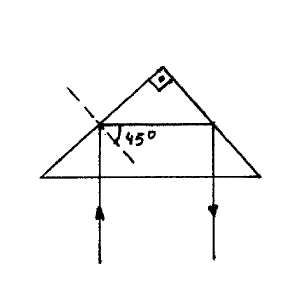
Figura \(\PageIndex{4}\): Prisma isósceles de \(n=1.5\).

las amplitudes, lo cual se hace con las fórmulas de FRESNEL. A los sucesivos procesos de transmisión-reflexión-reflexión-transmisión los denotaremos por \(1,2,3,4\) respectivamente.

\[
\begin{aligned}
A_{\|}^{\prime} &=t_{\|}^{(4)} r_{\|}^{(3)} r_{\|}^{(2)} t_{\|}^{(1)} A_{\|} \\
A_{\perp}^{\prime} &=t_{\perp}^{(4)} r_{\perp}^{(3)} r_{\perp}^{(2)} t_{\perp}^{(1)} A_{\perp}
\end{aligned}
\notag \notag \notag \]

Vamos a despreciar reflexiones múltiples: la onda se podría reflejar en 4 , recorrer el camino inverso, reflejarse de nuevo en 1 y volver para contribuir a la onda emergente. Habida cuenta de que \(n=1.5\) la contribución sería, en todo caso muy pequeña.

2. Cálculo. Una vez escritas las fórmulas anteriores sólo queda calcular. Las transmisiones 1,4 son en condiciones de incidencia normal \((\theta=0)\)

\[
\begin{aligned}
&t_{\|}^{(1)}=t_{\perp}^{(1)}=\frac{2 n_{a}}{n_{a}+n} \\
&t_{\|}^{(4)}=t_{\perp}^{(4)}=\frac{2 n}{n_{a}+n}
\end{aligned}
\notag \notag \notag \]

por simetría sabemos que \(r_{\|}^{(2)}=r_{\|}^{(3)}\) y \(r_{\perp}^{(3)}=r_{\perp}^{(3)}\). Consejo: cuando vayamos de mayor a menor índice es conveniente examinar si estamos en condiciones de reflexión total o no para escoger las expresiones adecuadas. Para saberlo calculamos \(n \sin 45^{\circ}=1.06 \mathrm{y}\) lo comparamos con \(n_{a}\).

- Si \(n_{a}=1\) estamos en reflexión total (vidrio-aire)

- Si \(n_{a}=1.33\) no hay reflexión total (existe \(\theta^{\prime}\) para el caso vidrio-agua).

Tenemos que separar el estudio de ambos casos. Comenzaremos por el caso más sencillo \(\left(n_{a}=1.33\right)\).

a) Podemos usar las fórmulas para los coeficientes de reflexión en las que aparecen los índices de ambos medios, el ángulo de incidencia y el ángulo de refracción (que hallamos por la ley de SNELL y vale \(\theta^{\prime}=0.92\) ).

\[
\begin{aligned}
r_{\|} &=0.01921 \\
r_{\perp} &=0.1386 \\
t_{\perp}^{(1)}=t_{\|}^{(1)} &=0.94 \\
t_{\perp}^{(4)}=t_{\|}^{(4)} &=1.06
\end{aligned}
\notag \]

el resultado es

\[
\begin{aligned}
A_{\|}^{\prime} &=3.7 \times 10^{-4} A_{\|}=2.6 \times 10^{-4}|\mathbf{A}| \\
A_{\|}^{\prime} &=1.9 \times 10^{-2} A_{\perp}=1.35 \times 10^{-2}|\mathbf{A}|
\end{aligned}
\notag \]

como \(\mathbf{A}^{\prime} \propto\) vector real la polarización es lineal. Podemos calcular su acimut, que vale

\[
\begin{aligned}
\tan \alpha^{\prime} &=\frac{A_{\perp}^{\prime}}{A_{\|^{\prime}}}=52 \\
\alpha^{\prime} &=89^{\circ}
\end{aligned}
\notag \]

El que los coeficientes de transmisión sean mayores que 1 no significa que la energía aumente en la transmisión. Como en la media del vector de POYNTING aparecen los índices hay casos en que un coeficiente es mayor que 1 y la energía, por supuesto se conserva. De hecho, cuando el cambio de medio se produce en el sentido de disminución de índice, como es el caso de este problema, se demuestra que los coeficientes de transmisión tienen que ser mayores que \(1 .\) Las que tienen que ser menores que la unidad son las transmitancias, ya que en su expresión intervienen los índices para compensar:

\[
\mathcal{T}_{\perp}=\frac{n^{\prime}}{n}\left|t_{\perp}\right|^{2}
\notag \]

Para responder a la segunda cuestión hace falta percatarse de que

\[
\frac{I^{\prime}}{I}=\frac{\left|\mathbf{A}^{\prime}\right|^{2}}{|\mathbf{A}|^{2}}=\frac{\left|\mathbf{A}_{\|}^{\prime}\right|^{2}+\left|\mathbf{A}_{\perp}^{\prime}\right|^{2}}{|\mathbf{A}|^{2}}=1.83 \times 10^{-4}
\notag \]

Apenas se refleja luz (menos de un \(0.02 \%)\).

b) Ahora tenemos que resolver el caso en que hay reflexión total \(\left(n_{a}=1\right)\).

\[
\begin{aligned}
r_{\|} &=e^{i \delta_{\|}} \\
r_{\perp} &=e^{i \delta_{\perp}}
\end{aligned}
\notag \]

si queremos saber el estado de polarización sólo nos interesa la diferencia de fase, por lo que usamos la expresión

\[
\tan \left(\frac{\delta_{\perp}-\delta_{\|}}{2}\right)=\frac{\cos \theta \sqrt{\sin ^{2} \theta-\left(\frac{n_{a}}{n}\right)^{2}}}{\sin ^{2} \theta}=\frac{1}{3}
\notag \notag \notag \]

de donde \(\delta_{\perp}-\delta_{\|}=0.32 \mathrm{rad}=18.4^{\circ} \mathrm{y}\)

\[
\begin{aligned}
&t_{\perp}^{(1)}=t_{\|}^{(1)}=0.8 \\
&t_{\perp}^{(4)}=t_{\|}^{(4)}=1.2
\end{aligned}
\notag \]

que conducen a las siguientes relaciones entre las amplitudes de entrada y la de salida

\[
\begin{aligned}
A_{\|}^{\prime} &=0.96 e^{i 2 \delta_{\|}} A_{\|}=0.679 e^{i 2 \delta \|}|\mathbf{A}| \\
A_{\perp}^{\prime} &=0.96 e^{i 2 \delta_{\perp}} A_{\perp}=0.679 e^{i 2 \delta_{\perp}}|\mathbf{A}| \\
& 2\left(\delta_{\perp}-\delta_{\|}\right)=1.287=73.7^{\circ}
\end{aligned}
\notag \]

No es lineal, y como la diferencia de fases no es \(\pm \frac{\pi}{2}\) tampoco tiene polarización circular, luego la polarización es elíptica.

Falta por relacionar las intensidades

\[
\frac{I^{\prime}}{I}=\frac{\left|A_{\|}^{\prime}\right|^{2}+\left|A_{\perp}^{\prime}\right|^{2}}{|\mathbf{A}|^{2}}=0.92
\notag \]

El \(8 \%\) que se pierde es muy poco: los dieléctricos apenas reflejan en incidencias próximas a la normal.

P

Problema \(\PageIndex{15}\)

Un haz plano monocromático de longitud de onda \(\lambda\) incide desde un medio transparente de indice de refracción \(n\) al vacio, con ángulo de incidencia \(\theta=60^{\circ}\) (11.5). La onda está linealmente polarizada de modo perpendicular al plano de incidencia. Calcúlese el indice de refracción n para que la superposición del haz incidente con el reflejado produzca un campo eléctrico nulo \(\left(|\mathbf{E}|^{2}=0\right)\), en cualquier instante de tiempo en el plano \(z=-\frac{2 \lambda}{3} .(\lambda\) es la longitud de onda en el medio).

Respuesta

Tenemos que escribir una expresión para ambas ondas, sumarlas e imponer su anulación para todo instante en el plano \(z=-\frac{2 \lambda}{3}\). La onda incidente es

\[
\mathbf{A} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)} \mathbf{u}_{y}
\notag \]

donde \(\mathbf{k}=k \sin \theta \mathbf{u}_{x}+k \cos \theta \mathbf{u}_{z} \operatorname{con} k=|\mathbf{k}|=n \frac{\omega}{c}=\frac{2 \pi}{\lambda}\) ( \(\lambda\) es la longitud de onda en el medio). La onda reflejada tiene un vector de ondas con signo cambiado en la componente \(z: \mathbf{k}^{\prime \prime}=k \sin \theta \mathbf{u}_{x}-k \cos \theta \mathbf{u}_{z}\)

\[
r_{\perp} A e^{i\left(\mathbf{k}^{\prime \prime} \cdot \mathbf{r}-\omega t\right)} \mathbf{u}_{y}
\notag \notag \notag \]

Sumamos para obtener

\[
\mathbf{E}=A\left(e^{i k \cos \theta z}+r_{\perp} e^{-i k \cos \theta z}\right) e^{i(k \sin \theta x-\omega t)} \mathbf{u}_{y}
\notag \]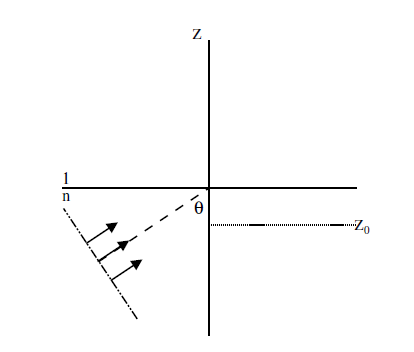

Figura \(\PageIndex{5}\): Interfaz medio transparente - vacío.

El primer paréntesis debe ser cero si queremos que el campo se anule para todo \(t\). Eso es porque la parte dependiente del tiempo es suma de dos funciones (seno y coseno) que no se anulan a la vez nunca. En definitiva

\[
r_{\perp}=-e^{i 2 k \cos \theta z}
\notag \]

utilizando que \(z_{0}=-\frac{2 \lambda}{3}\) y \(\theta=60^{\circ}\) obtenemos

\[
r_{\perp}=-e^{-i \frac{4 \pi}{3}}
\notag \]

para ligarlo con el índice de refracción del medio inicial necesitamos una expresión para \(r_{\perp}\). Advertimos que es un caso de reflexión total (el coeficiente es un número complejo de módulo unidad), y las expresiones son entonces

\[
\begin{aligned}
r_{\perp} &=e^{i \delta_{\perp}} \\
\tan \left(\frac{\delta_{\perp}}{2}\right) &=-\frac{\sqrt{\sin ^{2} \theta-\left(\frac{1}{n}\right)^{2}}}{\cos \theta}
\end{aligned}
\notag \]

y como \(\delta_{\perp}=-\frac{4 \pi}{3}+\pi\) se despeja \(n=\sqrt{3 / 2} .\)

Exercise \(\PageIndex{1}\)

(fórmulas de Fresnel) Se tienen dos medios isótropos y homogéneos. El primero es un dieléctrico transparente de índice \(n_{1}\). Sobre la superficie que los separa incide con ángulo \(\theta_{i}\) una onda plana monocromática linealmente polarizada a \(45^{\circ}\) con el plano de incidencia. Si \(\theta_{i}=0\) ipuede la luz reflejada estar circularmente polarizada? Sabiendo que para \(\theta_{i} \neq 0\) la luz reflejada está elípticamente polarizada y la reflectividad es menor que la unidad, indique la naturaleza del segundo medio.

Answer

Para responder a la pregunta por la polarización de la luz reflejada aplicamos las fórmulas de FRESNEL: \(\theta_{i}=0\) implica \(r_{\|}=-r_{\perp}\). Nunca podremos tener un haz reflejado polarizado circularmente, ya que al cumplirse \(\left(\begin{array}{l}R_{\|} \\ R_{\perp}\end{array}\right)=r_{\perp}\left(\begin{array}{c}-A_{\perp} \\ A_{\perp}\end{array}\right)\) la amplitud reflejada es proporcional a un vector real, y por lo tanto el haz es linealmente polarizado. Para caracterizar la naturaleza óptica de un medio tenemos que especificar la parte real e imaginaria del índice de refracción. Por ser la luz reflejada elíptica, puede ocurrir que:

- segundo medio transparente, pero en reflexión total \(\left(n_{1}>n_{2}\right.\) y \(\left.\theta_{i}>\theta_{c}\right)\) o bien

- segundo medio absorbente \(\left(\kappa_{2} \neq 0\right)\).

El hecho de que en el primer caso \(\mathcal{R}=1\) indica que la respuesta es la segunda opción.

P

Problema \(\PageIndex{17}\)

Problema El tensor dieléctrico para cierto material es

\[
\hat{\epsilon}=\epsilon_{0}\left(\begin{array}{ccc}
a & i b & 0 \\
-i b & a & 0 \\
0 & 0 & d
\end{array}\right)
\notag \notag \notag \]

siendo \(a, b, d\) números reales con \(a>b>0 y d \neq 0\). Calcular los posibles vectores de onda y las polarizaciones correspondientes para una onda armónica plana con vector de ondas en el ejez.

Respuesta

El medio cumple \(\hat{\epsilon}^{+}=\hat{\epsilon}\) (matriz hermítica). Es transparente y ópticamente activo. Vamos a atacar el problema como el de los medios no activos, utilizando las ecMm. En particular se llegaba a la relación

\[
\left(\mathbf{k} \cdot \mathbf{E}_{0}\right) \mathbf{k}-\mathbf{k}^{2} \mathbf{E}_{0}^{2}+\mu_{0} \omega \hat{\epsilon} \mathbf{E}_{0}=0
\notag \notag \notag \]

como \(k_{x}=k_{y}=0\) y \(k_{z}=k\) y utilizando \(\mu_{0} \epsilon_{0}=c^{-2}\) la matriz queda

\[
\left(\begin{array}{ccc}
\left(\frac{\omega}{c}\right)^{2} a-k^{2} & i\left(\frac{\omega}{c}\right)^{2} b & 0 \\
-i\left(\frac{\omega}{c}\right)^{2} b & \left(\frac{\omega}{c}\right)^{2} a-k^{2} & 0 \\
0 & 0 & \left(\frac{\omega}{c}\right)^{2} d
\end{array}\right)\left(\begin{array}{c}
E_{0 x} \\
E_{0 y} \\
E_{0 z}
\end{array}\right)=0
\notag \notag \notag \]

para que \(|\mathrm{M}|=0\) los valores que puede tomar \(k\) son dos:

\[
k_{\pm}=\frac{\omega}{c} \sqrt{a \pm b}
\notag \notag \notag \]

entonces

\[
\mathrm{M}\left(k_{+}\right)=\left(\frac{\omega}{c}\right)^{2}\left(\begin{array}{ccc}
-b & i b & 0 \\
-i b & -b & 0 \\
0 & 0 & d
\end{array}\right)
\notag \notag \notag \]

el vector \(\mathbf{E}_{0}\) que satisface la ecuación de autovalores \(\mathrm{M}\left(k_{+}\right) \mathbf{E}_{0}=0 \mathrm{es}\)

\[
\mathbf{E}_{0}=\mathbf{A}_{+}\left(\begin{array}{c}
1 \\
-i \\
0
\end{array}\right)
\notag \notag \notag \]

\section{Ejercicios y problemas}

con \(\mathbf{A} \in \mathcal{C}\). Es luz circular dextrógira. Siguiendo los mismos pasos se halla

\[
\mathbf{E}_{0}=\mathbf{A}_{-}\left(\begin{array}{c}
1 \\
+i \\
0
\end{array}\right)
\notag \notag \notag \]

para la ecuación de autovalores \(\mathrm{M}\left(k_{-}\right) \mathbf{E}_{0}=0\) (luz circularmente polarizada levógira).

Cuando estudiábamos los medios no activos teníamos luz linealmente polarizada. En medios activos la polarización será en general elíptica.

P

Problema \(\PageIndex{18}\)

actividad óptica Si en el problema anterior \(\mathbf{E}(z=0, t)\) está linealmente polarizado según el eje \(x\) calcular el estado de polarización en \(z=d\).

Respuesta

\[
\mathbf{E}(0, t) \propto \mathbf{u}_{x}
\notag \notag \notag \]

dicho de otro modo

\[
\mathbf{E}(0, t)=\left(\begin{array}{c}
E_{0} \\
0 \\
0
\end{array}\right) e^{-i \omega t}
\notag \notag \notag \]

hemos encontrado que las ondas que se propagan según el eje \(z\) deben ser combinaciones lineales de las ondas que escribimos en el problema anterior. Es decir

\[
\mathbf{E}(z, t)=\mathbf{A}_{+}\left(\begin{array}{c}
1 \\
-i \\
0
\end{array}\right) e^{i\left(k_{+} z-\omega t\right)}+\mathbf{A}_{-}\left(\begin{array}{c}
1 \\
i \\
0
\end{array}\right) e^{i\left(k_{-} z-\omega t\right)}
\notag \notag \notag \]

vamos a determinar los coeficientes de la combinación lineal con ayuda de las condiciones del problema

\[
\mathbf{E}(0, t)=\left(\begin{array}{c}
\mathbf{A}_{+}+\mathbf{A}_{-} \\
i\left(\mathbf{A}_{-}-\mathbf{A}_{+}\right) \\
0
\end{array}\right) e^{-i \omega t}
\notag \notag \notag \]

en consecuencia \(\mathbf{A}_{+}=\mathbf{A}_{-}=\frac{E_{0}}{2} .\) El campo es

\[
\mathbf{E}(d, t)=\frac{E_{0}}{2}\left(\left(\begin{array}{c}
1 \\
-i \\
0
\end{array}\right) e^{i\left(k_{+} d\right)}+\left(\begin{array}{c}
1 \\
i \\
0
\end{array}\right) e^{i(k d)}\right) e^{-i \omega t}
\notag \notag \notag \]

una posible forma de saber el estado de polarización es sacar la fase así

\[
\mathbf{E}(d, t)=E_{0}\left(\begin{array}{c}
\cos \theta \\
\sin \theta \\
0
\end{array}\right) e^{i \frac{\left(k_{+}+k_{-}\right)}{2} d} e^{-i \omega t}
\notag \notag \notag \]

\(\operatorname{con} \theta=\left(k_{+}-k_{-}\right) \frac{d}{2}\). En esta expresión resulta muy claro que la luz es linealmente polarizada, formando un ángulo \(\theta\) con el eje \(x\).

La dirección de polarización va rotando a medida que el haz se va propagando. Esto es lo que recibe el nombre de actividad óptica.

P

Problema \(\PageIndex{19}\)

Una onda armónica plana incide desde el vacío sobre un medio anisótropo uniáxico siendo el ángulo de incidencia distinto de cero. El eje óptico es perpendicular al plano de separación entre el vacio y el medio, y \(n_{e}>n_{o}\). Se desea saber el estado de polarización de la onda refractada cuyo vector de ondas forme el mayor ángulo con la normal a la superficie.

Respuesta

En general se propagarán dos ondas con polarizaciones distintas. Para determinar los vectores de onda tenemos que cortar la superficie de vectores de onda con el plano de incidencia. Se trata de una superficie bifoliada, una de cuyas secciones es una semicircunferencia y una semielipse. Como el radio del elipsoide de vectores de onda en el plano perpendicular al eje óptico (que es su eje de revolución) es \(n_{e} \frac{\omega}{c}\) sabemos que la elipse será más grande que la circunferencia. La proyección sobre el eje \(x\) de ambas ondas es la misma. La ordinaria se traza unívocamente dibujando el extremo del vector en la circunferencia y la extraordinaria poniéndolo en la elipse.

De las dos, la que mayor ángulo forma con la normal es la ordinaria. Su polarización es lineal perpendicular al plano formado por \(\mathbf{k}_{o} \mathrm{y}\) el eje óptico, es decir, en nuestra elección de ejes, sobre el eje \(y\).

Problema \(\PageIndex{20}\)

Si se observa un objeto muy lejano a través de una lámina planoparalela de un medio anisótropo se ve una imagen en lugar de las dos imágenes que se verían si el objeto estuviera muy cercano. ¿Por qué? Considérese que sobre la lámina incide un haz de rayos paralelos procedentes de un objeto puntual en el infinito y que se observa en el plano focal imagen de una lente delgada convergente.

Respuesta

La luz llega en forma de oap, según la hipótesis sugerida en el enunciado. Esa onda, en general, dará lugar a dos ondas distintas dentro del medio anisótropo, que a su vez se propagarán separadamente a la salida. Si nos dicen que sólo se ve una a la salida, quiere decir que las dos tienen la misma dirección (es decir, que sólo hay un vector de ondas a la salida: \(\mathbf{k}^{\prime \prime}\) ).

Sabemos que \(\mathbf{k}_{t}\) se conserva (condiciones de contorno). En la primera cara de la lámina

\[
\mathbf{k}_{t}=\mathbf{k}_{t}^{\prime}
\notag \notag \notag \]

Por ser la lámina planoparalela podemos escribir la igualdad

\[
\mathbf{k}_{t}=\mathbf{k}_{t}^{\prime}=\mathbf{k}_{t}^{\prime \prime}
\notag \notag \notag \]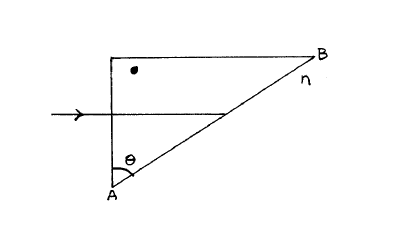

Figura \(\PageIndex{6}\): Prisma anisótropo uniáxico.

tanto \(\mathbf{k}\) como \(\mathbf{k}^{\prime \prime}\) están en un medio isótropo. Las tres componentes de \(\mathbf{k}^{\prime \prime}\) están especificadas, al tener una condición sobre \(\mathbf{k}_{t}^{\prime \prime} \mathrm{y}\) la condición (que no se verifica para \(\mathbf{k}^{\prime}\) )

\[
\left|\mathbf{k}^{\prime \prime}\right|=n \frac{\omega}{c}
\notag \notag \notag \]

El reparto energético entre los rayos emergentes depende del eje óptico, el estado de polarización de la onda incidente y los ángulos de incidencia, por lo que no podemos precisar nada sobre él.

P

Problema \(\PageIndex{21}\)

Una onda armónica plana incide normalmente sobre una de las caras de un prisma tal como indica la figura. El prisma está hecho de un medio anisótropo uniáxico con el eje óptico perpendicular al plano de la figura. Calcular el índice de refracción \(n\) del medio que rodea al prisma para que la onda ordinaria sufra reflexión total en la cara \(A B\) mientras que la extraordinaria no la sufre. Considérense \(\theta=60^{\circ}, n_{o}=1.66\) y \(n_{e}=1.49\).

Respuesta

Pasos a seguir: introducir la luz dentro del prisma. Las componentes tangenciales dentro del prisma, por aplicación de las condiciones de contorno, serán (las de ambas ondas) cero, de modo que la propagación continuará en la dirección de incidencia.

\[
\begin{aligned}
&\left|\mathbf{k}_{o}\right|=n_{o r} \frac{\omega}{c} \\
&\left|\mathbf{k}_{e}\right|=n_{e x} \frac{\omega}{c}
\end{aligned}
\notag \]

Tenemos que imponer que la onda ordinaria sufra reflexión total: la componente tangencial del vector de ondas debe ser tal que no haya ninguna componente tangencial en el segundo medio que la pueda igualar

\[
\begin{aligned}
\left|\mathbf{k}_{o}\right| \sin \theta &=n_{o} \frac{\omega}{c} \sin \theta \geq \frac{\omega}{c} n \\
n_{o} \sin \theta & \geq n
\end{aligned}
\notag \]

La condición análoga para la onda extraordinaria es

\[
n>n_{e} \sin \theta
\notag ]

combinando ambas desigualdades

\[
\begin{aligned}
n_{o} \sin \theta & \geq n>n_{e} \sin \theta \\
1.44 & \geq n>1.29
\end{aligned}
\notag \]

Figure \(\PageIndex{7}\): Los polarizadores del problema, \(P_{1}, P_{2}\) y \(P_{3}\) respectivamente.

ése es el intervalo de índices posibles.

Comentario: este prisma es un polarizador (a la salida tenemos luz linealmente polarizada independientemente del estado de polarización de la onda de incidencia). La componente ordinaria no progresa más allá del prisma en la dirección de interés (se suele colocar otro prisma debajo para enderezar el rayo que nos interesa).

P

Problema \(\PageIndex{22}\)

Supóngase que un polarizador lineal gira a una velocidad angular \(\Omega\) entre un par de polarizadores cruzados entre sí (figura 11.7). Demuéstrese que la intensidad luminosa emergente es

\[
I(t)=\frac{I_{0}}{8}(1-\cos 4 \Omega t)
\notag \]

donde \(I_{0}\) es la intensidad emergente del primer polarizador.

Respuesta

La forma más cómoda es escribir las matrices y aplicarlas al estado de polarización inicial. Vamos a suponer que la polarización inicial es lineal y está vibrando según el eje \(x\). Si \(I_{0}=|\mathbf{A}|^{2}\)

\[
\mathbf{A}=\sqrt{I_{0}}\left(\begin{array}{l}
1 \\
0
\end{array}\right)
\notag \]

ésta es la amplitud que abandona el primer polarizador. Las matrices son

\[
\mathrm{P}_{3}=\left(\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right)
\notag \]

\[
P_{2}=\left(\begin{array}{cc}
\cos ^{2} \Omega t & \sin \Omega t \cos \Omega t \\
\sin \Omega t \cos \Omega t & \sin ^{2} \Omega t
\end{array}\right)
\notag \]

La amplitud emergente debe ser

\[
\begin{aligned}
\mathbf{A}^{\prime} &=\mathrm{P}_{3} \mathrm{P}_{2} \mathbf{A} \\
&=\sqrt{I_{0}}\left(\begin{array}{c}
0 \\
\sin \Omega t \cos \Omega t
\end{array}\right)
\end{aligned}
\notag \]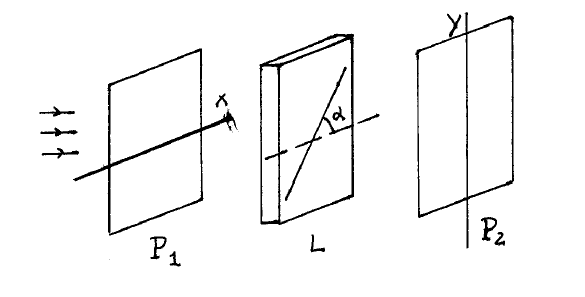

Figura \(\PageIndex{8}\): Sistema de polarizadores.

y la intensidad correspondiente

\[
\begin{aligned}
I^{\prime} &=I_{0}(\sin \Omega t \cos \Omega t)^{2} \\
&=\frac{I_{0}}{4} \sin ^{2} 2 \Omega t \\
&=\frac{I_{0}}{8}(1-\cos 4 \Omega t)
\end{aligned}
\notag \]

Sin hacer matrices, se puede razonar que el haz de luz a la salida del \(P_{2}\) estará vibrando en la dirección de su eje, es decir

\[
\mathbf{A}^{\prime \prime}=\sqrt{I_{0}} \cos \Omega t\left(\begin{array}{c}
\cos \Omega t \\
\sin \Omega t
\end{array}\right)
\notag \]

el \(P_{3}\) sólo deja pasar la componente \(y\), por lo que

\[
\mathbf{A}^{\prime}=\sqrt{I_{0}} \cos \Omega t\left(\begin{array}{c}
0 \\
\sin \Omega t
\end{array}\right)
\notag \]

que es el resultado al que hemos llegado usando el formalismo matricial.

P

Problema \(\PageIndex{23}\)

Sea el sistema de la figura. \(P_{1}\) y \(P_{2}\) son dos polarizadores cuyos ejes de transmisión coinciden con el \(x\) y el y, respectivamente, y L es una lámina planoparalela de un medio anisótropo uniáxico con eje óptico paralelo a las caras, formando un ángulo \(\alpha\) con el x. Suponiendo que perpendicularmente a \(P_{1}\) inciden sobre el sistema dos ondas planas monocromáticas de longitudes de onda \(\lambda_{1} y \lambda_{2}\), icuánto deberán valer \(\alpha\) y el espesor de la lámina para que el sistema deje pasar únicamente \(\lambda_{1}\) con transmisión máxima eliminando completamente el otro haz?

Respuesta

Siempre podemos calcular las matrices de \(L\) y \(P_{2}\) y aplicarlas al estado de polarización procedente del primer polarizador, \(P_{1}\).El ángulo del eje óptico de la lámina con el eje \(x\) lo etiquetamos \(\alpha\), por lo que el ángulo con el eje \(y\) es \(\bar{\alpha}=\alpha-\pi / 2\).

\[
\mathbf{A}=\sqrt{I}\left(\begin{array}{l}
1 \\
0
\end{array}\right)
\notag \]

Figure \(\PageIndex{9}\): Secciones por el plano \(x y\) de \(P_{1}, L\) y \(P_{2}\) respectivamente

La matriz de la lámina retardadora depende de la longitud de onda,

\[
\mathrm{L}=\left(\begin{array}{cc}
\cos ^{2} \bar{\alpha}+e^{i \delta} \sin ^{2} \bar{\alpha} & \cos \bar{\alpha} \sin \bar{\alpha}\left(1-e^{-i \delta}\right) \\
\cos \bar{\alpha} \sin \bar{\alpha}\left(1-e^{-i \delta}\right) & \sin ^{2} \bar{\alpha}+e^{i \delta} \cos ^{2} \bar{\alpha}
\end{array}\right)
\notag \]

\(\operatorname{con} \delta=\frac{2 \pi}{\lambda}\left(n_{0}-n_{e}\right) d\)

\[
P_{2}=\left(\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right)
\notag \]

Entonces

\[
\mathbf{A}^{\prime}=P_{2} L \mathbf{A}
\notag \]

de donde

\[
\begin{aligned}
\mathbf{A}^{\prime} &=\sqrt{I} \sin \bar{\alpha} \cos \bar{\alpha}\left(1-e^{-i \delta}\right)\left(\begin{array}{l}
0 \\
1
\end{array}\right) \\
I^{\prime} &=I \sin ^{2} 2 \bar{\alpha} \sin ^{2} \frac{\delta}{2}
\end{aligned}
\notag \]

pero tenemos \(\delta_{i}=\frac{2 \pi}{\lambda_{i}}\left(n_{o}-n_{e}\right) d\).

1. Si \(I_{\lambda_{2}}^{\prime}=0\) entonces \(\sin \frac{\delta_{2}}{2}=0\). Por tanto \(\delta_{2}=2 \pi m\) con \(m \in \mathcal{Z}\). Ya tenemos una condición sobre \(d\) de la lámina.

\[
d=\frac{m \lambda_{2}}{n_{o}-n_{e}}
\notag \]

Fijémonos en que para que la luz llegue según el eje \(x\) al segundo polarizador, es necesario que la lámina no cambie el estado de polarización de la luz incidente, es decir, que \(\delta=2 \pi m\).

2. Para la segunda condición es necesario que se maximicen los dos factores

\[
\sin 2 \bar{\alpha}=\pm 1
\notag \]

de donde \(\alpha=\pm \frac{\pi}{4} \mathrm{y}\)

\[
\sin ^{2}\left(\frac{\delta_{1}}{2}\right)
\notag \]

\section{Ejercicios y problemas}

debe ser máximo también, de donde

\[
\begin{aligned}
\delta_{1} &=(2 M+1) \pi \\
&=2 \pi M \frac{\lambda_{2}}{\lambda_{1}} \frac{\left(n_{o}-n_{e}\right)_{\lambda_{2}}}{\left(n_{o}-n_{e}\right)_{\lambda_{1}}}
\end{aligned}
\notag \]

con \(M \in \mathcal{Z}\). Si suponemos que la diferencia de índices es la misma para ambas longitudes de onda

\[
\delta_{1}=2 \pi M \frac{\lambda_{2}}{\lambda_{1}}
\notag \]

todo lo que podeos escribir es

\[
\frac{2 M+1}{2 m}=\frac{\lambda_{2}}{\lambda_{1}}
\notag \]

que no podríamos verificarlo siempre, porque a un lado tenemos un racional y a otro un real. Pero tenemos dos escapatorias

a) Los racionales son densos en los reales, y podemos aproximar un real cada vez más eligiendo m y \(M\) cada vez más grandes.

b) En el mundo real, donde no se puede medir con precisión infinita, el cociente de la izquierda es en definitiva también un racional.

Si tomamos un ejemplo práctico,

\[
\begin{aligned}
&\lambda_{1}=589.6 \mathrm{~nm} \\
&\lambda_{2}=589.0 \mathrm{~nm}
\end{aligned}
\notag \]

y por simplificar, \(M=m\), al despejar \(m\) de

\[
\frac{2 m+1}{m}=\frac{\lambda_{2}}{\lambda_{1}}
\notag \]

obtenemos \(m \simeq 491\) y \(I_{1}^{\prime}=0.99995 I \simeq I\)

P

Problema \(\PageIndex{24}\)

Problema Un haz de luz esta formado por una mezcla de luz linealmente polarizada (intensidad \(I_{p}\) ) y luz no polarizada (intensidad \(I_{n p}\) ). Indíquese cómo pueden obtenerse \(I_{p}\) e \(I_{n p}\) a partir de la medida de la intensidad que atraviesa un polarizador que puede orientarse como convenga.

Respuesta

Tenemos una combinación de luz linealmente polarizada y luz natural.

\[
I^{\prime}=\frac{I_{n p}}{2}+I_{p} \cos ^{2} \theta
\notag \]

Variando el \(\theta\) podemos obtener las dos cantidades. Si representamos la intensidad emergente frente a la posición del polarizador, \(I^{\prime}(\theta)\) obtenemos una curva \(\cos ^{2} \theta\)

Tenemos una serie de máximos \(I_{\max }^{\prime}\) y de mínimos \(I_{\min }^{\prime}\)

\[
\begin{aligned}
I_{\max }^{\prime} &=\frac{I_{n p}}{2}+I_{p} \\
I_{\min }^{\prime} &=I_{n p}
\end{aligned}
\notag \]

con lo que

\[
\begin{aligned}
I_{n p} &=2 I_{\min }^{\prime} \\
I_{p} &=I_{\max }^{\prime}-I_{\min }^{\prime}
\end{aligned}
\notag \]

P

Problema \(\PageIndex{25}\)

Un haz plano de intensidad \(I_{0}\) incide con ángulo \(\alpha\) sobre un plano en el que se encuentran dos rendijas separadas una distanciad.

1. Calcúlese la intensidad en un plano paralelo al que contiene la rendijas y suficientemente alejado.

2. En una de las rendijas se coloca una lámina absorbente cuya transmitancia es \(0.01\). Determínese la visibilidad.

Respuesta

1. Se cumple la hipótesis \(x, d \ll D\). Vamos a suponer \(n=1\). Hay ya una diferencia de fase ya al llegar al propio plano que contiene las aberturas.Tenemos que calcular ese desfase previo para considerarlo en el argumento del coseno del término de interferencia, \(g_{2}-g_{1}=k\left(r_{2}-r_{1}\right)\). La diferencia de fases al llegar a las aberturas es \(\Delta\). El camino óptico para la onda superior es pues \(r_{1}+\Delta\) y para la inferior, \(r_{2}\). La diferencia de fases al llegar a la pantalla es, pues

\[
d i f=k\left(r_{2}-r_{1}\right)-k \Delta
\notag \notag \notag \]

\(\Delta\) se obtiene fácilmente con argumentos geométricos: \(\Delta=d \sin \alpha\). Si aprovechamos la condición \(x, d \ll D\) podemos además aproximar \(r_{2}\) y \(r_{1}\) y la diferencia de fase queda

\[
d i f \simeq \frac{2 \pi}{\lambda} \frac{x d}{D}-k d \sin \alpha
\notag \notag \notag \]

en virtud de \(x, d \ll D\) podemos escribir, también, \(I_{1} \simeq I_{2}\). La expresión final es

\[
I=2 I_{2}\left(1+\cos \left(\frac{2 \pi}{\lambda} \frac{x d}{D}-k d \sin \alpha\right)\right)
\notag \notag \notag \]

2. Ponemos una lámina absorbente, por ejemplo en la abertura superior. La intensidad que la atraviesa es un \(1 \%\) de la que incide sobre ella. \(I_{1}^{\prime}=0.01 I_{1} \simeq 0.01 I_{2}\). El enunciado no nos da ninguna indicación sobre el efecto de esta lámina absorbente sobre la fase, por lo que ponemos una cantidad indeterminada, \(\delta\)

\[
I=I_{2}\left(1+0.01+2 \sqrt{0.01} \cos \left(\frac{2 \pi}{\lambda} \frac{x d}{D}-k d \sin \alpha+\delta\right)\right)
\notag \notag \notag \]

la visibilidad es

\[
\begin{aligned}
V &=\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }} \\
I_{\max } &=1.21 I_{2} \\
I_{\min } &=0.81 I_{2} \\
V &=0.198
\end{aligned}
\notag \notag \notag \]

la lámina absorbente hace que los mínimos ya no sean nulos, y por lo tanto, la visibilidad no es buena.

P

Problema \(\PageIndex{26}\)

(Young con una fuente extensa) En el interferómetro de YOUNG de la figura 11.10, las dos rendijas son iluminadas por una fuente extensa. La intensidad que se obtiene en la pantalla debida a una fuente puntual en \(x^{\prime}\) es, si \(x^{\prime} \ll B\),

\[
d I_{x^{\prime}}=2 J_{0}\left\{1+\cos \left[\frac{2 \pi}{\lambda} d\left(\frac{x}{D}+\frac{x^{\prime}}{B}\right)\right]\right\} d x^{\prime}
\notag \]

Donde \(J_{0}\) es una constante.

1. Calcular la figura interferencial considerando la fuente extensa entre \(-a / 2\) y \(a / 2\) como un continuo de fuentes puntuales incoherentes entre sí.

2. Calcular la visibilidad.

Respuesta

Según dice el enunciado

\[
d I_{x^{\prime}}=2 J_{0}\left(1+\cos \left(\frac{2 \pi}{\lambda} d\left(\frac{x}{D}+\frac{x^{\prime}}{B}\right)\right)\right) d x^{\prime}
\notag \]

el término \(\frac{x^{\prime}}{B}\) en el argumento del coseno es la diferencia de fase debida a que la fuente puntual no está en el origen (esta fórmula sirve para la intensidad creada por uno cualquiera de los puntos incoherentes de la fuente extensa) y las ondas no llegan a la abertura con igual fase. Si se cumple que \(x^{\prime}, d^{\prime} \ll B\)

\[
k\left(r_{2}^{\prime}-r_{1}^{\prime}\right) \simeq \frac{2 \pi d x^{\prime}}{B}
\notag \]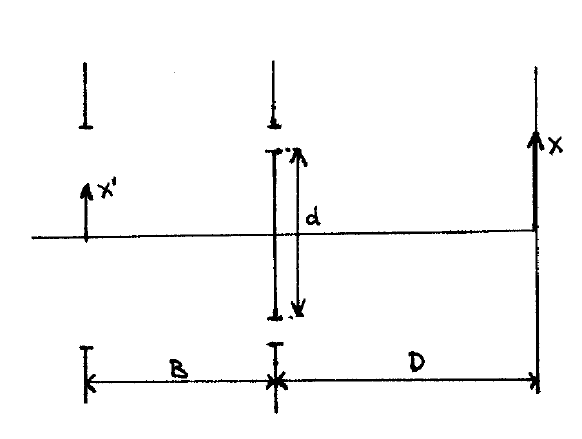

Figura \(\PageIndex{10}\): Interferómetro de Young.

En virtud de la incoherencia de las fuentes puntuales sobre la pantalla de observación no se suman amplitudes (puesto que no hay interferencia entre las ondas provenientes de distintos puntos de la fuente extensa) sino intensidades.

\[
I=\int_{-\frac{a}{2}}^{\frac{a}{2}} d I_{x^{\prime}}
\notag \]

Haciendo la integral y teniendo en cuenta que \(\sin A-\sin B=2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\) el resultado es

\[
I=2 J_{0} a\left(1+\operatorname{sinc}\left(\frac{\pi}{\lambda} \frac{a d}{B}\right) \cos \left(\frac{2 \pi}{\lambda} \frac{x d}{D}\right)\right)
\notag \]

donde hemos introducido la función seno cardinal, sinc \((x)=\frac{\sin x}{x}\). Para hallar la visibilidad calculamos los máximos y mínimos, teniendo en cuenta que el seno cardinal cambia de signo...

\[
\begin{aligned}
&I_{\max }=2 J_{0} a\left(1+\left|\operatorname{sinc}\left(\frac{\pi}{\lambda} \frac{a d}{B}\right)\right|\right) \\
&I_{\min }=2 J_{0} a\left(1-\left|\operatorname{sinc}\left(\frac{\pi}{\lambda} \frac{a d}{B}\right)\right|\right)
\end{aligned}
\notag \]

De donde \(V=\left|\operatorname{sinc}\left(\frac{\pi}{\lambda} \frac{a d}{B}\right)\right|\) (figura 11.11). La función crece a medida que el argumento decrece. Cuanto mayor es el tamaño de la fuente peor es la visibilidad. La visibilidad también desciende si se separan las aberturas ( \(d\) crece) o si se reduce la distancia de la fuente a éstas \((B)\). El primer mínimo nulo,

\[
\frac{\pi a d}{\lambda B}=\pi
\notag \]

marca un criterio cuantitativo razonable para distinguir una zona de buena visibilidad de otra de visibilidad mucho más pobre.

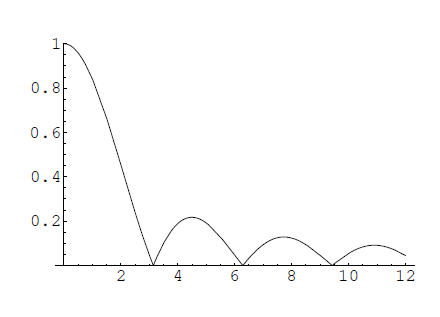
Figura \(\PageIndex{11}\): \(V=V\left(\frac{\pi}{\lambda} \frac{a d}{B}\right)\)

Ejemplo

Si se tienen los datos \(a=1 m m, B=10 \mathrm{~cm}, \lambda=600 n m\) ¿cuál es la separación entre orificios \((d)\) que hace \(V=0 ?\).

\[
\begin{aligned}
\frac{\pi a d}{\lambda B} &=\pi \\
d &=\frac{\lambda B}{a} \\
&=0.06 \mathrm{~mm}
\end{aligned}
\notag \]

Para \(V \neq 0\) necesitamos \(d<0.06 \mathrm{~mm}\). El interferómetro de YOUNG es muy restrictivo cuando opera con fuentes extensas. Eso hace que se puedan medir distancias (cualquiera de las que están en el argumento del coseno) con gran precisión.

El tipo de condiciones que hemos visto aparece en la bibliografía bajo el epígrafe "coherencia espacial".

Por otra parte, hay que subrayar que si bien nuestro interés aquí ha sido encontrar zonas de \(V\) alto (para poder observar mejor la interferencia) hay muchas aplicaciones de medida que se basan en el efecto que acabamos de ver de rápida pérdida de visibilidad. Si conocemos los datos del interferómetro \((d, \lambda, B)\) podemos medir el tamaño de la fuente separando las aberturas hasta que \(V=0\) : entonces \(a=\frac{\lambda B}{d}\). Esta técnica se aplica a la determinación del diámetro aparente de las estrellas (conocida su distancia...) y entonces el dispositivo se llama interferómetro estelar de MICHELSON.

Problema \(\PageIndex{27}\)

(interferencia con un espejo) En el montaje de la figura 11.12 se tienen dos fuentes puntuales incoherentes a distancias \(d_{1} y d_{2}\) del espejo que emiten con longitudes de onda \(\lambda_{1} y \lambda_{2}\) respectivamente. Determinar la relación que debe haber entre \(d_{1}, d_{2}, \lambda_{1}\) y \(\lambda_{2}\) para que la figuras interferenciales de las dos fuentes coincidan.

Respuesta

Antes de atacar el problema en sí debemos calcular la figura interferencial creada por una sola fuente. La interferencia es posible porque la luz llega por dos vías a la pantalla:

1. directamente

2. reflejándose en el espejo \(11.1\) Resueltos

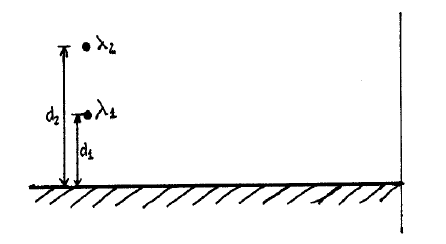
Figura \(\PageIndex{12}\): Interferencia con un espejo.

Siempre que se mantenga el requisito de diferencia de fase razonable, se podrá decir que estas dos ondas son coherentes.

Podemos hacer la misma operación que hicimos para simplificar el tratamiento del interferómetro de Michelson: sustituir los espejos por las imágenes que crean (pero teniendo en cuenta el desfase que introducen). En este caso, tendremos dos fuentes puntuales simétricas respecto al plano del espejo, y el sistema será equivalente a un interferómetro de YoUNG. Se cumple, como para este, que \(x, d \ll D\). Entonces

\[
I=2 I_{0}\left(1+\cos \left(\frac{2 \pi}{\lambda} \frac{2 x d}{D}+\delta\right)\right)
\notag \notag \notag \]

Donde \(\delta\) es el desfase (desconocido) introducido por la reflexión en un medio absorbente cual es el espejo. Por sencillez hemos considerado \(\mid\) coef reflexión \(\mid \simeq 1\); Si no fuese así habría que arrastrar por todas partes \(I_{2}=|r|^{2} I_{1}\).

Ahora podemos considerar las dos fuentes. Se cumple, respectivamente para cada una de ellas:

\[
\begin{aligned}
I &=2 I_{0}\left(1+\cos \left(\frac{2 \pi}{\lambda_{1}} \frac{2 x d_{1}}{D}+\delta_{1}\right)\right) \\
I &=2 I_{0}\left(1+\cos \left(\frac{2 \pi}{\lambda_{2}} \frac{2 x d_{2}}{D}+\delta_{2}\right)\right)
\end{aligned}
\notag \notag \notag \]

Como las fuentes son incoherentes entre sí, cada par de imágenes debido a una fuente crea su figura de interferencia independiente. Queremos que la distribución de intensidad en \(x\) sea igual para las dos fuentes:

\[
\frac{2 \pi}{\lambda_{1}} \frac{2 d x_{1}}{D}=\frac{2 \pi}{\lambda_{2}} \frac{2 x d_{2}}{D}
\notag \notag \notag \]

implica la condición

\[
\frac{d_{1}}{\lambda_{1}}=\frac{d_{2}}{\lambda_{2}}
\notag \notag \notag \]

además, debe cumplirse \(\delta_{1}=\delta_{2}(\bmod (2 \pi))\) para que los máximos coincidan.

P

Problema \(\PageIndex{28}\)

En un interferómetro de MICHELSON iluminado de forma normal a los espejos se tiene un máximo de intensidad para una frecuencia \(\omega\).

1. Calcular la frecuencia más próxima a \(\omega\) para la que también se tendría máxima intensidad para la misma separación entre los espejos.

2. Misma cuestión para un FABRY-PEROT.

Respuesta

Hay que imponer que para la misma configuración del interferómetro tengamos la misma figura para \(\omega^{\prime}\) y para \(\omega\), utilizando la condición de máximo, y seleccionar el \(\omega^{\prime}\) más próximo a \(\omega\). La condición de máximo para \(\theta=0\) es

\[
\frac{2 \pi}{\lambda} n 2 d+\delta=2 \pi M
\notag \]

en frecuencias \(\left(\frac{2 \pi}{\lambda}=\frac{\omega}{c}\right)\) tenemos

\[
\frac{\omega}{c} 2 n d+\delta=2 \pi M
\notag \]

de donde, para cada frecuencia, respectivamente

\[
\begin{aligned}
\omega &=\frac{c}{2 n d}(2 \pi M-\delta) \\
\omega^{\prime} &=\frac{c}{2 n d}\left(2 \pi M^{\prime}-\delta\right)
\end{aligned}
\notag \]

Las dos frecuencias más próximas a \(\omega\) para las que también se tiene máximo son las que cumplen \(M^{\prime}=M \pm 1\).

\[
\omega^{\prime}=\omega \pm \frac{\pi c}{n d}
\notag \]

Esta deducción la hemos hecho suponiendo que no había dispersión en el índice de refracción \(\left(n(\omega)=n\left(\omega^{\prime}\right)\right)\) ni en el desfase \(\left(\delta(\omega)=\delta\left(\omega^{\prime}\right)\right)\), lo que no es generalmente el caso.

El desarrollo del problema para un interferómetro de \(\mathrm{FP}\) es análogo.

Problema \(\PageIndex{29}\)

En un interferómetro de MICHELSON iluminado de forma normal a los espejos se tiene un máximo de intensidad para una frecuencia \(\omega\).

1. Calcular la frecuencia más próxima a \(\omega\) para la que también se tendría máxima intensidad para la misma separación entre los espejos.

2. Misma cuestión para un FABRY-PEROT.

Respuesta

Hay que imponer que para la misma configuración del interferómetro tengamos la misma figura para \(\omega^{\prime}\) y para \(\omega\), utilizando la condición de máximo, y seleccionar el \(\omega^{\prime}\) más próximo a \(\omega\). La condición de máximo para \(\theta=0\) es

\[
\frac{2 \pi}{\lambda} n 2 d+\delta=2 \pi M
\notag \]

en frecuencias \(\left(\frac{2 \pi}{\lambda}=\frac{\omega}{c}\right)\) tenemos

\[
\frac{\omega}{c} 2 n d+\delta=2 \pi M
\notag \]

de donde, para cada frecuencia, respectivamente

\[
\begin{aligned}
\omega &=\frac{c}{2 n d}(2 \pi M-\delta) \\
\omega^{\prime} &=\frac{c}{2 n d}\left(2 \pi M^{\prime}-\delta\right)
\end{aligned}
\notag \]

Las dos frecuencias más próximas a \(\omega\) para las que también se tiene máximo son las que cumplen \(M^{\prime}=M \pm 1\).

\[
\omega^{\prime}=\omega \pm \frac{\pi c}{n d}
\notag \]

Esta deducción la hemos hecho suponiendo que no había dispersión en el índice de refracción \(\left(n(\omega)=n\left(\omega^{\prime}\right)\right)\) ni en el desfase \(\left(\delta(\omega)=\delta\left(\omega^{\prime}\right)\right)\), lo que no es generalmente el caso.

El desarrollo del problema para un interferómetro de \(\mathrm{FP}\) es análogo.

 

Problema \(\PageIndex{30}\)

(poder resolutivo de un FP) La separación entre los dos espejos de un interferómetro de FABRY-PEROT es de \(1 \mathrm{~cm}\). Calcular la reflectancia de los espejos necesaria para distinguir las dos frecuencias \(\omega_{1}=3.543320 \times 10^{14} \mathrm{rad} / \mathrm{s} y \omega_{2}=3.543387 \times 10^{14} \mathrm{rad} / \mathrm{s}\). Supóngase que el medio en el interior del interferómetro es de indice \(n=1\), que la incidencia es normal y además despréciese el cambio de fase producido en las reflexiones.

Respuesta

El poder resolutivo del interferómetro tiene que ser tal que \(\omega_{1}\) y \(\omega_{2}\) estén resueltas:

\[
\frac{\lambda}{\Delta \lambda} \leq \frac{\pi}{2} M \sqrt{F}
\notag \]

Tenemos que encontrar el orden interferencial para poder despejar \(F\), pues \(F\) es la magnitud que podemos poner en función de \(\left|r_{1} r_{2}\right|\). Determinamos \(M\) imponiendo que a \(d=1 c m\) estemos observando máximos en estas longitudes de onda. La condición de máximo es

\[
\frac{2 \pi}{\lambda} n d \cos \theta+\delta=M \pi
\notag \]

Como el enunciado del problema no especifica \(n, \delta, \theta\), tomamos el caso sencillo \(n=1, \delta=\) \(0, \theta=0\). El orden interferencial es pues \(M=\frac{2 d}{\lambda}\). Pasamos de frecuencias a longitudes de onda \(\lambda_{i}=\frac{2 \pi c}{\omega_{i}}\). Para el cálculo del orden interferencial podemos usar en el denominador la media de las \(\lambda_{i}\) o un valor de una de ellas, puesto que son muy próximos. Con todo,

\[
M=3760
\notag \]

y \(F \geq 81\). Ahora entra en juego la expresión de \(F\)

\[
F=\frac{4\left|r_{1} r_{2}\right|}{\left(1-\left|r_{1} r_{2}\right|\right)^{2}}
\notag \]

Utilizando \(\left|r_{1} r_{2}\right|=x\) como incógnita y resolviendo la ecuación cuadrática, tenemos que para \(F=81\) (su valor mínimo) \(\left|r_{1} r_{2}\right|=0.80\) (hay otra solución, pero es superior a 1 , y por lo tanto, no aplicable a un coeficiente de reflexión). Por lo tanto, el resultado final es

\[
\left|r_{1} r_{2}\right| \geq 0.80
\notag \]

Problema \(\PageIndex{31}\)

(FP con medio anisótropo) Una onda armónica plana incide perpendicularmente sobre un interferómetro de FABRY-PEROT. El interior del interferómetro está ocupado totalmente por un medio anisótropo uniáxico cuyo eje óptico es paralelo a los espejos. La onda incidente puede estar linealmente polarizada vibrando según el eje óptico en un caso, y perpendicularmente al eje óptico en otro. En ambos casos la intensidad incidente es la misma. Razónese brevemente si la intensidad transmitida será o no la misma en los dos casos, para una separación arbitraria entre los espejos.

Respuesta

Para el interferómetro de FP se tiene

\[
I_{\max }=\frac{T_{\max }}{1+F \sin ^{2} \varphi} I
\notag \]

\(\operatorname{con} \theta=0\), el desfase entre ondas consecutivas es \(\varphi=\frac{2 \pi}{\lambda} n d+\delta\). Pero esto no vale en un medio anisótropo. Debemos expresarlo de otro modo

\[
\varphi=|\mathbf{k}| d+\delta
\notag \]

1. Luz vibrando según el eje óptico, onda extraordinaria: \(\left|\mathbf{k}_{e}\right|=n_{e} \frac{\omega}{c}\) en este caso particular en que \(\mathbf{k} \perp\) e.ó.

2. Luz perpendicular al eje óptico, onda ordinaria \(\left|\mathbf{k}_{o}\right|=n_{o} \frac{\omega}{c}\)

Figure \(\PageIndex{13}\): Difracción de Fresnel y de Fraunhoffer por una abertura circular.

 

El módulo de \(\mathbf{k}\) es distinto para cada onda \(\varphi\) es distinta dependiendo de la polarización y por lo tanto \(I^{\prime}\) es distinto para cada onda (polarización).

Seguro que \(T_{\max }\) y \(F\) también son distintos, pero este efecto será menor, ya que la figura de interferencia de un FP es sobre todo sensible a los cambios de fase.

Problema \(\PageIndex{32}\)

Un haz plano monocromático incide normalmente sobre una abertura circular de radio \(R\). Calcular el campo en el punto \(P\) a una distancia \(z\) del centro de la abertura usando las aproximaciones de FRESNEL y FRAUNHOFER.

Respuesta

La expresión para la onda difractada en la aproximación de FRESNEL es

\[
\hat{u}=\frac{e^{i k z}}{i \lambda z} \int d \xi d \eta t(\xi, \eta) u(\xi, \eta) e^{i \frac{k}{2 z}\left((x-\xi)^{2}+(y-\eta)^{2}\right)}
\notag \]

• el coeficiente de transmisión vale cero salvo sobre \((\xi, \eta) \in \Sigma\), que vale

• La iluminación es una oap.

\[
u=u_{0} e^{i \mathbf{k} \cdot \mathbf{r}}
\notag \]

• La incidencia es normal: La abertura est´a en z = 0, con lo que

\[
u=u_{0} e^{i k z}=u_{0}
\notag \]

El punto \(P\) tiene coordenadas \(0,0, z\), con lo que la integral resulta

\[
\hat{u}=\frac{e^{i k z}}{i \lambda z} u_{0} \int d \xi d \eta e^{i \frac{k}{2 z}\left(\xi^{2}+\eta^{2}\right)}
\notag \]

lo hacemos en polares, evidentemente \(\xi=\rho \cos \theta\) y \(\eta=\rho \sin \theta\). La integral en \(\rho\) se hace con el cambio de variable \(q=\rho^{2}\)

\begin{aligned}
\hat{u} &=\frac{e^{i k z}}{i \lambda z} u_{0} \pi \int_{0}^{R^{2}} d q e^{i \frac{k}{2 z} q} \\
&=\frac{e^{i k z}}{i \lambda z} u_{0} \pi \frac{1}{i \frac{k}{2 z}}\left(e^{i \frac{k}{2 z} R^{2}}-1\right) \\
&=u_{0} e^{i k z}\left(1-e^{i \frac{k R^{2}}{2 z}}\right)
\end{aligned}
\notag \]

Figure \(\PageIndex{14}\): La lente se desplaza paralelamente a la abertura

La fórmula válida para la aproximación de FRAUNHOFER se aplica siguiendo los mismo pasos

\begin{equation*}
\begin{aligned}
\hat{u} &=\frac{e^{i k\left(z+\frac{x^{2}+y^{2}}{2 z}\right)}}{i \lambda z} \int d \xi d \eta t(\xi, \eta) u(\xi, \eta) e^{-i \frac{k}{z}(x \xi+y \eta)} \\
&=\frac{e^{i k\left(z+\frac{x^{2}+y^{2}}{2 z}\right)}}{i \lambda z} \int_{\sum} d \xi d \eta u_{0} \\
&=\frac{e^{i k z}}{i \lambda z} u_{0} \pi R^{2}
\end{aligned}
\end{equation*}

Sabemos que la fórmula de FF es una aproximación de la de FRESNEL en el límite de \(z \rightarrow \infty\). Esta condición la podemos tener en cuenta desarrollando en sdp la expresión obtenida mediante la fórmula de FRESNEL:

\begin{equation*}
\begin{aligned}
\hat{u} & \simeq u_{0} e^{i k z}\left(1-1-i k \frac{k R^{2}}{2 z}+\ldots\right) \\
&=\frac{e^{i k z}}{i \lambda z} u_{0} \pi R^{2}
\end{aligned}
\end{equation*}

concluímos que el resultado vía \(\mathrm{FF}\) es consistente con la aproximación realizada.

Problema \(\PageIndex{33}\)

La figura de difracción de cierta abertura se observa en el plano focal imagen de una lente. Describir lo que le ocurre a la figura de difracción si la lente se desplaza paralelamente al plano que contiene la abertura.

Respuesta

Tenemos una abertura genérica iluminada con una onda genérica. Para responder a esta pregunta es necesario añadir la condición de que la lente sea infinita, algo que hemos tomado implícitamente como cierto en todo lo que hemos hecho hasta ahora, puesto que si no hubiéramos debido tener en cuenta la difracción causada por ella.

Lo que tiene de particular el plano focal imagen es que la luz que llega a cualquier punto ha tenido que arribar a la lente en forma de haz de rayos paralelos. Si bajamos la lente una distancia \(\Delta\), la imagen (cada punto) bajará una cantidad \(\Delta\). En principio la intensidad será la misma.

\section{Ejercicios y problemas}

La figura debe ser la misma pero desplazada en la misma medida en que desplacemos la lente.

Problema \(\PageIndex{34}\)

Sobre una abertura circular de radio \(R\) se coloca una transparencia descrita por el coeficiente de transmision \(t(x)=\alpha(1+q \cos (p x))\) siendo \(\alpha, p, q\) constantes. Calcular la figura de difracción de FRAUNHOFER en el plano focal imagen de una lente si la abertura se ilumina de forma normal con una onda plana y monocromática. Considérese \(p \gg 1 / R\).

Respuesta

El coeficiente de transmisión es ahora

\[
t(\xi, \eta)=\alpha(1+q \cos p \xi)
\notag \]

con \(p \gg \frac{1}{R}\). La fórmula a utilizar es la de \(\mathrm{FF}\)

\[
\hat{u}\left(x^{\prime}, y^{\prime}\right) \propto \int d \xi d \eta t(\xi, \eta) u(\xi, \eta) e^{-i \frac{k}{f^{\prime}}\left(x^{\prime} \xi+y^{\prime} \eta\right)}
\notag \]

podemos considerar \(u=u_{0} e^{i \mathbf{k} \cdot \mathbf{r}}=u_{0} e^{i k z}=u_{0}\) tomando el plano de la abertura como \(z=0\).

\[
\hat{u}\left(x^{\prime}, y^{\prime}\right) \propto \alpha u_{0} \int_{\Sigma} d \xi d \eta(1+q \cos (p \xi)) e^{-i \frac{k}{f^{\prime}}\left(x^{\prime} \xi+y^{\prime} \eta\right)}
\notag \]

Lo más cómodo es expresar el coseno en términos de exponenciales complejas

\[
\hat{u}\left(x^{\prime}, y^{\prime}\right) \propto \alpha u_{0} \int_{\Sigma} d \xi d \eta\left(1+\frac{q}{2}\left(e^{i p \xi}+e^{-i p \xi}\right)\right) e^{-i \frac{k}{f^{\prime}}\left(x^{\prime} \xi+y^{\prime} \eta\right)}
\notag \]

rompemos la integral según los términos del integrando

\[
\begin{array}{r}
\alpha u_{0} \int_{\Sigma} d \xi d \eta e^{-i \frac{k}{f^{\prime}}\left(x^{\prime} \xi+y^{\prime} \eta\right)} \\
\alpha u_{0} \frac{q}{2} \int_{\Sigma} d \xi d \eta e^{-i \frac{k}{f^{\prime}}\left(\left(x^{\prime}-p \frac{f^{\prime}}{k}\right) \xi+\eta y^{\prime}\right)} \\
\alpha u_{0} \frac{q}{2} \int_{\Sigma} d \xi d \eta e^{-i \frac{k}{f^{\prime}}\left(\left(x^{\prime}+p \frac{f^{\prime}}{k}\right) \xi+\eta y^{\prime}\right)}
\end{array}
\notag \]

las tres integrales son la misma, salvo un desplazamiento de \(x^{\prime}\). Sólo tenemos que hacer una. Conocemos la integral de la primera. Si etiquetamos la integral como

\[
\hat{u}_{c i r c}\left(x^{\prime}, y^{\prime}\right)=u_{0} \int_{\Sigma} d \xi d \eta e^{-i \frac{k}{f^{\prime}}\left(x^{\prime} \xi+y^{\prime} \eta\right)}
\notag \]

podemos expresar abreviadamente el resultado como

\[
\hat{u}\left(x^{\prime}, y^{\prime}\right) \propto \hat{u}_{\text {circ }}\left(x^{\prime}, y^{\prime}\right)+\frac{q}{2} \hat{u}_{c i r c}\left(x^{\prime}-p \frac{f^{\prime}}{k}, y^{\prime}\right)+\frac{q}{2} \hat{u}_{c i r c}\left(x^{\prime}+p \frac{f^{\prime}}{k}, y^{\prime}\right)
\notag \]

Figure \(\PageIndex{15}\): Aspecto en la pantalla de observación.

como se ve, cada uno de los términos tiene un peso modulado por un coeficiente, \(\frac{q}{2}\) o 1 . Podríamos ahora sustituir las funciones de BESSEL, etc.

Podemos utilizar la condición \(p \gg \frac{1}{R}\) para simplificar la forma que tendrá el módulo al cuadrado del campo (la intensidad).

\(p\) es el factor de separación de las tres funciones. Esto lo que puede suponer es que al hacer el cuadrado, los términos cruzados sean despreciables, al no solaparse las figuras de difracción dos a dos. Para verificarlo necesitamos una estimación del tamaño de la figura de difracción: usaremos el radio del primer máximo (en cuyo interior está el \(84 \%\) de la intensidad). \(r^{\prime}=1.22 \frac{\lambda f}{2 R}\). Esperamos que

\[
\frac{p f^{\prime}}{k} \gg \frac{f^{\prime}}{k R}=\frac{f^{\prime} \lambda}{2 \pi R}=\frac{1}{1.22 \pi} r^{\prime}
\notag \]

lo que, a partir de la condición que nos han dado es cierto. Por lo tanto confirmamos el que las figuras de difracción no solapan (tienen una distancia de \(\frac{p f^{\prime}}{k}\) sobre el eje \(x\) con la central).

Problema \(\PageIndex{35}\)

Se observa la figura de difracción en aproximación de FRAUNHOFER producida por una onda armónica y plana de longitud de onda \(\lambda\) que incide de forma normal sobre una rendija de anchura \(a\). Si se dobla la anchura de la rendija \(a^{\prime}=2 a, \quad \dot{c}\) cuál debería ser la longitud de onda \(\lambda^{\prime}\) para que los máximos y mínimos de difracción estuvieran en los mismos lugares?

Respuesta

Buscamos \(\lambda^{\prime}\) tal que \(a^{\prime}=2 a\). Tenemos que calcular la figura de difracción, cambiar los parámetros e imponer que máximos y mínimos estén en los mismos sitios.

\[
\begin{gathered}
\hat{u}\left(x^{\prime}\right) \propto \operatorname{sinc}\left(\frac{\pi x^{\prime} a}{\lambda f}\right) \\
\hat{u}^{\prime}\left(x^{\prime}\right) \propto \operatorname{sinc}\left(\frac{\pi x^{\prime} a^{\prime}}{\lambda^{\prime} f^{\prime}}\right)
\end{gathered}
\notag \notag \notag \]

\section{Ejercicios y problemas}

Las funciones tienen que ser iguales, salvo constante de proporcionalidad. Esto implica que los argumentos deben ser iguales.

\[
\begin{aligned}
\frac{a}{\lambda} &=\frac{a^{\prime}}{\lambda^{\prime}} \\
\lambda^{\prime} &=\frac{a^{\prime}}{a} \lambda \\
&=2 \lambda
\end{aligned}
\notag \notag \notag \]

necesitamos una onda con el doble de longitud de onda.

Problema \(\PageIndex{36}\)

Calcúlese la distancia mínima entre dos puntos de la superficie de Marte para que sus imágenes puedan resolverse por un telescopio cuya abertura es circular con diámetro \(60 \mathrm{~cm}\). Considérese que la distancia Tierra-Marte es de \(56 \times 10^{6} \mathrm{~km}\) y que la luz es monocromática con \(\lambda=560 \mathrm{~nm}\).

Respuesta

\(r^{\prime}\) es el radio del máximo central de la figura de difracción:

\[
d \geq r^{\prime}=1.22 \frac{\lambda f^{\prime}}{2 R}
\notag \]

El poder resolutivo del instrumento óptico es

\[
\frac{D}{L}=\frac{d}{f^{\prime}} \geq 1.22 \frac{\lambda}{2 R}
\notag \]

donde \(D\) es la distancia entre puntos que queremos resolver y \(L\) su distancia al instrumento. \(2 R=60 \mathrm{~cm}, L=56 \times 10^{6} \mathrm{Km}\) y \(\lambda=560 \mathrm{~nm}\). La incógnita es \(D\) en la ecuación

\[
\frac{D}{L}=1.22 \frac{\lambda}{2 R}
\notag \]

de donde \(D=63.8 \mathrm{Km}\). Los detalles deben distar entre sí más de \(64 K m\) si queremos verlos.

Problema \(\PageIndex{37}\)

Un haz plano de longitud de onda \(\lambda\) incide normalmente sobre un plano que contiene dos rendijas idénticas de anchura b separadas una distancia d. Se observa la intensidad en el plano focal imagen de una lente convergente de focal imagen \(f^{\prime}\). Delante de una de las rendijas se coloca una lámina planoparalela de espesor \(\ell\) e índice de refracción n. Considérese que la amplitud de la onda no cambia al atravesar dicha lámina. Calcúlese el punto del plano focal imagen en el que se forma el máximo de intensidad de orden \(m=0\). Estímese el orden \(m\) del máximo que tiene la mayor intensidad. Para este apartado considérese \(n=1.5\) y \(\ell=200 \lambda\).

Figure \(\PageIndex{16}\): las trayectorias que van a interferir son paralelas entre las aberturas y la lente delgada.

 

Respuesta

Parametrizaremos el punto del plano focal imagen donde \(M=0\) por \(x^{\prime}\) o \(\theta^{\prime}\).

Las dos aberturas produciran una distribución de intensidades de interferencia-difracción. El término que identificamos como interferencia es el primer factor en

\[
I\left(x^{\prime}\right) \propto(1+\cos \varphi)\left(\frac{\sin \phi}{\phi}\right)^{2}
\notag \notag \notag \]

si las intensidades son, como es el caso, iguales. \(\varphi=2 \pi M=0\) es la condición que debemos imponer sobre la variable \(\varphi\), que es la diferencia de fase entre las ondas que pasan por cada una de las rendijas.

Una forma de resolverlo es plantear la integral de \(\mathrm{FF}\), identificando la variable allí donde aparezca. Pero es más rápido calcularla directamente por métodos geométricos.

Si los ángulos son grandes, \(\tan \theta^{\prime}=\frac{x^{\prime}}{f^{\prime}}\). Si son pequeños podemos (y vamos a hacerlo) sustituir la tangente por el seno.

Como la incidencia es normal, los planos equifase son paralelos al plano de las aberturas. Al entrar una onda en el medio refractivo, la velocidad de fase de ambas ondas ya no será la misma. A partir de un plano perpendicular a las ondas planas que salen de la abertura inclinadas con ángulo \(\theta^{\prime}\) ya no hay diferencia de fase, por lo que el problema se reduce a calcular la diferencia de camino óptico entre las trayectorias que se muestran en la figura. La diferencia (camino por abajo - camino por arriba) es

\[
l+d \sin \theta^{\prime}-n l
\notag \notag \notag \]

o, en términos de fase

\[
\begin{aligned}
\varphi &=\frac{2 \pi}{\lambda}\left(d \sin \theta^{\prime}-l(n-1)\right) \\
&=0
\end{aligned}
\notag \notag \notag \]

de aquí se extrae que \(\sin \theta^{\prime}=\frac{l(n-1)}{d} \simeq \frac{x^{\prime}}{f^{\prime}}\), por lo que

\[
x^{\prime}=f^{\prime} \frac{l(n-1)}{d}
\notag \notag \notag \]

que es la solución suponiendo el ángulo \(\theta^{\prime}\) pequeño.

\section{Ejercicios y problemas}

En cuanto al orden del máximo de mayor intensidad, hay que recordar que el segundo factor

\[
I\left(x^{\prime}\right) \propto(1+\cos \varphi)\left(\frac{\sin \phi}{\phi}\right)^{2}
\notag \notag \notag \]

modula la intensidad del primero. La variable \(\phi\) es función de \(x^{\prime}\), por lo que podemos calcular el \(x^{\prime}\) para el que la difracción tiene su centro de intensidad, y de ahí pasar al número \(M\) correspondiente. En FRAUNHOFER:

\[
\phi=\frac{k x^{\prime}}{f^{\prime}} \frac{b}{2}
\notag \notag \notag \]

que tenía máximo en \(\phi=0\) o bien, \(x^{\prime}=0\) o \(\theta^{\prime}=0\). Llevándolo a

\[
\begin{aligned}
\varphi &=\frac{2 \pi}{\lambda}\left(d \frac{x^{\prime}}{f^{\prime}}-l(n-1)\right) \\
&=2 \pi M
\end{aligned}
\notag \notag \notag \]

tenemos \(M=-\frac{l(n-1)}{\lambda}=-100\).

Comentario: en todos los problemas que hemos visto hemos visto que el máximo de difracción siempre está en la dirección de incidencia del haz, pues ése es el resultado de la OG. Se puede aprovechar este resultado para decir que el máximo de difracción estará en la dirección (la normal) de incidencia del haz plano, es decir en el centro del plano focal imagen.