11.2: Otros ejercicios y problemas (por resolver)
- Page ID
- 51215
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Clasificar los cristales cuyos tensores dieléctricos son los siguientes
\[
\left(\begin{array}{lll}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 2
\end{array}\right), \quad\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right), \quad\left(\begin{array}{lll}
2 & 1 & 0 \\
1 & 1 & 0 \\
0 & 0 & 1
\end{array}\right)
\]
y hallar los ejes principales.
_________________________________________________________________
2. Una onda armónica plana se propaga en un medio uniáxico estando el eje óptico en la dirección \(z\). La fase se propaga en la dirección \(x\). Demostrar que E siempre está en el plano \(y z\). Si en \(x=0\) la onda vale \(\mathbf{E}(x=0, t)=\mathbf{E}_{0} e^{-i \omega t}\) calcular el campo en \(x=d\).
_________________________________________________________________
3. Calcular el ángulo formado por el rayo extraordinario y el ordinario que salen de la combinación de los dos prismas de la figura hechos del mismo material uniáxico, si \(\theta=15^{\circ}, n_{\mathrm{o}}=1.66 \mathrm{y} \mathrm{} n_{\mathrm{e}}=1.49\).
_________________________________________________________________
4. Un detector situado a una altura \(h\) sobre el océano recibe ondas de frecuencia \(\nu\) procedentes de una estrella lejana. Al detector llega la onda directa desde la estrella y la reflejada en la superficie del océano. Encontrar el valor de la intensidad detectada en función del ángulo \(\alpha\) que la estrella forma sobre el horizonte. Calcular al visibilidad. Por sencillez considérese que el coeficiente de reflexión \(r\) es independiente del ángulo de incidencia. Si \(\nu=10^{8} \mathrm{~Hz}, r=0.7\) y \(\alpha=45^{\circ}\) calcular el valor mínimo de \(h\) para que se tenga intensidad máxima.
_________________________________________________________________
5. Estimar el número de máximos de interferencia que hay en el máximo central de la difracción producida por dos rendijas idénticas iluminadas normalmente por un haz plano monocromático.
_________________________________________________________________
6. Calcular la posición de los máximos principales en aproximación de FRAUNHOFER para la red de la figura que está hecha de escalones de un medio transparente de índice de refracción \(n\).
_________________________________________________________________
7. Considérese la onda armónica
\[
\mathbf{E}=\mathbf{E}_{0} e^{i\left(\mathbf{k}_{c} \mathbf{r}-\omega t\right)} \notag
\]
con vector de ondas complejo \(\mathbf{k}_{c}=\mathbf{k}+i \mathbf{a}\) y con cierto vector amplitud compleja dado por \(\mathbf{E}_{0}=\alpha \mathbf{k}+\beta \mathbf{a}\), donde \(\alpha\) y \(\beta\) son escalares complejos. Esta onda se propaga en cierto medio de índice complejo \(n_{c}=n+i k\). Determinar la condición o condiciones que han de verificar \(\alpha\) y \(\beta\). Calcúlese el vector de POYNTING de esta onda.
_________________________________________________________________
8. Cierto medio dieléctrico e isótropo posee una única frecuencia de resonancia \(\omega_{0}\) :
a) ¿Es posible que siendo \(\omega_{1}<\omega_{2}\) se tenga \(\Re\{n(\omega)\}>\Re\{n(\omega)\}\)
b) En las mismas condiciones del apartado anterior: ¿para cuál de las frecuencias se tendrá una velocidad de fase mayor? (para este apartado supóngase que el medio es transparente y la onda es plana).
_________________________________________________________________
9. Considérese una onda armónica y plana que incide sobre una superficie plana que seapra dos medios transparentes e isótropos de distinto índice. El primer medio tiene índice \(n \mathrm{y}\) el segundo medio tiene índice 1. Se sabe que para incidencias desde el primer medio superiores a la del ángulo crítico (reflexión total) se produce en el segundo medio una onda cuya amplitud decrece exponencialmente con la distancia a la superficie de discontinuidad de índice. Se quiere saber en cuál de las dos situaciones siguientes el decrecimiento exponencial es mayor:
a) ángulo de incidencia próximo al ángulo crítico.
b) ángulo de incidencia próximo a \(\frac{\pi}{2}\).
Supóngase en ambos casos que la amplitud en el segundo medio sobre la superficie de discontinuidad es la misma.
_________________________________________________________________
10. Una onda armónica y plana de frecuencia \(\omega\) se propaga con vector de ondas en la dirección del eje \(Z\). Esta onda atraviesa consecutivamente tres polarizadores cuyos ejes de transmisión están en el plano \(X Y\). El primer polarizador tiene el eje de transmisión en la dirección \(X\). El eje del segundo polarizador gira a velocidad constante \(\Omega\). El eje del tercer polarizador coincide con el eje \(Y\). Se pide demostrar que tras atravesar los tres polarizadores la onda no es monocromática. Determínense las frecuencias que contiene.
_________________________________________________________________
11. Cierta onda se describe por la expresión \(\mathbf{V}(z, t)=\mathbf{V}_{0} e^{-i\left(a z^{2}+b t^{2}+2 \sqrt{a b} z t\right)}\) ¿ Es una onda plana? ¿Es armónica? ¿Cuál es la velocidad de propagación de las superficies donde \(\mathbf{V}\) toma el mismo valor?.
_________________________________________________________________
12. Cierto campo eléctrico viene dado por la expresión
\[
\mathbf{E}=\mathbf{E}_{0} \cos \left[\frac{k}{2} \mathbf{r} \cdot\left(\mathbf{u}_{1}-\mathbf{u}_{2}\right)\right] \cos \left[\omega t-\frac{k}{2} \mathbf{r} \cdot\left(\mathbf{u}_{1}+\mathbf{u}_{2}\right)\right] \notag
\]
donde \(\mathbf{u}_{1}\) y \(\mathbf{u}_{2}\) son dos vectores unitarios constantes y \(k=\frac{\omega}{c}\). Se pide:
a) ¿Es una onda armónica?.
b) Calcular su representación compleja.
c) Calcular su velocidad de fase.
d) Expresar \(\mathbf{E}(\mathbf{r}, t)\) como superposición de ondas planas.
_________________________________________________________________
13. Hállese el valor instantáneo del vector de POYNTING \(\mathbf{S}\) de la onda electromagnética en el vacío cuyo campo eléctrico viene dado por
\[
\mathbf{E}=\Re\left\{E_{0}\left(\mathbf{u}_{x}+i \mathbf{u}_{y}\right) e^{i(k z-\omega t)}\right\} \notag
\]
_________________________________________________________________
14. El campo eléctrico correspondiente a una onda plana monocromática propagándose en la dirección \(Z\) tiene la forma
\[
\mathbf{E}=A \sin (\omega t-k z) \mathbf{i}+B \cos (\omega t-k z) \mathbf{j} \notag
\]
donde \(A, B\) son constantes, con \(B>A\) e \(\mathbf{i}, \mathbf{j}\) son vectores unitarios en las direcciones \(x\) y y respectivamente. Calcúlese el promedio temporal del vector de POYNTING de dicho campo. Demuéstrese que E puede escribirse como la superposición de dos campos, uno de ellos linealmente polarizado y el otro circularmente polarizado. Escríbanse las expresiones para ambos campos.
_________________________________________________________________
15. Una onda armónica plana tiene frecuencia \(\omega\) y vector de ondas \(\mathbf{k}\) en cierto sistema de referencia. Aplicando una transformación de LORENTZ a la fase \((\mathbf{k} \cdot \mathbf{r}-\omega t)\) demostrar que la frecuencia observada en un sistema de referencia que se mueve con velocidad \(\mathbf{v}\) respecto al anterior es \(\omega^{\prime} \simeq \omega-\mathbf{k} \cdot \mathbf{v}\) si \(|\mathbf{v}| \ll c\).
_________________________________________________________________
16. Un electrón ligado se ilumina con una onda armónica plana de frecuencia \(\omega\) siendo la amplitud del campo eléctrico de \(10 \mathrm{kV} / \mathrm{m}\). La frecuencia de resonancia del electrón es \(\omega_{0}=4 \times 10^{15} \mathrm{rad} / \mathrm{s}\) y la constante de amortiguamiento es \(\gamma=10^{8} \mathrm{~Hz}\). Calcular la amplitud de oscilación del electrón y compararla con \(c\) en los casos \(\omega=5 \times 10^{15} \mathrm{rad} / \mathrm{s} \mathrm{y} \omega=\omega_{0} .\)
_________________________________________________________________
17. Comprobar que \(\epsilon_{0}\) y \(\sigma\) tienen las mismas dimensiones.
_________________________________________________________________
18. De un medio se sabe que \(\epsilon_{\text {gen }}\) es un escalar complejo que no depende del punto y que sí depende de la frecuencia. Dígase si el medio es o no es homogéneo, absorbente, conductor, dispersivo o isótropo.
_________________________________________________________________
19. En cierto medio material se propaga una onda cuya representación compleja es
\[
\mathbf{E}=\mathbf{E}_{0} e^{-\frac{3 \omega}{c} z} e^{i\left(\frac{3 \omega}{2 c} z-\omega t\right)} \notag
\]
calcular los valores de \(n\) y \(\kappa\) de dicho medio.
_________________________________________________________________
20. Sea la onda armónica inhomogénea en un medio absorbente con campo eléctrico
\[
\mathbf{E}=\mathbf{E}_{0} e^{-\mathbf{a} \cdot \mathbf{r}} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)} \notag
\]
siendo \(\mathbf{k}=b(1,0,0), \mathbf{a}=b(1,1,0)\) y \(\mathbf{E}_{0}=E_{0}(1,-1+i, d)\), donde \(b, d, E_{0}\) son constantes \(\in \Re\). Dígase si los vectores reales correspondientes a \(\mathbf{E}, \mathbf{H}\) y \(\mathbf{k}\) en \(t=0\), \(\mathbf{r}=\mathbf{0}\) son perpendiculares entre sí.
_________________________________________________________________
21. En las proximidades de una resonancia
\[
\omega^{2}-\omega_{0}^{2}=\left(\omega+\omega_{0}\right)\left(\omega-\omega_{0}\right) \simeq 2 \omega_{0}\left(\omega-\omega_{0}\right) \notag
\]
con lo que para un medio poco denso \(n\) y \(\kappa\) pueden aproximarse por
\[
\begin{aligned}
n & \simeq 1+\frac{N q^{2}}{4 m \epsilon_{0} \omega_{0}} \frac{\omega_{0}-\omega}{\left(\omega-\omega_{0}\right)^{2}+\left(\frac{\gamma}{2}\right)^{2}} \\
\kappa & \simeq \frac{N q^{2}}{8 m \epsilon_{0} \omega_{0}} \frac{\gamma}{\left(\omega-\omega_{0}\right)^{2}+\left(\frac{\gamma}{2}\right)^{2}}
\end{aligned}
\]
demostrar que los valores máximos de \(n\) y de \(\kappa\) se obtienen para \(\omega=\omega_{0}-\frac{\gamma}{2}\) y \(\omega_{0}\) respectivamente. Evaluar tales valores máximos para el caso \(N=10^{22} \mathrm{~m}^{-3}\), \(\omega_{0}=10^{16} \mathrm{rad} / \mathrm{s}\) y \(\gamma=10^{11} \mathrm{~Hz}\).
_________________________________________________________________
22. Considérese un medio poco denso cuyo índice de refracción en el visible viene determinado por una única frecuencia de resonancia en el ultravioleta. Despreciando \(\gamma\) y usando \(\omega \ll \omega_{0}\) demostrar que \(n\) puede aproximarse por \(n \simeq A+\frac{B}{\lambda^{2}}\) siendo \(A\) y \(B\) constantes \(\mathrm{y} \lambda=\frac{2 \pi c}{\omega}\).
_________________________________________________________________
23. Se tienen las mismas condiciones del problema anterior salvo que la frecuencia de resonancia \(\omega_{0}^{\prime}\) está en el infrarrojo. Demostrar que su índice de refracción en el visible, \(n^{\prime}\) puede aproximarse por \(n^{\prime} \simeq A^{\prime}-B^{\prime} \lambda^{2}\) si \(\omega \gg \omega_{0}\).
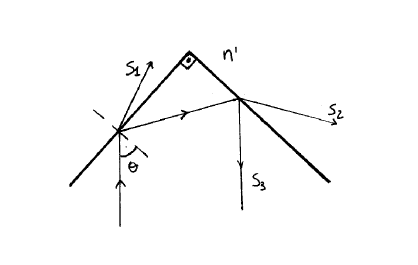
Figure \(\PageIndex{1}\): Diedro rectángulo.
_________________________________________________________________
24. Se dispone de tres medios dieléctricos cada uno de ellos con una sola resonancia situada en \(1000 \AA, 4000 \AA\) y \(8000 \AA\) respectivamente (todo lo demás se supone idéntico en los tres medios). Se quiere tener la mayor dispersión \(\frac{\mathrm{d} n}{\mathrm{~d} \omega}\) posible para \(\lambda=5000 \AA\) ¿ Cuál de los tres medios es el más adecuado?.
_________________________________________________________________
25. Aproximar el índice de refracción de un dieléctrico para frecuencias mucho mayores que cualquiera de las de resonancia.
_________________________________________________________________
26. Demostrar que la conductividad en el límite \(\omega \rightarrow 0\) vale \(\sigma \simeq \frac{N q^{2}}{m \gamma}\). Si la conductividad del cobre en tal límite es \(\sigma=5.5 \times 10^{7} \Omega^{-1} \mathrm{~m}^{-1} \mathrm{y}\) sabiendo que \(N=8 \times 10^{28} \mathrm{~m}^{-3}\) calcular \(\gamma .\)
_________________________________________________________________
27. Demostrar que si el índice de refracción del segundo medio \(\left(n^{\prime}\right)\) es menor que el del primer medio \((n)\), siendo ambos reales con \(n>n^{\prime}\) se tiene que \(t_{\|}>1\) y \(t_{\perp}>1\) para cualquier ángulo de incidencia menor que el crítico.
_________________________________________________________________
28. Consideremos un diedro rectángulo que separa dos dieléctricos de índices reales \(n\) y \(n^{\prime}\) que verifican \(\frac{n}{n^{\prime}}=\sqrt{3}\). Un haz plano linealmente polarizado con azimut \(45^{\circ}\) sufre dos reflexiones tal y como se muestra en la figura11.17. Hállense los dos valores posibles del ángulo de incidencia \(\theta\) para que el haz \(S_{3}\) esté linealmente polarizado perpendicular al plano del papel. Para cada una de las dos soluciones hállese la intensidad del haz \(S_{3}\) y también indíquese cualitativamente el tipo de polarización de los haces emergentes \(S_{1}\) y \(S_{2}\).
_________________________________________________________________
29. Una lámina planoparalela de un medio dieléctrico, isótropo y homogéneo de índice de refracción \(n_{0}\) y espesor \(d\) está en contacto con un medio metálico de constantes \(n\) y \(\kappa\). Una onda plana monocromática circularmente polarizada a derechas incide perpendicularmente desde el vacío sobre la superficie del dieléctrico, atraviesa éste, se refleja en el metal y emerge de nuevo al vacío (en sentido contrario al incidente). Determínese el estado de polarización del haz:
a) después de atravesar el dieléctrico a la ida (punto 1 de la figura).
b) después de reflejarse en el metal (punto 2 de la figura).
c) en el vacío a la vuelta (punto 3 de la figura).

_________________________________________________________________
30. Una onda armónica plana incide desde el vacío sobre la superficie plana de un medio uniáxico con ángulo de incidencia \(30^{\circ}\). El eje óptico está en el plano de incidencia y es normal a la superficie. Calcular el ángulo que forman los vectores de onda de las ondas extraordinaria y ordinaria si \(n_{o}=1.658 \mathrm{y} n_{e}=1.486\).
_________________________________________________________________
31. Se tiene un prisma \(A B C\) de material uniáxico. La luz incide normalmente a la cara \(A B\). Describir los rayos refractados por el prisma y su estado de polarización a la salida del prisma para las siguientes disposiciones del eje óptico:
a) Paralelo a las aristas.
b) Normal a la cara \(A B\).
c) Paralelo a la cara \(A B\) y normal a las aristas.
_________________________________________________________________
32. Un haz de luz linealmente polarizado pasa a través de una lámina de retardo \(\phi\) y de un polarizador. El eje óptico de la lámina est a \(45^{\circ}\) con el campo de la luz incidente y el eje de transmisión del polarizador es ortogonal al mismo. Demuéstrese que la intensidad emergente es proporcional a \(\sin ^{2}(\phi / 2)\).
_________________________________________________________________
33. Un dispositivo óptico está constituido por un polarizador ideal y una lámina cuarto de onda pegados, formando sus ejes entre sí un ángulo \(\alpha\). Sobre la cara del polarizador incide perpendicularmente un haz de luz linealmente polarizado vibrando en la dirección del eje óptico de la lámina. Se pide: (a) Calcular los semiejes y la orientación de la elipse de polarización del haz a la salida del dispositivo. (b) el valor de \(\alpha\) necesario para que la intensidad a la salida sea la misma que la incidente.
_________________________________________________________________
34. Consideremos un haz plano monocromático linealmente polarizado a \(45^{\circ}\) respecto del plano de la figura 11.19. Dicho haz incide perpendicularmente sobre una lámina planoparalela de espesor \(d_{1}\) de un medio anisótropo uniáxico con su eje óptico perpendicular a las caras. A continuación atraviesa otra lámina de espesor \(d_{2}\) del mismo material con su eje óptico paralelo a las caras y paralelo al plano del papel; \(\mathrm{y}\), por último, incide sobre una nueva lámina de espesor \(d_{3}\) del mismo material y con el eje óptico perpendicular al plano del papel. Determinar el estado de polarización a la salida cuando:
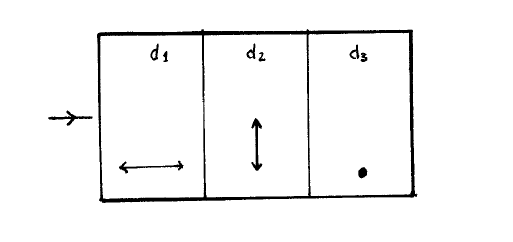
Figura \(\PageIndex{3}\): Medio anisótropo uniáxico con tres zonas.
a) \(d_{1}=d_{2}=d_{3}\)
b) \(d_{1} \neq d_{2}=d_{3}\).
_________________________________________________________________
35. Un haz de luz es mezcla de luz no polarizada y luz elípticamente polarizada. Se coloca una lámina cuarto de onda cuyos ejes coinciden con los ejes principales de la elipse de polarización de la luz. ¿Cual es la polarización de la luz a la salida de la lámina?
_________________________________________________________________
36. Dos ondas planas y monocromáticas de la misma longitud de onda inciden formando ángulos \(\alpha\) y \(-\alpha\) con la normal a una superficie que contiene una abertura cuadrada de lado \(a\). Calcular la distribución de amplitudes en el plano focal imagen de una lente.
_________________________________________________________________
37. Un sistema óptico formador de imagen puede utilizarse con luz de longitud de onda \(\lambda_{1}\) o bien con luz de longitud de onda \(\lambda_{2}\), siendo \(\lambda_{1}>\lambda_{2}\). Razónese cualitativamente con cuál de las dos longitudes de onda el poder resolutivo del instrumento es mayor.
_________________________________________________________________
38. Una red de difracción que contiene 500 rendijas por milímetro se ilumina de forma normal con una onda plana y monocromática de \(\lambda=500 \mathrm{~nm}\). Calcular los ángulos que forman con la normal a la red los máximos de orden 1 y \(2 .\)
_________________________________________________________________
39. Una red de difracción tiene un anchura de \(10 \mathrm{~cm}\). Calcular el número de rendijas necesarias y la separación entre ellas para que en el máximo de orden 1 se resuelva el doblete amarillo del sodio.
_________________________________________________________________
40. Se dispone de dos redes de difracción con 453 y 325 rendijas por milímetro respectivamente. La primera tiene una longitud de \(11.2 \mathrm{~mm}\) y la segunda \(17 \mathrm{~mm}\). ¿uál tiene mayor poder resolutivo?

