5.7: Una serie de problemas

Ahora me voy a embarcar en una serie de problemas que a primera vista pueden parecer poco relevantes para atmósferas estelares, pero se exhorta al lector a ser paciente y mirarlos, en parte porque hacen uso de muchas de las ideas encontradas hasta este punto, y también porque culminan en determinar cómo el flujo y la intensidad específica media en una atmósfera aumentan con la profundidad óptica en términos de la función fuente.

Problema 1

Una superficie que irradia un plano infinito tiene una intensidad específica uniforme (resplandor)\(I\). ¿Cuál es el flujo (irradiancia) en un punto\(\text{P}\), situado a una altura\(h\) por encima de la superficie?

Ya hemos respondido esa pregunta en la ecuación 1.15.3, y la respuesta, que, como era de esperar ya que el plano es infinito en extensión, es independiente de\(h\)\(\pi I\), es, así que sigamos con

Problema 2

Igual que el Problema 1, excepto que esta vez el espacio entre el plano radiante y el punto\(\text{P}\) se llena con un gas uniforme de coeficiente de absorción\(\alpha\). La intensidad específica (resplandor) de la superficie, se nos dice, es, siguiendo la costumbre astrofísica,\(I\). Desafortunadamente también me veré obligado a hacer uso de la “intensidad” en el sentido “estándar” del Capítulo 1, y para ello utilizaré el símbolo\(\Im\).

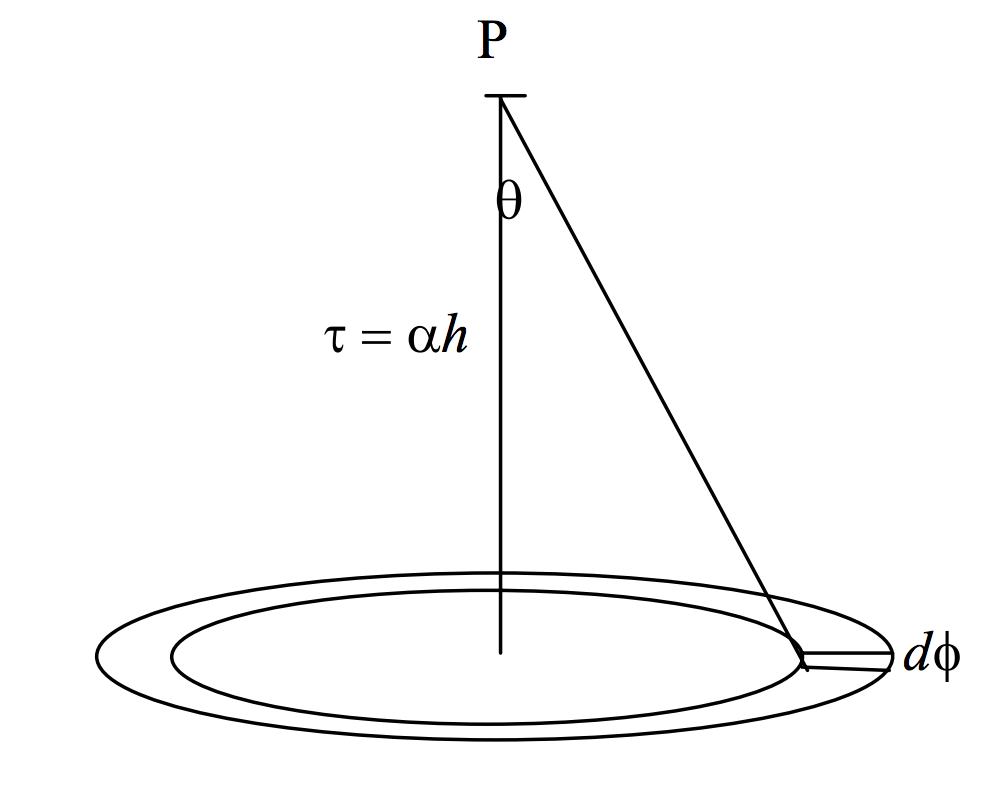
\(\text{FIGURE V.2}\)

El área elemental es\(r \ dr \ d\phi\), o, ya que\(r = h \tan \theta\), lo es\(h^2 \tan \theta \sec^2 \theta d\theta d\phi\). La intensidad del área elemental hacia\(\text{P}\) es la intensidad específica (resplandor) multiplicada por el área proyectada:

\[d\Im = Ih^2\tan \theta \sec^2 \theta \ d\phi \ \cos\theta\]

Si no hubiera absorción, la irradiancia de\(\text{P}\) por el área elemental sería

\[d\Im \cos \theta / (h^2 \sec^2 \theta),\]

que se convierte\[I \sin \theta \cos \theta \ d \theta \ d \phi .\]

Pero se reduce por absorción por un factor\(e^{−\tau \sec \theta}\), donde\(\tau = \alpha h\). Por lo tanto, la irradiancia de\(\text{P}\) por el área elemental es

\[Ie^{-\tau \sec \theta} \sin \theta \cos \theta \ d\theta \ d \phi .\]

Para la irradiancia a\(\text{P}\) (o “flujo” en el sentido astrofísico) por todo el plano infinito integramos desde\(\phi = 0\) hacia\(2\pi\) y\(\theta = 0\) hacia\(\pi/2\), para obtener

\[2\pi I \int_0^{\pi/2} e^{-\tau \sec \theta} \sin \theta \cos \theta d\theta\]

Si ahora escribimos\(x = \sec \theta\), esto se convierte

\[\text{Irradiance at P} = 2\pi I E_3 (\tau),\]

y esperamos que el lector no haya olvidado el significado de\(E_3\) -si se tiene, como diría el juego de serpientes y escaleras, Volver al Capítulo 3. Tenga en cuenta que, al\(\tau = 0\), esto se convierte\(\pi I\), como se esperaba.

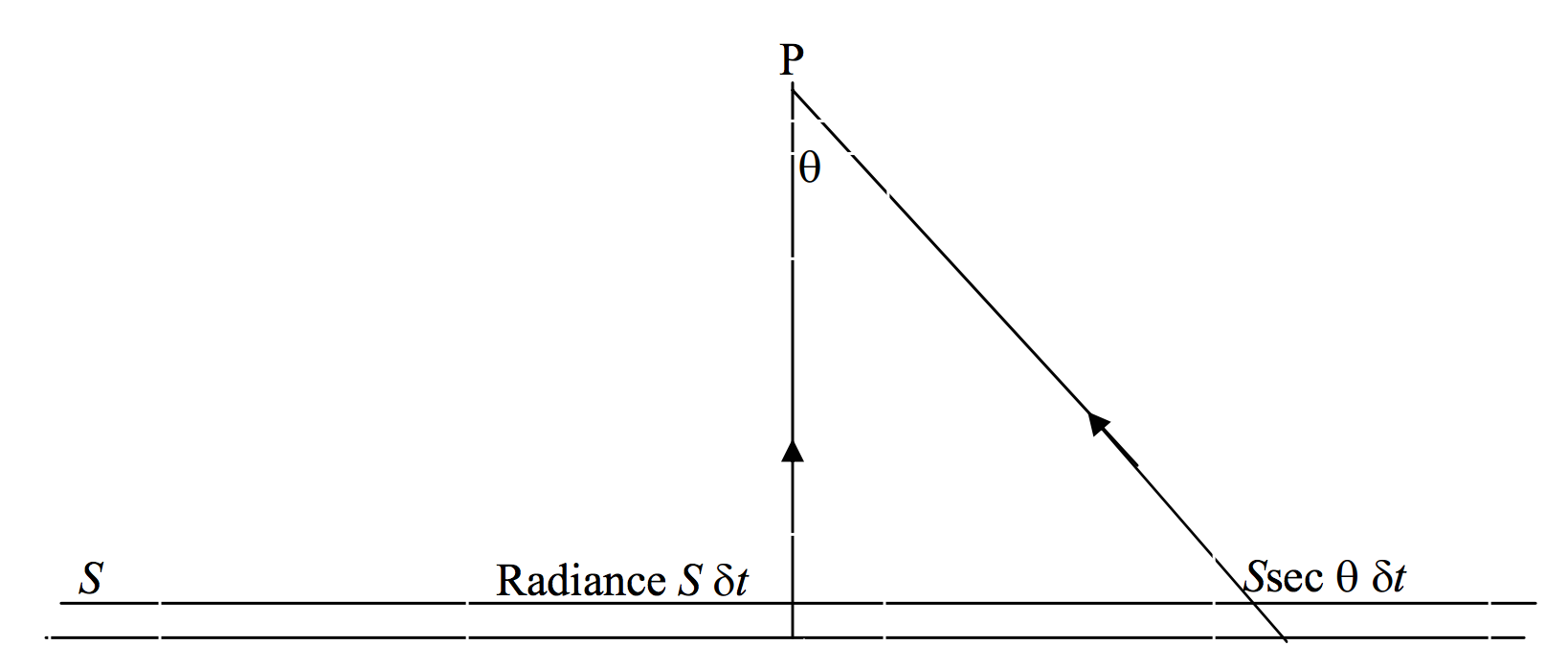
\(\text{FIGURE V.3}\)

Un punto\(\text{P}\) está situado a una altura\(h\) por encima de una porción plana infinita de gas de espesor óptico\(\delta \tau\) y función de fuente\(S\). No hay nada entre\(\text{P}\) y la rodaja de gas. ¿Cuál es el flujo (irradiancia) en\(\text{P}\)?

A primera vista esto parece ser idéntico al Problema 1, excepto que la intensidad específica de la rebanada es\(S\delta t\). Sin embargo, una mirada más cuidadosa al diagrama revelará que la intensidad específica de la rebanada no es de ninguna manera uniforme. Es más oscuro directamente debajo\(\text{P}\), y, cuando\(\text{P}\) mira más lejos de su nadir, la rebanada se vuelve cada vez más brillante, estando\(S \ \sec \theta \ \delta t\) en ángulo\(\theta\). El flujo ascendente (“irradiancia”) en\(\text{P}\) es por lo tanto

\[F_+ = 2 \pi S \delta t \int_0^{\pi/2} \sec \theta \cos \theta \sin \theta \ d\theta = 2\pi S \delta t\]

Igual que el Problema 3, excepto que esta vez colocaremos un gas absorbente de espesor óptico\(t\) entre\(\text{P}\) y la rebanada\(\delta t\).

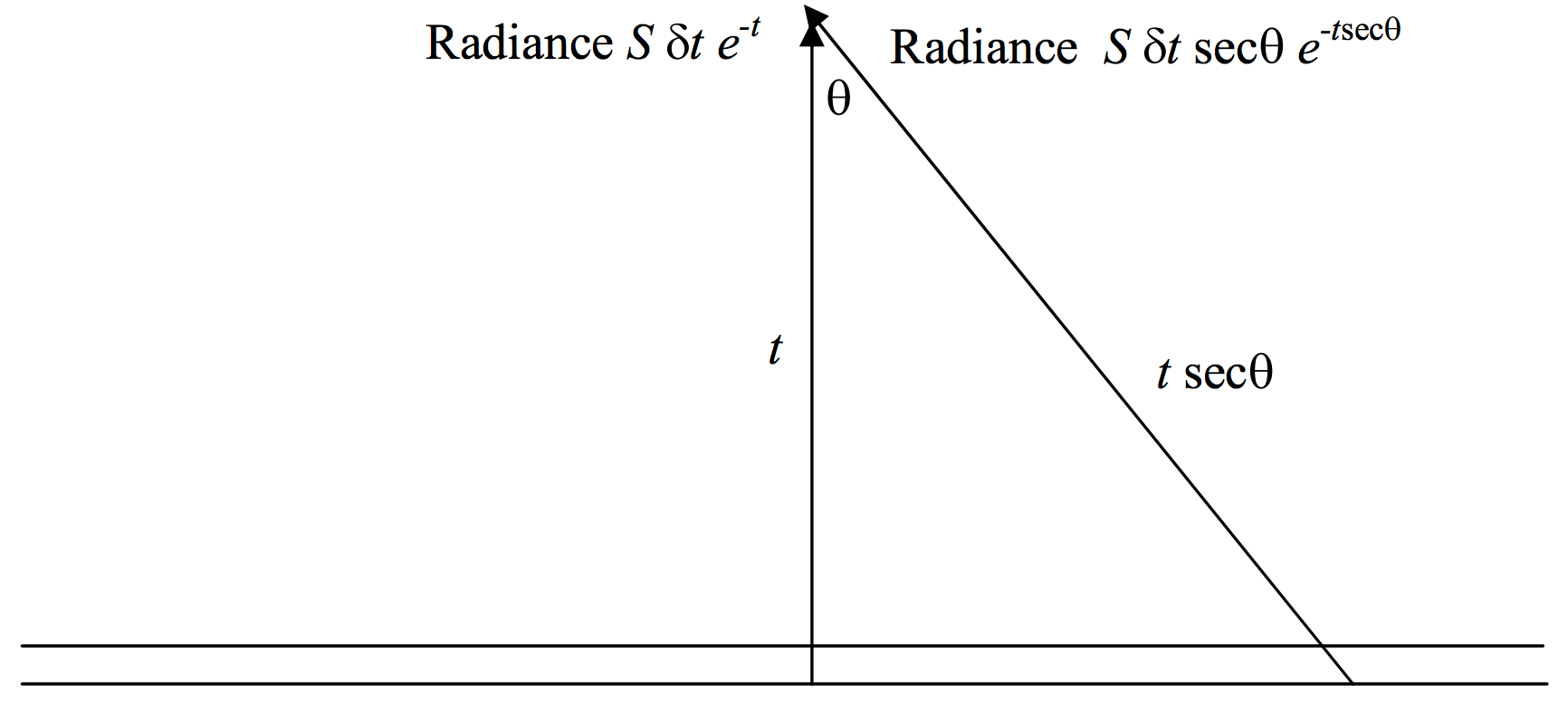
\(\text{FIGURE V.4}\)

En ese caso, el flujo (irradiancia) a\(\text{P}\) partir de un elemento en un ángulo\(\theta\) se reduce\(e^{-t \sec \theta}\) y, en consecuencia, el flujo a\(\text{P}\) partir de toda la rebanada es

\[F_+ = 2\pi S \delta t \int_0^{\pi/2} \sec \theta \cos \theta \sin \theta \ d\theta = 2\pi S \delta t .\]

Si escribimos\(x = \sec \theta\), muy pronto veremos que esto es

\[\text{Flux (irradiance) at P} = 2\pi S \delta t E_2 (t)\]

Problema 5 (un resultado importante en la teoría de la atmósfera)

Ahora considere un punto\(\text{P}\) a una profundidad óptica\(\tau\) en una atmósfera estelar. (El uso de la palabra “profundidad” implicará que\(\tau\) se mide hacia abajo desde la superficie hacia el centro de la estrella.) Asumiremos una atmósfera paralela plana es decir, una atmósfera poco profunda, o una que sea poco profunda en comparación con el radio de la estrella, o no vamos a adentrarnos muy profundamente en la atmósfera. El punto\(\text{P}\) está incrustado en un gas absorbente, dispersante y emisor. El flujo que sube desde abajo es igual a las contribuciones de todas las rebanadas debajo\(\text{P}\), de\(t = \tau\) a\(t = \infty\):

\[F_+ = 2\pi \int_\tau^\infty S(t) E_2 (t-\tau) dt \]

El flujo que se derrite desde arriba es el aporte de todas las rebanadas de arriba, desde\(t = 0\) hasta\(t = \tau\):

\[F_- = 2\pi \int_0^\tau S(t) E_2 (\tau - t) dt\]

El flujo ascendente neto en un punto\(\text{P}\) a una profundidad óptica\(\tau\) en una atmósfera absorbente, dispersante y emisora es

\[F(\tau) = 2\pi \left[ \int_\tau^\infty S(t) E_2 (t-\tau) dt - \int_0^\tau S(t) E_2 (\tau-t)dt \right] \label{5.7.1} \tag{5.7.1}\]

La integral\(H\) es solo\(1/(4\pi)\) veces esto.

Ahora se le pide al lector que encuentre las integrales\(J(\tau)\) y\(K\tau)\). Estos deben darse en forma de integrales que incluyan una función fuente\(S(t)\) y una función integral exponencial\(E(t − \tau)\) o\(E(\tau − t)\). Es importante obtener el argumento de la manera correcta. Un camino es correcto; el otro está mal.

Problema 6

Este es un problema más fácil, aunque el resultado es importante.

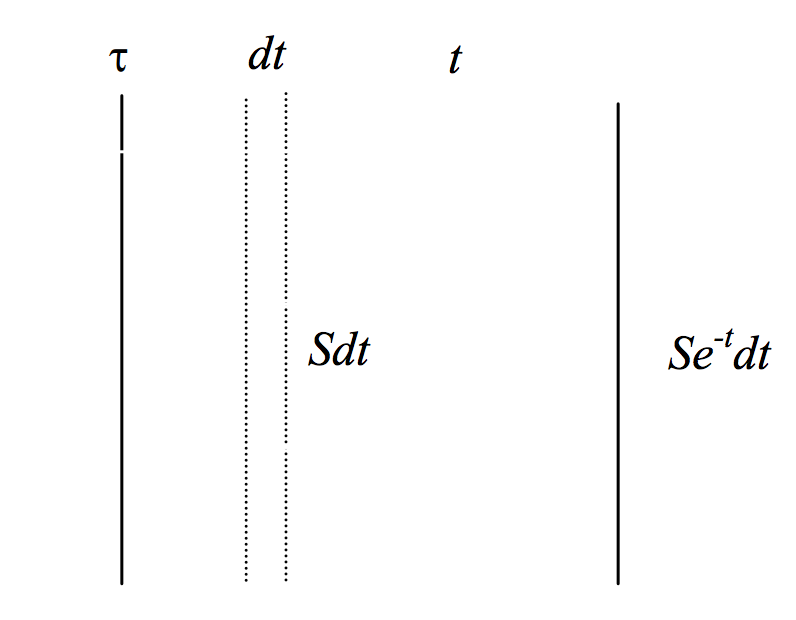
\(\text{FIGURE V.5}\)

La Figura V.5 muestra una losa de gas de espesor óptico\(\tau\). Se supone que el observador está a la derecha de la losa, y la profundidad óptica se mide desde la cara derecha de la losa hacia la izquierda. A una profundidad óptica\(t\) dentro de la losa hay una rebanada de espesor óptico\(dt\). Se supone que la losa tiene una función de origen uniforme\(S\) en todas partes. La función de origen es la intensidad específica por unidad de espesor óptico, por lo que la intensidad específica de la rebanada es\(Sdt\). La intensidad emergente de esta rebanada, en el momento en que alcanza la superficie derecha de la losa, es\(Se^{-t} dt\). La intensidad específica emergente de toda la losa es la suma de las contribuciones de todas esas rebanadas a lo largo de la losa; es decir\(\int_0^\tau Se^{-t}dt\). Si la función de origen es uniforme a lo largo de la losa, por lo que no\(S\) es una función de\(t\), encontramos que la intensidad específica emergente de la losa es

\[I = S \left( 1-e^{-t} \right) \label{5.7.2} \tag{5.7.2}\]

Problema. Una cantidad de gas caliente se mantiene en una caja de 50 cm de largo. El coeficiente de emisión del gas es\(0.06 \ \text{W sr}^{−1} \text {m}^{−3}\) y el coeficiente de extinción es\(0.025 \ \text{cm}^{−1}\). ¿Cuál es la intensidad específica emergente (resplandor)? (Yo lo hago\(1.71 \times 10^{−2} \text{W m}^{−2} \text{sr}^{−1}\).)