7.21: Efecto Zeeman

Cuando un gas caliente que está emitiendo o absorbiendo líneas espectrales se coloca en un campo magnético, las líneas se dividen en varios componentes. Esto se conoce como el efecto Zeeman, descubierto en 1896 por el espectroscopista holandés P. Zeeman.

Si empezamos pensando en un átomo con cero espín nuclear, se recordará que cada nivel de energía excepto los que tienen\(J = 0\) es degenerado. Es decir, hay\(2J + 1\) ondulaciones, o estados propios, o simplemente estados, cada uno descrito por un número cuántico\(M\), que va de\(−J\) a\(+J\), y cada uno de estos estados tiene exactamente la misma energía. Cuando el átomo se coloca en un campo magnético externo, esta degeneración se elimina, y cada estado tiene una energía ligeramente diferente. Esto sucede a ambos niveles involucrados en la formación de una línea (a menos que uno de los niveles tenga\(J = 0\)), con el resultado de que la línea que une los dos niveles se divide en una serie de componentes. Se recordará que una línea une dos niveles. De manera similar un componente (Zeeman) une dos estados. Así como un multiplete es la totalidad de líneas que unen dos términos, así una línea es la totalidad de componentes que unen dos niveles. En ausencia de un campo magnético, todos los estados dentro de un nivel tienen la misma energía, y todos los componentes que componen una línea tienen la misma longitud de onda. Un término es descrito por\(LS\). Su multiplicidad es\(2 \text{min} \left\{ L , S \right\} +1\) y su peso estadístico es\((2L +1)( 2S +1)\). Un nivel es descrito por\(LSJ\). Su degeneración y peso estadístico son\(2J + 1\). Un estado es descrito por\(LSJM\). No es degenerado; su peso estadístico lo es\(1\).

En las secciones 9 ,10, y 11 de este capítulo, me metí en algún problema para persuadirte de que un electrón no es una esfera dura, giratoria que se mueve en órbita circular alrededor de un núcleo. Más bien describí los electrones en términos de funciones de onda que describen la amplitud de probabilidad, y los números cuánticos eran valores propios de ciertos operadores y estaban restringidos a ciertos valores como resultado de condiciones límite. El modelo que usamos para describir el comportamiento de los átomos depende de nuestro propósito y, si nuestro propósito fuera obtener experiencia en las complejidades de los cálculos mecánicos cuánticos, tendríamos que involucrarnos fuertemente en el álgebra de kets, operadores y funciones propias. Nuestro propósito actual, sin embargo, es conocer de manera bastante descriptiva la espectroscopia y describir los fenómenos Zeeman sin la intención de realizar cálculos mecánicos cuánticos. Será conveniente volver a un modelo de un electrón, si no como una partícula dura, giratoria, orbitante, al menos como una entidad que posee los atributos de momento angular orbital y de giro y consecuentemente también de momento magnético.

En particular, recordamos que un electrón en órbita tiene un momento angular orbital\(\sqrt{l(l +1)}\hbar\), donde\(\hbar=h/(2\pi )\) tiene el valor\(1.055 \times 10^{−34} \text{J s}\). Ahora bien, si tomamos la relación magnetogírica de un electrón en órbita para ser\(e/ (2m)\), el momento magnético de un electrón en órbita es\(\sqrt{l(l+1)}\cdot \dfrac{e \hbar}{2m}\). (Quienes se oponen a este sencillo tratamiento -y hay algunas objeciones bastante obvias- no tendrán otra alternativa que hacer una correcta derivación mecánica cuántica, aunque el resultado sea el mismo). En cualquier caso, la cantidad\(\dfrac{e\hbar}{2m}\), una unidad de momento magnético, se llama el magnetón Bohr, y su valor es\(9.274 \times 10^{−24} \ \text{N m T}^{−1}\) o\(\text{A m}^2\). Utilizaré el símbolo\(\mu_B\) para indicar el magnetón Bohr. Así el momento angular orbital de un electrón es\(\sqrt{l(l +1)}\hbar\) y su momento magnético es\(\sqrt{l(l+1)}\mu_B\) La relación magnetogírica de un electrón en órbita (sin tener en cuenta la contribución al momento angular y momento magnético de su giro) es\(\mu_B / \hbar = e/ (2m) = 8.794 \times 10^{10} \ \text{C kg}^{-1}\), o, si acordamos expresar momento angular en unidades de\(\hbar\) y momento magnético en unidades de magnetones Bohr, la relación magnetogírica de un electrón en órbita (aún sin tener en cuenta las contribuciones del espín) es\(1\). El momento angular de espín de un electrón es\(\sqrt{s(s+1)}\hbar\)\(s =1/2\), dónde, y su momento magnético es (muy cercano a)\(2\sqrt{s(s+1)}\hbar\), de manera que su relación magnetogírica es justa\(e/m\), o, en unidades de\(\mu\) y\(\hbar\), es\(2\). (El valor exacto de la relación magnetogírica, en unidades de\(\mu_B / \hbar\), es un poco más que\(2\), y es una de las constantes físicas fundamentales más precisamente conocidas. Su valor en el año 2000 se da como 2.002 319 304 374.)

En la discusión del efecto Zeeman, necesitaremos conocer la relación magnetogírica del átomo en un nivel dado, ya que esto determina la forma en que los niveles se dividen en un campo magnético. La relación entre el momento magnético en unidades de\(\mu_B\) y el momento angular en unidades de\(\hbar\) se conoce como factor de división de Landé, y generalmente se denota con el símbolo\(g\). Es la relación magnetogírica en unidades de\(e/(2m)\), o\(8.794 \times 10^{10} \ \text{C kg}^{-1}\). La relación magnetogírica, o factor de división Landé, de un átomo en un nivel dado depende del ángulo entre los vectores\(\textbf{L}\)\(\textbf{S}\) y y por lo tanto de su resultante\(\textbf{J}\), y, aunque no lo hago aquí, no es difícil demostrar que, en el caso de\(LS\) -acoplamiento, el Landé factor de división tiene el valor

\[g = 1 + \dfrac{J(J+1) + S(S+1) - L(L+1)}{2J(J+1)}. \label{7.21.1} \tag{7.21.1}\]

(Esta fórmula se calcula utilizando el valor aproximado\(2\) para la relación magnetogírica del electrón en lugar de la más precisa\(2.00232\). Con mayor precisión, debería escribirse

\[g = 1 + 1.00232 \dfrac{J(J+1)+S(S+1)-L(L+1)}{2J(J+1)}. \label{7.21.2} \tag{7.21.2}\]

Están disponibles fórmulas para el\(g\) factor -para otros esquemas de acoplamiento, pero no las doy aquí, ya que en la práctica el acoplamiento entre momentos angulares de electrones en átomos complejos suele ser intermedio entre extremos idealizados, y el cálculo tiene que hacerse numéricamente. En muchos de los átomos más ligeros, sin embargo, el\(LS\) acoplamiento puro es una buena aproximación. El\(g\) -valor se puede encontrar experimentalmente a partir de observaciones del efecto Zeeman, y, además de la regla de intervalo de Landé mencionada anteriormente, esto proporciona otra buena indicación de lo cerca que está un nivel al\(LS\) acoplamiento.

Problema. La\(^5 \text{P}_1 - \ ^5 \text{D}_0^\text{o}\) línea de\(\text{Fe}_\text{ I}\) at\(617.33 \ \text{nm}\) se utiliza a menudo para investigar los campos magnéticos en las manchas solares. La línea más fuerte del multiplete que incluye esta línea es\(^5\text{P}_3 - \ ^5 \text{D}_4^\text{o}\). Calcular el\(g\) factor -para cada uno de los cuatro niveles mencionados.

Un pequeño punto a hacer es el siguiente. Por lo que hemos dicho, el momento magnético de un átomo (excluyendo el espín nuclear, si lo hay) es de magnitud\(\mu = g\mu_B \sqrt{J (J +1)}\). (Esto se desprende de la definición de\(g\), que es la relación del momento magnético en unidades del magnetón Bohr - es decir,\(\mu/\mu_B\) - al momento angular en unidades de\(\hbar\).) En forma vectorial esto debe escribirse\(\boldsymbol{\mu} = −g \mu_B \textbf{J}\), donde\(\textbf{J}\) es un vector adimensional de magnitud\(\sqrt{J(J +1)}\) y el signo menos surge debido a la carga electrónica negativa, siendo los vectores de momento magnético y momento angular dirigidos opositivamente.

Cuando se investigó por primera vez el efecto Zeeman, se observó que las líneas se dividían en solo tres componentes, y esto se denominó el efecto Zeeman normal. Posteriormente, se observaron patrones más complejos, y esto se denominó el efecto anómalo de Zeeman. Tal y como ahora lo entendemos, el llamado efecto Zeeman “normal” es meramente el efecto Zeeman observado en líneas que unen niveles con giro\(S = 0\), que tienen un patrón Zeeman más simple que otras líneas. Además del experimento Stern-Gerlach, fue el estudio de la división “anómala” de Zeeman lo que dio lugar al descubrimiento del espín electrónico.

Ahora estamos en condiciones de comenzar a mirar cómo se dividen los niveles de energía en presencia de un campo magnético. Consideremos, por ejemplo, un\(^1 \text{P}_1\) level (\(L, \ S, \ J = 1, 0, 1\)). El factor Landé es\(1\). (Obsérvese que para cualquier nivel en el que S = 0 y por lo tanto en el que\(J\) y\(L\) sean necesariamente iguales, Ecuación\(\ref{7.21.1}\) (o\ ref {7.21.2}) lo demuestra\(g = 1\).)

El momento magnético es\(\boldsymbol{\mu} = −g \mu_B \textbf{J} = −\mu_B \textbf{J}\). La energía de un imán es un campo magnético es\(−\boldsymbol{\mu} \cdot \textbf{B}\), así que en este caso lo es\(\mu_B \textbf{J}\cdot \textbf{B}\). Pero\(\textbf{J}\cdot \textbf{B}\) es igual a\(B\) veces el componente de\(\textbf{J}\) en la dirección de\(\textbf{B}\), que es\(M\). Así es la energía del estado\(M\) en el campo magnético\(\mu_B MB\). Hay tres valores de\(M \ (−1, \ 0, \ 1)\). La división del nivel en sus tres estados es linealmente proporcional al campo magnético\(B\), y la separación entre estados adyacentes es\(\mu_B B\).

Si consideramos un\(^1 \text{D}_2\) nivel, nuevamente\(g = 1\), y los estados tienen justamente el mismo espaciado, salvo que esta vez hay cinco estados, con\(M = −2 \) a\(+2\).

Ahora considera la línea\(^1 \text{P}_1 − \ ^1 \text{D}_2\). Esta es la totalidad de todas las transiciones que conectan los tres estados en el uno a los cinco estados en el otro. No todas las transiciones son posibles, sin embargo, por lo que no hay quince componentes a la línea. Las reglas de selección (a tratar en la Sección 7.24) limitan las únicas transiciones posibles a aquellas para las cuales\(\Delta M = 0\) o\(\pm 1\). La Figura VII.1 muestra los niveles de energía de los ocho estados y las nueve posibles transiciones que los conectan.

Se verá que los nueve componentes están en tres grupos de tres, y que, debido a que los espaciamientos en los dos niveles son los mismos (lo que a su vez es resultado de\(S = 0\)), las tres líneas de un grupo dado tienen exactamente la misma longitud de onda (aunque las he dibujado ligeramente separadas). En consecuencia, verás en el espectro aparentemente solo tres componentes Zeeman, el completo

\(\text{FIGURE VII.1}\)

nueve no estando completamente separados. Esto es lo que se llamó el efecto Zeeman “normal”. No obstante, en cuanto\(S \neq 0\), los\(g\) -valores de los dos niveles serán diferentes, los espaciamientos de los estados en los dos niveles serán diferentes, todos los componentes estarán completamente separados, y vemos el efecto Zeeman “anómalo”, aunque no hay nada realmente anómalo al respecto. En cierto sentido, el efecto Zeeman “normal” es excepcional. En la figura\(\text{VII.2}\) he dibujado, esquemáticamente (con longitud de onda aumentando linealmente hacia la derecha), el patrón Zeeman para\(^2 \text{S}_{\dfrac{1}{2}} - \ ^2 \text{P}_{\dfrac{3}{2}}\). Los factores de división para los\(\text{S}\) niveles\(\text{P}\) y son, respectivamente,\(2\) y\(4/3\). Sucede que en este caso los seis componentes Zeeman están igualmente espaciados, aunque no siempre es así; el patrón exacto de los componentes Zeeman varía de línea a línea

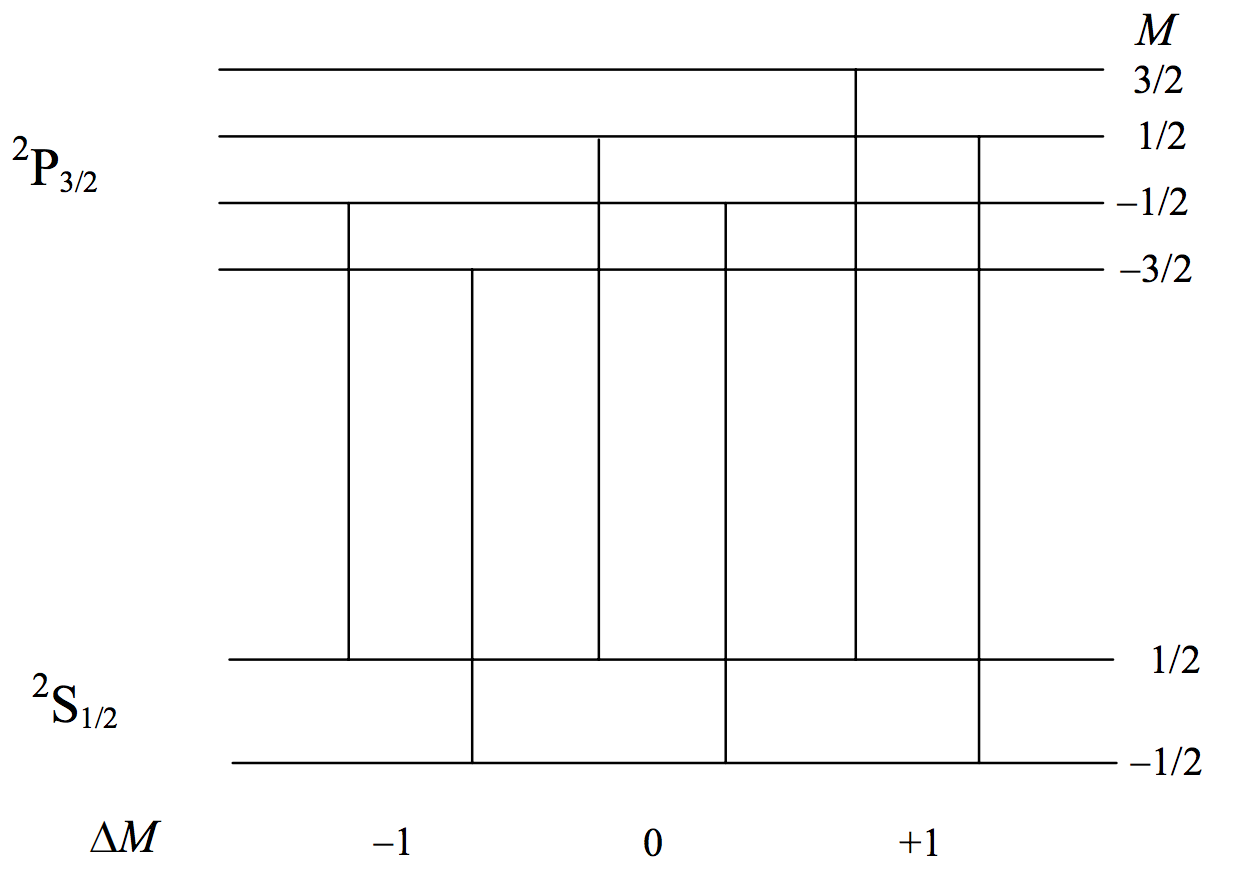
\(\text{FIGURE VII.2}\)