8.4: Propiedades magnéticas y el efecto Zeeman

El magnetismo es el resultado del movimiento circular de las partículas cargadas. Esta propiedad se demuestra a escala macroscópica haciendo un electroimán a partir de una bobina de alambre y una batería. Los electrones que se mueven a través de la bobina producen un campo magnético (Figura\(\PageIndex{1}\)), que se puede considerar que se origina en un dipolo magnético o un imán de barra.

Figura\(\PageIndex{1}\): Aparato de Faraday para demostrar que un campo magnético puede producir una corriente. Un cambio en el campo producido por la bobina superior induce una emf y, por lo tanto, una corriente en la bobina inferior. Cuando se abre y cierra el interruptor, el galvanómetro registra las corrientes en direcciones opuestas. No fluye corriente a través del galvanómetro cuando el interruptor permanece cerrado o abierto. (CC BY 3.0; OpenStax).

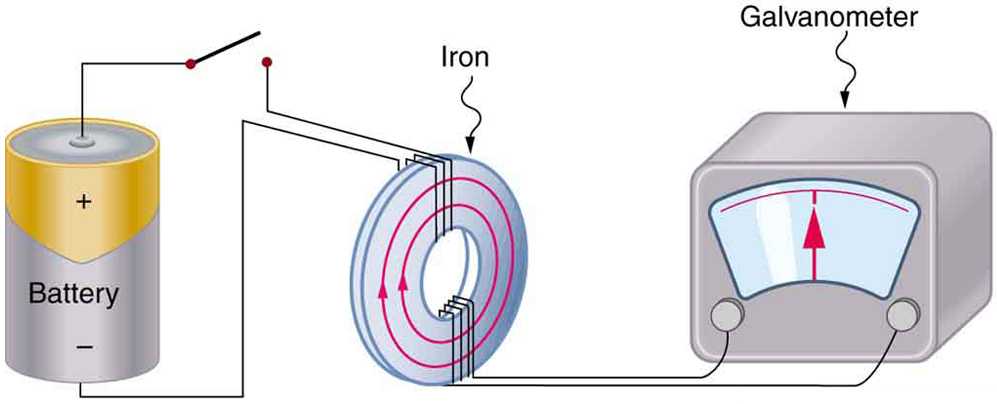
El magnetismo es el resultado del movimiento circular de las partículas cargadas.

Los electrones en los átomos también están moviendo cargas con momento angular por lo que ellos también producen un dipolo magnético, razón por la cual algunos materiales son magnéticos. Un dipolo magnético interactúa con un campo magnético aplicado, y la energía de esta interacción viene dada por el producto escalar del momento dipolo magnético, y el campo magnético,\(\vec{B}\).

\[E_B = - \vec{\mu} _m \cdot \vec{B} \label {8.4.1}\]

Los imanes son accionados por fuerzas y pares cuando se colocan dentro de un campo magnético externo aplicado (Figura\(\PageIndex{2}\)). En un campo externo uniforme, un imán no experimenta fuerza neta, sino un par neto. El par intenta alinear el momento magnético (\(\vec{\mu} _m\)del imán con el campo externo\(\vec{B}\). El momento magnético de un imán apunta desde su polo sur hasta su polo norte.

Figura\(\PageIndex{2}\): Un imán sentirá una fuerza para realinearse en un campo externo, es decir, pasar de una energía mayor a una energía más baja. La energía de este sistema está determinada por la Ecuación\ ref {8.4.1} y la clásica puede variar ya que el ángulo entre\(\vec{\mu} _m\) y\(\vec{B}\) puede variar continuamente de 0 (baja energía) a 180° (alta energía).

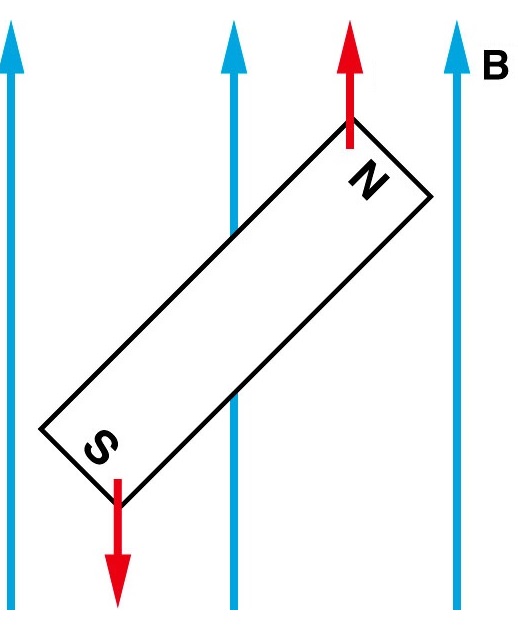
En un campo magnético no uniforme, un bucle de corriente, y por lo tanto un imán, experimenta una fuerza neta, que intenta tirar de un dipolo alineado hacia regiones donde la magnitud del campo magnético es mayor y empujar un dipolo antialineado hacia regiones donde la magnitud del campo magnético es menor.

Efectos cuánticos

Como era de esperar, el panorama cuántico es diferente. Pieter Zeeman fue uno de los primeros en observar las divisiones de líneas espectrales en un campo magnético causado por esta interacción. En consecuencia, tales divisiones se conocen como el efecto Zeeman. Ahora usemos nuestro conocimiento actual para predecir cómo sería el efecto Zeeman para la transición de 2p a 1s en hidrógeno, y luego comparemos esta predicción con una teoría más completa. Para entender el efecto Zeeman, que utiliza un campo magnético para eliminar la degeneración de diferentes estados de momento angulares, necesitamos examinar cómo un electrón en un átomo de hidrógeno interactúa con un campo magnético externo,\(\vec{B}\). Dado que el magnetismo es el resultado del movimiento circular de las partículas cargadas, debemos buscar una relación entre el momento angular\(\vec{L}\) y el momento dipolar magnético\(\vec{\mu} _m\).

La relación entre el momento dipolo magnético\(\vec{\mu} _m\) (también denominado simplemente el momento magnético) y el momento angular\(\vec{L}\) de una partícula con masa m y carga\(q\) viene dada por

\[ \vec{\mu} _m = \dfrac {q}{2m} \vec{L} \label {8.4.2}\]

Para un electrón, esta ecuación se convierte

\[ \vec{\mu} _m = - \dfrac {e}{2m_e} \vec{L} \label {8.4.3}\]

donde la carga específica y la masa del electrón han sido sustituidas por\(q\) y\(m\). El momento magnético para el electrón es un vector que apunta en la dirección opuesta a\(\vec{L}\), ambos clásicamente son perpendiculares al plano del movimiento de rotación.

Ejercicio\(\PageIndex{1}\)

¿Un electrón en el estado fundamental del hidrógeno tendrá un momento magnético? ¿Por qué o por qué no?

La relación entre el momento angular de una partícula y su momento magnético se expresa comúnmente como una relación, llamada relación giromagnética,\(\gamma\). El giroscopio es griego para giro, por lo que el giromagnético simplemente relaciona el giro (momento angular) con el magnetismo. Ahora también sabes por qué los sándwiches griegos hechos con carne cortada de un asador volteando un fuego se llaman giroscopios.

\[ \gamma = \dfrac {\mu _m}{L} = \dfrac {q}{2m} \label {8.4.4}\]

En el caso específico de un electrón,

\[ \gamma _e = - \dfrac {e}{2m_e} \label {8.4.5}\]

Ejercicio\(\PageIndex{2}\)

Calcular la magnitud de la relación giromagnética para un electrón.

Para determinar la energía de un átomo de hidrógeno en un campo magnético necesitamos incluir la forma operadora del átomo de hidrógeno Hamiltoniano. El hamiltoniano siempre consiste en todos los términos energéticos que son relevantes para el problema que nos ocupa.

\[ \hat {H} = \hat {H} ^0 + \hat {H} _m \label {8.4.6}\]

donde\(\hat {H} ^0\) está el operador hamiltoniano en ausencia del campo y\(\hat {H} _m\) se escribe utilizando las formas operadoras de Ecuaciones\(\ref{8.4.1}\) y\(\ref{8.4.3}\)),

\[ \hat {H}_m = - \hat {\mu} \cdot \vec{B} = \dfrac {e}{2m_e} \hat {L} \cdot B \label {8.4.7}\]

El producto escalar

\[ \hat {L} \cdot \vec{B} = \hat {L}_x B_x + \hat {L}_y B_y + \hat {L}_z B_z \label {8.4.8}\]

simplifica si el eje z se define como la dirección del campo externo porque entonces\(B_x\) y\(B_y\) son automáticamente 0, y la ecuación\ ref {8.4.6} se convierte

\[ \hat {H} = \hat {H}^0 + \dfrac {eB_z}{2m_e} \hat {L} _z \label {8.4.9}\]

donde\(B_z\) está la magnitud del campo magnético, que está a lo largo del eje z.

Ahora podemos preguntarnos: “¿Cuál es el efecto de un campo magnético en la energía de los orbitales de los átomos de hidrógeno?” Para responder a esta pregunta, no volveremos a resolver la ecuación de Schrödinger; simplemente calculamos el valor esperado de la energía,\(\left \langle E \right \rangle \), utilizando las funciones de onda de átomos de hidrógeno existentes y el nuevo operador hamiltoniano.

\[ \left \langle E \right \rangle = \left \langle \hat {H}^0 \right \rangle + \dfrac {eB_z}{2m_e} \left \langle \hat {L} _z \right \rangle \label {8.4.10}\]

donde

\[\left \langle \hat {H}^0 \right \rangle = \int \psi ^*_{n,l,m_l} \hat {H}^0 \psi _{n,l,m_l} d \tau = E_n \label {8.4.11}\]

y

\[\left \langle \hat {L}_z \right \rangle = \int \psi ^*_{n,l,m_l} \hat {L}_z \psi _{n,l,m_l} d \tau = m_l \hbar \label {8.4.12}\]

Ejercicio\(\PageIndex{3}\)

Demostrar que el valor de expectativa\(\left \langle \hat {L}_z \right \rangle = m_l \hbar\).

El enfoque del valor de expectativa proporciona un resultado exacto en este caso porque las funciones de onda del átomo de hidrógeno son funciones propias de ambos\(\hat {H} ^0\) y\(\hat {L}_z\). Si las funciones de onda no fueran funciones propias del operador asociadas con el campo magnético, entonces este enfoque proporcionaría una estimación de primer orden de la energía. Las estimaciones de primer orden y de orden superior de la energía son parte de un enfoque general para desarrollar soluciones aproximadas a la ecuación de Schrödinger. Este enfoque, llamado teoría de la perturbación, se discute en el siguiente capítulo.

El valor de expectativa calculado para la energía total en este caso es la suma de la energía en ausencia del campo\(E_n\), más la energía Zeeman,\(\dfrac {e \hbar B_z m_l}{2m_e}\)

\[\begin{align} \left \langle E \right \rangle &= E_n + \dfrac {e \hbar B_z m_l}{2m_e} \\[4pt] &= E_n + \mu _B B_z m_l \label {8.4.13} \end{align}\]

El factor

\[ \dfrac {e \hbar}{2m_e} = - \gamma _e \hbar = \mu _B \label {8.4.14}\]

define la constante\(\mu _B\), llamada magnetón Bohr, que se toma como el momento magnético fundamental. Cuenta con unidades de\(9.2732 \times 10^{-21}\) ERG-Gauss o\(9.2732 \times 10^{-24}\) Joule/Tesla. Este factor te ayudará a relacionar los campos magnéticos, medidos en Gauss o Tesla, con energías, medidas en ergs o julios, para cualquier partícula con una carga y masa igual que un electrón.

La ecuación\ ref {8.4.13} muestra que la degeneración numérica\(m_l\) cuántica del átomo de hidrógeno es eliminada por el campo magnético. Por ejemplo, los tres estados\(\psi _{211}\),\(\psi _{21-1}\), y\(\psi _{210}\), que están degenerados en campo cero, tienen diferentes energías en un campo magnético, como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): El efecto Zeeman. La emisión cuando un electrón cambia de un orbital 2p a un orbital 1s ocurre a una sola energía en ausencia de un campo magnético, pero puede ocurrir a tres energías diferentes en presencia de un campo magnético.

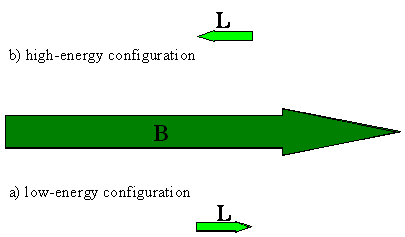
El\(m_l = 0\) estado, para el cual la componente del momento angular y de ahí también el momento magnético en la dirección del campo externo es cero, no experimenta interacción con el campo magnético. El\(m_l = +1\) estado, para el cual el momento angular en la dirección z es +y el momento magnético está en la dirección opuesta, contra el campo, experimenta una elevación de energía en presencia de un campo. Mantener el dipolo magnético contra la dirección del campo externo es como sostener una barra magnética pequeña con sus polos alineados exactamente opuestos a los polos de un imán grande (Figura\(\PageIndex{5}\)). Es una situación de mayor energía que cuando los momentos magnéticos están alineados entre sí.

Figura\(\PageIndex{4}\): Efecto de un campo magnético externo (\(B\)) sobre la energía de un dipolo magnético (\(L\)) orientado a) con y b) contra el campo magnético aplicado.

Ejercicio\(\PageIndex{4}\)

Llevar a cabo los pasos que van de Ecuación\(\ref{8.4.10}\) a Ecuación\(\ref{8.4.13}\).

Ejercicio\(\PageIndex{5}\)

Considera el efecto de cambiar el campo magnético sobre la magnitud de la división de Zeeman. Esboce un diagrama donde la intensidad del campo magnético está en el eje x y la energía de los tres orbitales 2p está en el eje y para mostrar la tendencia en la división de magnitudes con el aumento del campo magnético. Sea cuantitativo, calcule y grafique los valores numéricos exactos utilizando un paquete de software de su elección.

Ejercicio\(\PageIndex{6}\)

Con base en sus cálculos en Exercise\(\PageIndex{2}\) bosquejar un espectro de luminiscencia para el átomo de hidrógeno en el nivel n = 2 en un campo magnético de 1 Tesla. Proporcionar el valor numérico para cada una de las energías de transición. Use cm ^-1 o electrón voltios para las unidades de energía.