8.4: Un electrón tiene un momento angular de giro intrínseco
- Page ID
- 79633
- Entender el número cuántico de los electrones - spin.
- Entender cómo el espín está conectado a las propiedades magnéticas de los electrones y átomos.
- Entender cómo romper la degeneración a través de campos magnéticos aplicados externamente en electrones y átomos.
Imagínese hacer un experimento hipotético que conduciría al descubrimiento del espín electrónico. Su laboratorio acaba de adquirir un espectrómetro de microondas con capacidad de campo magnético variable. Probamos el nuevo instrumento con átomos de hidrógeno utilizando un campo magnético de 10 4 Gauss y buscamos la absorción de la radiación de microondas a medida que escaneamos la frecuencia de nuestro generador de microondas (Figura 8.4.1 ).
Finalmente vemos absorción a una frecuencia de fotones de microondas de\(28 \times 10^9\, Hz\) (28 gigahercios). Este resultado es realmente sorprendente desde varias perspectivas. Cada átomo de hidrógeno se encuentra en su estado fundamental, con el electrón en un orbital de 1s. La transición electrónica de energía más baja que predecimos con base en la teoría existente (la transición electrónica del estado fundamental (\(\psi _{100}\)a\(\psi _{21m}\)) requiere una energía que se encuentra en el ultravioleta de vacío (la línea inferior de Lyman a 121 nm), no en el microondas, región del espectro. Además, cuando variamos el campo magnético observamos que la frecuencia a la que se produce la absorción varía en proporción al campo magnético.
El efecto Zeeman: Rompiendo las degeneraciones con campos magnéticos
El magnetismo es el resultado del movimiento circular de las partículas cargadas. Esta propiedad se demuestra a escala macroscópica haciendo un electroimán a partir de una bobina de alambre y una batería. Los electrones que se mueven a través de la bobina producen un campo magnético, que se puede considerar que se origina en un dipolo magnético o un imán de barra. Los electrones en los átomos también están moviendo cargas con momento angular por lo que ellos también producen un dipolo magnético, razón por la cual algunos materiales son magnéticos. Un dipolo magnético interactúa con un campo magnético, y la energía de esta interacción viene dada por el producto escalar del momento dipolo magnético, y el campo magnético,\(\vec{B}\).
\[E_B = -\vec{\mu}_m \cdot \vec{B} \label {8.4.0} \]
Pieter Zeeman fue uno de los primeros en observar las divisiones de líneas espectrales en un campo magnético causado por esta interacción. En consecuencia, tales divisiones se conocen como el efecto Zeeman. (Figura 8.4.2 ). El valor de expectativa calculado para la energía total en este caso es la suma de la energía en ausencia del campo\(E_n\), más la energía Zeeman:
\[\begin{align} \left \langle E \right \rangle &= E_n + \dfrac {e \hbar B_z m_l}{2m_e} \\[4pt] &= E_n + \mu _B B_z m_l \label {8.4.13} \end{align} \]
El factor
\[ \dfrac {e \hbar}{2m_e} = - \gamma _e \hbar = \mu _B \label {8.4.14} \]
define la constante\(\mu _B\), llamada magnetón Bohr, que se toma como el momento magnético fundamental. Cuenta con unidades de\(9.2732 \times 10^{-21}\) ERG-Gauss o\(9.2732 \times 10^{-24}\) Joule/Tesla. Este factor te ayudará a relacionar los campos magnéticos, medidos en Gauss o Tesla, con energías, medidas en ergs o julios, para cualquier partícula con una carga y masa igual que un electrón.
La ecuación\ ref {8.4.13} demuestra que esa degeneración numérica\(m_l\) cuántica del átomo de hidrógeno es eliminada por el campo magnético aplicado externamente. Por ejemplo, los tres autoestados de átomos de hidrógeno\(|\psi _{211} \rangle\),\(|\psi _{21-1} \rangle\), y\(|\psi _{210} \rangle \) están degenerados en campo magnético cero, pero tienen diferentes energías en un campo magnético aplicado externamente (Figura 8.4.2 ).
El\(m_l = 0\) estado, para el cual la componente del momento angular y de ahí también el momento magnético en la dirección del campo externo es cero, no experimenta interacción con el campo magnético. El\(m_l = +1\) estado, para el cual el momento angular en la dirección z es +y el momento magnético está en la dirección opuesta, contra el campo, experimenta una elevación de energía en presencia de un campo. Mantener el dipolo magnético contra la dirección del campo externo es como sostener un imán de barra pequeña con sus polos alineados exactamente opuestos a los polos de un imán grande. Es una situación de mayor energía que cuando los momentos magnéticos están alineados entre sí.
Espín de electrones y el experimento Stern-Gerlach
Para descubrir cosas nuevas, los experimentalistas a veces deben explorar nuevas áreas a pesar de predicciones teóricas contrarias. Nuestra teoría del átomo de hidrógeno en este punto no da ninguna razón para buscar absorción en la región de microondas del espectro. Al hacer el loco experimento esbozado anteriormente, descubrimos que cuando un electrón está en la\(|1s \rangle\) órbita del átomo de hidrógeno, hay dos estados diferentes que tienen la misma energía. Cuando se aplica un campo magnético, se elimina esta degeneración, y la radiación de microondas puede provocar transiciones entre los dos estados. En el resto de esta sección, vemos lo que se puede deducir de esta observación experimental. Este experimento en realidad podría realizarse con espectrómetros de resonancia de espín electrónico disponibles hoy en día (Figura 8.4.1 ). Para explicar nuestras observaciones, un nuevo modelo para el átomo de hidrógeno. Nuestro modelo original para el átomo de hidrógeno representó el movimiento del electrón y el protón en nuestro mundo tridimensional; el nuevo modelo necesita algo más que pueda dar lugar a un efecto adicional parecido a Zeemano. Necesitamos una partícula cargada con momento angular para producir un momento magnético, igual que el obtenido por el movimiento orbital del electrón. Podemos postular que nuestra observación resulta de un movimiento del electrón que no fue considerado en la última sección - espín electrónico. Tenemos una partícula cargada girando sobre su eje. Luego tenemos carga moviéndose en círculo, momento angular, y un momento magnético, que interactúa con el campo magnético y nos da el efecto zeemano que observamos (Figura 8.4.2 ).
En 1920, Otto Stern y Walter Gerlach diseñaron un experimento, que sin querer llevó al descubrimiento de que los electrones tienen su propio giro individual, continuo incluso cuando se mueven a lo largo de su órbita de un átomo. Hoy en día, este espín electrónico está indicado por el cuarto número cuántico, también conocido como el Número Cuántico de Espín Electrónico y denotado por\(m_s\). En 1925, Samuel Goudsmit y George Uhlenbeck hicieron la afirmación de que las características del espectro de hidrógeno que no fueron examinadas podrían explicarse asumiendo que los electrones actúan como si tuviera un giro, que puede ser denotado por una flecha apuntando hacia arriba, que es +1/2, o una flecha apuntando hacia abajo, que es -1/2. El experimento de Stern y Gerlach que lo demostró se realizó con un haz de átomos de plata vaporizados que se dividieron en dos haces después de pasar por un campo magnético (Figura 8.4.2 ). Una explicación de esto es que un electrón tiene un campo magnético debido a su giro. Cuando se juntan electrones que tienen giros opuestos, no hay campo magnético neto porque los giros positivos y negativos se cancelan entre sí. El átomo de plata utilizado en el experimento tiene un total de 47 electrones, 23 de un tipo de espín y 24 de lo contrario. Debido a que los electrones del mismo giro se cancelan entre sí, el electrón desapareado en el átomo determinará el espín.
Spin Eigenstates y Eigenvalues
Para describir el espín electrónico desde una perspectiva mecánica cuántica, debemos tener funciones de onda de espín y operadores de espín. Las propiedades de los estados de espín se deducen de observaciones experimentales y por analogía con nuestro tratamiento de los estados que surgen del momento angular orbital del electrón. La característica importante del electrón giratorio es el vector de momento angular de espín, que etiquetamos\(S\) por analogía con el momento angular orbital\(L\). Definimos operadores de momento angular de giro con las mismas propiedades que encontramos para los operadores de momento angular rotacional y orbital. Después de todo, el momento angular es momento angular, sin importar si es de naturaleza orbital o de giro.
Encontramos que
\[ \hat {L}^2 | Y^{m_l} _l \rangle = l(l + 1) \hbar^2 | Y^{m_l}_l \rangle \label {8.4.1} \]
así que por analogía para los estados de giro, debemos tener
\[ \hat {S}^2 | \sigma ^{m_s} _s \rangle = s( s + 1) \hbar ^2 | \sigma ^{m_s}_s \rangle \label {8.4.2} \]
donde\(\sigma\) es una función de onda de espín con números cuánticos\(s\) y\(m_s\) que obedecen las mismas reglas que los números cuánticos\(l\) y\(m_l\) asociadas con la función de onda armónica esférica\(Y\). También encontramos que el proyecto del momento angular orbital en el eje z es
\[ \hat {L}_z | Y^{m_l}_l \rangle = m_l \hbar | Y^{m_l}_l \rangle \label {8.4.3} \]
así que por analogía, debemos tener una proyección similar para el momento angular de giro:
\[ \hat {S}_z | \sigma ^{m_s}_s \rangle = m_s \hbar | \sigma ^{m_s}_s \rangle \label {8.4.4} \]
Dado que\(m_l\) varía en pasos enteros de\(-l\) a\(+l\), también por analogía\(m_s\) varía en pasos enteros de\(-s\) a\(+s\). En nuestro experimento hipotético, observamos una transición de absorción, lo que significa que hay dos estados de espín. En consecuencia, los dos valores de\(m_s\) deben ser\(+s\) y\(-s\), y la diferencia en\(m_s\) para los dos estados, etiquetados f e i a continuación, debe ser el paso entero más pequeño, es decir, 1. El resultado de esta lógica es que
\[\begin{align} m_{s,f} - m_{s,i} &= 1 \nonumber\\[4pt] (+s) - (-s) &= 1 \nonumber\\[4pt] 2s &= 1 \nonumber\\[4pt] s &= \dfrac {1}{2} \label {8.4.5} \end{align} \]
Por lo tanto, nuestra conclusión es que la magnitud del número cuántico de espín es 1/2 y los valores para\(m_s\) son +1/2 y -1/2. Los dos estados de giro corresponden a girar en sentido horario y antihorario con proyecciones positivas y negativas del momento angular de giro sobre el eje z (Figura 8.4.3 ). Se llama al estado con proyección positiva,\(m_s\) = +1/2\(\alpha\); al otro se le llama\(\beta\). Estos estados de espín se etiquetan arbitrariamente\(\alpha\) y\(\beta\), y las funciones de onda de espín asociadas también son designadas por\(|\alpha \rangle \) y\(| \beta \rangle\).
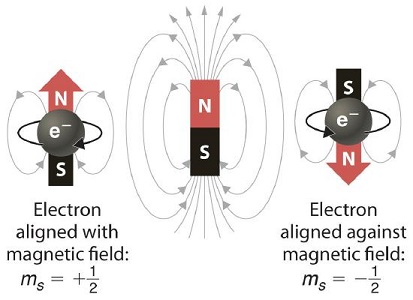
De la ecuación\(\ref{8.4.4}\), la magnitud del componente z del momento angular de giro,\(S_z\), viene dada por
\[S_z = m_s \hbar \label {8.4.6} \]
por lo que el valor de\(S_z\) es\(+ħ/2\) para el estado de giro\(\alpha\) y\(-ħ/2\) para el estado de giro\(\beta\). De ahí que concluimos que el estado de\(\alpha\) giro, donde el momento magnético se alinea contra la dirección del campo externo, tiene una energía mayor que el estado de\(\beta\) giro.
La superficie hipotética de Electron tendría que moverse más rápido que la velocidad de la luz para que gire lo suficientemente rápido como para producir el momento angular observado. Por lo tanto, un electrón no es simplemente una bola giratoria o un anillo y el espín electrónico parece ser un momento angular intrínseco de la partícula más que una consecuencia de la rotación de una partícula de carga como sugiere la Figura 8.4.3 . A pesar de ello, el término “espín electrónico” persiste en la lengua vernácula cuántica.
A pesar de que no conocemos sus formas funcionales, las funciones de onda de espín se toman para ser normalizadas y ortogonales entre sí.
\[ \int \alpha ^* \alpha \,d \tau _s = \int \beta ^* \beta \,d \tau _s = 1 \label {8.4.7a} \]
o en notación de braket
\[ \langle \alpha | \alpha \rangle = \langle \beta | \beta \rangle =1 \label{8.4.7b} \]
y
\[ \int \alpha ^* \beta\, d \tau _s = \int \beta ^* \alpha\, d \tau _s = 0 \label {8.4.8a} \]
o en notación de braket
\[ \langle \alpha | \beta \rangle = \langle \alpha | \beta \rangle = 0 \label{8.4.8b} \]
donde la integral está sobre la variable de giro\(\tau _s\).
Ahora vamos a aplicar estas deducciones a las observaciones experimentales en nuestro hipotético experimento de microondas en la Figura 8.4.1 . Podemos explicar la frecuencia de la transición (\(\nu\)= 28 gigahercios) que se observó en este hipotético experimento en términos del momento magnético del electrón giratorio y la fuerza del campo magnético. La energía fotónica\(h \nu\),, viene dada por la diferencia entre las energías de los dos estados,\(E_{\alpha}\) y\(E_{\beta}\)
\[\begin{align} \Delta E &= h \nu \\[4pt] &= E_{\alpha} - E_{\beta} \label {8-49}\end{align} \]
Las energías de estos dos estados consisten en la suma de la energía de un electrón en un orbital 1s,\(E_{1s}\), y la energía debida a la interacción del momento dipolo magnético de espín del electrón,\(\mu _s\), con el campo magnético,\(B\).
Los dos estados con valores distintos para el momento magnético de espín\(\mu _s\) se denotan por los subíndices\(\alpha\) y\(\beta\) (la versión de espín de la Ecuación\ ref {8.4.0}.
\[ \begin{align} E_{\alpha} &= E_{1s} - \mu _{s,\alpha} \cdot B \label {8-50} \\[4pt] E_{\beta} &= E_{1s} - \mu _{s,\beta} \cdot B \label {8-51} \end{align} \]
Sustituyendo las dos ecuaciones anteriores en la expresión para el fotón (Ecuación\ ref {8-49}) la energía da
\[\begin{align} h \nu &= E_{\alpha} - E_{\beta} \\[4pt] &= (E_{1s} - \mu _{s, \alpha} \cdot B) - (E_{1s} - \mu_{s,\beta} \cdot B) \label {8-52} \\[4pt] &= ( \mu _{s, \beta} - \mu _{s, \alpha}) \cdot B \label{8-53} \end{align} \]
Nuevamente por analogía con el momento angular orbital y el momento magnético discutidos anteriormente, tomamos el dipolo magnético de giro de cada estado de giro,\(\mu _{s, \alpha}\) y\(\mu _{s, \beta}\), para estar relacionado con el momento angular de giro total de cada estado,\(S_{\alpha}\) y\(S_{\beta}\), por una relación giromagnética de giro constante \(\gamma _s\), como se muestra a continuación.
\[ \mu _s = \gamma _s S \nonumber \]
o cada uno de los dos estados
\[\mu _{s, \alpha} = \gamma _s S_\alpha \nonumber \]
\[\mu _{s, \beta} = \gamma _s S_\beta \label {8-54} \]
Con la dirección del campo magnético definida como\(z\), el producto escalar en la Ecuación\ ref {8-53} se convierte en un producto de los componentes z del momento angular de giro,\(S_{z, \alpha}\) y\(S_{z, \beta}\), con el campo magnético externo.
Insertando los valores para\(S_{z,\alpha} = +\dfrac {1}{2} \hbar \) y\( S_{z, \alpha} = -\dfrac {1}{2} \hbar\) desde la ecuación\ ref {8.4.6} y reordenando la ecuación\ ref {8-53} rendimientos
\[ \dfrac {h \nu}{B} = - \gamma _s \hbar \label {8-56} \]
Calcular la relación\(\dfrac {h \nu}{B}\) a partir de nuestros resultados experimentales\(B = 10^4\, gauss\),\(\nu = 28 \times 10^9\, Hz\) cuando, nos da un valor para
\[- \gamma_s \hbar = 18.5464 \times 10^{-21}\, erg/gauss. \nonumber \]
Este valor es aproximadamente el doble del magnetón Bohr,\(-\gamma _e \hbar \), que se encuentra en la Ecuación\ ref {8.4.14} i.e.\(\gamma _s \hbar = 2.0023, \gamma _e \hbar\), o
\[\gamma _s = 2.0023 \gamma _e \label {8-57} \]
El factor de 2.0023 se llama factor g y explica la desviación de la relación giromagnética de espín del valor esperado para el movimiento orbital del electrón. En otras palabras, da cuenta de la transición de espín que se observa donde está en lugar de donde estaría si se mantiene la misma relación entre el momento magnético y el momento angular para los movimientos orbitales y de espín. El valor 2.0023 se aplica a un electrón que gira libremente; el acoplamiento del giro y el movimiento orbital de los electrones pueden producir otros valores para\(g\).
Llevar a cabo los cálculos que muestren que el factor g para espín electrónico es 2.0023.
Curiosamente, el concepto de espín electrónico y el valor g = 2.0023 siguen lógicamente de la teoría cuántica relativista de Dirac, que está más allá del alcance de esta discusión. Aquí se introdujo el espín electrónico como postulado para explicar observaciones experimentales. Los científicos suelen introducir dichos postulados paralelos al desarrollo de la teoría de la que se deduce naturalmente la propiedad.
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski


