1.9: Ecuaciones simultáneas no lineales

Consideramos dos Ecuaciones simultáneas de la forma

\[f(x, \ y) = 0, \label{1.9.1}\]

\[g(x, \ y) = 0 \label{1.9.2}\]

en el que las Ecuaciones no son lineales.

Como ejemplo, resolvamos las Ecuaciones

\[x^2 = \frac{a}{b-\cos y} \label{1.9.3}\]

\[x^3 - x^2 = \frac{a(y-\sin y \cos y)}{\sin^3 y} , \label{1.9.4}\]

en las que\(a\) y\(b\) son constantes cuyos valores se asumen dados en cualquier caso particular.

Esto puede parecer un par de Ecuaciones artificialmente ideadas, pero de hecho un par de Ecuaciones como esta sí aparecen en la teoría orbital.

Se sugieren aquí dos métodos para resolver las Ecuaciones.

En la primera, observamos que de hecho se\(x\) puede eliminar de las dos Ecuaciones para producir una sola Ecuación en\(y\):

\[F(y) = aR^3 - R^2 - 2SR - S^2 = 0, \label{1.9.5}\]

donde\[R = 1/(b-\cos y) \label{1.9.5a} \tag{1.9.5a}\]

y\[S = (y - \sin y \cos y ) / \sin^3 y . \label{1.9.5b} \tag{1.9.5b}\]

Esto se puede resolver mediante el método habitual de Newton-Raphson, que es la aplicación repetida de\(y = y − F / F^\prime\). El derivado de\(F\) con respecto a\(y\) es

\[F^\prime = 3aR^2 R^\prime - 2RR^\prime - 2(S^\prime R + SR^\prime) - 2SS^\prime \label{1.9.6}\]

donde\[R^\prime = -\frac{\sin y}{(b-\cos y)^2} \label{1.9.6a} \tag{1.9.6a}\]

y\[S^\prime = \frac{\sin y (1 - \cos 2y ) - 3\cos y (y- \frac{1}{2} \sin 2y)}{\sin^4 y} \label{1.9.6b} \tag{1.9.6b}\]

A pesar de lo que a primera vista puedan parecer algunas Ecuaciones bastante complicadas, se encontrará que el proceso de Newton-Raphson\(y = y − F / F^\prime\), es bastante sencillo de programar, aunque, con fines computacionales,\(F\) y\(F^\prime\) se escriben mejor como

\[F = -S^2 + R(-2S + R (-1 + aR)) , \label{1.9.7a} \tag{1.9.7a}\]

y

\[F^\prime = 3aR^2 R^\prime - 2(R+S)(R^\prime + S^\prime ) \label{1.9.7b} \tag{1.9.7b}\]

Veamos un ejemplo particular, digamos con\(a = 36\) y\(b = 4\). Por supuesto, debemos hacer una primera conjetura. En la aplicación orbital, descrita en el Capítulo 13, sugerimos una primera suposición. En el presente caso, con\(a = 36\) y\(b = 4\), una forma sería trazar gráficas de Ecuaciones\(\ref{1.9.3}\)\(\ref{1.9.4}\) y ver dónde se cruzan. Esto lo hemos hecho en la Figura 1.4, de la que vemos que y debe estar cerca de\(0.6\).

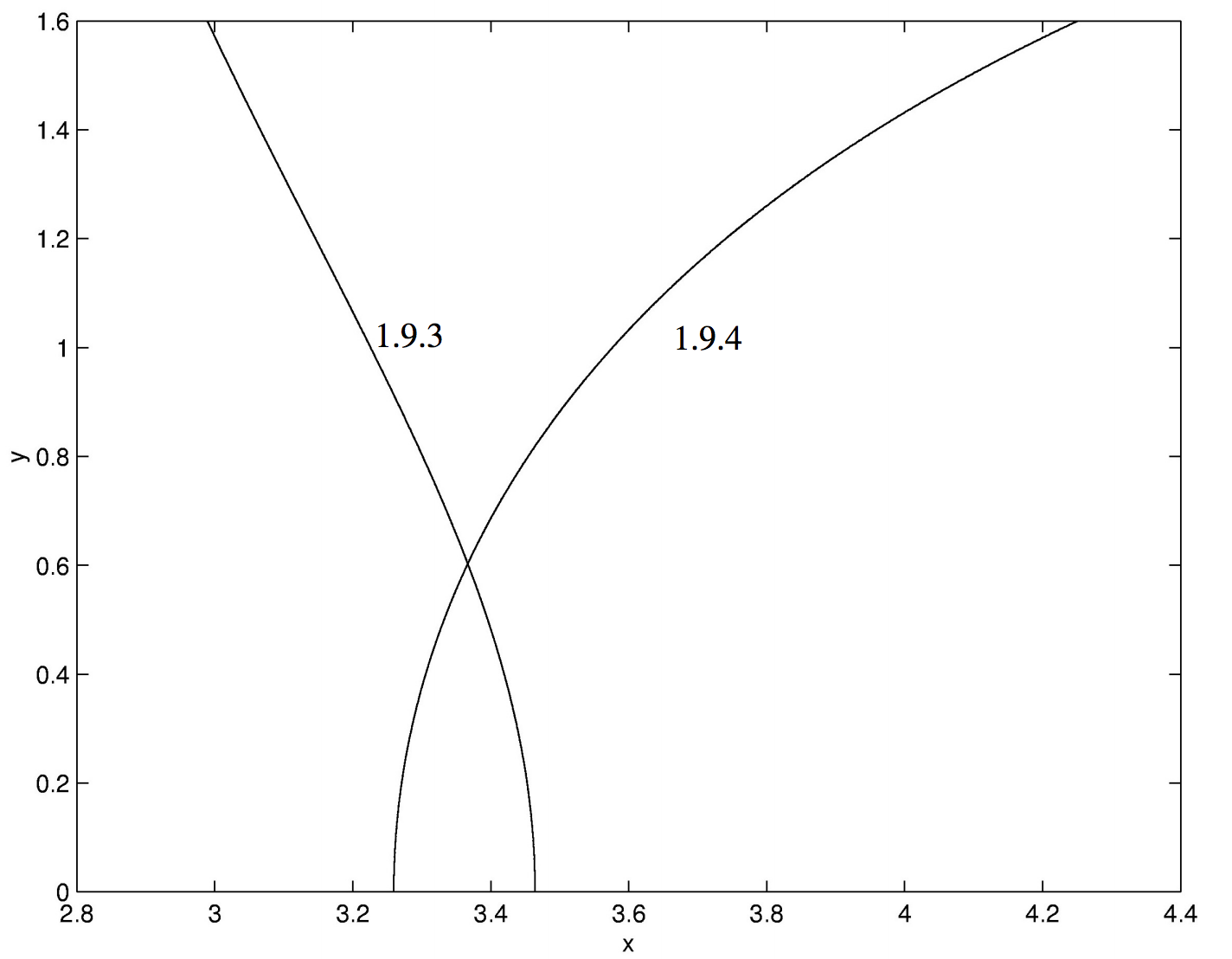
\(\text{FIGURE 1.4}\)
Ecuaciones\(\ref{1.9.3}\) y\(\ref{1.9.4}\) con\(a=36\) y\(b=4\).

Con una primera suposición de\(y = 0.6\), la convergencia a\(y = 0.60292\) se alcanza en dos iteraciones, y luego da cualquiera de las dos Ecuaciones originales\(x = 3.3666\).

Tuvimos suerte en este caso en que encontramos que pudimos eliminar una de las variables y así reducir el problema a una sola Ecuación sobre una desconocida. No obstante, habrá ocasiones en las que la eliminación de una de las incógnitas puede ser considerablemente más difícil o, en el caso de dos Ecuaciones trascendentales simultáneas, imposible por medios algebraicos. Casi siempre se puede utilizar el siguiente método iterativo, una extensión de la técnica Newton-Raphson. Lo describimos para dos Ecuaciones en dos incógnitas, pero se puede extender fácilmente a\(n\) Ecuaciones en\(n\) incógnitas.

Las Ecuaciones a resolver son

\[f(x, \ y) = 0 \label{1.9.8} \tag{1.9.8}\]

\[g(x, \ y) = 0 . \label{1.9.9} \tag{1.9.9}\]

Al igual que con la solución de una sola Ecuación, primero es necesario adivinar las soluciones. Esto podría hacerse en algunos casos por métodos gráficos. Sin embargo, muy a menudo, como es común con el método Newton-Raphson, la convergencia es rápida incluso cuando la primera conjetura es muy incorrecta.

Supongamos que las conjeturas iniciales\(y\) son\(x\),, dónde, son las soluciones correctas,\(h\) y\(k\) son los errores de nuestra suposición.\(x + h\)\(y + k\) Desde una expansión de Taylor de primer orden (o del sentido común, si se olvida la expansión Taylor),

\[f(x+h, y+k) \approx f(x,y) + hf_x + kf_y . \label{1.9.10} \tag{1.9.10}\]

Aquí\(f_x\) y\(f_y\) están las derivadas parciales y por supuesto\(f(x, \ y) = 0\). Las mismas consideraciones se aplican a la segunda Ecuación, por lo que llegamos a las dos Ecuaciones lineales en los errores\(h\),\(k\):

\[f_x h + f_y k = f , \label{1.9.11} \tag{1.9.11}\]

\[g_x h + g_y k = g. \label{1.9.12} \tag{1.9.12}\]

Estos se pueden resolver para\(h\) y\(k\):

\[h = \frac{g_y f - f_y g}{f_x g_y = f_y g_x}, \label{1.9.13} \tag{1.9.13}\]

\[k = \frac{f_x g - g_x f}{f_x g_y - f_y g_x}. \label{1.9.14} \tag{1.9.14}\]

Estos valores de\(h\) y luego\(k\) se restan de la primera conjetura para obtener una mejor conjetura. El proceso se repite hasta que los cambios en\(x\) y\(y\) son tan pequeños como se desee para la aplicación particular. Es fácil configurar un programa de computadora para resolver dos ecuaciones cualesquiera; todo lo que cambiará de un par de ecuaciones a otro son las definiciones de las funciones\(f\) y\(g\) y sus derivadas parciales.

En el caso de nuestro ejemplo, tenemos

\[f = x^2 - \frac{a}{b-\cos y} \label{1.9.15} \tag{1.9.15}\]

\[g = x^3 - x^2 - \frac{a(y-\sin y \cos y)}{\sin^3 y} \label{1.9.16} \tag{1.9.16}\]

\[f_x = 2x \tag{1.9.17} \label{1.9.17}\]

\[f_y = \frac{a\sin y}{(b- \cos y)^2} \label{1.9.18} \tag{1.9.18}\]

\[g_x = x(3x-2) \label{1.9.19} \tag{1.9.19}\]

\[g_y = \frac{a[3(y-\sin y \cos y) \cos y - 2\sin^3 y]}{\sin^4 y} \label{1.9.20} \tag{1.9.20}\]

En el caso particular donde\(a = 36\) y\(b = 4\), podemos comenzar con una primera conjetura (de la gráfica - Figura I.4) de\(y = 0.6\) y por lo tanto\(x = 3.3\). La convergencia a una parte en un millón se alcanza en tres iteraciones, siendo las soluciones\(x = 3.3666\),\(y = 0.60292\).

Una simple aplicación de estas consideraciones surge si se tiene que resolver una Ecuación polinómica\(f(z) = 0\), donde no hay raíces reales, y todas las soluciones para\(z\) son complejas. Entonces se limita a escribir\(z = x + iy\) y sustituir esto en la Ecuación polinómica. Luego equiparar las partes real e imaginaria por separado, para obtener dos Ecuaciones de la forma

\[R(x, \ y ) = 0 \label{1.9.21} \tag{1.9.21}\]

\[I(x, \ y ) = 0 \label{1.9.22} \tag{1.9.22}\]

y resolverlos para x e y. Por ejemplo, encontrar las raíces de la Ecuación

\[z^4 - 5z + 6 = 0 . \label{1.9.23} \tag{1.9.23}\]

Pronto se encontrará que tenemos que resolver

\[R(x, \ y) = x^4 - 6x^2 y^2 + y^4 - 5x + 6 = 0 \label{1.9.24} \tag{1.9.24}\]

\[I(x, \ y) = 4x^3 - 4xy^2 - 5 = 0 \label{1.9.25} \tag{1.9.25}\]

Se habrá observado que, para obtener la última Ecuación, hemos dividido por\(y\), lo cual es permisible, ya que sabemos\(z\) que es complejo. También notamos que\(y\) ahora solo ocurre como\(y^2\), así simplificará las cosas si lo dejamos\(y^2 = Y\), y luego resolveremos las Ecuaciones

\[f(x, Y) = x^4 - 6x^2 Y + Y^2 - 5x + 6 = 0 \label{1.9.26} \tag{1.9.26}\]

\[g(x,Y) = 4x^3 - 4xY - 5 = 0 \label{1.9.27} \tag{1.9.27}\]

Entonces es fácil resolver cualquiera de estos para\(Y\) como una función de\(x\) y por lo tanto graficar las dos funciones (figura\(\text{I.5}\)):

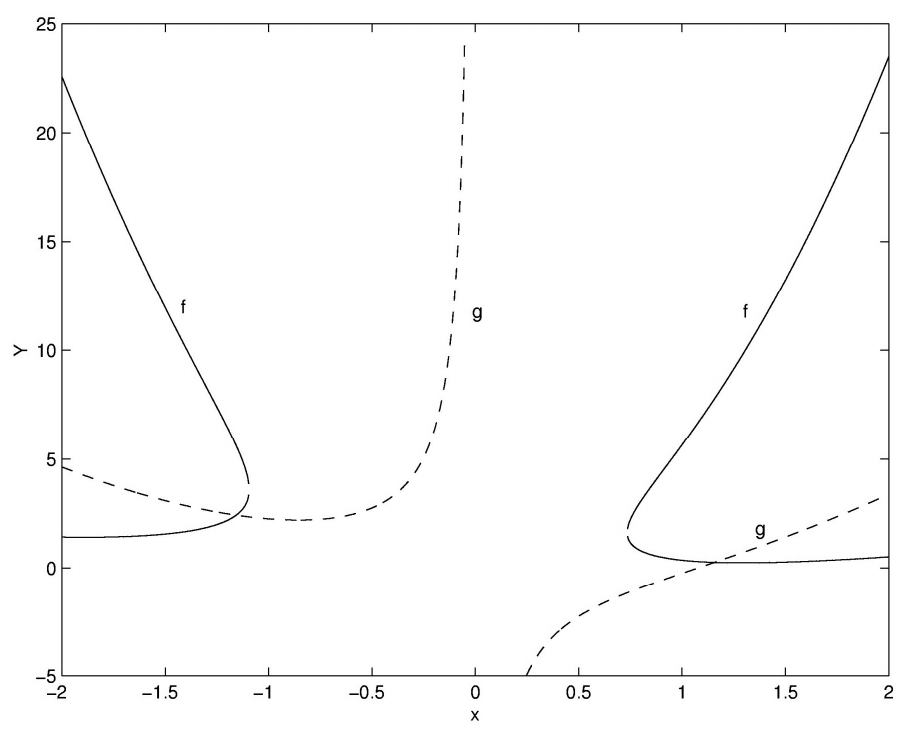
\(\text{FIGURE I.5}\)

Esto nos permite hacer una primera conjetura para las soluciones, a saber

\[x = -1.2, \quad Y = 2.4 \nonumber\]

y\[x= +1.2, \quad Y = 0.25818 \nonumber\]

Luego podemos refinar las soluciones mediante la técnica extendida de Newton-Raphson para obtener

\[x = -1.15697, \quad Y = 2.41899 \nonumber\]

\[x = +1.15697, \quad Y = 0.25818 \nonumber\]

así que las cuatro soluciones a la Ecuación original son

\[z = -1.15697 \pm 1.55531i \nonumber\]

\[z = 1.15697 \pm 0.50812i \nonumber\]