1.10:1.10-interpolación besseliana

En los días previos al uso generalizado de computadoras de alta velocidad, se hacía un uso extensivo de tablas impresas de las funciones matemáticas comunes. Por ejemplo, una tabla de la función Bessel\(J_0 (x)\) indicaría

\[J_0 (1.7) = 0.397 \ 984 \ 859 \nonumber\]

\[J_0(1.8) = 0.339 \ 986 \ 411 \nonumber\]

Si uno quisiera la función Bessel para\(x = 1.762\), uno tendría que interpolar entre los valores tabulados.

Hoy sería más fácil simplemente calcular la función Bessel para cualquier valor particular deseado del argumento\(x\), y hoy en día hay menos necesidad de tablas impresas o de saber interpolar. De hecho, la mayoría de los sistemas informáticos de hoy en día tienen rutinas internas que permitirán calcular las funciones más comunes como las funciones de Bessel incluso si uno solo tiene una noción nebulosa de lo que es una función de Bessel.

La necesidad no ha pasado del todo, sin embargo. Por ejemplo, en los cálculos orbitales, muchas veces necesitamos las coordenadas geocéntricas del Sol. Estos no son triviales para que el no especialista los calcule, y puede ser más fácil buscarlos en El Almanaque Astronómico, donde se tabula para todos los días del año, como, por ejemplo, el 14 de julio y el 15 de julio. Pero, si uno necesita\(y\) para el 14.395 de julio, ¿cómo se interpola?

En un mundo ideal, una función tabulada sería tabulada a intervalos suficientemente finos para que la interpolación lineal entre dos valores tabulados fuera adecuada para devolver la función al mismo número de cifras significativas que los puntos tabulados. El mundo no es perfecto, sin embargo, y para lograr tal perfección, el intervalo de tabulación tendría que cambiar a medida que la función cambiara más o menos rápidamente. Necesitamos saber, por tanto, cómo hacer interpolación no lineal.

Supongamos que una función\(y(x)\) está tabulada en\(x = x_1\) y\(x = x_2\),\(x_2 − x_1\) siendo el intervalo\(δx\). Si se desea encontrar el valor de\(y\) at\(x + \theta δx\), la interpolación lineal da

\[y(x_1 + \theta \Delta x) = y_1 + \theta (y_2 - y_1) = \theta y_2 + (1-\theta) y_1 , \label{1.10.1} \tag{1.10.1}\]

dónde\(y_1 = y(x_1)\) y\(y_2 = y(x_2)\). Aquí se supone que es una fracción entre\(0\) y\(1\); si\(\theta\) está fuera de este rango (eso es negativo, o mayor que\(1\)) estamos extrapolando, no interpolando, y eso siempre es algo peligroso de hacer.

Veamos ahora la situación en la que la interpolación lineal no es lo suficientemente buena. Supongamos que una función\(y(x)\) se tabula para cuatro puntos\(x_1, \ x_2, \ x_3, \ x_4\) del argumento\(x\), siendo los valores correspondientes de la función\(y_1, \ y_2, \ y_3, \ y_4\). Deseamos evaluar\(y\) para\(x = x_2 + \theta δx\), donde\(δx\) esta el intervalo\(x_2 - x_1\) o\(x_3 - x_2\) o\(x_4 - x_3\). La situación se ilustra en la figura\(\text{I.6A}\).

Un posible enfoque sería ajustar un polinomio a los cuatro puntos adyacentes:

\[y = a + bx + cx^2 + dx^3 . \]

Escribimos esta Ecuación para los cuatro puntos tabulados adyacentes y resolvemos para los coeficientes, y de ahí podemos evaluar la función para cualquier valor de\(x\) que nos guste en el intervalo entre\(x_1\) y\(x_4\). Desafortunadamente, esto bien podría implicar más esfuerzo computacional que evaluar la función original en sí.

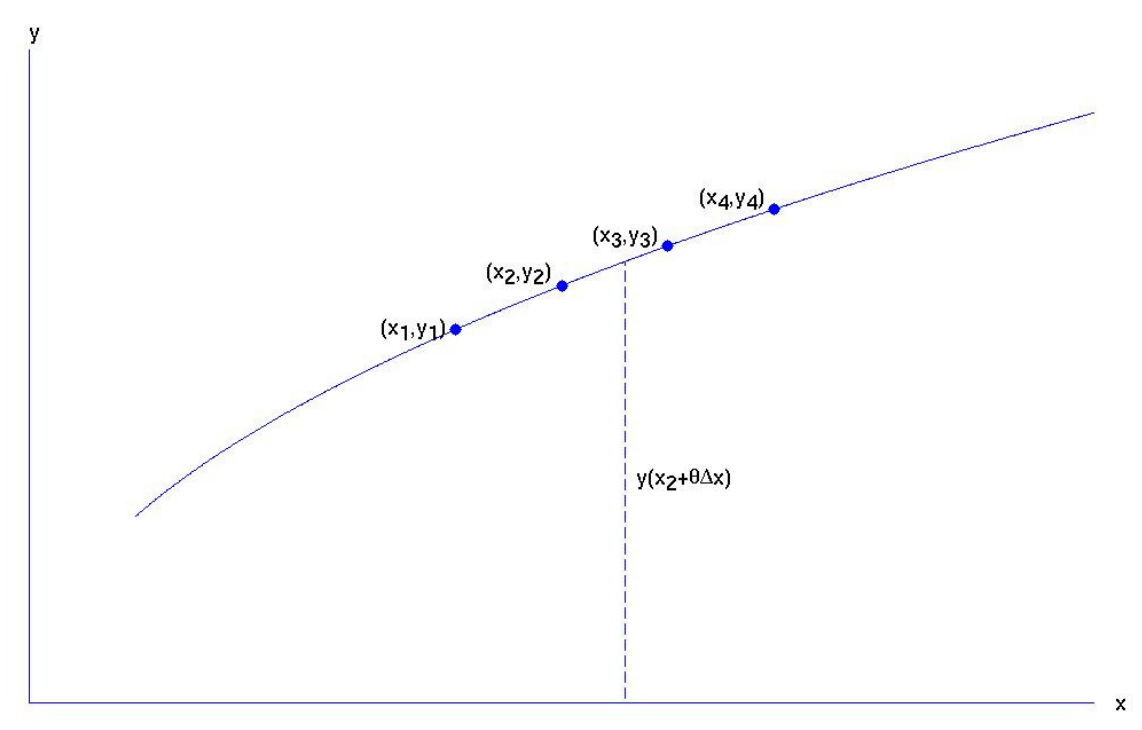
\(\text{FIGURE I.6A}\)

El problema se ha resuelto de manera conveniente en términos de cálculo de diferencias finitas, cuyo desarrollo lógico implicaría un capítulo sustancial adicional más allá del alcance pretendido de este libro. Por lo tanto solo proporciono el método solamente, sin pruebas.

La esencia del método es establecer una tabla de diferencias como se ilustra a continuación. Las dos primeras columnas son\(x\) y\(y\). Las entradas en las columnas restantes son las diferencias entre las dos entradas en la columna inmediatamente a la izquierda. Así, por ejemplo\(δ_{4.5} = y_5 - y_4\),\(δ_4^2 = δ_{4.5} - δ_{3.5}\),, etc.

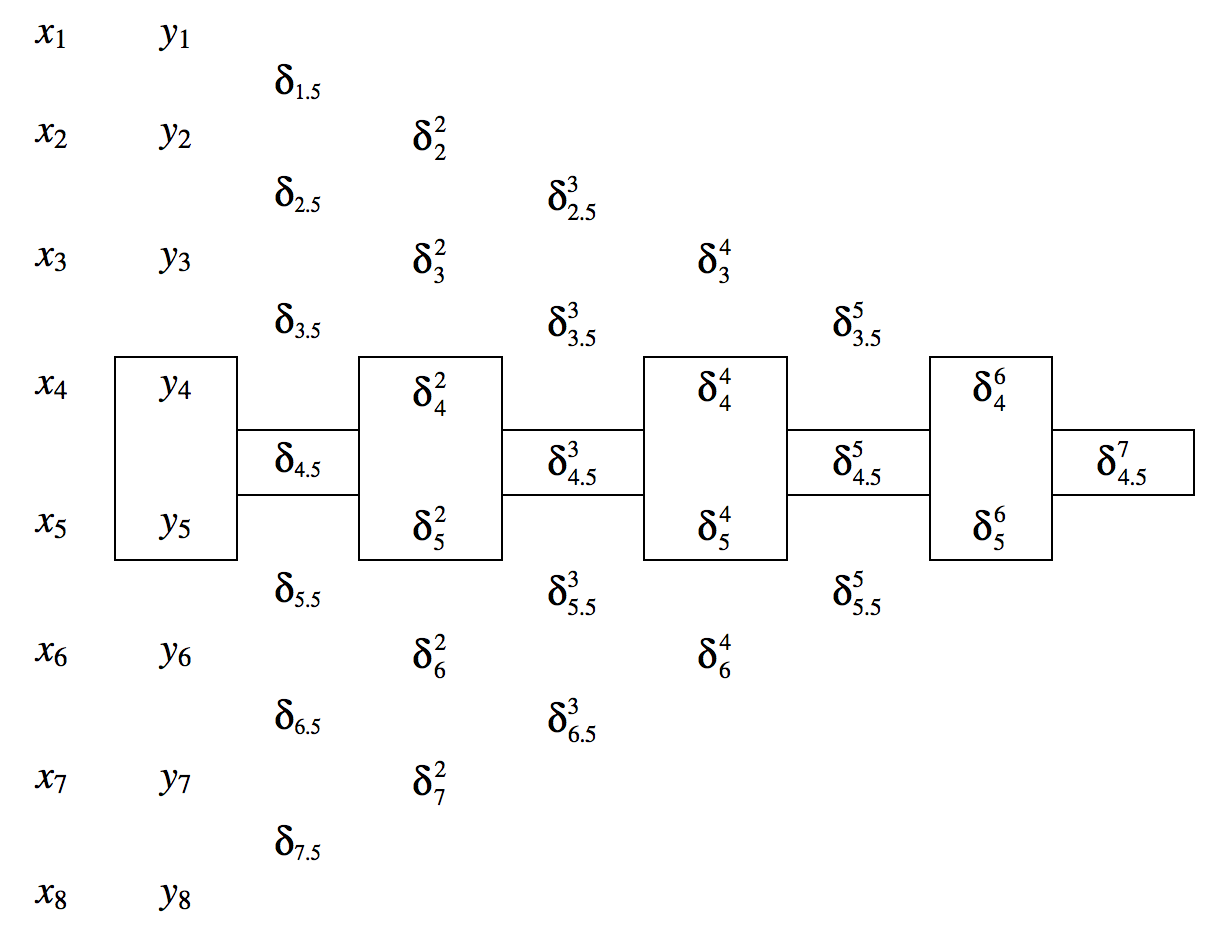
Supongamos que queremos encontrar\(y\) por un valor de\(x\) eso es una fracción\(\theta\) del camino de\(x_4\) a\(x_5\). La fórmula de interpolación de Bessel es entonces

\[y(x) = \frac{1}{2} (y_4 + y_5) + B_1 δ_{4.5} + B_2 ( δ_4^2 + δ_5^2) + B_3 δ_{4.5}^3 + B_4 (δ_4^4 + δ_5^4) + ... \label{1.10.3} \tag{1.10.3}\]

Aquí\(B_n\) están los coeficientes de interpolación besseliana, y los términos sucesivos entre paréntesis en la expansión son las sumas de los números en las casillas de la tabla.

Los coeficientes besselianos son

\[B_n (\theta) = \frac{1}{2} \begin{pmatrix} \theta + \frac{1}{2}n - 1 \\ n \end{pmatrix} \quad \text{if n is even,} \label{1.10.4} \tag{1.10.4}\]

y\[B_n (\theta) = \frac{\theta - \frac{1}{2}}{n} \begin{pmatrix} \theta + \frac{1}{2}n - \frac{3}{2} \\ n-1 \end{pmatrix} \quad \text{if n is odd.} \label{1.10.5} \tag{1.10.5}\]

La notación\(\begin{pmatrix} m \\ n \end{pmatrix}\) significa el coeficiente de x m en la expansión binomial de\((1 + x)^n\).

De manera explícita,

\[B_1 = \theta - \frac{1}{2} \label{1.10.6} \tag{1.10.6}\]

\[B_2 = \frac{1}{2} \theta ( \theta - 1 ) / 2! = \theta (\theta - 1) / 4 \label{1.10.7} \tag{1.10.7}\]

\[B_3 = (\theta - \frac{1}{2}) \theta ( \theta - 1) / 3! = \theta (0.5 + \theta (-1.5 + \theta ))/6 \label{1.10.8} \tag{1.10.8}\]

\[B_4 = \frac{1}{2} ( \theta + 1) \theta ( \theta - 1) ( \theta - 2) / 4 ! = \theta ( 2 + \theta ( -1 + \theta ( -2 + \theta ))) / 48 \label{1.10.0} \tag{1.10.9}\]

\[B_5 = (\theta - \frac{1}{2} ) ( \theta + 1) \theta ( \theta - 1) (\theta - 2) / 5 ! = \theta ( -1 + \theta ( 2.5 + \theta^2 (-2.5 + \theta )))/120 \label{1.10.10} \tag{1.10.10}\]

El lector debería convencerlo de que la fórmula de interpolación tomada hasta donde\(B_1\) es meramente interpolación lineal. La adición de términos sucesivamente más altos efectivamente ajusta una curva a más y más puntos alrededor del valor deseado y refleja cada vez más exactamente el cambio real de\(y\) con\(x\).

El cuadro anterior está tomado de El Almanaque Astronómico para 1997, y muestra la\(y\) coordenada del Sol durante ocho días consecutivos en julio. Las tres primeras columnas de diferencia están tabuladas, y es claro que otras columnas de diferencia son injustificadas.

Si queremos encontrar el valor de\(y\), por ejemplo, para el 4.746 de julio, tenemos\(\theta = 0.746\) y los tres primeros coeficientes de Bessel son

\ begin {array} {c c l}
B_1 & = & +0.246\\
B_2 & = & -0.047\ 371\\
B_3 & = & -0.007\ 768\ 844\
\ nonumber
\ end {array}

El lector puede verificar los siguientes cálculos para\(y\) a partir de la suma de los primeros 2, 3 y 4 términos de la fórmula de la serie de interpolación besseliana. La suma de los dos primeros términos es el resultado de la interpolación lineal.

Suma de los primeros 2 términos,\(y = 0.909 \ 580 \ 299\)
Suma de los primeros 3 términos,\(y = 0.909 \ 604 \ 723\)
Suma de los primeros 4 términos,\(y = 0.909 \ 604 \ 715\)

Siempre que la tabla no esté tabulada a intervalos inapropiadamente gruesos, rara vez es necesario pasar el tercer coeficiente de Bessel. En ese caso una fórmula de interpolación alternativa y equivalente (for\(t = t_4 + \theta \Delta t)\), que evita tener que construir una tabla de diferencias, es

\ begin {array} {c c l}
y (t_4 +\ theta\ Delta t) & = & -\ frac {1} {6}\ theta [(2 -\ theta (3-\ theta)) y_3 + (1 -\ theta) y_6]\\
& & +\ frac {1} {2} [(2 +\ theta (-1 +\ theta (-2 +\ theta))) y_4 +\ theta (2 +\ theta (1 -\ theta)) y_5].
\ end {matriz}

Los lectores deben comprobar que esto da la misma respuesta, al mismo tiempo que señalan que los paréntesis anidados hacen que el cálculo sea muy rápido y sean fáciles de programar ya sea en una calculadora o en una computadora.

Ejercicio\(\PageIndex{1}\): Bessel Coefficients

A partir de la siguiente tabla, construya una tabla de diferencias hasta la cuarta diferencia. Calcular los primeros cuatro coeficientes de Bessel para\(\theta = 0.73\). De ahí calcular el valor de\(y\) for\(x = 0.273\).

\ begin {array} {c c}
x & y\\
0.0 & + 0.381300\\
0.1 & + 0.285603\\
0.2 & + 0.190 092\\
0.3 & + 0.096327\\
0.4 & + 0.008 268\\
0.5 & - 0.067 725\\
\ end {array}

RESPUESTAS

• \(B_1 = +0.23\)
• \(B_2 - - 0.049275\)
• \(B_3 = -7.5555 \times 10^{-3}\)
• \(B_4 = +9.021841875 \times 10^{-3}\)
• \(y = 0.121289738\)

Nota: la tabla se calculó a partir de una fórmula, y la respuesta interpolada es correcta a nueve cifras significativas.

Ejercicio\(\PageIndex{2}\): Linear Interpolation vs. Besselian Interpolation

De la siguiente tabla de\(\sin x\), utilice la interpolación lineal y la interpolación besseliana para estimar\(\sin 51^\circ\) a tres cifras significativas.

\ begin {array} {c c}
x^\ circ &\ sin x\
\\
0 & 0.0\\
30 & 0.5\\
60 &\ sqrt {3} /2 - 0.86603\\
90 & 1.0\
\ end {array}

RESPUESTAS

• Por interpolación lineal,\(\sin 51^\circ = 0.634.\)
• Por interpolación besseliana,\(\sin 51^\circ = 0.776.\)

El valor correcto es 0.777. Debería quedar impresionado —pero hay más sobre interpolación por venir, en la Sección 1.11.