2.3: La Parábola

Definimos una parábola como el locus de un punto que se mueve de tal manera que su distancia desde una línea recta fija llamada directriz es igual a su distancia desde un punto fijo llamado focu s. a diferencia de la elipse, una parábola tiene solo un foco y una directriz. Sin embargo, la comparación de esta definición con la propiedad focus - directrix de la elipse (que también se puede usar para definir la elipse) muestra que la parábola puede ser considerada como una forma limitante de una elipse con excentricidad igual a la unidad.

Encontraremos la Ecuación a una parábola cuya directriz es la línea\(y = −q\) y cuyo foco es el punto\((q , 0)\). La figura\(\text{II.20}\) muestra la parábola. \(\text{F}\)es el foco y\(\text{O}\) es el origen del sistema de coordenadas. El vértice de la parábola está en el origen. En un contexto orbital, por ejemplo, la órbita de un cometa que se mueve alrededor del Sol en órbita parabólica, el Sol estaría en el foco\(\text{F}\), y la distancia entre vértice y foco sería la distancia perihelio, para lo cual el símbolo\(q\) se usa tradicionalmente en la teoría de la órbita.

\(\text{FIGURE II.20}\)

A partir de la figura\(\text{II.20}\), es evidente que la definición de la parábola\((\text{PF} = \text{PN})\) requiere que

\[(x-q)^2 + y^2 = (x+q)^2 , \label{2.4.1} \]

de la cual

\[y^2 = 4qx , \label{2.4.2}\]

que es la Ecuación a la parábola.

Ejercicio\(\PageIndex{1}\)

Esboce las siguientes parábolas:

1. \(y^2 = -4qx \)
2. \(x^2 = 4qy\)
3. \(x^2 = -4qy,\)
4. \((y-2)^2 = 4q (x-3).\)

La línea paralela al\(y\) eje -y que pasa por el foco es el recto latus. La sustitución de\(x = q\) en\(y^2 = 4ax\) muestra que el recto latus se cruza con la parábola en los dos puntos\((q , \pm 2q)\), y que la longitud\(l\) del recto semilatoso es\(2q\).

Las Ecuaciones

\[x = qt^2 , \quad y = 2qt \label{2.4.3} \]

son las Ecuaciones paramétricas a la parábola, para\(y^2 = 4qx\) los resultados de la eliminación de\(t\) entre ellas. Es decir, si\(t\) es alguna variable, entonces cualquier punto que satisfaga estas dos Ecuaciones se encuentra en la parábola.

La mayoría de los lectores sabrán que si una partícula se mueve con velocidad constante en una dirección y aceleración constante en ángulo recto a esa dirección, como con una bola proyectada en un campo gravitacional uniforme o un electrón que se mueve en un campo eléctrico uniforme, el camino es una parábola. En la dirección de velocidad constante la distancia es proporcional al tiempo, y en la dirección de aceleración constante, la distancia es proporcional al cuadrado del tiempo, y de ahí la trayectoria es una parábola.

Tangentes a una Parábola.

¿Dónde se\(y = mx + c\) cruza la línea recta con la parábola\(y^2 = 4qx\)? La respuesta se encuentra sustituyendo\(mx + c\) para\(y\) obtener, después del reordenamiento,

\[m^2 x^2 + 2(mc - 2q) x + c^2 = 0 . \label{2.4.4} \]

La línea es tangente si el discriminante es cero, lo que lleva a

\[c = q/m . \label{2.4.5} \]

Así una línea recta de la forma

\[y = mx + q/m \label{2.4.6} \]

es tangente a la parábola. La figura\(\text{II.22}\) ilustra esto para varias líneas, las pendientes de cada una\(5^\circ\) difieren por de la siguiente.

\(\text{FIGURE II.22}\)

Ahora derivaremos una Ecuación a la línea que es tangente a la parábola en el punto\((x_1 , y_1 )\).

\((x_1 , y_1) = (qt_1^2 , 2qt_1)\)Sea un punto sobre la parábola, y
Let\((x_2 , y_2) = (qt_2^2 , 2qt_2)\) sea otro punto sobre la parábola.

La línea que une estos dos puntos es

\[\frac{y-2qt_1}{x-qt_1^2} = \frac{2q(t_2 - t_1)}{q(t_2^2 - t_1^2)} = \frac{2}{t_2+t_1}. \label{2.4.7} \]

Ahora vamos a\(t_2\) acercarnos\(t_1\), coincidiendo finalmente con él. Poner\(t_1 = t_2 = t\) en la última ecuación resultados, después de la simplificación, en

\[ty = x + qt^2 , \label{2.4.8} \]

siendo la Ecuación a la tangente at\((qt^2 , 2qt )\).

Multiplicar por\(2q\):

\[2qty = 2q (x+qt^2) \label{2.4.9} \]

y se ve que la Ecuación a la tangente at\((x_1 , y_1 )\) es

\[y_1 y = 2q (x_1 + x). \label{2.4.10} \]

Hay una serie de interesantes propiedades geométricas, algunas de las cuales se dan aquí. Por ejemplo, si una tangente a la parábola en un punto\(P\) se encuentra con la directriz en\(Q\), entonces, al igual que para la elipse,\(P\) y\(Q\) subtiende un ángulo recto en el foco (figura\(\text{II.23}\)). La prueba es similar a la dada para la elipse, y se deja para el lector.

\(\text{FIGURE II.23}\)

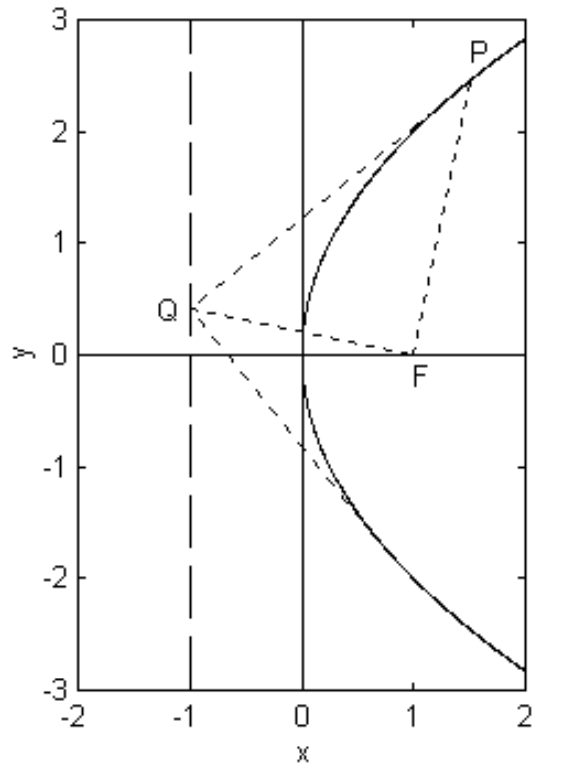
El lector recordará que las tangentes perpendiculares a una elipse se encuentran en el círculo director. El teorema análogo vis-à-vis la parábola es que las tangentes perpendiculares se encuentran en la directriz. Esto también se ilustra en la figura\(\text{II.23}\). El teorema no es especialmente importante en la teoría de órbita, y la prueba también se deja al lector.

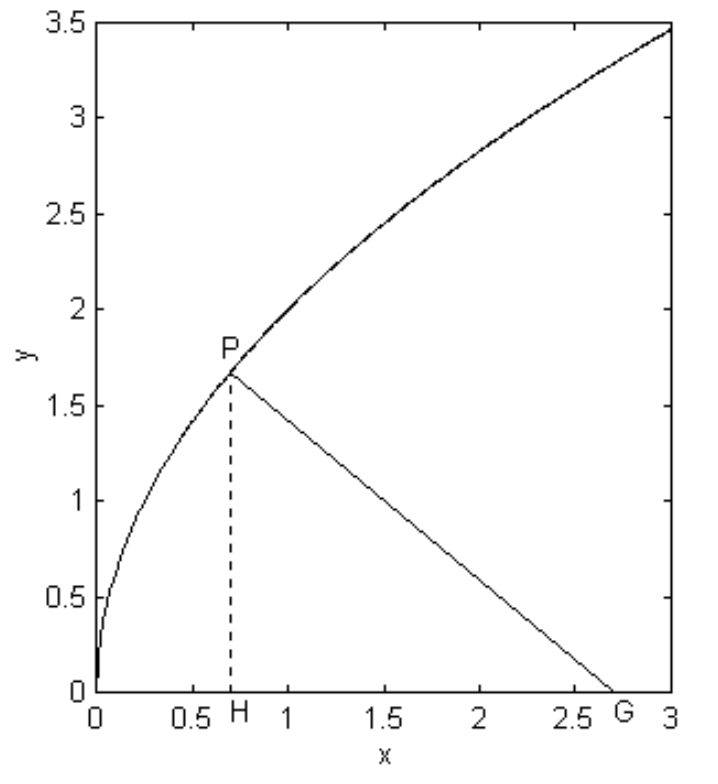
Dejar\(\text{PG}\) ser la normal a la parábola en el punto\(\text{P}\), encontrándose con el eje en\(\text{G}\) (figura\(\text{II.24}\)). Llamaremos a la longitud\(\text{GH}\) la subnormal. Una propiedad curiosa es que la longitud de\(\text{GH}\) es siempre igual a\(l\), la longitud del recto semi latus (que en la figura\(\text{II.24}\) es de longitud 2 − es decir, la ordenada donde\(x = 1\)), independientemente de la posición de\(\text{P}\). Esta prueba nuevamente se deja en manos del lector.

\(\text{FIGURE II.24}\)

Las siguientes dos propiedades geométricas, aunque no tienen aplicaciones inmediatas a la teoría de la órbita, ciertamente tienen aplicaciones a la astronomía.

\(\text{FIGURE II.25}\)

La tangente en\(\text{P}\) forma un ángulo\(\alpha\) con el\(x\) eje -y\(\text{PF}\) hace un ángulo\(\beta\) con el\(x\) eje -eje (figura\(\text{II.25}\)). Eso lo demostraremos\(\beta = 2\alpha\) y deduciremos una consecuencia interesante.

La Ecuación a la tangente (ver Ecuación\(\ref{2.4.8}\)) es\(ty = x + qt^2\), que muestra que

\[\tan \alpha = 1/t . \label{2.4.11} \]

Las coordenadas de\(\text{P}\) y\(\text{F}\) son, respectivamente,\(\left(qt^2 , 2qt \right)\) y\((q , 0)\), y así, desde el triángulo\(\text{PFH}\), nos encontramos.

\[\tan \beta = \frac{2t}{t^2-1}. \label{2.4.12}\]

Vamos\(\tau = 1/t\), entonces\(\tan \alpha = \tau\) y\(\tan \beta = 2\tau/(1 - \tau^2)\), lo que demuestra eso\(\beta = 2\alpha\).

Esto también muestra que el triángulo\(\text{JFP}\) es isósceles, con los ángulos en\(\text{J}\) y\(\text{P}\) cada ser\(\alpha\). Esto también se puede mostrar de la siguiente manera.

De la Ecuación\(ty = x + qt^2\), vemos que ese\(\text{J}\) es el punto\((−qt^2 , 0)\), así que eso\(\text{JF} = q (t^2 + 1)\).

Desde el triángulo\(\text{PFH}\), vemos que

\[(\text{PF})^2 = 4q^2 t^2 + q^2 \left(t^2 - 1 \right)^2 - q^2 \left( t^2 + 1 \right)^2 . \label{2.4.13}\]

Por lo tanto\[\text{PF} = \text{JF} . \label{2.4.14}\]

De cualquier manera, dado que el triángulo\(\text{JPF}\) es isósceles, se deduce eso\(\text{QP}\) y\(\text{PF}\) hacen el mismo ángulo\(\alpha\) a la tangente. Si la parábola es una sección transversal de un espejo telescópico, cualquier rayo de luz que llegue en paralelo al eje se enfocará\(\text{F}\), de manera que un espejo paraboloidal, usado en el eje, no sufra aberración esférica. (Esta propiedad se mantiene, por supuesto, solo para la luz paralela al eje del paraboloide, de modo que un espejo paraboloidal, sin algún tipo de corrección, da buenas imágenes sobre solo un campo de visión estrecho.)

Ahora considera lo que sucede cuando revuelves una taza de té. La superficie toma una forma que parece que podría parecerse a la parábola\(y = x^2 /(4q)\) - ver figura\(\text{II.26}\):

\(\text{FIGURE II.26}\)

Supongamos que el líquido está circulando a velocidad angular\(ω\). Una hoja de té flotando en la superficie se encuentra en equilibrio (en el marco de referencia giratorio) bajo tres fuerzas: su peso\(mg\), la fuerza centrífuga\(mω^2 x\) y la reacción normal\(R\). La normal a la superficie hace un ángulo\(\theta\) con la vertical (y la tangente hace un ángulo\(\theta\) con la horizontal) dado por

\[\tan \theta = \frac{ω^2x}{g}. \label{2.4.15} \]

Pero la pendiente de la parábola\(y = x^2 /(4q)\) es\(x/(2q)\), de manera que la superficie es efectivamente una parábola con recto semi latus\(2q = g/ω^2\).

Este fenómeno ha sido utilizado en Canadá para realizar un exitoso telescopio grande (diámetro\(6 \ \text{m}\)) en el que el espejo es un disco giratorio de mercurio que toma una forma perfectamente paraboloidal. Otro ejemplo es el método de fundición por rotación que se ha utilizado con éxito para la producción de grandes espejos telescópicos paraboloidales de vidrio sólido. En este proceso, el horno gira alrededor de un eje vertical mientras el vidrio fundido se enfría y finalmente se solidifica en el efecto paraboloidal requerido.

Ejercicio\(\PageIndex{1}\)

Los espejos de 6.5 metros de diámetro para los telescopios gemelos Magallanes en Las Campañas, Chile, tienen una relación focal\(f/1.25\). Fueron realizados por la técnica de spin casting en el Laboratorio Espejo de la Universidad de Arizona. ¿A qué velocidad habría tenido que girarse el horno para lograr la relación focal deseada? (Respuesta\(= 7.4 \ \text{rpm}\).) Observe que\(f/1.25\) es un paraboloide bastante profundo. Si este espejo hubiera sido hecho por molienda tradicional a partir de un disco sólido, ¿qué volumen de material habría tenido que eliminarse para hacer el paraboloide deseado? (Respuesta - ¡la friolera de 5.4 metros cúbicos, o unas 12 toneladas!)

Ecuación Polar a la Parábola

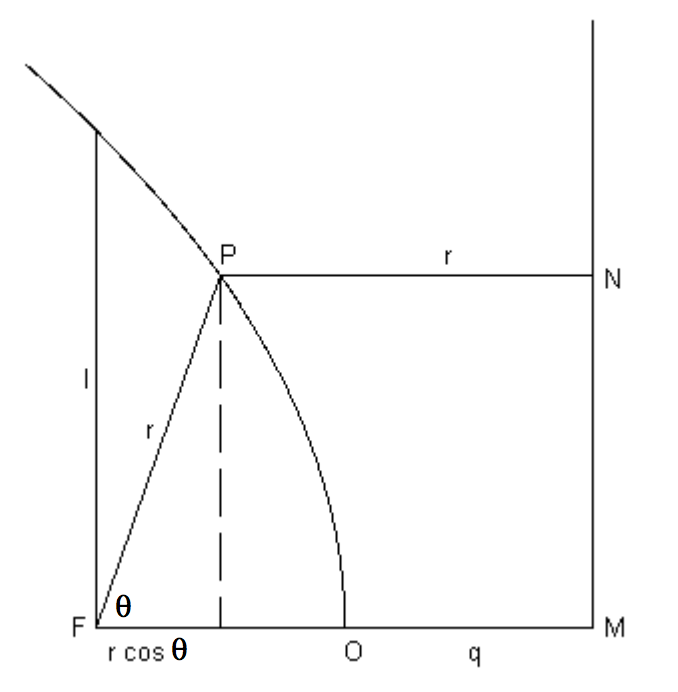
Al igual que con la elipse, elegimos el foco como polo y el eje de la parábola como línea inicial. Orientaremos la parábola para que el vértice esté hacia la derecha, como en la figura\(\text{II.27}\).

Recordamos la propiedad focus-directrix,\(\text{FP} = \text{PN}\). También, a partir de la definición de la directriz\(\text{FO}=\text{OM} = q\), de manera que\(\text{FM} = 2q = l\), la longitud del recto semi latus. Por lo tanto, es inmediatamente evidente a partir de la figura\(\text{II.27}\) que\(r \cos \theta + r = 2q = l\), de manera que la Ecuación polar a la parábola es

\[r = \frac{l}{1+ \cos \theta}. \label{2.4.16} \]

\(\text{FIGURE II.27}\)

Esto es lo mismo que la Ecuación polar a la elipse (Ecuación 2.3.36), con\(e = 1\) para la parábola. He dado diferentes derivaciones para la elipse y para la parábola; el lector podría querer intercambiar los dos enfoques y desarrollar la Ecuación 2.3.36 de la misma manera que hemos desarrollado la Ecuación\(\ref{2.4.16}\).

Cuando discutamos la hipérbola, les pediré que demuestren que su Ecuación polar también es la misma que 2.3.36. En otras palabras, la Ecuación 2.3.36 es la Ecuación a una sección cónica, y representa una elipse, parábola o hipérbola según si\(e<1, \ e=1 \ \text{or } e>1\).