11.3: Parábolas

Última actualización
Guardar como PDF

Page ID: 112769

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Gráfica de parábolas verticales
Gráfica parábolas horizontales
Resolver aplicaciones con parábolas

Esté preparado

Antes de comenzar, toma este cuestionario de preparación.

Gráfica:$y=-3 x^{2}+12 x-12$.
Si te perdiste este problema, revisa el Ejemplo 9.47.
Resuelve completando la plaza:$x^{2}-6 x+6=0$.
Si te perdiste este problema, revisa el Ejemplo 9.12.
Escribir en forma estándar:$y=3 x^{2}-6 x+5$.
Si te perdiste este problema, revisa el Ejemplo 9.59.

Parábolas Verticales de

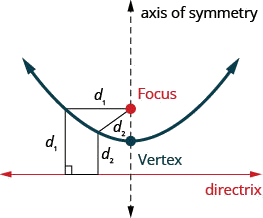
La siguiente sección cónica que veremos es una parábola. Definimos una parábola como todos los puntos en un plano que están a la misma distancia de un punto fijo y una línea fija. El punto fijo se llama foco, y la línea fija se llama directrix de la parábola.

Esta figura muestra un cono doble. La nappe inferior es intersecada por un plano de tal manera que la intersección forma una parábola. — Figura 11.2.1

Definición$\PageIndex{1}$: Parabola, Focus, and Directrix

Una parábola son todos los puntos en un plano que están a la misma distancia de un punto fijo y una línea fija. El punto fijo se llama foco, y la línea fija se llama directrix de la parábola.

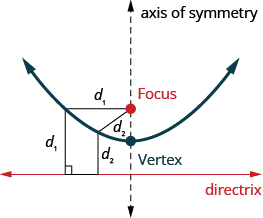
Esta figura muestra una parábola que se abre hacia arriba. Debajo de la parábola hay una línea horizontal etiquetada directrix. Una línea discontinua vertical a través del centro de la parábola se etiqueta como eje de simetría. El punto donde el eje intersecta la parábola se etiqueta como vértice. Un punto en el eje, dentro de la parábola se etiqueta foco. Una línea perpendicular a la directrix conecta la directrix a un punto en la parábola y otra línea conecta este punto con el foco. Ambas líneas son de la misma longitud. — Figura 11.2.2

Anteriormente, aprendimos a graficar las parábolas verticales a partir de la forma general o la forma estándar usando propiedades. Esos métodos también funcionarán aquí. Resumiremos las propiedades aquí.

Parabolas Verticales

Cuadro 11.2.1
	Forma general $y=a x^{2}+b x+c$	Forma estándar $y=a(x-h)^{2}+k$
Orientación	\ (y=a x^ {2} +b x+c\) ">$a>0$ arriba;$a<0$ abajo	\ (y=a (x-h) ^ {2} +k\) ">$a>0$ arriba;$a<0$ abajo
Eje de simetría	\ (y=a x^ {2} +b x+c\) ">$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k\) ">$x=h$
Vertex	\ (y=a x^ {2} +b x+c\) ">Sustituir$x=-\dfrac{b}{2 a}$ y resolver por$y .$	\ (y=a (x-h) ^ {2} +k\) ">$(h, k)$
$y$-interceptar	\ (y=a x^ {2} +b x+c\) ">Dejar$x=0$	\ (y=a (x-h) ^ {2} +k\) ">Dejar$x=0$
$x$-intercepta	\ (y=a x^ {2} +b x+c\) ">Dejar$y=0$	\ (y=a (x-h) ^ {2} +k\) ">Dejar$y=0$

Las gráficas muestran cómo se ven las parábolas cuando se abren hacia arriba o hacia abajo. Su posición en relación con el eje$x$ - o$y$ -eje no es más que un ejemplo.

Esta figura muestra dos parábolas con eje x es igual a h y vértice h, k. La de la izquierda se abre y A es mayor que 0. El de la derecha se abre hacia abajo. Aquí A es menor que 0. — Figura 11.2.3

Para graficar una parábola a partir de estas formas, se utilizaron los siguientes pasos.

Graficando Parábolas Verticales

Cómo Graficar Parabolas Verticales$y=a x^{2}+b x+c$ o$f(x)=a(x-h)^{2}+k$ usar Propiedades.

Paso 1: Determinar si la parábola se abre hacia arriba o hacia abajo.
Paso 2. Encuentra el eje de simetría.
Paso 3. Encuentra el vértice.
Paso 4. Encuentra la$y$ -intercepción. Encuentra el punto simétrico a la$y$ intersección a través del eje de simetría.
Paso 5. Encuentra las$x$ -intercepciones.
Paso 6. Grafica la parábola.

El siguiente ejemplo revisa el método de graficar una parábola a partir de la forma general de su ecuación.

Ejemplo$\PageIndex{1}$

$y=-x^{2}+6 x-8$Gráfica usando propiedades.

Solución:

Cuadro 11.2.2
	$ \begin{align} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt] \color{black}{y} &=-x^{2}+6 x-8 \end{align}$
Ya que$a$ es$-1$, la parábola se abre hacia abajo.
$.$
Para encontrar el eje de simetría, encontrar$x=-\dfrac{b}{2 a}$.	$ \begin{align} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align}$
	El eje de simetría es$x=3$.
	$.$
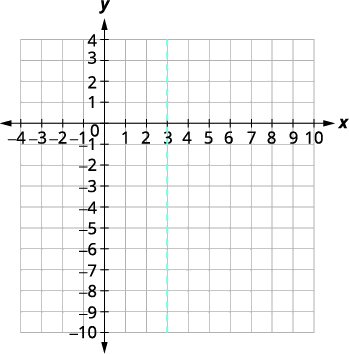El vértice está en la línea$x=3$.	$y=-x^{2}+6 x-8$
Vamos$x=3$.	$.$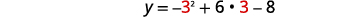
	$\begin{align} y &=-9+18-8 \\[4pt] y &=1 \end{align}$
	El vértice es$(3,1)$.
	$.$
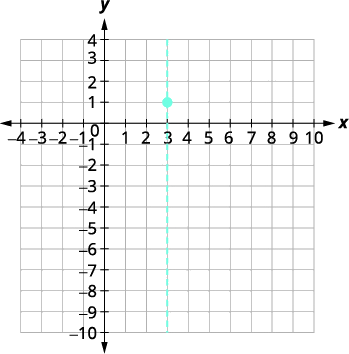La$y$ -intercepción ocurre cuando$x=0$.	$y=-x^{2}+6 x-8$
Sustituto$x=0$.	$y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8$
Simplificar.	$y=-8$
	El$y$ -intercepto es$(0,-8)$.
El punto$(0,−8)$ está a tres unidades a la izquierda de la línea de simetría. El punto tres unidades a la derecha de la línea de simetría es$(6,−8)$.	Punto simétrico a la$y$ -intercepción es$(6,−8)$.
	$.$
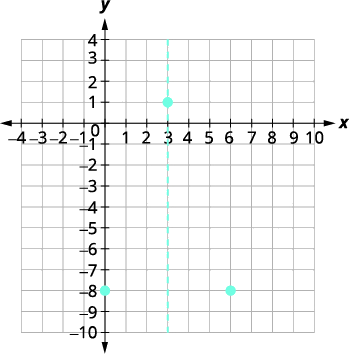La$x$ -intercepción ocurre cuando$y=0$.	$y=-x^{2}+6 x-8$
Vamos$y=0$.	$\color{red}{0} \color{black}{=}-x^{2}+6 x-8$
Factivar el GCF.	$0=-\left(x^{2}-6 x+8\right)$
Factorial el trinomio.	$0=-(x-4)(x-2)$
Resolver para$x$.	$x=4, \quad x=2$
	Los$x$ -interceptos son$(4,0),(2,0)$.
Grafica la parábola.	$.$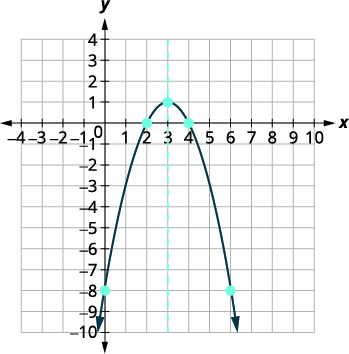

Ejercicio$\PageIndex{1}$

$y=-x^{2}+5 x-6$Gráfica usando propiedades.

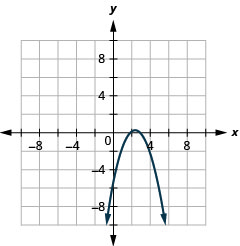
Contestar: $Esta gráfica muestra una parábola que se abre hacia abajo, con intercepciones x (2, 0) y (3, 0) e intercepción y (0, 6 negativo).$
Figura 11.2.24

Ejercicio$\PageIndex{2}$

$y=-x^{2}+8 x-12$Gráfica usando propiedades.

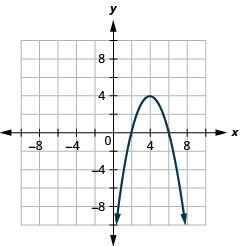
Contestar: $Esta gráfica muestra una parábola que se abre hacia abajo, con vértice (4, 4) e intercepciones x (2, 0) y (6, 0).$
Figura 11.2.25

El siguiente ejemplo revisa el método de graficar una parábola a partir de la forma estándar de su ecuación,$y=a(x-h)^{2}+k$.

Ejemplo$\PageIndex{2}$

Escribe$y=3 x^{2}-6 x+5$ en forma estándar y luego usa propiedades de forma estándar para graficar la ecuación.

Solución:

Cuadro 11.2.3
Reescribe la función en$y=a(x-h)^{2}+k$ forma completando el cuadrado.	$\begin{align} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3 \\[4pt] y &=3(x-1)^{2}+2 \end{align}$
Identificar las constantes$a, h, k$.	$a=3, h=1, k=2$
Ya que$a=2$, la parábola se abre hacia arriba.
$.$
El eje de simetría es$x=h$.	El eje de simetría es$x=1$.
El vértice es$(h,k)$.	El vértice es$(1,2)$.
Encuentra la$y$ -intercepción sustituyendo$x=0$,	$ \begin{align} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align} $
	$y$-interceptar$(0,5)$
Encuentra el punto simétrico a$(0,5)$ través del eje de simetría.	$(2,5)$
Encuentra las$x$ -intercepciones.	$\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}$
	La raíz cuadrada de un número negativo nos dice que las soluciones son números complejos. Entonces no hay$x$ -intercepciones.
Grafica la parábola.	$.$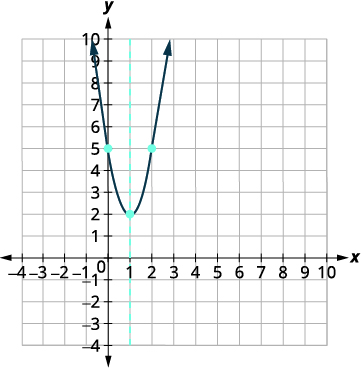

Ejercicio$\PageIndex{3}$

Escribir$y=2 x^{2}+4 x+5$ en forma estándar y
utilizar propiedades de forma estándar para graficar la ecuación.

Contestar

$y=2(x+1)^{2}+3$

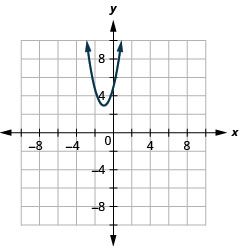
Esta gráfica muestra una parábola abriéndose hacia arriba, con vértice (negativo 1, 3) e intersección y (0, 5). Tiene el punto menos (2, 5) en él. — Figura 11.2.28

Ejercicio$\PageIndex{4}$

Escribir$y=-2 x^{2}+8 x-7$ en forma estándar y
utilizar propiedades de forma estándar para graficar la ecuación.

Contestar

$y=-2(x-2)^{2}+1$

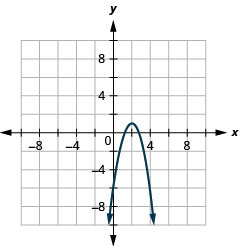
Esta gráfica muestra una parábola que se abre hacia abajo, con vértice (2, 1) y eje de simetría x es igual a 2. Su intercepción y es (0, negativo 7). — Figura 11.2.29

Gráfica Parábolas Horizontales

Nuestro trabajo hasta el momento sólo se ha ocupado de las parábolas que se abren hacia arriba o hacia abajo. Ahora vamos a mirar las parábolas horizontales. Estas parábolas se abren ya sea a la izquierda o a la derecha. Si cambiamos el$x$ y$y$ en nuestras ecuaciones anteriores por parábolas, obtenemos las ecuaciones para las parábolas que se abren a la izquierda o a la derecha.

Parabolas Horizontales

Cuadro 11.2.4
	Forma general $x=a y^{2}+b y+c$	Forma estándar $x=a(y-k)^{2}+h$
Orientación	\ (x=a y^ {2} +b y+c\) ">$a>0$ derecha;$a<0$ izquierda	\ (x=a (y-k) ^ {2} +h\) ">$a>0$ derecha;$a<0$ izquierda
Eje de simetría	\ (x=a y^ {2} +b y+c\) ">$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h\) ">$y=k$
Vertex	\ (x=a y^ {2} +b y+c\) ">Sustituir$y=-\dfrac{b}{2 a}$ y resolver por$x .$	\ (x=a (y-k) ^ {2} +h\) ">$(h, k)$
$x$-intercepta	\ (x=a y^ {2} +b y+c\) ">Dejar$x=0$	\ (x=a (y-k) ^ {2} +h\) ">Dejar$x=0$
$y$-interceptar	\ (x=a y^ {2} +b y+c\) ">Dejar$y=0$	\ (x=a (y-k) ^ {2} +h\) ">Dejar$y=0$

Las gráficas muestran cómo se ven las parábolas cuando están a la izquierda o a la derecha. Su posición en relación con el eje$x$ - o$y$ -eje no es más que un ejemplo.

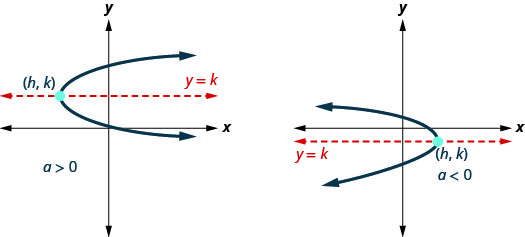
Esta figura muestra dos parábolas con eje de simetría y es igual a k,) y vértice (h, k La de la izquierda está etiquetada como mayor que 0 y se abre a la derecha. La otra parábola se abre a la izquierda. — Figura 11.2.30

Al mirar estas parábolas, ¿sus gráficas representan una función? Dado que ambas gráficas fallarían en la prueba de línea vertical, no representan una función.

Graficar una parábola que se abre a la izquierda o a la derecha es básicamente lo mismo que hicimos para las parábolas que se abren hacia arriba o hacia abajo, con la inversión de las$y$ variables$x$ y.

Cómo: Gráfica Parábolas Horizontales$y=a x^{2}+b x+c$ or $f(x)=a(x-h)^{2}+k$ using Properties

Paso 1: Determinar si la parábola se abre a la izquierda o a la derecha.
Paso 2: Encuentra el eje de simetría.
Paso 3: Encuentra el vértice.
Paso 4: Encuentra la$x$ -intercepción. Encuentra el punto simétrico a la$x$ intersección a través del eje de simetría.
Paso 5: Encuentra las$y$ -intercepciones.
Paso 6: Grafica la parábola.

Ejemplo$\PageIndex{3}$

$x=2 y^{2}$Gráfica usando propiedades.

Solución:

Cuadro 11.2.5
	$.$
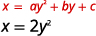Ya que$a=2$, la parábola se abre a la derecha.
$.$
Para encontrar el eje de simetría, encontrar$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{0}{2(2)}$
	$y=0$
	El eje de simetría es$y=0$.
El vértice está en la línea$y=0$.	$x=2 y^{2}$
Vamos$y=0$.	$.$
	$x=0$
	El vértice es$(0,0)$.

Dado que el vértice es$(0,0)$, tanto las intercepciones$x$ - como las$y$ -intercepciones son el punto$(0,0)$. Para graficar la parábola necesitamos más puntos. En este caso es más fácil elegir valores de$y$.

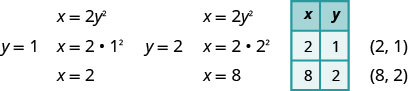
En la ecuación x es igual a 2 y al cuadrado, cuando y es 1, x es 2 y cuando y es 2, x es 8. Los puntos son (2, 1) y (8, 2). — Figura 11.2.38

También trazamos los puntos simétricos a$(2,1)$ y a$(8,2)$ través del$y$ eje -eje, los puntos$(2,−1),(8,−2)$.

Grafica la parábola.

Esta gráfica muestra la parábola de apertura derecha con vértice (0, 0). En él se marcan cuatro puntos: punto (2, 1), punto (2, negativo 1), punto (8, 2) y punto (8 menos 2). — Figura 11.2.39

Ejercicio$\PageIndex{5}$

$x=y^{2}$Gráfica usando propiedades.

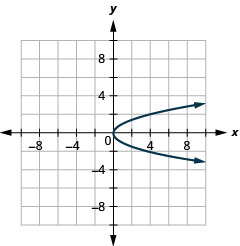
Contestar: $Esta gráfica muestra la parábola de apertura derecha con vértice en origen. Dos puntos en él son (4, 2) y (4, negativo 2).$
Figura 11.2.40

Ejercicio$\PageIndex{6}$

$x=-y^{2}$Gráfica usando propiedades.

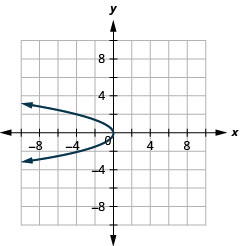
Contestar: $Esta gráfica muestra la parábola de apertura izquierda con vértice en origen. Dos puntos en él son (negativo 4, 2) y (negativo 4, negativo 2).$
Figura 11.2.41

En el siguiente ejemplo, el vértice no es el origen.

Ejemplo$\PageIndex{4}$

$x=-y^{2}+2 y+8$Gráfica usando propiedades.

Solución:

Cuadro 11.2.6
	$.$
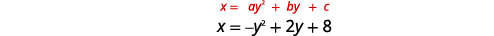Ya que$a=-1$, la parábola se abre a la izquierda.
$.$
Para encontrar el eje de simetría, encontrar$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{2}{2(-1)}$
	$y=1$
	El eje de simetría es$y=1$.
El vértice está en la línea$y=1$.	$x=-y^{2}+2 y+8$
Vamos$y=1$.	$.$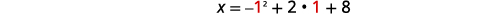
	$x=9$
	El vértice es$(9,1)$.
La$x$ -intercepción ocurre cuando$y=0$.	$x=-y^{2}+2 y+8$
	$.$
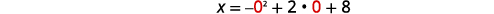	$x=8$
	El$x$ -intercepto es$(8,0)$.
El punto$(8,0)$ es una unidad por debajo de la línea de simetría. El punto simétrico una unidad por encima de la línea de simetría es$(8,2)$	El punto simétrico es$(8,2)$.
La$y$ -intercepción ocurre cuando$x=0$.	$x=-y^{2}+2 y+8$
Sustituto$x=0$.	$0=-y^{2}+2 y+8$
Resolver.	$y^{2}-2 y-8=0$
	$(y-4)(y+2)=0$
	$y=4, \quad y=-2$
	Los$y$ -interceptos son$(0,4)$ y$(0,-2)$.
Conecta los puntos para graficar la parábola.	$.$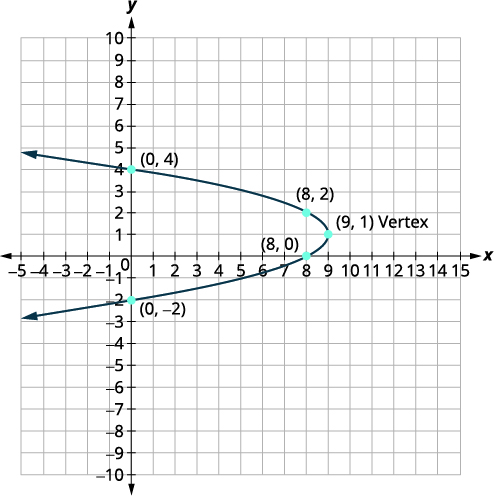

Ejercicio$\PageIndex{7}$

$x=-y^{2}-4 y+12$Gráfica usando propiedades.

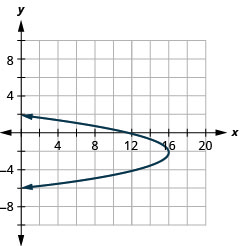
Contestar: $Esta gráfica muestra la parábola de apertura izquierda con vértice (16, negativo 2) e intersección x (12, 0).$
Figura 11.2.58

Ejercicio$\PageIndex{8}$

$x=-y^{2}+2 y-3$Gráfica usando propiedades.

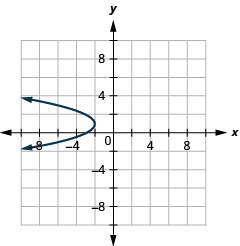
Contestar: $Esta gráfica muestra la parábola de apertura izquierda con vértice (negativo 2, 1) y x interceptar menos (3, 0).$
Figura 11.2.59

En el Cuadro 11.2.4, vemos la relación entre la ecuación en forma estándar y las propiedades de la parábola. El cuadro Cómo hacer enumera los pasos para graficar una parábola en la forma estándar$x=a(y-k)^{2}+h$. Utilizaremos este procedimiento en el siguiente ejemplo.

Ejemplo$\PageIndex{5}$

Gráfica$x=2(y-2)^{2}+1$ usando propiedades.

Solución:

Cuadro 11.2.7
	$.$
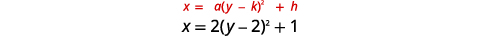Identificar las constantes$a, h, k$.	$a=2, h=1, k=2$
Ya que$a=2$, la parábola se abre a la derecha.
$.$
El eje de simetría es$y=k$.	El eje de simetría es$y=2$.
El vértice es$(h,k)$.	El vértice es$(1,2)$.
Encuentra la$x$ -intercepción sustituyendo$y=0$.	$x=2(y-2)^{2}+1$ $x=2(0-2)^{2}+1$ $x=9$
	El$x$ -intercepto es$(9,0)$.
Encuentra el punto simétrico a$(9,0)$ través del eje de simetría.	$(9,4)$
Encuentra las$y$ -intercepciones. Vamos$x=0$.	$\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}$
	Un cuadrado no puede ser negativo, por lo que no hay una solución real. Entonces no hay$y$ -intercepciones.
Grafica la parábola.	$.$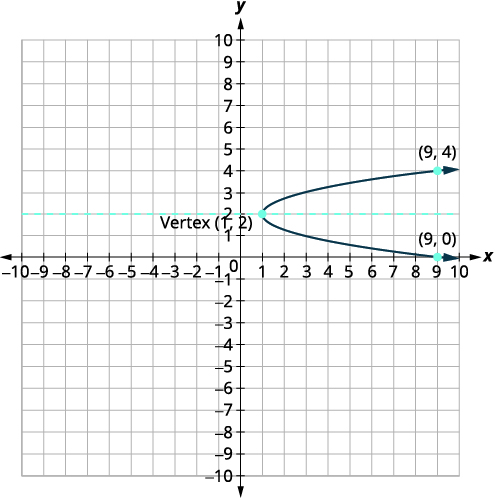

Ejercicio$\PageIndex{9}$

Gráfica$x=3(y-1)^{2}+2$ usando propiedades.

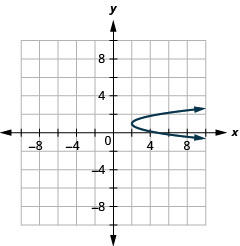
Contestar: $Esta gráfica muestra una parábola que se abre a la derecha con vértice (2, 1) y x intercepción (5, 0).$
Figura 11.2.63

Ejercicio$\PageIndex{10}$

Gráfica$x=2(y-3)^{2}+2$ usando propiedades.

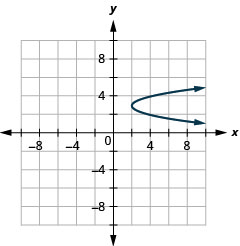
Contestar: $Esta gráfica muestra una parábola que se abre a la derecha con vértice (2, 3) y puntos simétricos (4, 2) y (4, 4).$
Figura 11.2.64

En el siguiente ejemplo, notamos que la a es negativa y así la parábola se abre hacia la izquierda.

Ejemplo$\PageIndex{6}$

Gráfica$x=-4(y+1)^{2}+4$ usando propiedades.

Solución:

Cuadro 11.2.8
	$.$
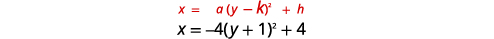Identificar las constantes$a, h, k$.	$a=-4, h=4, k=-1$
Ya que$a=-4$, la parábola se abre a la izquierda.
$.$
El eje de simetría es$y=k$.	El eje de simetría es$y=-1$.
El vértice es$(h,k)$.	El vértice es$(4,-1)$.
Encuentra la$x$ -intercepción sustituyendo$y=0$.	$x=-4(y+1)^{2}+4$ $x=-4(0+1)^{2}+4$ $x=0$
	El$x$ -intercepto es$(0,0)$.
Encuentra el punto simétrico a$(0,0)$ través del eje de simetría.	$(0,-2)$
Encuentra las$y$ -intercepciones.	$x=-4(y+1)^{2}+4$
Vamos$x=0$.	$\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}$
	$y=-1+1 \quad y=-1-1$
	$y=0 \quad\quad y=-2$
	Los$y$ -interceptos son$(0,0)$ y$(0,-2)$.
Grafica la parábola.	$.$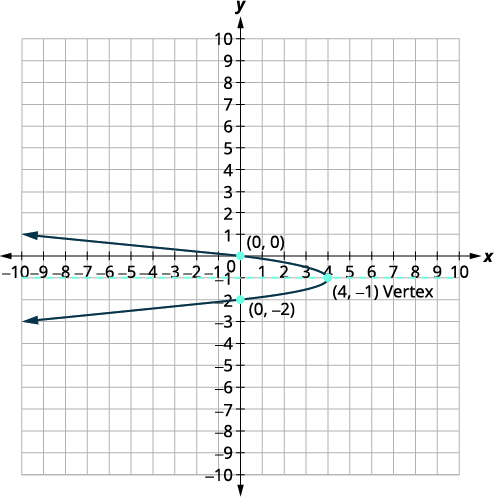

Ejercicio$\PageIndex{11}$

Gráfica$x=-4(y+2)^{2}+4$ usando propiedades.

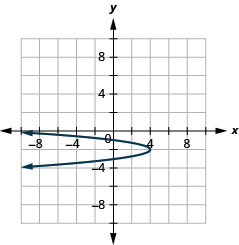
Contestar: $Esta figura muestra una parábola que se abre a la izquierda con vértice (4, negativo 2) e intercepta y (0, negativo 1) y (0, negativo 3).$
Figura 11.2.68

Ejercicio$\PageIndex{12}$

Gráfica$x=-2(y+3)^{2}+2$ usando propiedades.

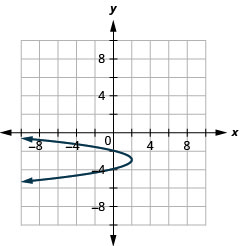
Contestar: $Esta figura muestra una parábola que se abre a la izquierda con vértice (2, negativo 3) e intercepta y (0, negativo 2) y (0, negativo 4).$
Figura 11.2.69

El siguiente ejemplo requiere que primero pongamos la ecuación en forma estándar y luego usemos las propiedades.

Ejemplo$\PageIndex{7}$

Escribe$x=2 y^{2}+12 y+17$ en forma estándar y luego usa las propiedades de la forma estándar para graficar la ecuación.

Solución:

Cuadro 11.2.9
	$x=2 y^{2}+12 y+17$
Reescribe la función en$x=a(y-k)^{2}+h$ forma completando el cuadrado.	$x=2\left(y^{2}+6 y\right)+17$
	$.$
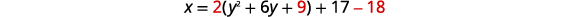	$x=2(y+3)^{2}-1$
	$.$
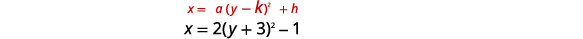Identificar las constantes$a, h, k$.	$a=2, h=-1, k=-3$
Ya que$a=2$, la parábola se abre a la derecha.
$.$
El eje de simetría es$y=k$.	El eje de simetría es$y=-3$.
El vértice es$(h,k)$.	El vértice es$(-1,-3)$.
Encuentra la$x$ -intercepción sustituyendo$y=0$.	$x=2(y+3)^{2}-1$ $x=2(0+3)^{2}-1$ $x=17$
	El$x$ -intercepto es$(17,0)$.
Encuentra el punto simétrico a$(17,0)$ través del eje de simetría.	$(17,-6)$
Encuentra las$y$ -intercepciones. Vamos$x=0$.	$\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}$
	$y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}$
	$y \approx-2.3 \quad y \approx-3.7$
	Los$y$ -interceptos son$\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)$.
Grafica la parábola.	$.$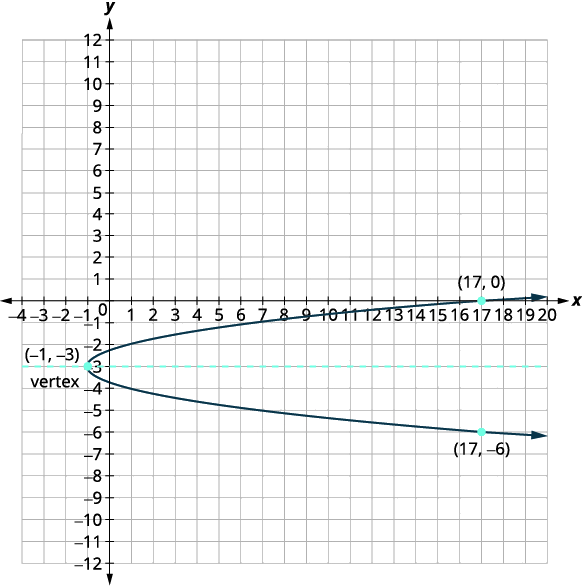

Ejercicio$\PageIndex{13}$

Escribir$x=3 y^{2}+6 y+7$ en forma estándar y
Utilice las propiedades de la forma estándar para graficar la ecuación.

Contestar

$x=3(y+1)^{2}+4$

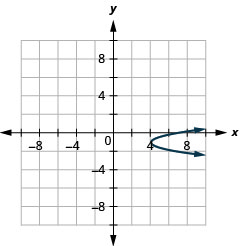
Esta gráfica muestra una parábola que se abre a la derecha con vértice (4, negativo 1) e intercepción x (7, 0). — Figura 11.2.77

Ejercicio$\PageIndex{14}$

Escribir$x=-4 y^{2}-16 y-12$ en forma estándar y
Utilice las propiedades de la forma estándar para graficar la ecuación.

Contestar

$x=-4(y+2)^{2}+4$

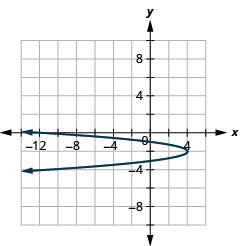
Esta gráfica muestra una parábola que se abre a la izquierda con vértice (4, negativo 2) y x intercepción menos (12, 0). — Figura 11.2.78

Resolver aplicaciones con Parabolas

Muchos diseños arquitectónicos incorporan parábolas. No es raro que los puentes se construyan usando parábolas como veremos en el siguiente ejemplo.

Ejemplo$\PageIndex{8}$

Encuentra la ecuación del arco parabólico formado en la cimentación del puente mostrado. Escribe la ecuación en forma estándar.

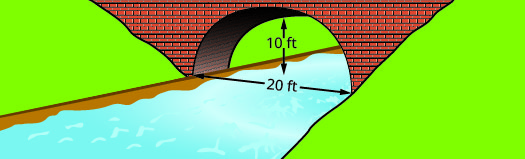
Esta figura muestra un arco parabólico formado en la cimentación de un puente. Mide 10 pies de alto y 20 pies de ancho en la base. — Figura 11.2.79

Solución:

Primero estableceremos un sistema de coordenadas y dibujaremos la parábola. La gráfica nos dará la información que necesitamos para escribir la ecuación de la gráfica en la forma estándar$y=a(x-h)^{2}+k$.

Cuadro 11.2.10
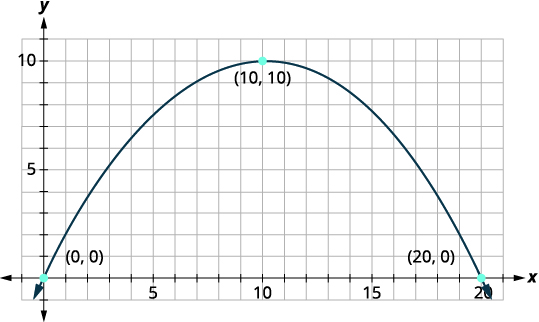Deje que el lado inferior izquierdo del puente sea el origen de la cuadrícula de coordenadas en el punto$(0,0)$. Dado que la base tiene$20$ pies de ancho el punto$(20,0)$ representa el lado inferior derecho. El puente tiene 10 pies de altura en el punto más alto. El punto más alto es el vértice de la parábola por lo que la$y$ coordenada -del vértice será$10$. Dado que el puente es simétrico, el vértice debe caer a mitad de camino entre el punto más a la izquierda$(0,0)$, y el punto más a la derecha$(20,0)$. De esto sabemos que la$x$ -coordenada del vértice también será$10$.	$.$
Identificar el vértice,$(h,k)$.	$(h, k)=(10,10)$
	$h=10, \quad k=10$
Sustituir los valores en la forma estándar. El valor de aún$a$ se desconoce. Para encontrar el valor de$a$ usar uno de los otros puntos en la parábola.	$\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}$
Sustituir los valores del otro punto en la ecuación.	$y=a(x-10)^{2}+10$ $0=a(0-10)^{2}+10$
Resolver para$a$.	$\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}$
	$y=a(x-10)^{2}+10$
Sustituir el valor para$a$ en la ecuación.	$y=-\dfrac{1}{10}(x-10)^{2}+10$

Ejercicio$\PageIndex{15}$

Encuentra la ecuación del arco parabólico formado en la cimentación del puente mostrado. Escribe la ecuación en forma estándar.

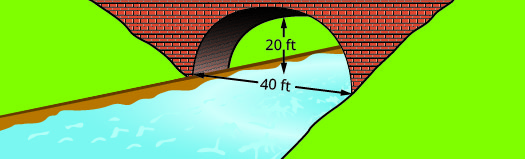
Esta figura muestra un arco parabólico formado en la cimentación de un puente. Mide 20 pies de alto y 40 pies de ancho en la base. — Figura 11.2.81

Contestar: $y=-\dfrac{1}{20}(x-20)^{2}+20$

Ejercicio$\PageIndex{16}$

Encuentra la ecuación del arco parabólico formado en la cimentación del puente mostrado. Escribe la ecuación en forma estándar.

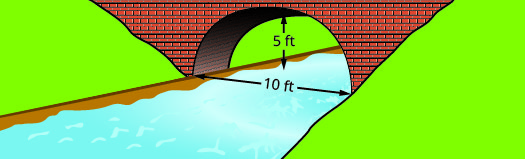
Esta figura muestra un arco parabólico formado en la cimentación de un puente. Mide 5 pies de alto y 10 pies de ancho en la base. — Figura 11.2.82

Contestar: $y=-\dfrac{1}{5} x^{2}+2 x y=-\dfrac{1}{5}(x-5)^{2}+5$

Acceda a estos recursos en línea para obtener instrucciones adicionales y practique con funciones cuadráticas y parábolas.

Funciones cuadráticas
Introducción a las Cónicas y Gráficas de Parábolas Horizontales

Conceptos clave

Parábola: Una parábola son todos los puntos en un plano que están a la misma distancia de un punto fijo y una línea fija. El punto fijo se llama foco, y la línea fija se llama directrix de la parábola.

Parabolas Verticales

Cuadro 11.2.1
	Forma general $y=a x^{2}+b x+c$	Forma estándar $y=a(x-h)^{2}+k$
Orientación	\ (y=a x^ {2} +b x+c\) ">$a>0$ arriba;$a<0$ abajo	\ (y=a (x-h) ^ {2} +k\) ">$a>0$ arriba;$a<0$ abajo
Eje de simetría	\ (y=a x^ {2} +b x+c\) ">$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k\) ">$x=h$
Vertex	\ (y=a x^ {2} +b x+c\) ">Sustituir$x=-\dfrac{b}{2 a}$ y resolver por$y .$	\ (y=a (x-h) ^ {2} +k\) ">$(h, k)$
$y$-interceptar	\ (y=a x^ {2} +b x+c\) ">Dejar$x=0$	\ (y=a (x-h) ^ {2} +k\) ">Dejar$x=0$
$x$-intercepta	\ (y=a x^ {2} +b x+c\) ">Dejar$y=0$	\ (y=a (x-h) ^ {2} +k\) ">Dejar$y=0$

Cómo graficar parábolas verticales$y=a x^{2}+b x+c$ o$f(x)=a(x-h)^{2}+k)$ usar propiedades.

Determinar si la parábola se abre hacia arriba o hacia abajo.
Encuentra el eje de simetría.
Encuentra el vértice.
Encuentra la$y$ -intercepción. Encuentra el punto simétrico a la$y$ intersección a través del eje de simetría.
Encuentra las$x$ -intercepciones.
Grafica la parábola.

Parabolas Horizontales

Cuadro 11.2.4
	Forma general $x=a y^{2}+b y+c$	Forma estándar $x=a(y-k)^{2}+h$
Orientación	\ (x=a y^ {2} +b y+c\) ">$a>0$ derecha;$a<0$ izquierda	\ (x=a (y-k) ^ {2} +h\) ">$a>0$ derecha;$a<0$ izquierda
Eje de simetría	\ (x=a y^ {2} +b y+c\) ">$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h\) ">$y=k$
Vertex	\ (x=a y^ {2} +b y+c\) ">Sustituir$y=-\dfrac{b}{2 a}$ y resolver por$x .$	\ (x=a (y-k) ^ {2} +h\) ">$(h, k)$
$x$-intercepta	\ (x=a y^ {2} +b y+c\) ">Dejar$x=0$	\ (x=a (y-k) ^ {2} +h\) ">Dejar$x=0$
$y$-interceptar	\ (x=a y^ {2} +b y+c\) ">Dejar$y=0$	\ (x=a (y-k) ^ {2} +h\) ">Dejar$y=0$

Graficando Parábolas Horizontales

Cómo graficar parábolas horizontales$x=a y^{2}+b y+c$ o$x=a(y-k)^{2}+h$ usando propiedades.

Determinar si la parábola se abre a la izquierda o a la derecha.
Encuentra el eje de simetría.
Encuentra el vértice.
Encuentra la$x$ -intercepción. Encuentra el punto simétrico a la$x$ intersección a través del eje de simetría.
Encuentra las$y$ -intercepciones.
Grafica la parábola.

Glosario

parábola: Una parábola son todos los puntos en un plano que están a la misma distancia de un punto fijo y una línea fija.

	Forma general \(y=a x^{2}+b x+c\)	Forma estándar \(y=a(x-h)^{2}+k\)
Orientación	\ (y=a x^ {2} +b x+c\) ">\(a>0\) arriba;\(a<0\) abajo	\ (y=a (x-h) ^ {2} +k\) ">\(a>0\) arriba;\(a<0\) abajo
Eje de simetría	\ (y=a x^ {2} +b x+c\) ">\(x=-\dfrac{b}{2 a}\)	\ (y=a (x-h) ^ {2} +k\) ">\(x=h\)
Vertex	\ (y=a x^ {2} +b x+c\) ">Sustituir\(x=-\dfrac{b}{2 a}\) y resolver por\(y .\)	\ (y=a (x-h) ^ {2} +k\) ">\((h, k)\)
\(y\)-interceptar	\ (y=a x^ {2} +b x+c\) ">Dejar\(x=0\)	\ (y=a (x-h) ^ {2} +k\) ">Dejar\(x=0\)
\(x\)-intercepta	\ (y=a x^ {2} +b x+c\) ">Dejar\(y=0\)	\ (y=a (x-h) ^ {2} +k\) ">Dejar\(y=0\)

	\( \begin{align} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt] \color{black}{y} &=-x^{2}+6 x-8 \end{align}\)
Ya que\(a\) es\(-1\), la parábola se abre hacia abajo.
$.$
Para encontrar el eje de simetría, encontrar\(x=-\dfrac{b}{2 a}\).	\( \begin{align} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align}\)
	El eje de simetría es\(x=3\).
	$.$
El vértice está en la línea\(x=3\).	\(y=-x^{2}+6 x-8\)
Vamos\(x=3\).	$.$
	\(\begin{align} y &=-9+18-8 \\[4pt] y &=1 \end{align}\)
	El vértice es\((3,1)\).
	$.$
La\(y\) -intercepción ocurre cuando\(x=0\).	\(y=-x^{2}+6 x-8\)
Sustituto\(x=0\).	\(y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8\)
Simplificar.	\(y=-8\)
	El\(y\) -intercepto es\((0,-8)\).
El punto\((0,−8)\) está a tres unidades a la izquierda de la línea de simetría. El punto tres unidades a la derecha de la línea de simetría es\((6,−8)\).	Punto simétrico a la\(y\) -intercepción es\((6,−8)\).
	$.$
La\(x\) -intercepción ocurre cuando\(y=0\).	\(y=-x^{2}+6 x-8\)
Vamos\(y=0\).	\(\color{red}{0} \color{black}{=}-x^{2}+6 x-8\)
Factivar el GCF.	\(0=-\left(x^{2}-6 x+8\right)\)
Factorial el trinomio.	\(0=-(x-4)(x-2)\)
Resolver para\(x\).	\(x=4, \quad x=2\)
	Los\(x\) -interceptos son\((4,0),(2,0)\).
Grafica la parábola.	$.$

Reescribe la función en\(y=a(x-h)^{2}+k\) forma completando el cuadrado.	\(\begin{align} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3 \\[4pt] y &=3(x-1)^{2}+2 \end{align}\)
Identificar las constantes\(a, h, k\).	\(a=3, h=1, k=2\)
Ya que\(a=2\), la parábola se abre hacia arriba.
$.$
El eje de simetría es\(x=h\).	El eje de simetría es\(x=1\).
El vértice es\((h,k)\).	El vértice es\((1,2)\).
Encuentra la\(y\) -intercepción sustituyendo\(x=0\),	\( \begin{align} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align} \)
	\(y\)-interceptar\((0,5)\)
Encuentra el punto simétrico a\((0,5)\) través del eje de simetría.	\((2,5)\)
Encuentra las\(x\) -intercepciones.	\(\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}\)
	La raíz cuadrada de un número negativo nos dice que las soluciones son números complejos. Entonces no hay\(x\) -intercepciones.
Grafica la parábola.	$.$

	Forma general \(x=a y^{2}+b y+c\)	Forma estándar \(x=a(y-k)^{2}+h\)
Orientación	\ (x=a y^ {2} +b y+c\) ">\(a>0\) derecha;\(a<0\) izquierda	\ (x=a (y-k) ^ {2} +h\) ">\(a>0\) derecha;\(a<0\) izquierda
Eje de simetría	\ (x=a y^ {2} +b y+c\) ">\(y=-\dfrac{b}{2 a}\)	\ (x=a (y-k) ^ {2} +h\) ">\(y=k\)
Vertex	\ (x=a y^ {2} +b y+c\) ">Sustituir\(y=-\dfrac{b}{2 a}\) y resolver por\(x .\)	\ (x=a (y-k) ^ {2} +h\) ">\((h, k)\)
\(x\)-intercepta	\ (x=a y^ {2} +b y+c\) ">Dejar\(x=0\)	\ (x=a (y-k) ^ {2} +h\) ">Dejar\(x=0\)
\(y\)-interceptar	\ (x=a y^ {2} +b y+c\) ">Dejar\(y=0\)	\ (x=a (y-k) ^ {2} +h\) ">Dejar\(y=0\)

	$.$
Ya que\(a=2\), la parábola se abre a la derecha.
$.$
Para encontrar el eje de simetría, encontrar\(y=-\dfrac{b}{2 a}\)	\(y=-\dfrac{b}{2 a}\)
	\(y=-\dfrac{0}{2(2)}\)
	\(y=0\)
	El eje de simetría es\(y=0\).
El vértice está en la línea\(y=0\).	\(x=2 y^{2}\)
Vamos\(y=0\).	$.$
	\(x=0\)
	El vértice es\((0,0)\).

Search

Text Color

Text Size

Margin Size

Font Type

Definición\(\PageIndex{1}\): Parabola, Focus, and Directrix

Graficando Parábolas Verticales

Ejemplo\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Cómo: Gráfica Parábolas Horizontales\(y=a x^{2}+b x+c\) or \(f(x)=a(x-h)^{2}+k\) using Properties

Ejemplo\(\PageIndex{3}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejemplo\(\PageIndex{4}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejemplo\(\PageIndex{5}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejemplo\(\PageIndex{6}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejemplo\(\PageIndex{7}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejemplo\(\PageIndex{8}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Graficando Parábolas Horizontales

	$.$
Ya que\(a=-1\), la parábola se abre a la izquierda.
$.$
Para encontrar el eje de simetría, encontrar\(y=-\dfrac{b}{2 a}\)	\(y=-\dfrac{b}{2 a}\)
	\(y=-\dfrac{2}{2(-1)}\)
	\(y=1\)
	El eje de simetría es\(y=1\).
El vértice está en la línea\(y=1\).	\(x=-y^{2}+2 y+8\)
Vamos\(y=1\).	$.$
	\(x=9\)
	El vértice es\((9,1)\).
La\(x\) -intercepción ocurre cuando\(y=0\).	\(x=-y^{2}+2 y+8\)
	$.$
	\(x=8\)
	El\(x\) -intercepto es\((8,0)\).
El punto\((8,0)\) es una unidad por debajo de la línea de simetría. El punto simétrico una unidad por encima de la línea de simetría es\((8,2)\)	El punto simétrico es\((8,2)\).
La\(y\) -intercepción ocurre cuando\(x=0\).	\(x=-y^{2}+2 y+8\)
Sustituto\(x=0\).	\(0=-y^{2}+2 y+8\)
Resolver.	\(y^{2}-2 y-8=0\)
	\((y-4)(y+2)=0\)
	\(y=4, \quad y=-2\)
	Los\(y\) -interceptos son\((0,4)\) y\((0,-2)\).
Conecta los puntos para graficar la parábola.	$.$

	$.$
Identificar las constantes\(a, h, k\).	\(a=2, h=1, k=2\)
Ya que\(a=2\), la parábola se abre a la derecha.
$.$
El eje de simetría es\(y=k\).	El eje de simetría es\(y=2\).
El vértice es\((h,k)\).	El vértice es\((1,2)\).
Encuentra la\(x\) -intercepción sustituyendo\(y=0\).	\(x=2(y-2)^{2}+1\) \(x=2(0-2)^{2}+1\) \(x=9\)
	El\(x\) -intercepto es\((9,0)\).
Encuentra el punto simétrico a\((9,0)\) través del eje de simetría.	\((9,4)\)
Encuentra las\(y\) -intercepciones. Vamos\(x=0\).	\(\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}\)
	Un cuadrado no puede ser negativo, por lo que no hay una solución real. Entonces no hay\(y\) -intercepciones.
Grafica la parábola.	$.$

	$.$
Identificar las constantes\(a, h, k\).	\(a=-4, h=4, k=-1\)
Ya que\(a=-4\), la parábola se abre a la izquierda.
$.$
El eje de simetría es\(y=k\).	El eje de simetría es\(y=-1\).
El vértice es\((h,k)\).	El vértice es\((4,-1)\).
Encuentra la\(x\) -intercepción sustituyendo\(y=0\).	\(x=-4(y+1)^{2}+4\) \(x=-4(0+1)^{2}+4\) \(x=0\)
	El\(x\) -intercepto es\((0,0)\).
Encuentra el punto simétrico a\((0,0)\) través del eje de simetría.	\((0,-2)\)
Encuentra las\(y\) -intercepciones.	\(x=-4(y+1)^{2}+4\)
Vamos\(x=0\).	\(\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}\)
	\(y=-1+1 \quad y=-1-1\)
	\(y=0 \quad\quad y=-2\)
	Los\(y\) -interceptos son\((0,0)\) y\((0,-2)\).
Grafica la parábola.	$.$

	\(x=2 y^{2}+12 y+17\)
Reescribe la función en\(x=a(y-k)^{2}+h\) forma completando el cuadrado.	\(x=2\left(y^{2}+6 y\right)+17\)
	$.$
	\(x=2(y+3)^{2}-1\)
	$.$
Identificar las constantes\(a, h, k\).	\(a=2, h=-1, k=-3\)
Ya que\(a=2\), la parábola se abre a la derecha.
$.$
El eje de simetría es\(y=k\).	El eje de simetría es\(y=-3\).
El vértice es\((h,k)\).	El vértice es\((-1,-3)\).
Encuentra la\(x\) -intercepción sustituyendo\(y=0\).	\(x=2(y+3)^{2}-1\) \(x=2(0+3)^{2}-1\) \(x=17\)
	El\(x\) -intercepto es\((17,0)\).
Encuentra el punto simétrico a\((17,0)\) través del eje de simetría.	\((17,-6)\)
Encuentra las\(y\) -intercepciones. Vamos\(x=0\).	\(\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}\)
	\(y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}\)
	\(y \approx-2.3 \quad y \approx-3.7\)
	Los\(y\) -interceptos son\(\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)\).
Grafica la parábola.	$.$

Deje que el lado inferior izquierdo del puente sea el origen de la cuadrícula de coordenadas en el punto\((0,0)\). Dado que la base tiene\(20\) pies de ancho el punto\((20,0)\) representa el lado inferior derecho. El puente tiene 10 pies de altura en el punto más alto. El punto más alto es el vértice de la parábola por lo que la\(y\) coordenada -del vértice será\(10\). Dado que el puente es simétrico, el vértice debe caer a mitad de camino entre el punto más a la izquierda\((0,0)\), y el punto más a la derecha\((20,0)\). De esto sabemos que la\(x\) -coordenada del vértice también será\(10\).	$.$
Identificar el vértice,\((h,k)\).	\((h, k)=(10,10)\)
	\(h=10, \quad k=10\)
Sustituir los valores en la forma estándar. El valor de aún\(a\) se desconoce. Para encontrar el valor de\(a\) usar uno de los otros puntos en la parábola.	\(\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}\)
Sustituir los valores del otro punto en la ecuación.	\(y=a(x-10)^{2}+10\) \(0=a(0-10)^{2}+10\)
Resolver para\(a\).	\(\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}\)
	\(y=a(x-10)^{2}+10\)
Sustituir el valor para\(a\) en la ecuación.	\(y=-\dfrac{1}{10}(x-10)^{2}+10\)