11.5: Secciones Cónicas
- Page ID
- 116190
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identificar la ecuación de una parábola en forma estándar con enfoque y directrix dados.
- Identificar la ecuación de una elipse en forma estándar con focos dados.
- Identificar la ecuación de una hipérbola en forma estándar con focos dados.
- Reconocer una parábola, elipse o hipérbola a partir de su valor de excentricidad.
- Escribe la ecuación polar de una sección cónica con excentricidad\(e\).
- Identificar cuando una ecuación general de grado dos es una parábola, elipse o hipérbola.
Las secciones cónicas se han estudiado desde la época de los antiguos griegos, y se consideraron un concepto matemático importante. Ya en el 320 a. C., matemáticos griegos como Menaechmus, Appollonius y Arquímedes quedaron fascinados por estas curvas. Appollonius escribió un tratado completo de ocho volúmenes sobre secciones cónicas en el que, por ejemplo, era capaz de derivar un método específico para identificar una sección cónica mediante el uso de la geometría. Desde entonces, han surgido importantes aplicaciones de secciones cónicas (por ejemplo, en astronomía), y las propiedades de las secciones cónicas se utilizan en radiotelescopios, receptores de antena parabólica e incluso arquitectura. En esta sección discutimos las tres secciones cónicas básicas, algunas de sus propiedades y sus ecuaciones.
Las secciones cónicas obtienen su nombre porque se pueden generar cruzando un plano con un cono. Un cono tiene dos partes de forma idéntica llamadas nappes. Un nappe es lo que la mayoría de la gente quiere decir con “cono”, que tiene la forma de un sombrero de fiesta. Se puede generar un cono circular derecho girando una línea que pasa por el origen alrededor del eje y como se muestra en la Figura\(\PageIndex{1}\).
Las secciones cónicas son generadas por la intersección de un plano con un cono (Figura\(\PageIndex{2}\)). Si el plano es paralelo al eje de revolución (el eje y), entonces la sección cónica es una hipérbola. Si el plano es paralelo a la línea generadora, la sección cónica es una parábola. Si el plano es perpendicular al eje de revolución, la sección cónica es un círculo. Si el plano se cruza con un nappe en ángulo con el eje (distinto de
Parábolas
Se genera una parábola cuando un plano cruza un cono paralelo a la línea generadora. En este caso, el avión cruza sólo una de las siestas. Una parábola también se puede definir en términos de distancias.
Una parábola es el conjunto de todos los puntos cuya distancia desde un punto fijo, llamado foco, es igual a la distancia desde una línea fija, llamada directriz. El punto a medio camino entre el foco y la directrix se llama el vértice de la parábola.
Una gráfica de una parábola típica aparece en la Figura\(\PageIndex{3}\). Usando este diagrama en conjunto con la fórmula de distancia, podemos derivar una ecuación para una parábola. Recordemos la fórmula de distancia: Dado el punto P con coordenadas\((x_1,y_1)\) y el punto Q con coordenadas\((x_2,y_2),\) la distancia entre ellos viene dada por la fórmula
\[d(P,Q)=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
Luego de la definición de una parábola y Figura\(\PageIndex{3}\), obtenemos
\[d(F,P)=d(P,Q) \nonumber \]
\[\sqrt{(0−x)^2+(p−y)^2}=\sqrt{(x−x)^2+(−p−y)^2}. \nonumber \]
Cuadrando ambos lados y simplificando los rendimientos
\[ \begin{align} x^2+(p−y)^2 = 0^2+(−p−y)^2 \\ x^2+p^2−2py+y^2 = p^2+2py+y^2 \\ x^2−2py =2py \\ x^2 =4py. \end{align} \nonumber \]
Ahora supongamos que queremos reubicar el vértice. Utilizamos las variables\((h,k)\) para denotar las coordenadas del vértice. Entonces si el foco está directamente por encima del vértice, tiene coordenadas\((h,k+p)\) y la directrix tiene la ecuación\(y=k−p\). Al pasar por la misma derivación se obtiene la fórmula\((x−h)^2=4p(y−k)\). Resolver esta ecuación para\(y\) lleva al siguiente teorema.
Dada una parábola que se abre hacia arriba con el vértice ubicado en\((h,k)\) y el foco ubicado en\((h,k+p)\), donde\(p\) es una constante, la ecuación para la parábola viene dada por
\[y=\dfrac{1}{4p}(x−h)^2+k. \nonumber \]
Esta es la forma estándar de una parábola.
También podemos estudiar los casos en que la parábola se abre hacia abajo o hacia la izquierda o hacia la derecha. La ecuación para cada uno de estos casos también se puede escribir en forma estándar como se muestra en las siguientes gráficas.
Además, la ecuación de una parábola se puede escribir en la forma general, aunque en esta forma los valores de\(h\),\(k\), y no\(p\) son inmediatamente reconocibles. La forma general de una parábola está escrita como
\[ax^2+bx+cy+d=0 \label{para1} \]
o
\[ay^2+bx+cy+d=0.\label{para2} \]
La ecuación\ ref {para1} representa una parábola que se abre hacia arriba o hacia abajo. La ecuación\ ref {para2} representa una parábola que se abre ya sea a la izquierda o a la derecha. Para poner la ecuación en forma estándar, utilice el método de completar el cuadrado.
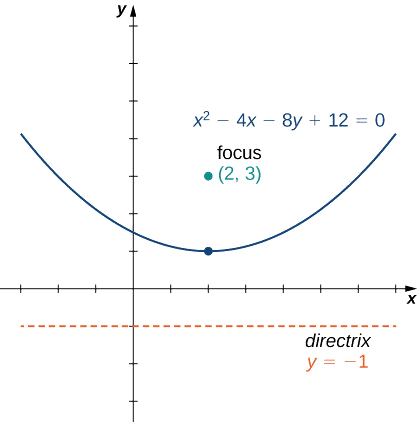
Poner la ecuación
\[x^2−4x−8y+12=0 \nonumber \]
en forma estándar y grafica la parábola resultante.
Solución
Dado que y no está al cuadrado en esta ecuación, sabemos que la parábola se abre ya sea hacia arriba o hacia abajo. Por lo tanto, necesitamos resolver esta ecuación para y, que pondrá la ecuación en forma estándar. Para hacer eso, primero agregue\(8y\) a ambos lados de la ecuación:
\[8y=x^2−4x+12. \nonumber \]
El siguiente paso es completar el cuadrado en el lado derecho. Comience agrupando los dos primeros términos en el lado derecho usando paréntesis:
\[8y=(x^2−4x)+12. \nonumber \]
A continuación determinar la constante que, cuando se agrega dentro de los paréntesis, hace que la cantidad dentro de los paréntesis sea un trinomio cuadrado perfecto. Para ello, toma la mitad del coeficiente de x y cuadrázala. Esto da a\((\dfrac{−4}{2})^2=4.\) Sumar 4 dentro de los paréntesis y restar 4 fuera de los paréntesis, por lo que no se cambia el valor de la ecuación:
\[8y=(x^2−4x+4)+12−4. \nonumber \]
Ahora combine términos similares y factifique la cantidad dentro de los paréntesis:
\[8y=(x−2)^2+8. \nonumber \]
Por último, dividir por 8:
\[y=\dfrac{1}{8}(x−2)^2+1. \nonumber \]
Esta ecuación se encuentra ahora en forma estándar. Comparando esto con la ecuación da\(h=2, k=1\), y\(p=2\). La parábola se abre, con vértice en\((2,1)\), enfoque y directrix\(y=−1\).\((2,3)\) La gráfica de esta parábola aparece de la siguiente manera.
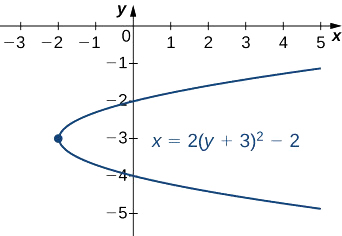
Poner la ecuación\(2y^2−x+12y+16=0\) en forma estándar y graficar la parábola resultante.
- Pista
-
Resolver para\(x\). Comprueba en qué dirección se abre la parábola.
- Contestar
-
\[x=2(y+3)^2−2 \nonumber \]
El eje de simetría de una parábola vertical (apertura hacia arriba o hacia abajo) es una línea vertical que pasa por el vértice. La parábola tiene una interesante propiedad reflectante. Supongamos que tenemos una antena parabólica con sección transversal parabólica. Si un haz de ondas electromagnéticas, como la luz o las ondas de radio, entra en el plato en línea recta desde un satélite (paralelo al eje de simetría), entonces las ondas se reflejan en el plato y se recogen en el foco de la parábola como se muestra.
Considera una antena parabólica diseñada para recoger señales de un satélite en el espacio. El plato está dirigido directamente al satélite, y un receptor se ubica en el foco de la parábola. Las ondas de radio que llegan desde el satélite se reflejan desde la superficie de la parábola hacia el receptor, que recoge y decodifica las señales digitales. Esto permite que un pequeño receptor recoja señales desde un gran ángulo de cielo. Las linternas y los faros de un automóvil funcionan según el mismo principio, pero a la inversa: la fuente de la luz (es decir, la bombilla) se ubica en el foco y la superficie reflectante en el espejo parabólico enfoca el haz en línea recta. Esto permite que una pequeña bombilla ilumine un gran ángulo de espacio frente a la linterna o automóvil.
Elipses
Una elipse también se puede definir en términos de distancias. En el caso de una elipse, hay dos focos (plural de foco), y dos directrices (plural de directrix). Analizamos las instrucciones con más detalle más adelante en esta sección.
Una elipse es el conjunto de todos los puntos para los cuales la suma de sus distancias desde dos puntos fijos (los focos) es constante.
En la Figura se muestra una gráfica de una elipse típica\(\PageIndex{6}\). En esta figura los focos están etiquetados como\(F\) y\(F′\). Ambos tienen la misma distancia fija desde el origen, y esta distancia está representada por la variable\(c\). Por lo tanto las coordenadas de\(F\) son\((c,0)\) y las coordenadas de\(F′\) son\((−c,0).\) Los puntos\(P\) y\(P′\) se localizan en los extremos del eje mayor de la elipse, y tienen coordenadas\((a,0)\) y\((−a,0)\), respectivamente. El eje mayor es siempre la distancia más larga a través de la elipse, y puede ser horizontal o vertical. Así, la longitud del eje mayor en esta elipse es\(2a\). Además,\(P\) y\(P′\) se llaman los vértices de la elipse. Los puntos\(Q\) y\(Q′\) están ubicados en los extremos del eje menor de la elipse, y tienen coordenadas\((0,b)\) y\((0,−b),\) respectivamente. El eje menor es la distancia más corta a través de la elipse. El eje menor es perpendicular al eje mayor.
Según la definición de la elipse, podemos elegir cualquier punto de la elipse y la suma de las distancias desde este punto a los dos focos es constante. Supongamos que elegimos el punto\(P\). Dado que las coordenadas de punto\(P\) son\((a,0),\) la suma de las distancias es
\[d(P,F)+d(P,F′)=(a−c)+(a+c)=2a. \nonumber \]
Por lo tanto, la suma de las distancias desde un punto arbitrario A con coordenadas también\((x,y)\) es igual a\(2a\). Usando la fórmula de distancia, obtenemos
\[d(A,F)+d(A,F′)=2a. \nonumber \]
\[\sqrt{(x−c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a \nonumber \]
Restar el segundo radical de ambos lados y cuadrar ambos lados:
\[\sqrt{(x−c)^2+y^2}=2a−\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Ahora aísle el radical en el lado derecho y vuelva a cuadrar:
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx \nonumber \]
\[4a\sqrt{(x+c)^2+y^2}=4a^2+4cx \nonumber \]
\[\sqrt{(x+c)^2+y^2}=a+\dfrac{cx}{a} \nonumber \]
\[(x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}. \nonumber \]
Aísle las variables en el lado izquierdo de la ecuación y las constantes en el lado derecho:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Divide ambos lados por\(a^2−c^2\). Esto da la ecuación
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Si nos referimos de nuevo a Figura\(\PageIndex{6}\), entonces la longitud de cada uno de los dos segmentos de línea verde es igual a\(a\). Esto es cierto porque la suma de las distancias desde el punto\(Q\) a los focos\(F\) y\(F′\) es igual a\(2a\), y las longitudes de estos dos segmentos de línea son iguales. Este segmento de línea forma un triángulo rectángulo con longitud de hipotenusa\(a\) y longitudes de pierna\(b\) y\(c\). Del teorema de Pitágoras,\(b^2+c^2=a^2\) y\(b^2=a^2−c^2\). Por lo tanto, la ecuación de la elipse se convierte
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1. \nonumber \]
Finalmente, si el centro de la elipse se mueve del origen a un punto\((h,k)\), tenemos la siguiente forma estándar de elipse.
Considera la elipse con centro\((h,k)\), un eje mayor horizontal con longitud\(2a\) y un eje menor vertical con longitud\(2b\). Entonces la ecuación de esta elipse en forma estándar es
\[\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1 \label{HorEllipse} \]
y los focos se encuentran en\((h±c,k)\), donde\(c^2=a^2−b^2\). Las ecuaciones de las lineas son\(x=h±\dfrac{a^2}{c}\).
Si el eje mayor es vertical, entonces la ecuación de la elipse se convierte en
\[\dfrac{(x−h)^2}{b^2}+\dfrac{(y−k)^2}{a^2}=1 \label{VertEllipse} \]
y los focos se encuentran en\((h,k±c)\), donde\(c^2=a^2−b^2\). Las ecuaciones de las instrucciones en este caso son\(y=k±\dfrac{a^2}{c}\).
Si el eje mayor es horizontal, entonces la elipse se llama horizontal, y si el eje mayor es vertical, entonces la elipse se llama vertical. La ecuación de una elipse está en forma general si está en la forma
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
donde A y B son ambos positivos o ambos negativos. Para convertir la ecuación de forma general a forma estándar, utilice el método de completar el cuadrado.
Poner la ecuación
\[9x^2+4y^2−36x+24y+36=0 \nonumber \]
en forma estándar y grafica la elipse resultante.
Solución
Primero resta 36 de ambos lados de la ecuación:
\[9x^2+4y^2−36x+24y=−36. \nonumber \]
A continuación,\(x\) agrupe los términos y los\(y\) términos juntos, y factorizar el factor común:
\[(9x^2−36x)+(4y^2+24y)=−36 \nonumber \]
\[9(x^2−4x)+4(y^2+6y)=−36. \nonumber \]
Necesitamos determinar la constante que, cuando se agrega dentro de cada conjunto de paréntesis, da como resultado un cuadrado perfecto. En el primer conjunto de paréntesis, tomar la mitad del coeficiente de x y cuadrarlo. Esto da\((\dfrac{−4}{2})^2=4.\) En el segundo conjunto de paréntesis, tomar la mitad del coeficiente de y y cuadrarlo. Esto da a\((\dfrac{6}{2})^2=9.\) Agregar estos dentro de cada par de paréntesis. Dado que el primer conjunto de paréntesis tiene un 9 al frente, en realidad estamos agregando 36 al lado izquierdo. De igual manera, también estamos sumando 36 al segundo set. Por lo tanto la ecuación se convierte
\[9(x^2−4x+4)+4(y^2+6y+9)=−36+36+36 \nonumber \]
\[9(x^2−4x+4)+4(y^2+6y+9)=36. \nonumber \]
Ahora factoriza ambos conjuntos de paréntesis y divídalo por 36:
\[9(x−2)^2+4(y+3)^2=36 \nonumber \]
\[\dfrac{9(x−2)^2}{36}+\dfrac{4(y+3)^2}{36}=1 \nonumber \]
\[\dfrac{(x−2)^2}{4}+\dfrac{(y+3)^2}{9}=1. \nonumber \]
La ecuación se encuentra ahora en forma estándar. Comparando esto con la ecuación\ ref {vertellipse} da\(h=2, k=−3, a=3,\) y\(b=2\). Se trata de una elipse vertical con centro en\((2,−3)\), eje mayor 6 y eje menor 4. La gráfica de esta elipse aparece de la siguiente manera.

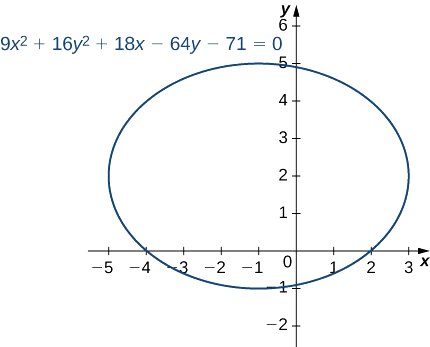
Poner la ecuación
\[9x^2+16y^2+18x−64y−71=0 \nonumber \]
en forma estándar y grafica la elipse resultante.
- Pista
-
Mueva la constante y complete el cuadrado.
- Contestar
-
\[\dfrac{(x+1)^2}{16}+\dfrac{(y−2)^2}{9}=1 \nonumber \]
Según la primera ley de movimiento planetario de Kepler, la órbita de un planeta alrededor del Sol es una elipse con el Sol en uno de los focos como se muestra en la Figura\(\PageIndex{8A}\). Debido a que la órbita de la Tierra es una elipse, la distancia al Sol varía a lo largo del año. Un concepto erróneo comúnmente sostenido es que la Tierra está más cerca del Sol en el verano. De hecho, en verano para el hemisferio norte, la Tierra está más lejos del Sol que durante el invierno. La diferencia en la estación es causada por la inclinación del eje de la Tierra en el plano orbital. Los cometas que orbitan el Sol, como el cometa Halley, también tienen órbitas elípticas, al igual que las lunas que orbitan los planetas y los satélites que orbitan la Tierra.
Las elipses también tienen interesantes propiedades reflectantes: Un rayo de luz que emana de un foco pasa a través del otro foco después de la reflexión especular en la elipse. Lo mismo ocurre con una onda de sonido también. El Salón Nacional de Estatuas en el Capitolio de Estados Unidos en Washington, DC, es una famosa sala en forma elíptica como se muestra en la Figura\(\PageIndex{8B}\). Este salón sirvió como lugar de encuentro para la Cámara de Representantes de Estados Unidos durante casi cincuenta años. La ubicación de los dos focos de esta habitación semielíptica se identifican claramente por marcas en el piso, e incluso si la habitación está llena de visitantes, cuando dos personas se paran en estos lugares y se hablan entre sí, pueden escucharse mucho más claramente de lo que pueden escuchar a alguien parado cerca. Cuenta la leyenda que John Quincy Adams tenía su escritorio ubicado en uno de los focos y pudo escuchar a todos los demás en la Casa sin necesidad de ponerse de pie. Si bien esto hace una buena historia, es poco probable que sea verdad, porque el techo original produjo tantos ecos que toda la habitación tuvo que ser colgada con alfombras para amortiguar el ruido. El techo fue reconstruido en 1902 y sólo entonces surgió el ahora famoso efecto susurrante. Otra famosa galería susurrante, el sitio de muchas propuestas de matrimonio, se encuentra en la estación Grand Central de la ciudad de Nueva York.
Hipérbolas
Una hipérbola también se puede definir en términos de distancias. En el caso de una hipérbola, hay dos focos y dos pautas. Las hipérbolas también tienen dos asíntotas.
Una hipérbola es el conjunto de todos los puntos donde la diferencia entre sus distancias desde dos puntos fijos (los focos) es constante.
Una gráfica de una hipérbola típica aparece de la siguiente manera.
La derivación de la ecuación de una hipérbola en forma estándar es prácticamente idéntica a la de una elipse. Un ligero enganche radica en la definición: La diferencia entre dos números siempre es positiva. Dejar\(P\) ser un punto sobre la hipérbola con coordenadas\((x,y)\). Entonces la definición de la hipérbola da\(|d(P,F_1)−d(P,F_2)|=constant\). Para simplificar la derivación, supongamos que\(P\) está en la rama derecha de la hipérbola, por lo que caen las barras de valor absoluto. Si está en la rama izquierda, entonces se invierte la resta. El vértice de la rama derecha tiene coordenadas\((a,0),\) así
\[d(P,F_1)−d(P,F_2)=(c+a)−(c−a)=2a. \nonumber \]
Por lo tanto, esta ecuación es cierta para cualquier punto de la hipérbola. Volviendo a las coordenadas\((x,y)\) para\(P\):
\[d(P,F_1)−d(P,F_2)=2a \nonumber \]
\[\sqrt{(x+c)^2+y^2}−\sqrt{(x−c)^2+y^2}=2a. \nonumber \]
Aísle el segundo radical y cuadre ambos lados:
\[\sqrt{(x−c)^2+y^2}=-2a+\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Ahora aísle el radical en el lado derecho y vuelva a cuadrar:
\(−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx\)
\(-4a\sqrt{(x+c)^2+y^2}=−4a^2−4cx\)
\(-\sqrt{(x+c)^2+y^2}=−a−\dfrac{cx}{a}\)
\((x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}\).
Aísle las variables en el lado izquierdo de la ecuación y las constantes en el lado derecho:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Por último, dividir ambos lados por\(a^2−c^2\). Esto da la ecuación
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Ahora definimos b para que\(b^2=c^2−a^2\). Esto es posible porque\(c>a\). Por lo tanto, la ecuación de la hipérbola se convierte
\[\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1. \nonumber \]
Finalmente, si el centro de la hipérbola se mueve del origen al punto\((h,k),\) tenemos la siguiente forma estándar de una hipérbola.
Considere la hipérbola con centro\((h,k)\), un eje mayor horizontal y un eje menor vertical. Entonces la ecuación de esta hipérbola es
\[\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1 \label{HorHyperbola} \]
y los focos se localizan en\((h±c,k),\) donde\(c^2=a^2+b^2\). Las ecuaciones de las asíntotas vienen dadas por\(y=k±\dfrac{b}{a}(x−h).\) Las ecuaciones de las pautas son
\[x=h±\dfrac{a^2}{\sqrt{a^2+b^2}}=h±\dfrac{a^2}{c} \nonumber \]
Si el eje mayor es vertical, entonces la ecuación de la hipérbola se convierte
\[\dfrac{(y−k)^2}{a^2}−\dfrac{(x−h)^2}{b^2}=1 \nonumber \]
y los focos se localizan en\((h,k±c),\) donde\(c^2=a^2+b^2\). Las ecuaciones de las asíntotas vienen dadas por\(y=k±\dfrac{a}{b}(x−h)\). Las ecuaciones de las directriz son
\[y=k±\dfrac{a^2}{\sqrt{a^2+b^2}}=k±\dfrac{a^2}{c}. \nonumber \]
Si el eje mayor (eje transversal) es horizontal, entonces la hipérbola se llama horizontal, y si el eje mayor es vertical entonces la hipérbola se llama vertical. La ecuación de una hipérbola está en forma general si está en la forma
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
donde A y B tienen signos opuestos. Para convertir la ecuación de forma general a forma estándar, utilice el método de completar el cuadrado.
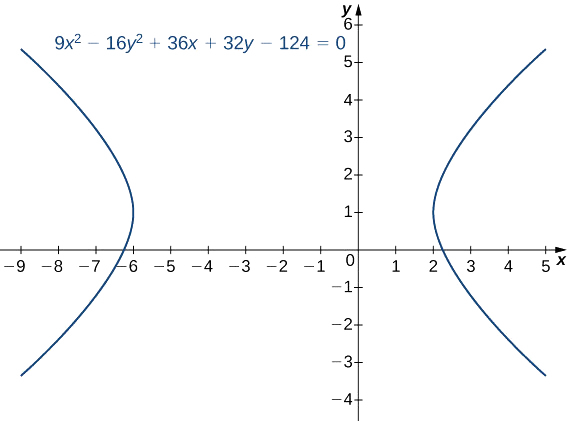
Poner la ecuación\(9x^2−16y^2+36x+32y−124=0\) en forma estándar y graficar la hipérbola resultante. ¿Cuáles son las ecuaciones de las asíntotas?
Solución
Primero agregue 124 a ambos lados de la ecuación:
\(9x^2−16y^2+36x+32y=124.\)
A continuación agrupa los términos x y los términos y juntos, luego factorizar los factores comunes:
\((9x^2+36x)−(16y^2−32y)=124\)
\(9(x^2+4x)−16(y^2−2y)=124\).
Necesitamos determinar la constante que, cuando se agrega dentro de cada conjunto de paréntesis, da como resultado un cuadrado perfecto. En el primer conjunto de paréntesis, tomar la mitad del coeficiente de x y cuadrarlo. Esto da\((\dfrac{4}{2})^2=4\). En el segundo conjunto de paréntesis, tomar la mitad del coeficiente de y y cuadrarlo. Esto da a\((\dfrac{−2}{2})^2=1.\) Agregar estos dentro de cada par de paréntesis. Dado que el primer conjunto de paréntesis tiene un 9 al frente, en realidad estamos agregando 36 al lado izquierdo. De igual manera, estamos restando 16 del segundo conjunto de paréntesis. Por lo tanto la ecuación se convierte
\(9(x^2+4x+4)−16(y^2−2y+1)=124+36−16\)
\(9(x^2+4x+4)−16(y^2−2y+1)=144.\)
Siguiente factor ambos conjuntos de paréntesis y dividir por 144:
\(9(x+2)^2−16(y−1)^2=144\)
\(\dfrac{9(x+2)^2}{144}−\dfrac{16(y−1)^2}{144}=1\)
\(\dfrac{(x+2)^2}{16}−\dfrac{(y−1)^2}{9}=1.\)
La ecuación se encuentra ahora en forma estándar. Comparando esto con la Ecuación\ ref {HorHyperbola} da\(h=−2, k=1, a=4,\) y\(b=3\). Se trata de una hipérbola horizontal con centro en\((−2,1)\) y asíntotas dadas por las ecuaciones\(y=1±\dfrac{3}{4}(x+2)\). La gráfica de esta hipérbola aparece en la Figura\(\PageIndex{10}\).
Poner la ecuación\(4y^2−9x^2+16y+18x−29=0\) en forma estándar y graficar la hipérbola resultante. ¿Cuáles son las ecuaciones de las asíntotas?
- Pista
-
Mueva la constante y complete el cuadrado. Comprueba en qué dirección se abre la hipérbola
- Contestar
-
\(\dfrac{(y+2)^2}{9}−\dfrac{(x−1)^2}{4}=1.\)Se trata de una hipérbola vertical. asíntotas\(y=−2±\dfrac{3}{2}(x−1).\)

Las hipérbolas también tienen interesantes propiedades reflectantes. Un rayo dirigido hacia un foco de una hipérbola es reflejado por un espejo hiperbólico hacia el otro foco. Este concepto se ilustra en la Figura\(\PageIndex{11}\).
Esta propiedad de la hipérbola tiene importantes aplicaciones. Se utiliza en la búsqueda de dirección de radio (ya que la diferencia en las señales de dos torres es constante a lo largo de las hipérbolas), y en la construcción de espejos dentro de telescopios (para reflejar la luz proveniente del espejo parabólico al ocular). Otro dato interesante de las hipérbolas es que para que un cometa ingrese al sistema solar, si la velocidad es lo suficientemente grande como para escapar del tirón gravitacional del Sol, entonces el camino que toma el cometa a medida que pasa por el sistema solar es hiperbólico.
Excentricidad y Directrix
Una forma alternativa de describir una sección cónica implica las directrices, los focos y una nueva propiedad llamada excentricidad. Veremos que el valor de la excentricidad de una sección cónica puede definir de manera única esa cónica.
La excentricidad \(e\)de una sección cónica se define como la distancia desde cualquier punto de la sección cónica hasta su foco, dividida por la distancia perpendicular desde ese punto hasta la directriz más cercana. Este valor es constante para cualquier sección cónica, y también puede definir la sección cónica:
- Si\(e=1\), la cónica es una parábola.
- Si\(e<1\), es una elipse.
- Si\(e>1,\) se trata de una hipérbola.
La excentricidad de un círculo es cero. La directriz de una sección cónica es la línea que, junto con el punto conocido como foco, sirve para definir una sección cónica. Las hipérbolas y elipses no circulares tienen dos focos y dos pautas asociadas. Las parábolas tienen un enfoque y una directrix.
Las tres secciones cónicas con sus pautas aparecen en la Figura\(\PageIndex{12}\).
Recordemos de la definición de una parábola que la distancia desde cualquier punto de la parábola al foco es igual a la distancia desde ese mismo punto a la directriz. Por lo tanto, por definición, la excentricidad de una parábola debe ser 1. Las ecuaciones de las pautas de una elipse horizontal son\(x=±\dfrac{a^2}{c}\). El vértice derecho de la elipse se encuentra en\((a,0)\) y el foco correcto está\((c,0)\). Por lo tanto la distancia desde el vértice al foco es\(a−c\) y la distancia desde el vértice a la directriz derecha es\(\dfrac{a^2}{c}−c.\) Esto da la excentricidad como
\[e=\dfrac{a−c}{\dfrac{a^2}{c}−a}=\dfrac{c(a−c)}{a^2−ac}=\dfrac{c(a−c)}{a(a−c)}=\dfrac{c}{a}. \nonumber \]
Ya que\(c<a\), este paso demuestra que la excentricidad de una elipse es menor que 1. Las pautas de una hipérbola horizontal también se localizan en\(x=±\dfrac{a^2}{c}\), y un cálculo similar muestra que la excentricidad de una hipérbola también es\(e=\dfrac{c}{a}\). Sin embargo en este caso tenemos\(c>a\), por lo que la excentricidad de una hipérbola es mayor a 1.
Determinar la excentricidad de la elipse descrita por la ecuación
\(\dfrac{(x−3)^2}{16}+\dfrac{(y+2)^2}{25}=1.\)
Solución
De la ecuación vemos que\(a=5\) y\(b=4\). El valor de c se puede calcular usando la ecuación\(a^2=b^2+c^2\) para una elipse. Sustituir los valores de a y b y resolver por c da\(c=3\). Por lo tanto, la excentricidad de la elipse es\(e=\dfrac{c}{a}=\dfrac{3}{5}=0.6.\)
Determinar la excentricidad de la hipérbola descrita por la ecuación
\(\dfrac{(y−3)^2}{49}−\dfrac{(x+2)^2}{25}=1.\)
- Pista
-
Primero encuentra los valores de a y b, luego determina c usando la ecuación\(c^2=a^2+b^2\).
- Contestar
-
\(e=\dfrac{c}{a}=\dfrac{\sqrt{74}}{7}≈1.229\)
Ecuaciones polares de secciones cónicas
A veces es útil escribir o identificar la ecuación de una sección cónica en forma polar. Para ello, necesitamos el concepto del parámetro focal. El parámetro focal de una sección cónica p se define como la distancia desde un foco hasta la directrix más cercana. La siguiente tabla da los parámetros focales para los diferentes tipos de cónicas, donde a es la longitud del semieje mayor (es decir, la mitad de la longitud del eje mayor), c es la distancia desde el origen al foco, y e es la excentricidad. En el caso de una parábola, a representa la distancia desde el vértice hasta el foco.
| Cónico | \(e\) | \(p\) |
|---|---|---|
| Elipse | \ (e\)” style="vertical-align:middle; ">\(0<e<1\) | \ (p\)” style="vertical-align:middle; ">\(\dfrac{a^2−c^2}{c}=\dfrac{a(1−e^2)}{c}\) |
| Parábola | \ (e\)” style="vertical-align:middle; ">\(e=1\) | \ (p\)” style="vertical-align:middle; ">\(2a\) |
| Hipérbola | \ (e\)” style="vertical-align:middle; ">\(e>1\) | \ (p\)” style="vertical-align:middle; ">\(\dfrac{c^2−a^2}{c}=\dfrac{a(e^2−1)}{c}\) |
Usando las definiciones del parámetro focal y la excentricidad de la sección cónica, podemos derivar una ecuación para cualquier sección cónica en coordenadas polares. En particular, suponemos que uno de los focos de una determinada sección cónica se encuentra en el polo. Entonces usando la definición de las diversas secciones cónicas en términos de distancias, es posible probar el siguiente teorema.
La ecuación polar de una sección cónica con parámetro focal p viene dada por
\(r=\dfrac{ep}{1±e\cos θ}\)o\(r=\dfrac{ep}{1±e\sin θ}.\)
En la ecuación de la izquierda, el eje mayor de la sección cónica es horizontal, y en la ecuación de la derecha, el eje mayor es vertical. Para trabajar con una sección cónica escrita en forma polar, primero haga que el término constante en el denominador sea igual a 1. Esto se puede hacer dividiendo tanto el numerador como el denominador de la fracción por la constante que aparece frente al más o menos en el denominador. Entonces el coeficiente del seno o coseno en el denominador es la excentricidad. Este valor identifica la cónica. Si el coseno aparece en el denominador, entonces la cónica es horizontal. Si aparece seno, entonces la cónica es vertical. Si ambos aparecen entonces los ejes se rotan. El centro de la cónica no está necesariamente en el origen. El centro está en el origen solo si la cónica es un círculo (i.e.,\(e=0\)).
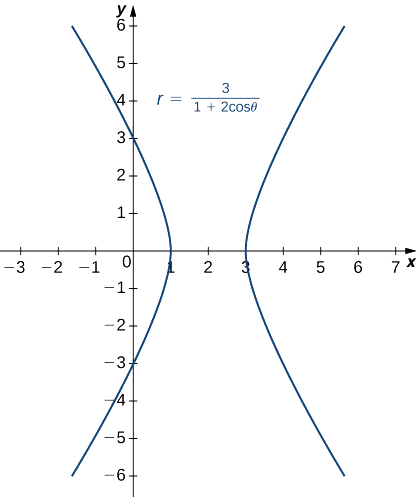
Identificar y crear una gráfica de la sección cónica descrita por la ecuación
\(r=\dfrac{3}{1+2\cos θ}\).
Solución
El término constante en el denominador es 1, por lo que la excentricidad de la cónica es 2. Esto es una hipérbola. El parámetro focal p se puede calcular utilizando la ecuación\(ep=3.\) Since\(e=2\), esto da\(p=\dfrac{3}{2}\). La función coseno aparece en el denominador, por lo que la hipérbola es horizontal. Elija algunos valores\(θ\) y cree una tabla de valores. Entonces podemos graficar la hipérbola (Figura\(\PageIndex{13}\)).
| \(θ\) | \(r\) | \(θ\) | \(r\) |
|---|---|---|---|
| \ (θ\)” style="vertical-align:middle; ">0 | \ (r\)” style="vertical-align:middle; ">1 | \ (θ\)” style="vertical-align:middle; ">\(π\) | \ (r\)” style="vertical-align:middle; ">−3 |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{π}{4}\) | \ (r\)” style="vertical-align:middle; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{5π}{4}\) | \ (r\)” style="vertical-align:middle; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{π}{2}\) | \ (r\)” style="vertical-align:middle; ">3 | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{3π}{2}\) | \ (r\)” style="vertical-align:middle; ">3 |
| \ (θ\)” style="vertical-align:middle; ">\(\dfrac{3π}{4}\) | \ (r\)” style="vertical-align:middle; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) | \ (θ\)” style="vertical-align:middle; ">\(\dfrac{7π}{4}\) | \ (r\)” style="vertical-align:middle; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) |
Identificar y crear una gráfica de la sección cónica descrita por la ecuación
\(r=\dfrac{4}{1−0.8 \sin θ}\).
- Pista
-
Primero encuentra los valores de e y p, y luego crea una tabla de valores.
- Contestar
-
Aquí\(e=0.8\) y\(p=5\). Esta sección cónica es una elipse.
Ecuaciones Generales de Grado Dos
Una ecuación general de grado dos se puede escribir en la forma
\[ Ax^2+Bxy+Cy^2+Dx+Ey+F=0. \nonumber \]
La gráfica de una ecuación de esta forma es una sección cónica. Si\(B≠0\) entonces se rotan los ejes de coordenadas. Para identificar la sección cónica, utilizamos el discriminante de la sección cónica\(4AC−B^2.\)
Uno de los siguientes casos debe ser cierto:
- \(4AC−B^2>0\). Si es así, la gráfica es una elipse.
- \(4AC−B^2=0\). Si es así, la gráfica es una parábola.
- \(4AC−B^2<0\). Si es así, la gráfica es una hipérbola.
El ejemplo más simple de una ecuación de segundo grado que involucra un término cruzado es\(xy=1\). Esta ecuación se puede resolver\(y\) para obtener\(y=\dfrac{1}{x}\). La gráfica de esta función se denomina hipérbola rectangular como se muestra.
Las asíntotas de esta hipérbola son los ejes\(x\) y\(y\) coordinados. Para determinar el ángulo θ de rotación de la sección cónica, utilizamos la fórmula\(\cot 2θ=\frac{A−C}{B}\). En este caso\(A=C=0\) y\(B=1\), así\(\cot 2θ=(0−0)/1=0\) y\(θ=45°\). El método para graficar una sección cónica con ejes girados implica determinar los coeficientes de la cónica en el sistema de coordenadas giradas. Los nuevos coeficientes están etiquetados\(A′,B′,C′,D′,E′,\) y\(F′,\) y están dados por las fórmulas
\[ \begin{align} A′ =A\cos^ 2θ+B\cos θ\sin θ+C\sin^2 θ \\ B′ =0 \\ C′ =A\sin^2 θ−B\sin θ\cos θ+C\cos^2θ \\ D′ =D\cos θ+E\sin θ \\ E′ =−D\sin θ+E\cosθ \\ F′ =F. \end{align} \nonumber \]
El procedimiento para graficar una cónica rotada es el siguiente:
- Identificar la sección cónica utilizando el discriminante\(4AC−B^2\).
- Determinar\(θ\) usando la fórmula\[\cot2θ=\dfrac{A−C}{B} \label{rot}. \]
- Calcular\(A′,B′,C′,D′,E′\), y\(F′\).
- Reescribir la ecuación original usando\(A′,B′,C′,D′,E′\), y\(F′\).
- Dibuja una gráfica usando la ecuación girada.
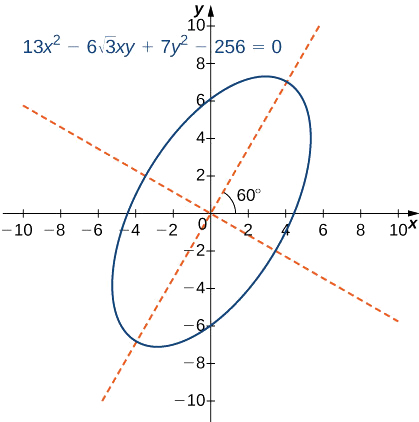
Identificar la cónica y calcular el ángulo de rotación de los ejes para la curva descrita por la ecuación
\[13x^2−6\sqrt{3}xy+7y^2−256=0. \nonumber \]
Solución
En esta ecuación,\(A=13,B=−6\sqrt{3},C=7,D=0,E=0,\) y\(F=−256\). El discriminante de esta ecuación es
\[4AC−B^2=4(13)(7)−(−6\sqrt{3})^2=364−108=256. \nonumber \]
Por lo tanto esta cónica es una elipse.
Para calcular el ángulo de rotación de los ejes, use Ecuación\ ref {rot}
\[\cot 2θ=\dfrac{A−C}{B}. \nonumber \]
Esto da
\(\cot 2θ=\dfrac{A−C}{B}=\dfrac{13−7}{−6\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\).
Por lo tanto\(2θ=120^o\) y\(θ=60^o\), que es el ángulo de rotación de los ejes.
Para determinar los coeficientes rotados, utilice las fórmulas dadas anteriormente:
\(A′=A\cos^2θ+B\cos θ\sinθ+C\sin^2θ\)
\(=13\cos^260+(−6\sqrt{3})\cos 60 \sin 60+7\sin^260\)
\(=13(\dfrac{1}{2})^2−6\sqrt{3}(\dfrac{1}{2})(\dfrac{\sqrt{3}}{2})+7(\dfrac{\sqrt{3}}{2})^2\)
\(=4,\)
\(B′=0\)
\(C′=A\sin^2θ−B\sin θ\cos θ+C\cos^2θ\)
\(=13\sin^260+(6\sqrt{3})\sin 60 \cos 60+7\cos^260\)
\(=13(\dfrac{\sqrt{3}}{2})^2+6\sqrt{3}(\dfrac{\sqrt{3}}{2})(\dfrac{1}{2})+7(\dfrac{1}{2})^2\)
\(=16,\)
\(D′=D\cos θ+E\sin θ\)
\(=(0)\cos 60+(0)\sin 60\)
\(=0,\)
\(E′=−D\sin θ+E\cos θ\)
\(=−(0)\sin 60+(0)\cos 60\)
\(=0\)
\(F′= F\)
\(=−256.\)
La ecuación de la cónica en el sistema de coordenadas giradas se convierte en
\(4(x′)^2+16(y′)^2=256\)
\(\dfrac{(x′)^2}{64}+\dfrac{(y′)^2}{16}=1\).
Una gráfica de esta sección cónica aparece de la siguiente manera.
Identificar la cónica y calcular el ángulo de rotación de los ejes para la curva descrita por la ecuación
\[3x^2+5xy−2y^2−125=0. \nonumber \]
- Pista
-
Siga los pasos 1 y 2 del método de cinco pasos descrito anteriormente
- Contestar
-
La cónica es una hipérbola y el ángulo de rotación de los ejes es\(θ=22.5°.\)
Conceptos clave
- La ecuación de una parábola vertical en forma estándar con enfoque y directriz dados es\(y=\dfrac{1}{4p}(x−h)^2+k\) donde\(p\) está la distancia desde el vértice al foco y\((h,k)\) son las coordenadas del vértice.
- La ecuación de una elipse horizontal en forma estándar es\(\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1\) donde el centro tiene coordenadas\((h,k)\), el eje mayor tiene longitud 2a, el eje menor tiene longitud 2b, y las coordenadas de los focos son\((h±c,k)\), donde\(c^2=a^2−b^2\).
- La ecuación de una hipérbola horizontal en forma estándar es\(\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1\) donde el centro tiene coordenadas\((h,k)\), los vértices están ubicados y las coordenadas de los focos son\((h±c,k),\) dónde\(c^2=a^2+b^2\).\((h±a,k)\)
- La excentricidad de una elipse es menor que 1, la excentricidad de una parábola es igual a 1, y la excentricidad de una hipérbola es mayor que 1. La excentricidad de un círculo es 0.
- La ecuación polar de una sección cónica con excentricidad e es\(r=\dfrac{ep}{1±ecosθ}\) o\(r=\dfrac{ep}{1±esinθ}\), donde p representa el parámetro focal.
- Para identificar una cónica generada por la ecuación\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\), primero calcule el discriminante\(D=4AC−B^2\). Si\(D>0\) entonces la cónica es una elipse, si\(D=0\) entonces la cónica es una parábola, y si\(D<0\) entonces la cónica es una hipérbola.
Glosario
- sección cónica
- una sección cónica es cualquier curva formada por la intersección de un plano con un cono de dos nappes
- directrix
- una directriz (plural: pautas) es una línea utilizada para construir y definir una sección cónica; una parábola tiene una directriz; elipses e hipérbolas tienen dos
- discriminante
- el valor\(4AC−B^2\), que se utiliza para identificar una cónica cuando la ecuación contiene un término que implica\(xy\), se llama discriminante
- enfoque
- un foco (plural: focos) es un punto utilizado para construir y definir una sección cónica; una parábola tiene un foco; una elipse y una hipérbola tienen dos
- excentricidad
- la excentricidad se define como la distancia desde cualquier punto de la sección cónica hasta su foco dividida por la distancia perpendicular desde ese punto hasta la directriz más cercana
- parámetro focal
- el parámetro focal es la distancia desde un foco de una sección cónica hasta la directrix más cercana
- forma general
- una ecuación de una sección cónica escrita como una ecuación general de segundo grado
- eje mayor
- el eje mayor de una sección cónica pasa por el vértice en el caso de una parábola o a través de los dos vértices en el caso de una elipse o hipérbola; también es un eje de simetría de la cónica; también llamado eje transversal
- eje menor
- el eje menor es perpendicular al eje mayor e interseca el eje mayor en el centro de la cónica, o en el vértice en el caso de la parábola; también llamado eje conjugado
- nappe
- una nappe es la mitad de un cono doble
- forma estándar
- una ecuación de una sección cónica que muestra sus propiedades, como la ubicación del vértice o longitudes de los ejes mayor y menor
- vértice
- un vértice es un punto extremo en una sección cónica; una parábola tiene un vértice en su punto de inflexión. Una elipse tiene dos vértices, uno en cada extremo del eje mayor; una hipérbola tiene dos vértices, uno en el punto de inflexión de cada rama


