5.4.2: Campo sobre el eje de un anillo

Última actualización
Guardar como PDF

Page ID: 131449

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Antes de comenzar, se puede obtener una idea cualitativa de cómo varía el campo en el eje de un anillo con la distancia desde el centro del anillo. Así, el campo en el centro del anillo será cero, por simetría. También será cero a una distancia infinita a lo largo del eje. En otros lugares no será cero; es decir, el campo primero aumentará, luego disminuirá, a medida que nos movemos a lo largo del eje. Habrá cierta distancia a lo largo del eje en el que el campo sea mayor. Vamos a querer saber dónde está esto, y cuál es su valor máximo.

\(\text{FIGURE V.1}\)
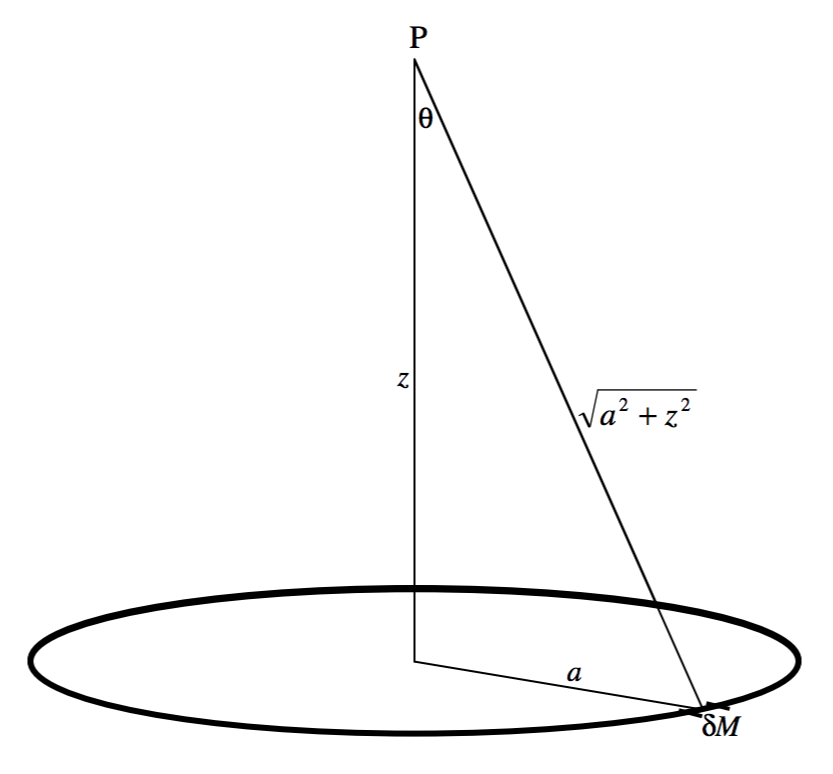
Figura 5.1.png

La Figura V.1 muestra un anillo de masa\(M\), radio\(a\). El problema es calcular la fuerza del campo gravitacional en\(\text{P}\). Comenzamos por considerar un pequeño elemento del anillo de masa\(δM\). La contribución de este elemento al campo es

\[\frac{GδM}{a^2+z^2}, \]

dirigido desde\(\text{P}\) hacia\(δM\). Esto se puede resolver en un componente a lo largo del eje (dirigido al centro del anillo) y un componente en ángulo recto con este. Cuando se agregan las contribuciones a todos los elementos alrededor de la circunferencia del anillo, este último componente será, por simetría, cero. El componente a lo largo del eje del anillo es

\[\frac{GδM}{a^2+z^2} \cos θ = \frac{GδM}{a^2+z^2} \cdot \frac{z}{\sqrt{a^2 + z^2}} = \frac{GδM z}{\left( a^2 + z^2 \right)^{3/2}}. \]

Al sumar las contribuciones de todos los elementos alrededor de la circunferencia del anillo, encontramos, para el campo gravitacional en\(\text{P}\)

\[g = \frac{GMz}{\left( a^2 + z^2 \right)^{3/2}} \label{5.4.4} \tag{5.4.4}\]

dirigido hacia el centro del anillo. Esto tiene la propiedad, como era de esperar, de ser cero en el centro del anillo y a una distancia infinita a lo largo del eje. Si expresamos\(z\) en unidades de\(a\), y\(g\) en unidades de\(GM/a^2\), esto se convierte en

\[g = \frac{z}{\left( 1 + z^2 \right)^{3/2}}. \label{5.4.5} \tag{5.4.5}\]

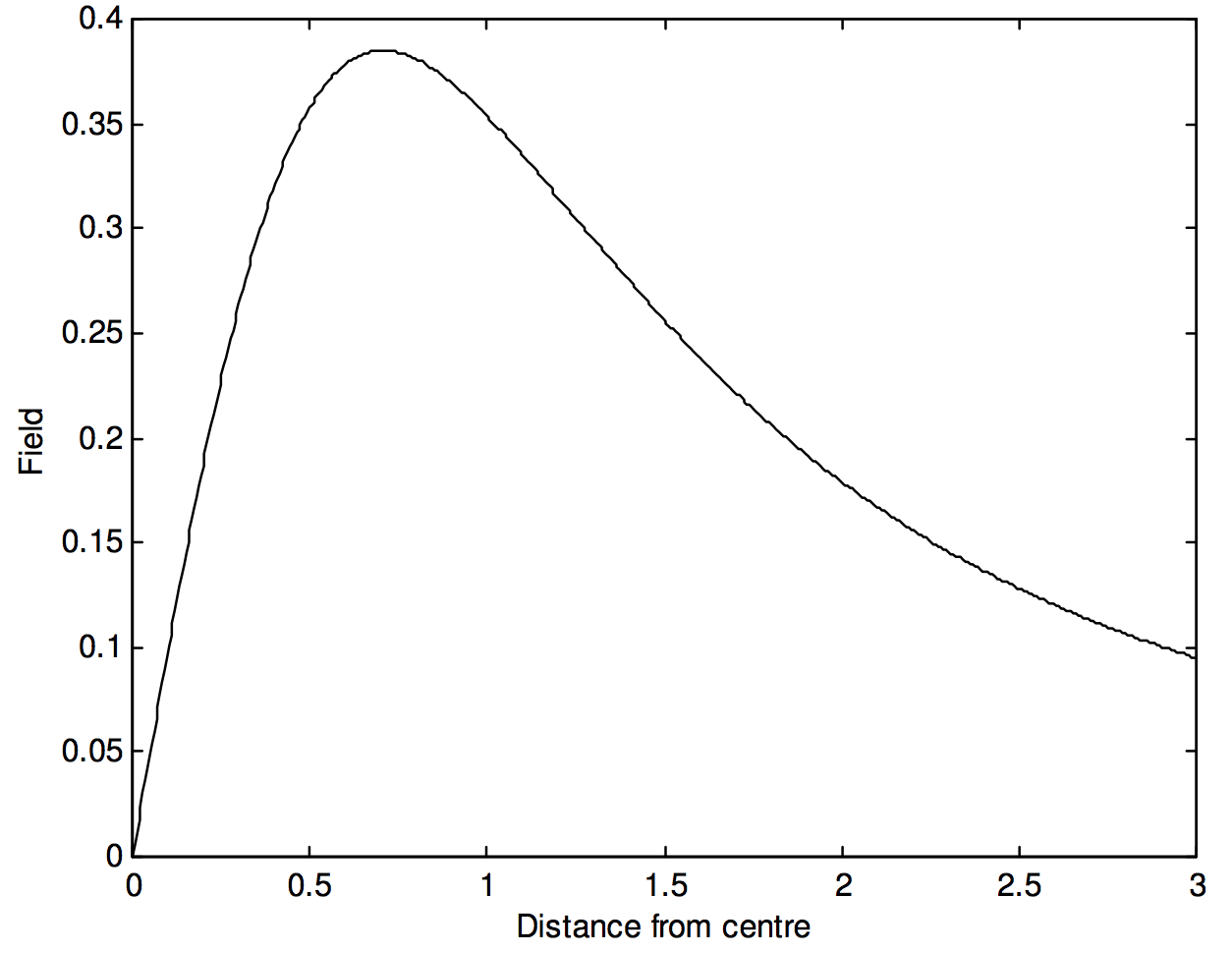
Esto se ilustra en la figura V.2.

Excercise: Demostrar que el campo alcanza su mayor valor de\(\frac{\sqrt{12} GM}{9a^2} = \frac{0.385 GM}{a^2}\) dónde\(z = a/√2 = 0.707a\). Demostrar que el campo tiene la mitad de este valor máximo donde\(z = 0.2047a\) y\(z = 1.896a\).

\(\text{FIGURE V.2}\)
Figura 5.2.png