5.4.3: Discos planos

\(\text{FIGURE V.2A}\)

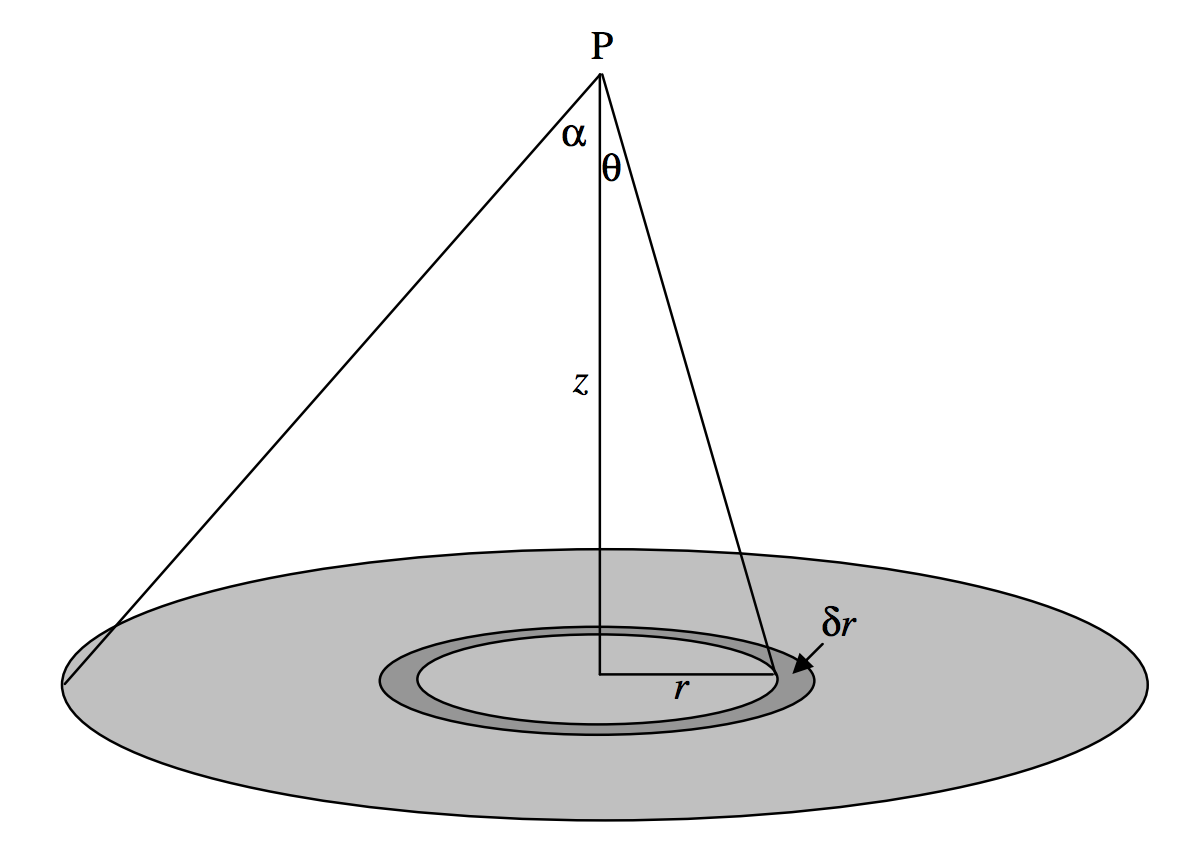
Considere un disco de densidad superficial (masa por unidad de área)\(σ\)\(a\), radio y un punto\(\text{P}\) en su eje a una\(z\) distancia del disco. La contribución al campo a partir de un anillo elemental, radios\(r\)\(r + δr\), masa\(2πσ \ r \ δr\) es (de la Ecuación 5.4.1)

\[δg = 2 \pi G σ \frac{zrδr}{\left( z^2 + r^2 \right)^{3/2}}. \label{5.4.6} \tag{5.4.6}\]

Para encontrar el campo de todo el disco, simplemente integre de\(r = 0\) a\(a\), y, si el disco es de densidad superficial uniforme,\(σ\) estará fuera de la señal integral. Será más fácil integrarse con respecto a\(θ\) (de\(0\) a\(α\)), dónde\(r = z \tan θ\). Deberías obtener

\[g = 2 \pi G σ (1 - \cos α), \label{5.4.7} \tag{5.4.7}\]

o, con\(M = \pi a^2 σ\),

\[g = \frac{2GM (1-\cos α)}{a^2}. \label{5.4.8} \tag{5.4.8}\]

Ahora\(2\pi (1 − \cos α)\) es el ángulo sólido\(ω\) subtendido por el disco en\(\text{P}\). (Convénzase de esto — no se limite a tomar mi palabra para ello.) Por lo tanto

\[g = G σ ω . \label{5.4.9} \tag{5.4.9}\]

Esta expresión también es la misma para una lámina plana uniforme de cualquier forma, para la componente descendente del campo gravitacional. Para, considere la figura\(\text{V.3}\).

El componente descendente del campo debido al elemento\(δ\text{A}\) es\(\frac{Gσδ A \cos θ}{r^2} = G σ δω\). Así, si te integras sobre toda la lámina, llegas a\(Gσω\).

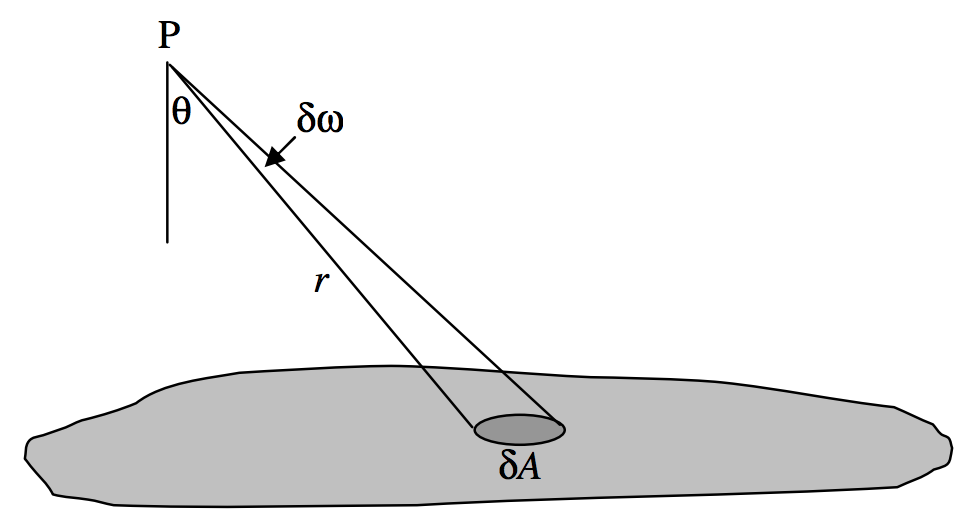
\(\text{FIGURE 5.3}\)

Volviendo a la Ecuación\(\ref{5.4.8}\), podemos escribir la Ecuación en términos de\(z\) más que\(α\). Si expresamos\(g\) en unidades de\(GM/a^2\) y\(z\) en unidades de\(a\), la Ecuación se convierte

\[g = 2 \left( 1 - \frac{z}{\sqrt{1+z^2}} \right) . \label{5.4.10} \tag{5.4.10}\]

Esto se ilustra en la figura\(\text{V.4}\).

\(\text{FIGURE V.4}\)

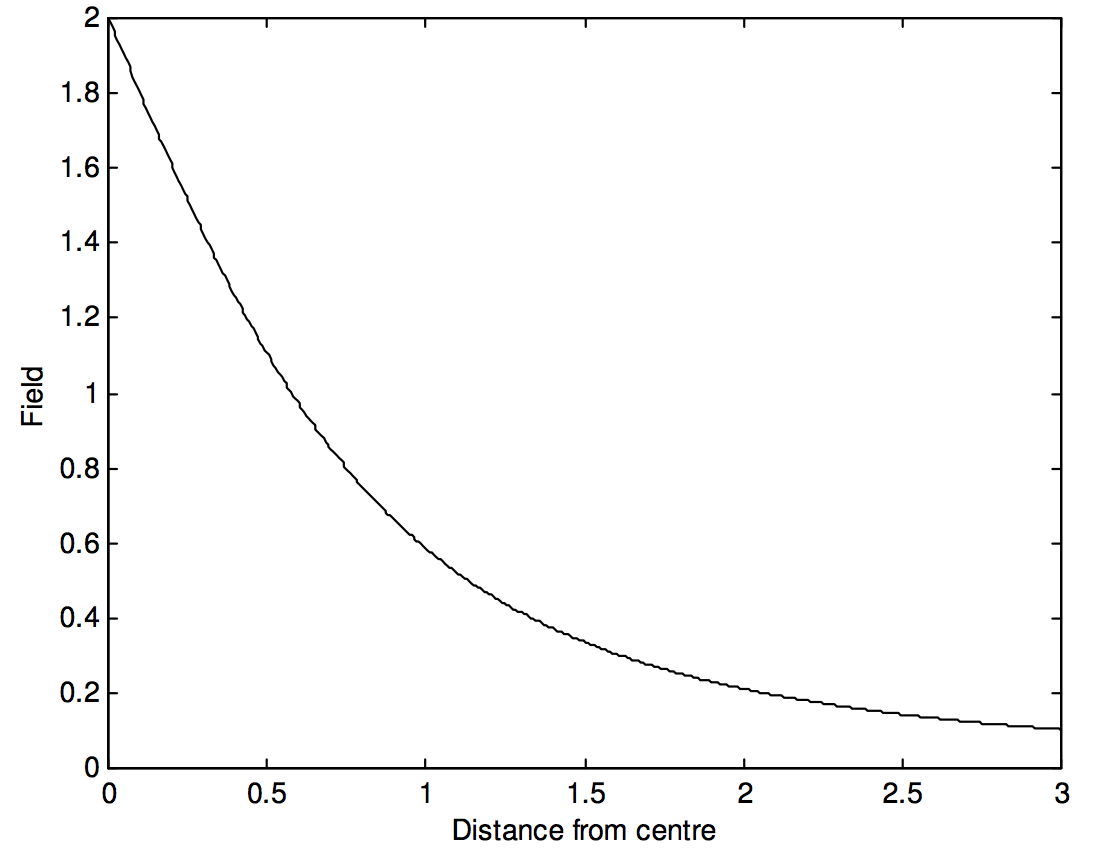
El campo es mayor inmediatamente por encima del disco. En el lado opuesto del disco, el campo cambia de dirección. En el plano del disco, en el centro del disco, el campo es cero. Para más información sobre esto, véase la Subsección 5.4.7.

Si estás calculando el campo sobre el eje de un disco que no es de densidad superficial uniforme, pero cuya densidad superficial varía como\(σ(r)\), tendrás que calcular

\[M = 2 \pi \int_0^a σ(r) r dr \label{5.4.11} \tag{5.4.11}\]

y\[g = 2 \pi G z \int_0^a \frac{σ (r) r dr}{\left( z^2 + r^2 \right)^{3/2}}. \label{5.4.12} \tag{5.4.12}\]

Podrías probar, por ejemplo, algunos de los siguientes formularios para\(σ(r)\):

\[σ_0 \left( 1 - \frac{kr}{a} \right), \quad σ_0 \left( 1 - \frac{kr^2}{a} \right), \quad σ_0 \sqrt{1-\frac{kr}{a}}, \quad σ_0 \sqrt{1- \frac{kr^2}{a^2}}. \]

Si te interesan las galaxias, quizás quieras probar modelar una galaxia como una protuberancia esférica central de densidad\(ρ\) y radio\(a_1\), más un disco de densidad superficial\(σ(r)\) y radio\(a_2\), y desde allí podrás trabajar tu camino hasta modelos más sofisticados.

En esta sección hemos calculado el campo sobre el eje de un disco. Tan pronto como te mueves fuera del eje, se vuelve mucho más difícil.

Ejercicio. Partiendo de las Ecuaciones 5.4.1 y\(\ref{5.4.10}\), muestran que a variar grandes distancias a lo largo del eje, los campos para un anillo y para un disco se vuelven cada uno\(GM/z^2\). Todo lo que tienes que hacer es expandir las expresiones binomialmente en\(a/z\). El campo a una gran distancia r de cualquier objeto finito se acercará\(GM/r^2\).