5.4.8: Cáscara Esférica Hueca

Última actualización
Guardar como PDF

Page ID: 131472

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Imaginamos una concha esférica hueca de radio\(a\)\(σ\), densidad superficial y un punto\(\text{P}\) a una\(r\) distancia del centro de la esfera. Considera una zona elemental de espesor\(δx\). La masa de este elemento es\(2πaσ \ δx\). (En caso de que lo dudes, o no lo sabías, “el área de una zona en la superficie de una esfera es igual al área correspondiente proyectada sobre el cilindro circunscrito”.)

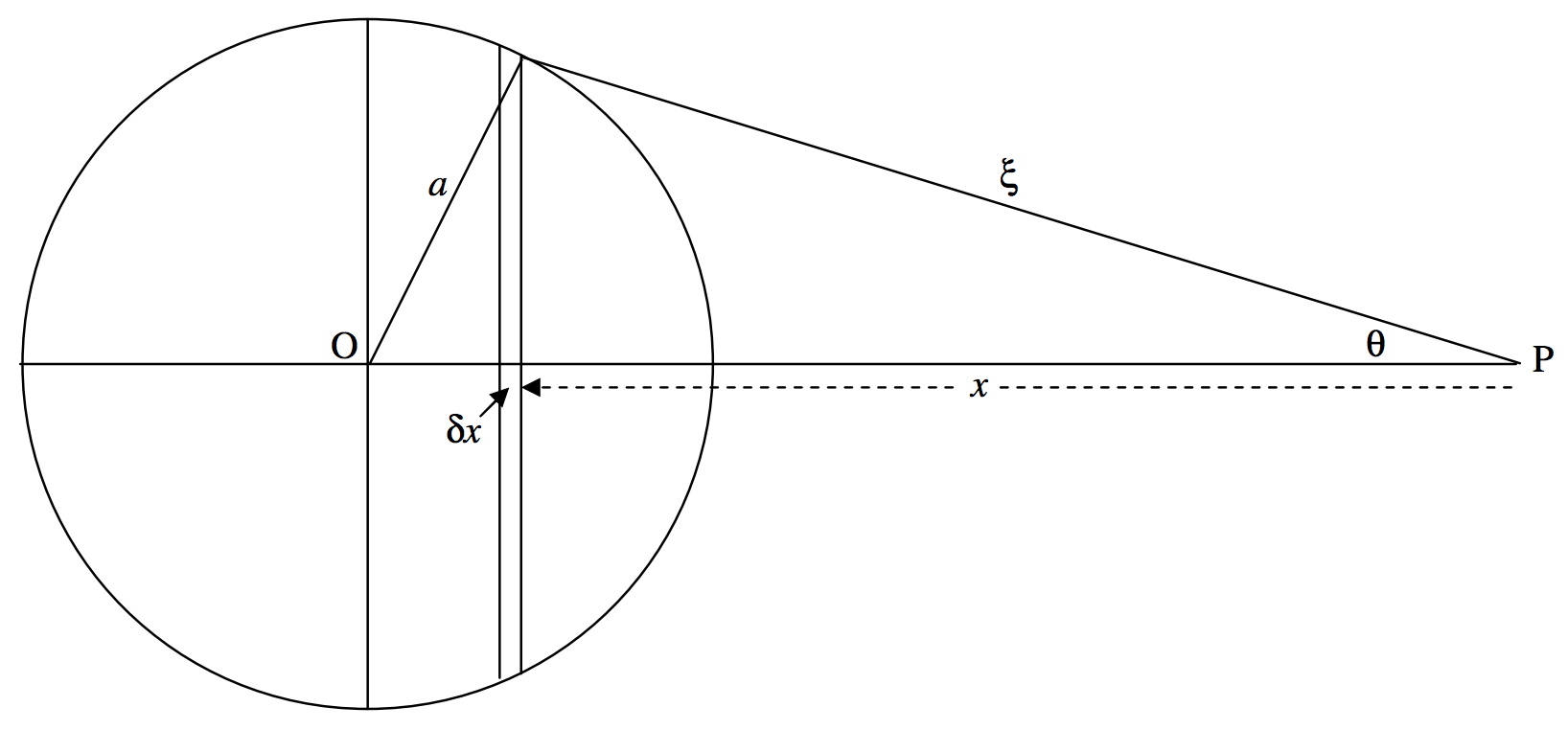
Figura 5.9.png
\(\text{FIGURE V.9}\)

El campo debido a esta zona, en la dirección\(\text{PO}\) es

\[\frac{2 πaσG \cos θδx}{ξ^2}.\]

Expresemos todo esto en términos de una sola variable,\(ξ\). Vamos a tener que expresarnos\(x\) y\(θ\) en términos de\(ξ\).

Tenemos

\[a^2 = r^2 + ξ^2 - 2rξ \cos θ = r^2 + ξ^2 - 2rx,\]

de la cual

\[\cos θ = \frac{r^2 - a^2 + ξ^2}{2rξ} \quad δx = \frac{ξδξ}{r}.\]

Por lo tanto el campo a\(\text{P}\) debido a la zona es\(\frac{\pi a G σ}{r^2} \left( 1 + \frac{r^2 - a^2}{ξ^2} \right) δξ\).

Si\(\text{P}\) es un punto externo, para poder encontrar el campo debido a toda la concha esférica, integramos de\(ξ = r − a\) a\(r + a\). Esto da como resultado

\[g = \frac{GM}{r^2} . \label{5.4.23}\]

Sin embargo, si\(\text{P}\) es un punto interno, con el fin de encontrar el campo debido a toda la concha esférica, integramos de\(ξ = a − r\) a\(a + r\), lo que resulta en\(g = 0\).

Así tenemos el resultado importante de que el campo en un punto externo debido a una concha esférica hueca es exactamente el mismo que si toda la masa estuviera concentrada en un punto en el centro de la esfera, mientras que el campo dentro de la esfera es cero.

Precaución. El campo dentro de la esfera es cero sólo si no hay otras masas presentes. La esfera hueca no te va a proteger del campo gravitacional de ninguna otra masa que pudiera estar presente. Así, en la figura V.10, el campo at\(\text{P}\) es la suma del campo debido a la esfera hueca (que de hecho es cero) y el campo de la masa\(M\), que no es cero. El anti-GRAV es un dispositivo útil en la ciencia ficción, pero no ocurre en los hechos científicos.

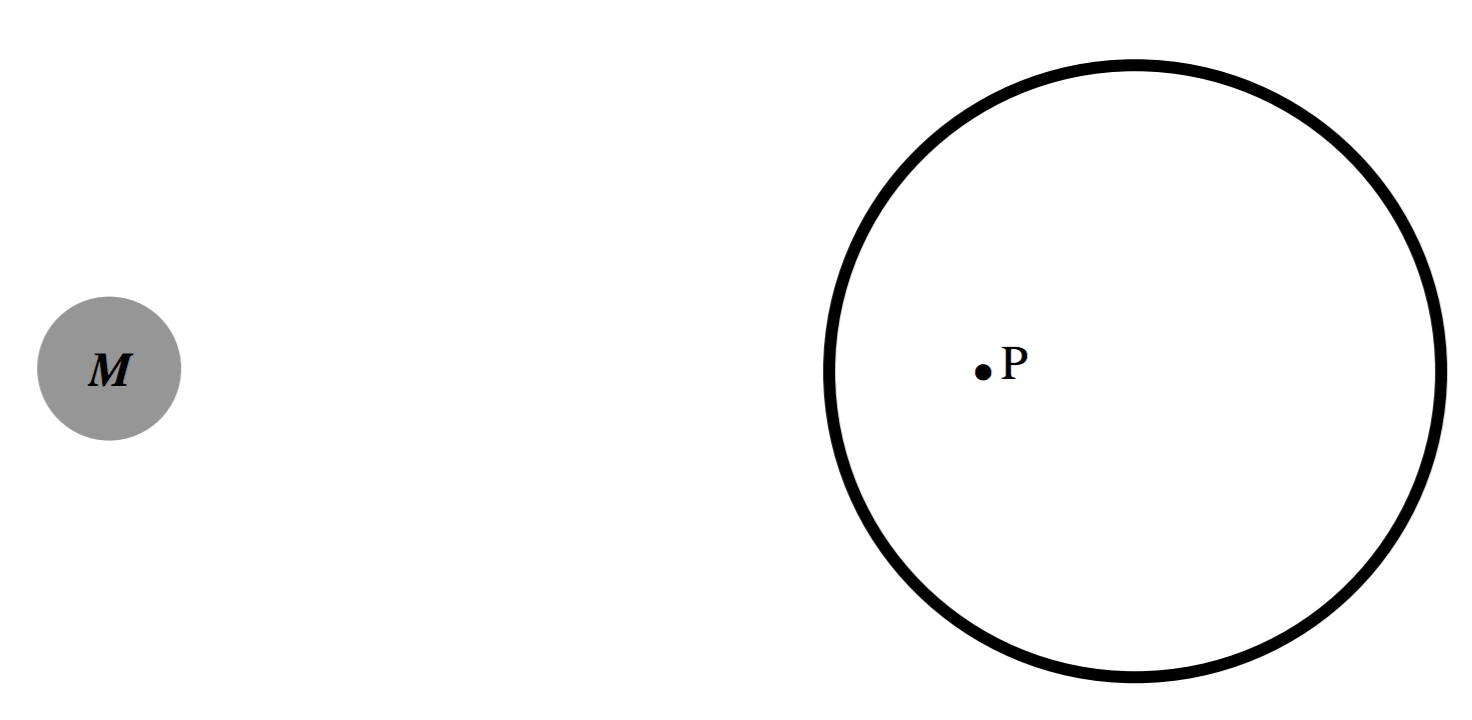
Figura 5.10.png
\(\text{FIGURE V.10}\)