5.5: Teorema de Gauss

Última actualización
Guardar como PDF

Page ID: 131334

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Gran parte de lo anterior puede haber sido una buena práctica de integración, pero ahora veremos que muchos de los resultados son inmediatamente obvios del Teorema de Gauss —en sí misma una ley trivialmente obvia. (O digamos que, como muchas cosas, es trivialmente obvio en retrospectiva, ¡aunque necesitaba que Carl Friedrich Gauss lo señalara!)

Primero definamos el flujo gravitacional\(Φ\) como una cantidad extensa, siendo producto del campo gravitacional y el área:

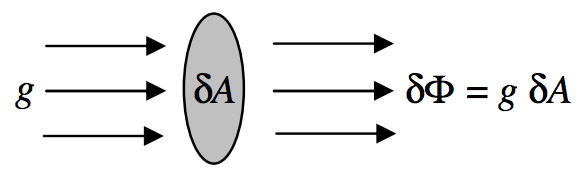
Figura 5.12.png
\(\text{FIGURE V.12}\)

Si\(\textbf{g}\) y no\(δ\textbf{A}\) son paralelos, el flujo es una cantidad escalar, siendo el producto escalar o punto de\(\textbf{g}\) y\(δ\textbf{A}\):

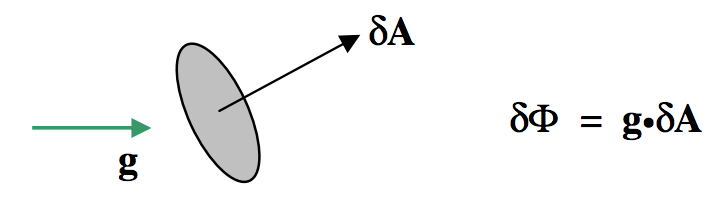
Figura 5.13.png
\(\text{FIGURE V.13}\)

Si el campo gravitacional está enhebrando a través de una gran área finita, tenemos que calcular\(\textbf{g}•δ\textbf{A}\) para cada elemento de área de la superficie, la magnitud y dirección de\(\textbf{g}\) posiblemente variar de punto a punto sobre la superficie, y luego tenemos que integrar esto en toda la superficie. Es decir, tenemos que calcular una integral de superficie. Daremos algunos ejemplos a medida que avancemos, pero primero pasemos hacia el teorema de Gauss.

En la figura\(\text{V.14}\), he dibujado una masa\(M\) y varias de las líneas de campo gravitacional que convergen sobre ella. También he dibujado una esfera de radio\(r\) alrededor de la masa. A una distancia\(r\) de la masa, el campo es\(GM/r^2\). La superficie de la esfera es\(4 \pi r^2\). Por lo tanto, el flujo interno total, producto de estos dos términos\(4 \pi GM\), es, y es independiente del tamaño de la esfera. (Es independiente del tamaño de la esfera porque el campo cae inversamente como el cuadrado de la distancia. Así, el teorema de Gauss es un teorema que se aplica a campos cuadrados inversos). Nada cambia si la masa no está en el centro de la esfera. Tampoco cambia si (figura\(\text{V.15}\)) la superficie no es una esfera. Si hubiera varias masas dentro de la superficie, cada una contribuiría\(4 \pi G\) multiplicada por su masa al flujo total normal hacia adentro. Así, el flujo interno normal total a través de cualquier superficie cerrada es igual a\(4 \pi G\) veces la masa total encerrada por la superficie. O, expresó de otra manera:

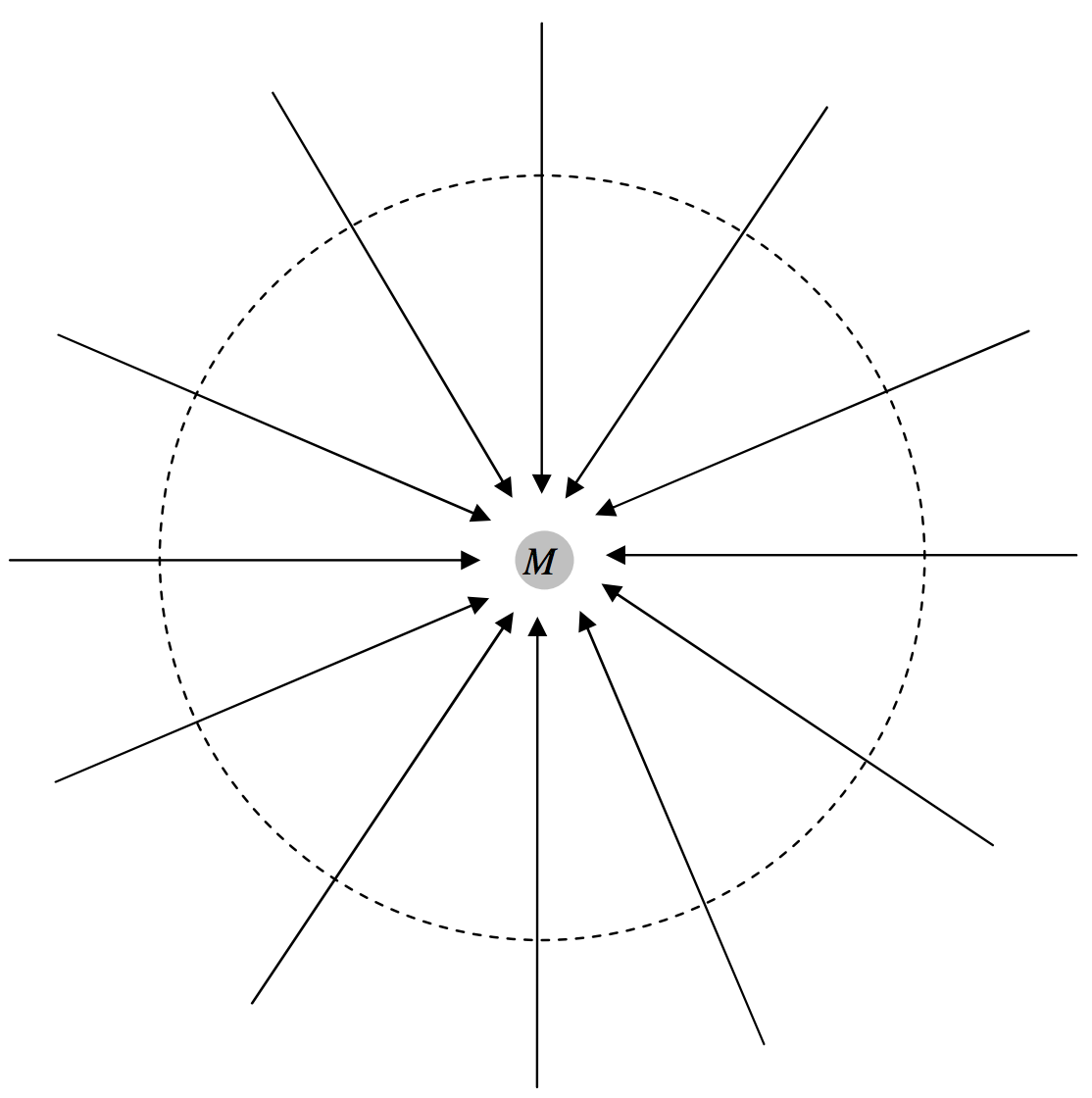
Figura 5.14.png
\(\text{FIGURE V.14}\)

El flujo gravitacional exterior normal total a través de una superficie cerrada es igual a\(−4 \pi G\) veces la masa total encerrada por la superficie.

Este es el teorema de Gauss.

Matemáticamente, el flujo a través de la superficie se expresa por la integral de la superficie\(∫∫\textbf{g}⋅d\textbf{A}\). Si existe una distribución continua de materia dentro de la superficie, de densidad\(ρ\) que varía de punto a punto y es función de las coordenadas, la masa total dentro de la superficie se expresa por\(∫∫∫ρdV\). Así, el teorema de Gauss se expresa matemáticamente por

\[∫∫ \textbf{g} \cdot d \textbf{A} = -4 \pi G ∫∫∫ ρ dV . \label{5.5.1} \tag{5.5.1}\]

Debe verificar las dimensiones de esta Ecuación.

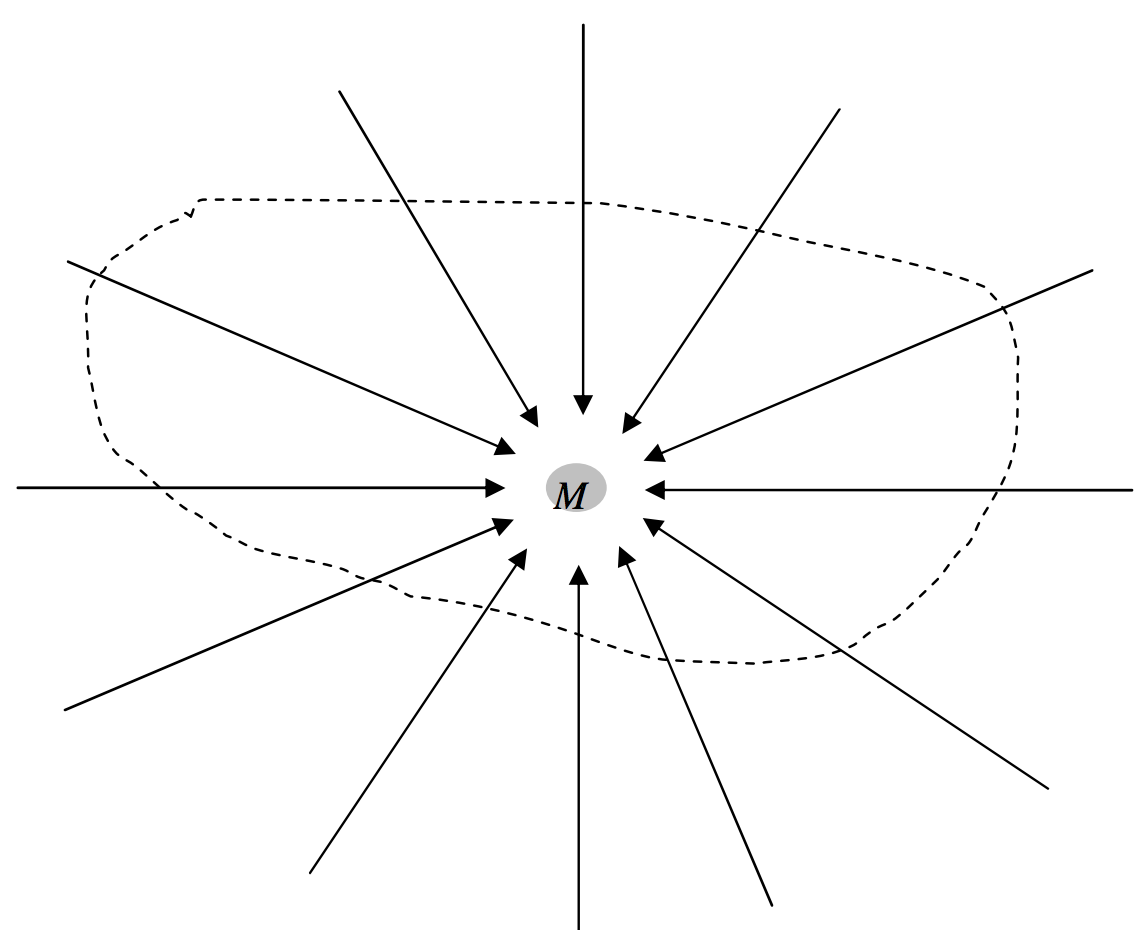
Figura 5.15.png
\(\text{FIGURE V.15}\)

En la figura\(\text{V.16}\) he dibujado superficies esféricas gaussianas de radio\(r\) exterior e interior de esferas huecas y sólidas. En\(a\) y\(c\), el flujo hacia afuera a través de la superficie es solo\(−4 \pi G\) multiplicado por la masa encerrada\(M\); el área superficial de la superficie gaussiana es\(4 \pi r^2\). Este es el campo exterior en la superficie gaussiana (es decir, a una\(r\) distancia del centro de la esfera\(−GM/r^2\). En\(b\), no hay masa dentro de la superficie gaussiana, y por lo tanto el campo es cero. En\(d\), la masa dentro de la superficie gaussiana es\(M_r\), y así lo es el campo exterior\(−GM_r /r^2\).

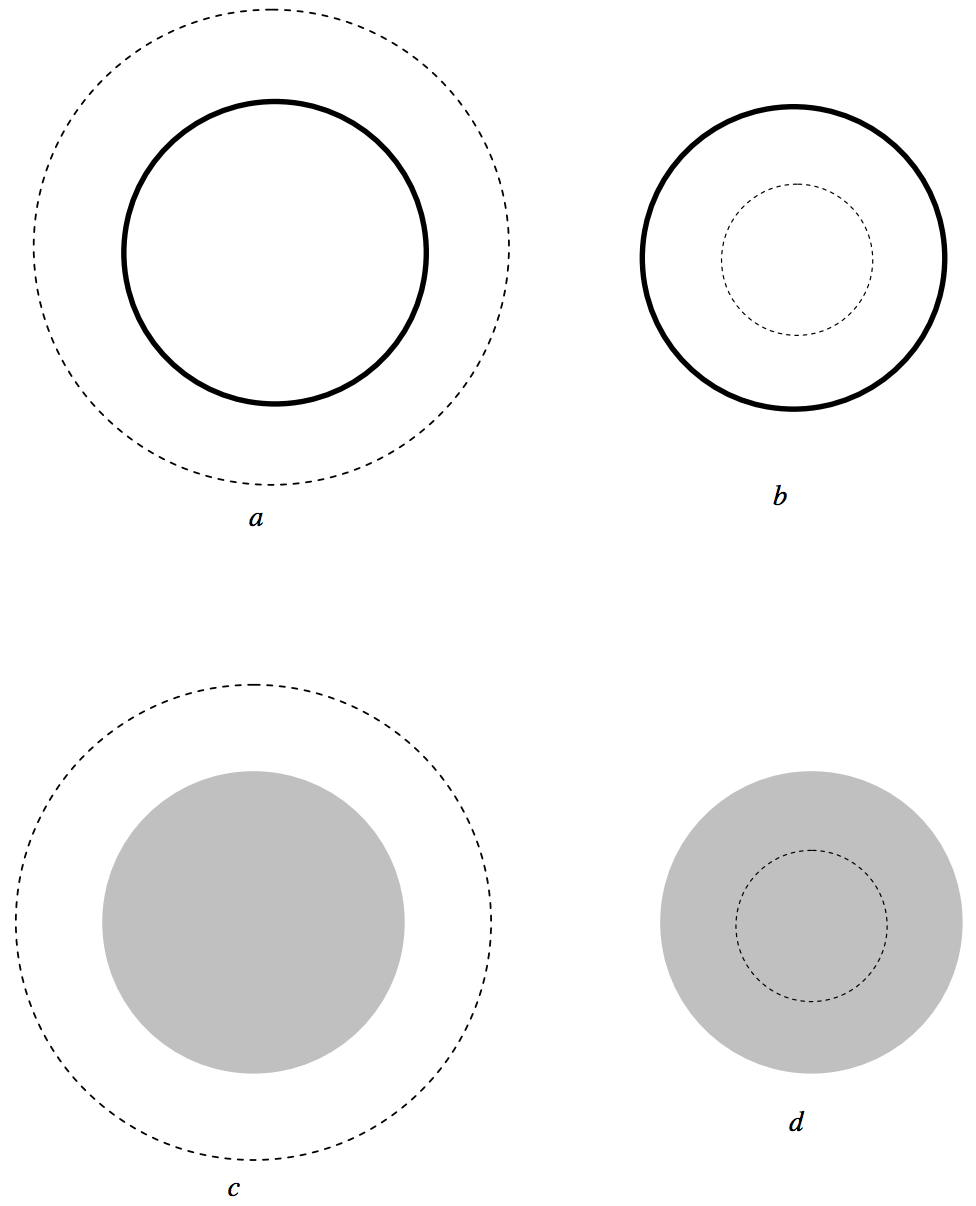
Figura 5.16.png
\(\text{FIGURE V.16}\)

En la figura\(\text{V.17}\) dibujo (parte de una) varilla infinita de masa\(λ\) por unidad de longitud, y una superficie gaussiana cilindircal de radio\(h\) y longitud\(l\) alrededor de ella.

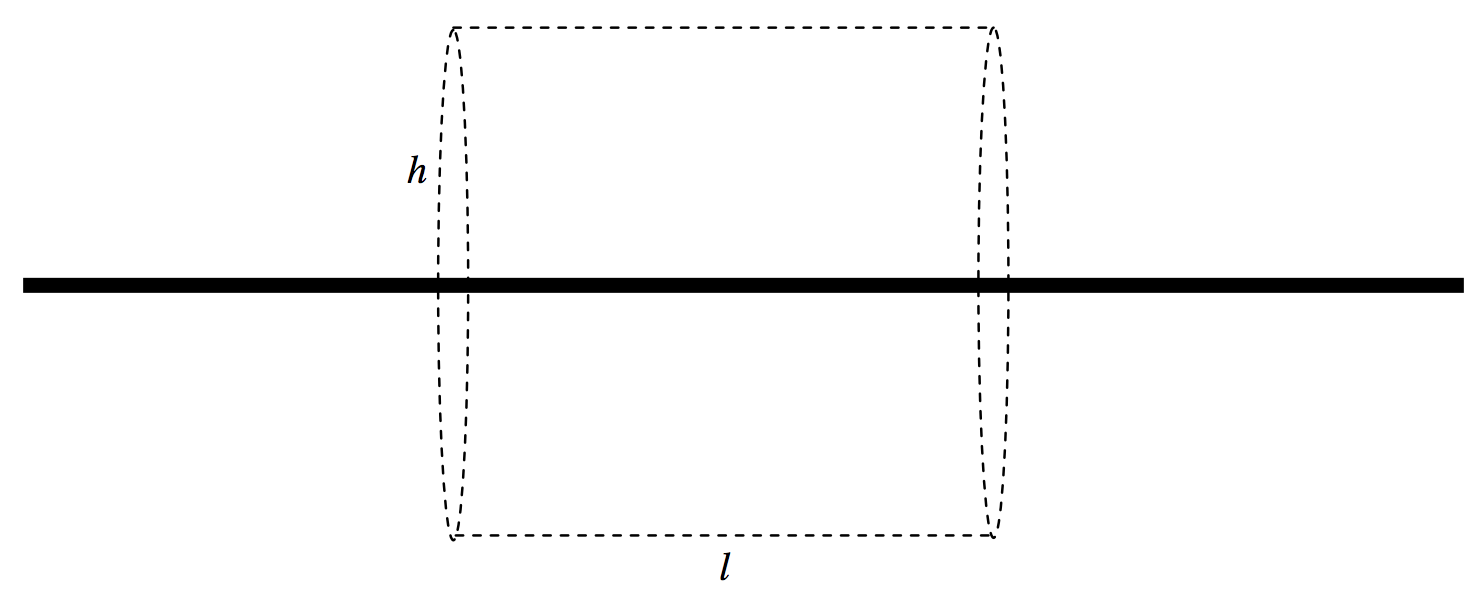
Figura 5.17.png
\(\text{FIGURE V.17}\)

El área de superficie de la superficie curva del cilindro es\(2 \pi hl\), y la masa encerrada dentro de él es\(λl\). Así, el campo exterior en la superficie del cilindro gaussiano (es decir, a una\(h\) distancia de la varilla) es\(−4 \pi G × λl ÷ 2 \pi hl = −2Gλ/h\), de acuerdo con la Ecuación 5.4.18.

En la figura\(\text{V.18}\) he dibujado (parte de) una lámina plana infinita de densidad superficial\(σ\), y una superficie gaussiana cilíndrica o área transversal\(A\) y altura\(2h\).

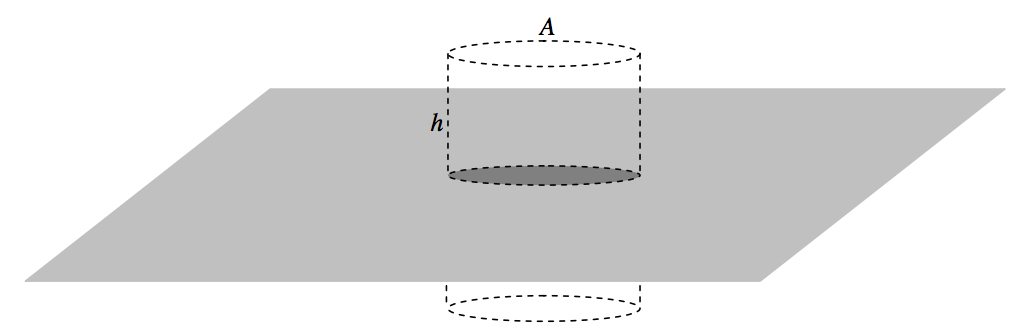
Figura 5.18.png
\(\text{FIGURE V.18}\)

La masa encerrada por el cilindro es\(σA\) y el área de los dos extremos del cilindro es\(2A\). El campo exterior en los extremos del cilindro (es decir, a una\(h\) distancia de la lámina plana) está\(−4\pi G × σA ÷ 2A = −2πGσ\), por lo tanto, de acuerdo con la Ecuación 5.4.13.