5.6: Cálculo de Integrales de Superficie

Si bien el concepto de una integral de superficie suena bastante fácil, ¿cómo calculamos realmente una en la práctica? En esta sección hago dos ejemplos.

Ejemplo\(\PageIndex{1}\)

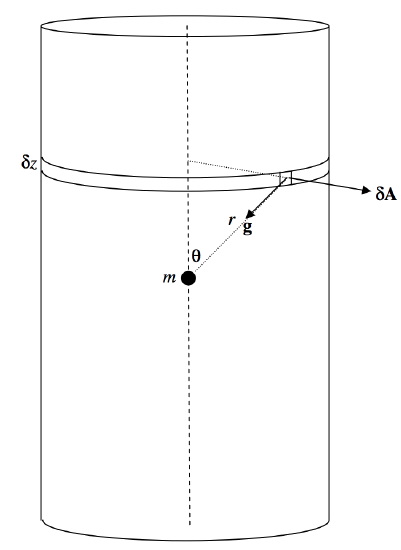
En la Figura\(\text{V.19}\) muestro una pequeña masa\(m\), y la he rodeado con un cilindro o radio\(a\) y altura\(2h\). El problema es calcular la superficie integral\(∫ \textbf{g} \cdot d\textbf{A}\) a través de toda la superficie del cilindro. Por supuesto que ya sabemos, por el teorema de Gauss\(= −4 \pi Gm\), que la respuesta es, pero nos gustaría ver una integral superficial realmente realizada.

\(\text{FIGURE V.19}\)

He dibujado un pequeño elemento de la superficie. Su área\(δA\) es\(dz\) tiempos\(aδ \phi\), donde\(\phi\) está el ángulo azimutal habitual de coordenadas cilíndricas. Es decir,\(δA = a \ δz \ δ\phi\). La magnitud\(g\) del campo que hay\(Gm/r^2\), y el ángulo entre\(\textbf{g}\) y\(d\textbf{A}\) es\(90^\circ + θ\). El flujo hacia afuera a través del elemento pequeño es

\[\textbf{g} \cdot δ \textbf{A} = \frac{Gma \cos (θ+90^\circ) δz δ \phi}{r^2}.\]

(Esto es negativo —es decir, en realidad es un flujo interno— porque\(\cos (θ + 90^\circ ) = −\sin θ\).) Cuando se integra alrededor de la tira elemental\(δz\), esto es\(- \frac{2 \pi Gma \sin θ δz}{r^2}.\) Para encontrar el flujo sobre la superficie curva total, integremos esto de\(z = 0\) a\(h\) y doblarlo, o, más fácil, de\(θ = \pi/2\) a\(α\) y doblarlo, donde\(\tan α = a/h\). Tendremos que expresarnos\(z\) y\(r\) en términos de\(θ\) (eso es fácil: -\(z = a \cot θ\) y\(r = a \csc θ\)), y la integral se vuelve

\[4 \pi Gm \int_{\pi/2}^α \sin θ \ d θ = -4 \pi Gm \cos α \label{5.6.1} \tag{5.6.1}\]

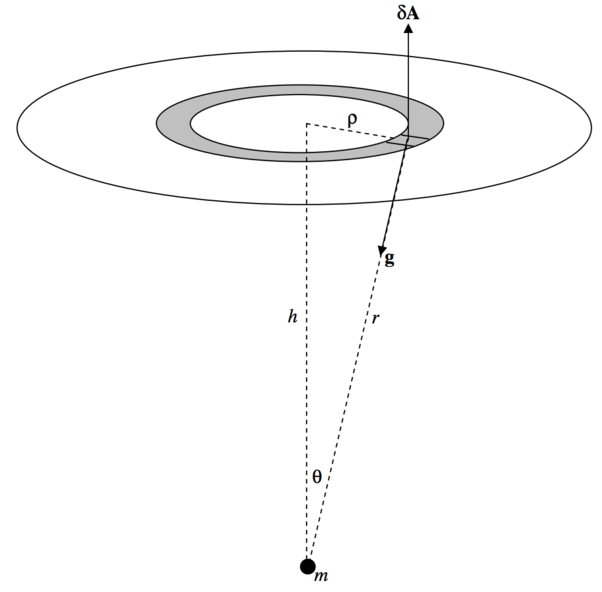
Ahora encontremos el flujo a través de uno de los extremos planos del cilindro.

\(\text{FIGURE V.20}\)

Esta vez,\(δA = ρ \ δρ \ δ\phi\),\(g = Gm/r^2\) y el ángulo entre\(\textbf{g}\) y\(δ\textbf{A}\) es\(180^\circ − θ\). El flujo hacia afuera a través del elemento pequeño es\(\frac{Gmρ \cos (180^\circ - θ)δρδ\phi}{r^2}\) y cuando se integra alrededor del anillo esto se vuelve\(-\frac{2\pi Gm \cos θ \ ρδρ}{r^2}\). Ahora tenemos que integrar esto de\(ρ = 0\) a\(a\), o, mejor, de\(θ = 0\) a\(α\). Tenemos\(r = h \sec θ\) y\(ρ = h \tan θ\), y la integral se convierte

\[-2 \pi Gm \int_0^α \sin θ d θ = - 2\pi Gm (1- \cos α). \label{5.6.2} \tag{5.6.2}\]

Hay dos extremos, por lo que el flujo total a través de todo el cilindro es el doble de esto más la ecuación\(\ref{5.6.1}\) para dar

\[\phi = -4\pi Gm, \label{5.6.3} \tag{5.6.3}\]

como se esperaba del teorema de Gauss.

Ejemplo\(\PageIndex{2}\)

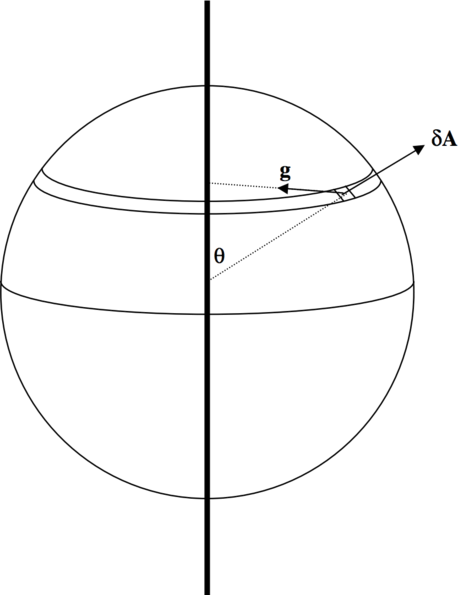
En la figura\(\text{V.21}\) he dibujado (parte de) una varilla infinita cuya masa por unidad de longitud es\(λ\). He dibujado a su alrededor una esfera de radio\(a\). El problema será determinar el flujo normal total a través de la esfera. Por el teorema de Gauss, sabemos que la respuesta debe ser\(−8πGαλ\).

\(\text{FIGURE V.21}\)

El vector\(δ\textbf{A}\) que representa el elemento de área se dirige lejos del centro de la esfera, y el vector\(\textbf{g}\) se dirige hacia el punto más cercano de la varilla. El ángulo entre ellos es\(θ + 90^\circ\). La magnitud de\(δ\textbf{A}\) en coordenadas esféricas es\(a^2 \sin θδθδ \phi\), y la magnitud de\(\textbf{g}\) es (ver Ecuación 5.4.15)\(\frac{2Gλ}{a \sin θ}.\) El producto punto\(\textbf{g}⋅δ \textbf{A}\) es

\[ \frac{2Gλ}{a \sin θ} \cdot a^2 \sin θδθδ \phi \cdot \cos ( θ + 90^\circ) = - 2 G λ a \sin θδθδ \phi . \label{5.6.4} \tag{5.6.4}\]

Para encontrar el flujo total, este debe integrarse desde\(\phi = 0\) hacia\(2 \pi \) y desde\(θ = 0\) hasta\(\pi\). El resultado, como se esperaba, es\(−8 \pi Gαλ\).