5.8.6: Varillas

Última actualización
Guardar como PDF

Page ID: 131349

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Consulte la figura\(\text{V.5}\). El potencial a\(\text{P}\) debido al elemento\(δx\) es\(-\frac{Gλδx}{r} = − Gλ \sec θδθ\). El potencial total en\(\text{P}\) es por lo tanto

\[ψ = - G λ \int_α^β \sec θdθ = - Gλ \ln \left[ \frac{\sec β + \tan β}{\sec α + \tan α} \right] . \label{5.8.15} \tag{5.8.15}\]

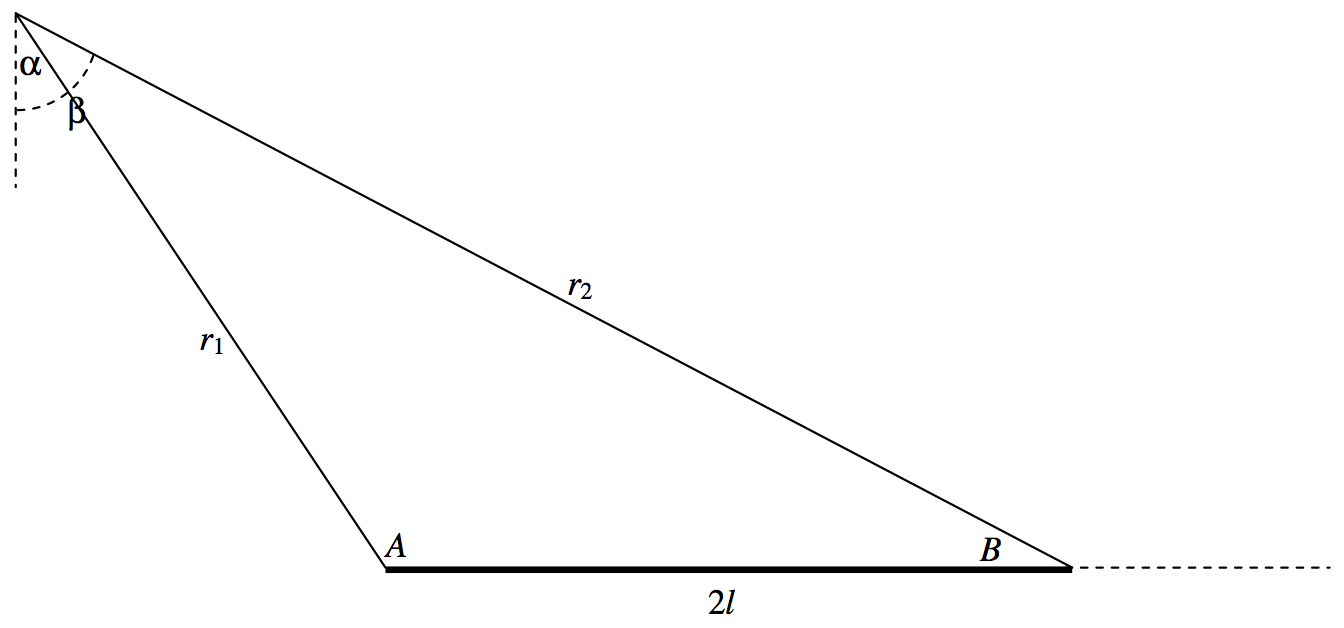
Figura 5.24.png
\(\text{FIGURE V.24}\)

Refiérase ahora a la figura\(\text{V.24}\), en la que\(A = 90^\circ + α\) y\(B = 90^\circ − β\).

\[\frac{\sec β + \tan β}{\sec α + \tan α} = \frac{\cos α (1+ \sin β)}{\cos β (1 + \sin α)} = \frac{\sin A (1+ \cos B)}{\sin B(1-\cos A)} = \frac{2 \sin \frac{1}{2}A \cos \frac{1}{2} A . 2 \cos^2 \frac{1}{2} B}{2\sin \frac{1}{2} B \cos \frac{1}{2} B . 2 \sin^2 \frac{1}{2} A} = \cot \frac{1}{2} A \cot \frac{1}{2} B = \sqrt{\frac{s(s-r_2)}{(s-r_1)(s-2l)}}\cdot \sqrt{\frac{s(s-r_1)}{(s-2l)(s-r_2)}},\]

donde\(s = \frac{1}{2} (r_1 + r_2 + 2l)\). (Puede que desee referirse aquí a las fórmulas de las pp. 37 y 38 del Capítulo 2.)

De ahí\[ψ = - Gλ \ln \left[ \frac{r_1 + r_2 + 2l}{r_1 + r_2 -2l} \right]. \label{5.8.16} \tag{5.8.16}\]

Si\(r_1\) y\(r_2\) son muy grandes comparados con\(l\), son casi iguales, así que pongamos\(r_1 + r_2 = 2r\) y escribamos la Ecuación 5.8.17 como

\[ψ = -\frac{Gm}{2l} \ln \left[ \frac{2r \left( 1 + \frac{2l}{2r} \right)}{2r \left( 1 - \frac{2l}{2r} \right)} \right] = -\frac{Gm}{2l} \left[ \ln \left(1 + \frac{l}{r} \right) - \ln \left( 1 - \frac{l}{r} \right) \right] .\]

Maclaurin expande los logaritmos, y verás que, a grandes distancias de la varilla, el potencial es, esperado,\(−Gm/r\).

Volvamos a las inmediaciones de la vara y a la Ecuación\(\ref{5.8.16}\). Vemos que si nos movemos alrededor de la varilla de tal manera que nos mantenemos\(r_1 + r_2\) constantes e iguales a\(2a\), digamos − es decir, si nos movemos alrededor de la varilla en una elipse (ver nuestra definición de elipse en el Capítulo 2, Sección 2.3) − el potencial es constante. En otras palabras, los equipotenciales son elipses confocales, con los focos en los extremos de la varilla. La ecuación se\(\ref{5.8.16}\) puede escribir

\[ψ = - Gλ \ln \left( \frac{a+l}{a-l} \right) . \label{5.8.17} \tag{5.8.17}\]

Para un potencial dado\(ψ\), el equipotencial es una elipse del eje mayor

\[2a = 2l \left( \frac{e^{ψ/(Gλ)}+1}{e^{ψ/(Gλ)}-1} \right), \label{5.8.20} \tag{5.8.20}\]

donde\(2l\) esta la longitud de la varilla. Este conocimiento es útil si estás explorando el espacio y te encuentras con una nave espacial alienígena o un asteroide en forma de varilla uniforme de longitud\(2l\).