5.8.9: Esfera Sólida

Última actualización
Guardar como PDF

Page ID: 131392

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

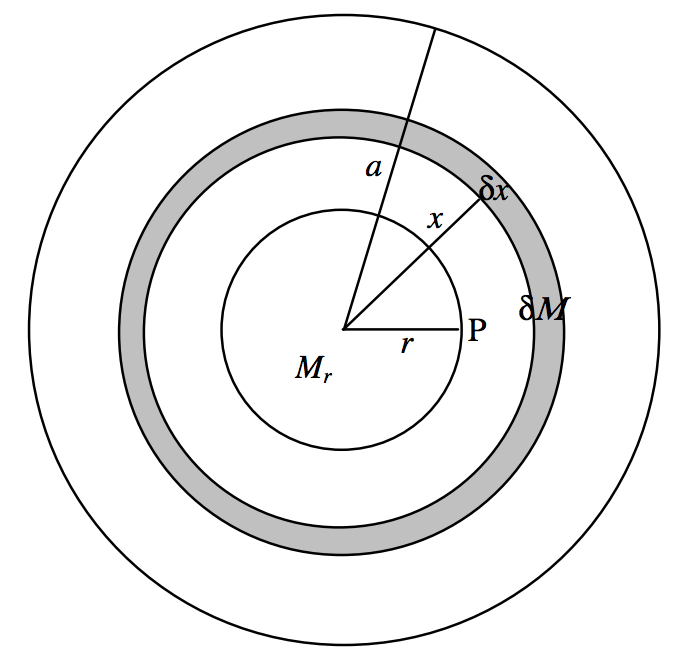
Figura V.24.png
\(\text{FIGURE V.24A}\)

El potencial fuera de una esfera sólida es igual que si toda la masa estuviera concentrada en un punto en el centro. Esto es así, aunque la densidad no sea uniforme, y siempre y cuando esté distribuida esféricamente. Vamos a encontrar el potencial en un punto\(\text{P}\) dentro de una esfera uniforme de radio\(a\), masa\(M\), densidad\(ρ\), a una\(r\) distancia del centro (\(r < a\)). Esto lo podemos hacer en dos partes. Primero, está el potencial de esa parte de la esfera “abajo”\(\text{P}\). Esto es\(-GM_r/r\), dónde\(M_r = \frac{r^3M}{a^3}\) está la masa dentro del radio\(r\). Ahora tenemos que tratar con el material “arriba”\(\text{P}\). Considerar una concha esférica de radios\(x\),\(x + δx\). Su masa es\(δM = \frac{4 \pi x^2 δx}{\frac{4}{3} \pi a^3} \cdot M = \frac{3Mx^2 δ x}{a^3}\). El potencial de este caparazón es\(-GδM/x = -\frac{3GMxδx}{a^3}\). Esto es para integrarse de\(x = 0\) a\(a\), y luego debemos agregar la contribución del material “abajo”\(\text{P}\). El resultado final es

\[ψ = -\frac{GM}{2a^3} \left(3a^2 - r^2 \right) . \label{5.8.23} \tag{5.8.23}\]

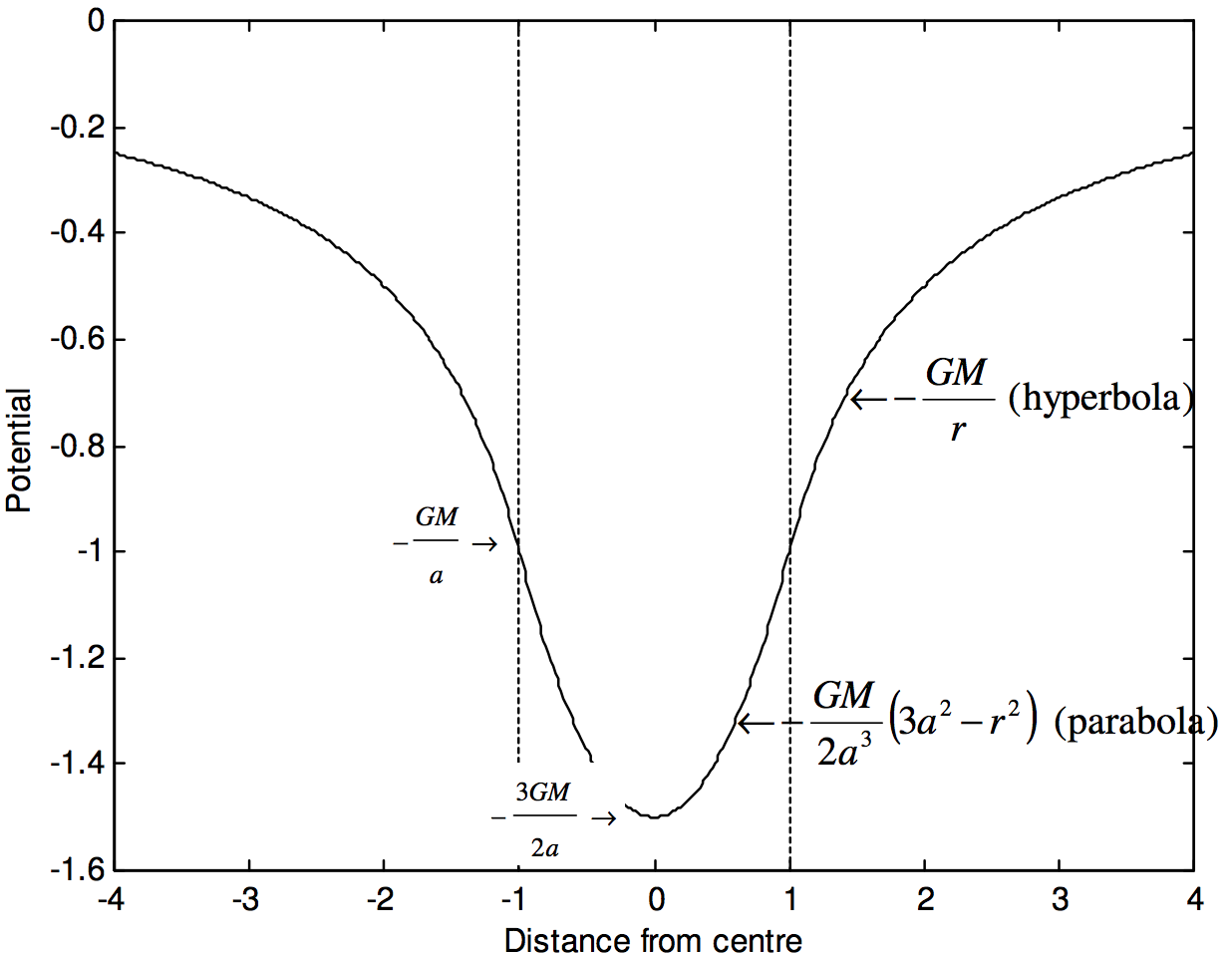
La figura\(\text{V.25}\) muestra el potencial tanto dentro como fuera de una esfera sólida uniforme. El potencial está en unidades del\(−GM/r\) radio de la esfera y la distancia en unidades del mismo.\(a\)

\(\text{FIGURE V.25}\)
Figura 5.25.png