5.12: Potencial gravitacional de cualquier Cuerpo Masivo
- Page ID
- 131323
Quizás solo quieras mirar el Capítulo 2 de Mecánica Clásica (Momentos de Inercia) antes de continuar con este capítulo.
En la figura\(\text{VIII.26}\) dibujo un cuerpo masivo cuyo centro de masa es\(\text{C}\), y un punto externo\(\text{P}\) a una distancia\(R\) de\(\text{C}\). Dibujo un conjunto de\(\text{C}xyz\) ejes, tal que\(\text{P}\) está en el\(z\) eje -eje, las coordenadas del\(\text{P}\) ser\((0, 0, z)\). Indico un elemento\(δm\) de masa, distante\(r\) de\(\text{C}\) y\(l\) de\(\text{P}\). Supondré que la densidad at\(δm\) es\(ρ\) y el volumen del elemento de masa es\(δτ\), así que eso\(δm = ρδτ\).
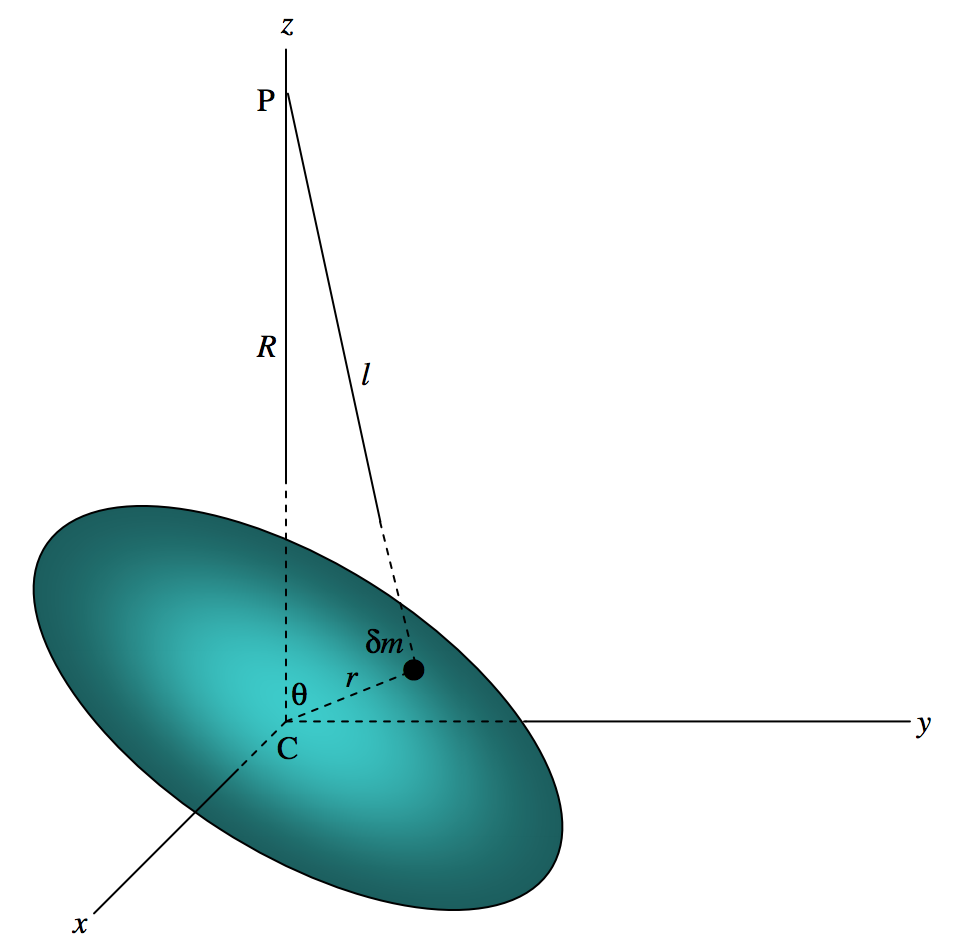
\(\text{FIGURE V.26}\)
El potencial en\(\text{P}\) es
\[ψ = -G \int \frac{dm}{l} = -G \int \frac{ρdτ}{l}. \label{5.12.1} \tag{5.12.1}\]
Pero\(l^2 = R^2 + r^2 - 2Rr \cos 2 θ\),
por lo\[ψ = -G \left[ \frac{1}{R} \int ρ dτ + \frac{1}{R^2} \int ρ r \cos θ d τ + \frac{1}{R^3} \int ρ r^2 P_2 (\cos θ) dτ + \frac{1}{R^4} \int ρ r^3 P_3 (\cos θ) d τ ... \right]. \label{5.12.2} \tag{5.12.2}\]
La integral es hacerse cargo de todo el cuerpo, de modo que\(∫ ρdτ = M\), donde\(M\) esta la masa del cuerpo. También\(∫ ρr \cos θd τ = \int z dm\), que es cero, ya que\(\text{C}\) es el centro de masa. El tercer término es
\[\frac{1}{2R^3} \int ρ r^2 (3 \cos^2 θ - 1) dτ = \frac{1}{2R^3} \int ρ r^2 (2-3\sin^2 θ ) dτ . \label{5.12.3} \tag{5.12.3}\]
Ahora
\[\int 2 ρ r^2 d τ = \int 2r^2 d m = \int \left[ (y^2 + z^2) + (z^2 + x^2) + (x^2 + y^2) \right] dm = A + B + C\]
donde\(A\),\(B\) y\(C\) son los segundos momentos de inercia con respecto a los ejes\(\text{C}x\)\(\text{C}y\),\(\text{C}z\) respectivamente. Pero\(A + B + C\) es invariante con respecto a la rotación de ejes, por lo que también es igual a\(A_0 + B_0 + C_0\), donde\(A_0, \ B_0, \ C_0\) están los principales momentos de inercia.
Por último,\(\int ρ r^2 \sin^2 θ dτ\) es igual a\(C\), el momento de inercia con respecto al eje\(\text{C}z\).
Así, si\(R\) es lo suficientemente mayor que\(r\) para que podamos descuidar términos de orden\((r/R)^3\) y superiores, obtenemos
\[ψ = - \frac{GM (2MR^2 + A_0 + B_0 + C_0 -3C)}{2R^3}. \label{5.12.4} \tag{5.12.4}\]
En el caso especial de una parte superior simétrica oblata, en la que\(A_0 = B_0 < C_0\), y la\(\text{CP}\) línea forma un ángulo\(γ\) con el eje principal, tenemos
\[C = A_0 + (C_0 - A_0) \cos^2 γ = A_0 + (C_0 - A_0) Z^2/R^2, \label{5.12.5} \tag{5.12.5}\]
para que\[ψ = -\frac{G}{R} \left[ M + \frac{C_0 - A_0}{2R^2} \left( 1 - \frac{3Z^2}{R^2} \right) \right]. \label{5.12.6} \tag{5.12.6}\]
Ahora considere un esferoide oblato uniforme de diámetros polares y ecuatoriales\(2c\) y\(2a\) respectivamente. Es fácil demostrar que
\[C_0 = \frac{2}{5} Ma^2. \label{5.12.7} \tag{5.12.7}\]
Ejercicio\(\PageIndex{1}\)
Confirmar Ecuación\ ref {5.12.7}.
Es un poco menos fácil de mostrar (Ejercicio: Muéstralo.) que
\[A_0 = \frac{1}{5} M \left( a^2 + c^2 \right) . \label{5.12.8} \tag{5.12.8}\]
Para una parte superior simétrica, las integrales de los polinomios impares de la ecuación\(\ref{5.12.2}\) son cero, y el potencial generalmente se escribe en la forma
\[ψ = - \frac{GM}{R} \left[ 1 + \left( \frac{a}{R} \right)^2 J_2 P_2 (\cos γ) + \left( \frac{a}{R} \right) J_4 P_4 (\cos γ) ... \right] \label{5.12.9} \tag{5.12.9}\]
Aquí\(γ\) está el ángulo entre\(\text{CP}\) y el eje principal. Para un esferoide oblato uniforme,\(J_2 = \frac{C_0 - A_0}{Mc^2}\). Este resultado será útil en un capítulo posterior cuando discutamos la precesión.


