6.4: Conversión entre coordenadas ecuatoriales y altazimutales

¿Paradero en el cielo estará una estrella determinada en un momento determinado? Esto como un problema típico que implica la conversión entre coordenadas ecuatoriales y altazimutales. Tenemos que resolver un triángulo esférico. Eso no es problema —ya sabemos cómo hacerlo. El problema es: ¿qué triángulo?

El primer problema, sin embargo, surge de la frase “en un momento determinado”. En particular, si queremos saber dónde está una estrella, por ejemplo, al 24 de noviembre de 2002, a las 10:00 p.m., hora estándar del Pacífico como se ve desde Victoria\(123^\circ \ 25^\prime.0 \ \text{W}\), cuya longitud es, necesitamos conocer la hora sideral local en ese instante.

El cálculo podría ir algo así.

Del Almanaque Astronómico encontramos que los tiempos siderales locales en Greenwich a\(0^\text{h}\)\(\text{UT}\) los días 25 y 26 de noviembre de 2002, son

25 de noviembre: 26\(04^\text{h} \ 16^\text{m} 59^\text{s}\)
de noviembre:\(04 \ \ \ 20 \ \ \ 56\)

Queremos el tiempo sideral local en noviembre\(24^\text{d} \ 22^\text{h} \ 00^\text{m} \ \text{PST}\)
= noviembre\(25^\text{d} \ 06^\text{h} \ 00^\text{m} \ \text{UT}\)

Por interpolación encontramos que el tiempo sideral local en Greenwich en ese instante es\(10^\text{h} \ 17^\text{m} \ 58^\text{s}\).

La longitud de Victoria es\(08^\text{h} \ 13^\text{m} \ 40^\text{s}\), y por lo tanto el tiempo sideral local en Victoria es\(02^\text{h} \ 04^\text{m} \ 18^\text{s}\).

Hemos superado el primer obstáculo, y ahora conocemos el tiempo sideral local (LST).

Nos preguntaremos ahora cuáles son la altitud y acimut de una estrella cuya ascensión y declinación correctas son\(α\) y\(δ\). También necesitamos la latitud del observador (= altitud del polo celeste norte), a la que voy a llamar\(\phi\). El ángulo horario\(H\) de la estrella es\(\text{LST}\) −\(α\).

El triángulo que tenemos que resolver es el triángulo\(\text{PZX}\). Aquí\(\text{P}\),\(\text{Z}\) y\(\text{X}\) están, respectivamente, el polo celeste norte, el cenit y la estrella. Es decir, resolvemos el triángulo formado por la estrella y los polos de los dos sistemas de coordenadas de interés. Dibujo la esfera celeste en figura\(\text{VI.3}\) vista desde el oeste. He marcado en el ángulo de la hora\(H\), la codeclinación\(90^\circ\) −\(δ\), la altitud\(\phi\) del polo, la distancia cenital\(z\) y el acimut\(A\) medido desde el punto norte hacia el oeste.

En triángulo\(\text{PZX}\), sabemos\(\phi\),\(δ\) y\(H\), así enseguida encontramos la distancia cenital\(z\) por aplicación de la fórmula coseno (Ecuación 3.5.2) y el acimut\(A\) de la fórmula cotangente (Ecuación 3.5.5).

Problema. Demostrar que el ángulo horario\(H\) de una estrella de declinación\(δ\) cuando se fija para un observador en latitud\(\phi\) viene dado por\(\cos H = − \tan δ \tan \phi\). Esto te permitirá ahora encontrar el Tiempo Sideral Local de Starset, ya que\(\text{LST} = \text{hour angle plus right ascension}\), y luego podrás convertir a tu zona hora solar.

Mostrar también que el acimut\(\text{A}\) de starset, hacia el oeste desde el punto norte, viene dado por\(\tan A = − \sin \phi \tan H\).

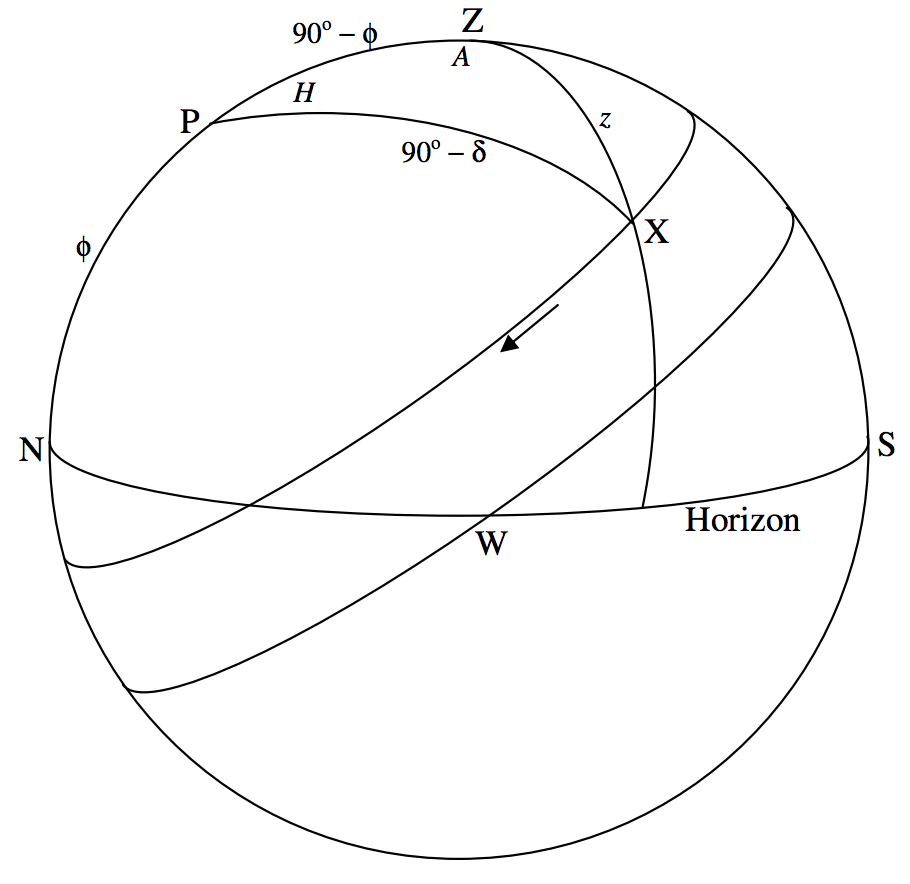
\(\text{FIGURE VI.3}\)