9.8: Elementos orbitales y vector de velocidad

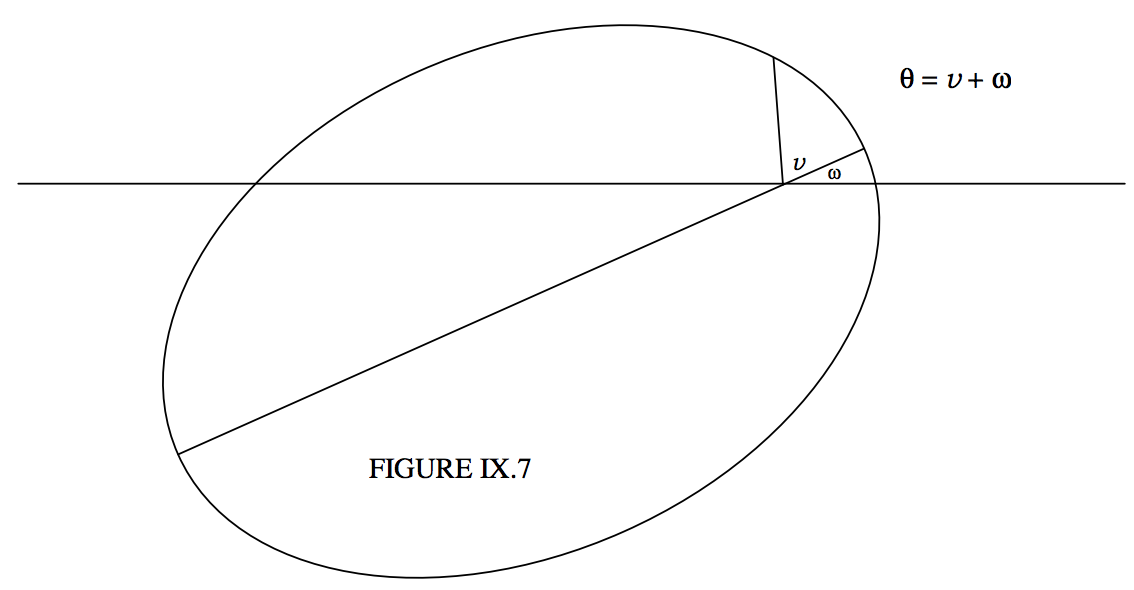
En dos dimensiones, una órbita puede ser completamente especificada por cuatro elementos orbitales. Tres de ellos dan el tamaño, forma y orientación de la órbita. Son, respectivamente,\(a\),\(e\) y\(ω\). Estamos familiarizados con el eje semi mayor\(a\) y la excentricidad\(e\). El ángulo\(ω\), el argumento del perihelio, se ilustró en la figura\(\text{II.19}\), la cual se reproduce aquí como figura\(\text{IX.7}\). Es el ángulo que hace el eje mayor con la línea inicial de las coordenadas polares. La figura nos\(\text{II.19}\) recuerda la relación entre el argumento del perihelio\(ω\), el argumento de latitud\(θ\) y la verdadera anomalía\(v\). Nos recordamos aquí la Ecuación a una sección cónica

\[r = \frac{l}{1 + e \cos v} = \frac{l}{1 + e \cos (θ-ω)}, \label{9.9.1} \tag{9.9.1}\]

donde el recto semi latus\(l\) es\(a(1 − e^2 )\) para una elipse, y\(a(e^2 − 1)\) para una hipérbola. Para una hipérbola, el parámetro a suele llamarse eje semitransversal. Para una parábola, el tamaño se describe generalmente por la distancia del perihelio\(q\), y\(l = 2q\).

El cuarto elemento es necesario para dar información sobre dónde se encuentra el planeta en su órbita en un momento determinado. Por lo general este es\(T\), el tiempo del paso del perihelio. En el caso de una órbita circular ésta no puede ser utilizada. En cambio, se podría dar el tiempo cuando\(θ = 0\), o el valor de\(θ\) en algún momento especificado.

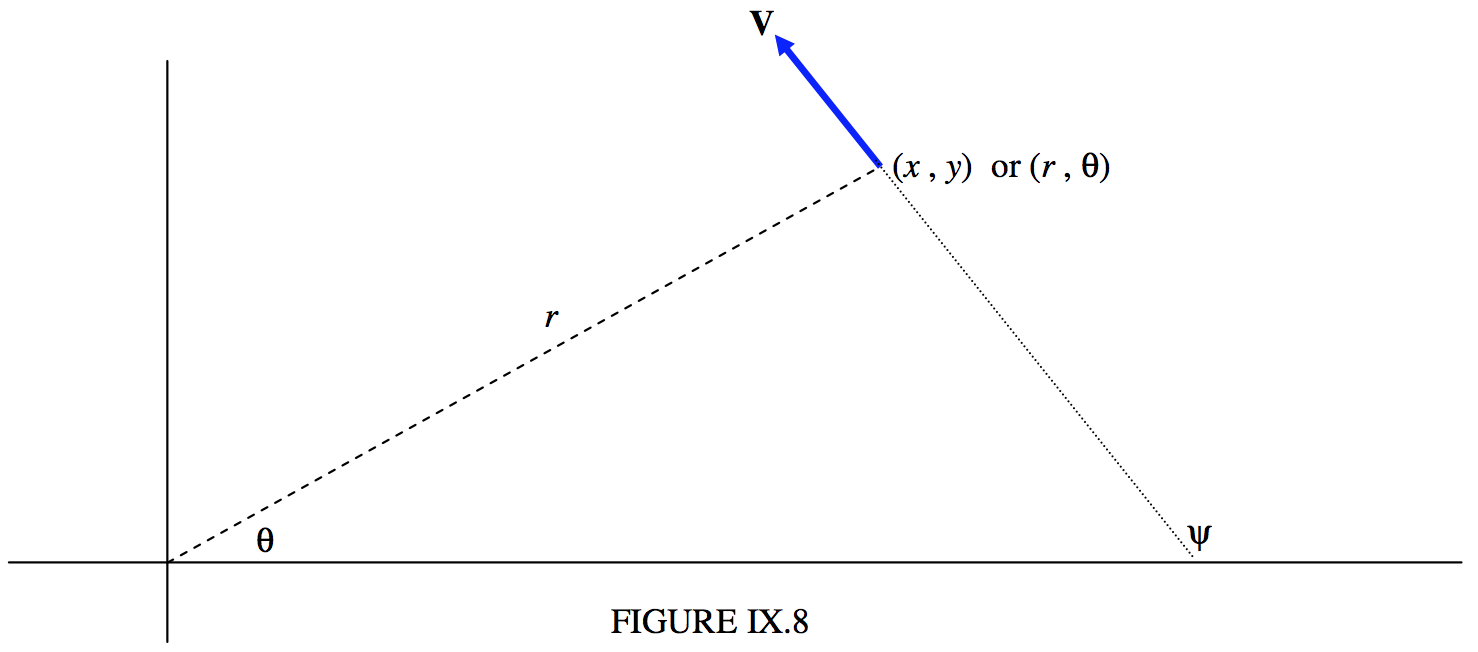
Refiérase ahora a la figura IX.8.

Supondremos que en algún momento\(t\) conocemos las coordenadas\((x , \ y)\) o\((r , \ θ)\) del planeta, y también la velocidad —es decir, la velocidad y dirección, o la\(x\) - y\(y\) - o los componentes radiales y transversales de la velocidad. Es decir, conocemos cuatro cantidades. Entonces se determina el camino posterior del planeta. En otras palabras, dadas las cuatro cantidades (dos componentes del vector de posición y dos componentes del vector de velocidad), deberíamos poder determinar los cuatro elementos\(a\),\(e\),\(ω\) y\(T\). Intentémoslo.

El eje semi mayor es fácil. Se determina a partir de la Ecuación\ ref {9.5.31}:

\[V^2 = G \textbf{M} \left( \frac{2}{r} - \frac{1}{a} \right) . \label{9.5.31} \tag{9.5.31}\]

Si las distancias se expresan en\(\text{AU}\) y si la velocidad se expresa en unidades de\(29.7846917 \ \text{km s}^{−1}\),\(G \textbf{M} = 1\), de modo que el semieje mayor en\(\text{AU}\) viene dado por

\[a = \frac{r}{2 - rV^2}. \label{9.9.2} \tag{9.9.2}\]

Es decir, si conocemos la velocidad y la distancia heliocéntrica, se conoce el eje semi mayor. Si\(a\) resulta ser infinita -en otras palabras, si\(V^2 = 2/r\) - la órbita es una parábola; y si\(a\) es negativa, es una hipérbola. Para una elipse, por supuesto, el periodo en años siderales viene dado por\(P^2 = a^3\).

A partir de la geometría de la figura\(\text{IX.8}\), el componente transversal de\(\textbf{V}\) es\(\text{V} \sin (ψ − θ)\), que se conoce, la magnitud y dirección de\(\textbf{V}\) presumirse conocida. Por lo tanto, el momento angular por unidad de masa es\(r\) multiplicado por esto, y, para una órbita elíptica, esto está relacionado con\(a\) y\(e\) por la Ecuación\ ref {9.5.27a}:

\[h = \sqrt{G \textbf{M} a(1 - e^2)}. \label{9.5.27a} \tag{9.5.27a}\]

\[r V \sin (ψ - θ) = \sqrt{G \textbf{M} a(1-e^2)} . \label{9.9.3} \tag{9.9.3}\]

Nuevamente, si las distancias se expresan\(\text{V}\) en\(\text{AU}\) y en unidades de\(29.7846917 \ \text{km s}^{−1}\)\(G \textbf{M} = 1\), y así

\[r V \sin (ψ - θ) = \sqrt{a(1 - e^2)}. \label{9.9.4} \tag{9.9.4}\]

Así\(e\) se determina.

La ecuación a una elipse es

\[ r = \frac{a(1 - e^2)}{1 + e \cos (θ - ω)}, \label{9.9.5} \tag{9.9.5}\]

por lo que, siempre y cuando se tenga el cuidado habitual en la elección del cuadrante, ahora\(ω\) se conoce.

A partir de ahí procedemos:

\[v = θ - ω, \quad \cos E = \frac{e + \cos v}{1 + e \cos v}, \quad \mathcal{M} = E - e \sin E = \frac{2π}{P}(t - T), \]

y\(T\) se encuentra. El procedimiento para una parábola o una hipérbola es similar.

Ejemplo\(\PageIndex{1}\)

A la vez\(t = 0\), un cometa está en\(x = +3.0\),\(y = +6.0 \ \text{AU}\) y tiene una velocidad con componentes\(\dot{x} = -0.2\),\(\dot{y}=+0.4\) tiempos\(29.7846917 \ \text{km s}^{−1}\). Encuentra los elementos orbitales\(a\),\(e\),\(ω\) y\(T\). (Por si te lo estás preguntando, una partícula de masa insignificante que se mueve alrededor del Sol en una órbita circular imperturbable de radio una unidad astronómica, se mueve con una velocidad de\(29.7846917 \ \text{km s}^{−1}\). Esto se desprende de la definición de la unidad astronómica de longitud.)

Solución

Anote en lo que sigue que, aunque estoy citando números a solo unas pocas cifras significativas, el cálculo en todo momento lleva las diez cifras que mi calculadora de mano permite. No obtendrás exactamente los mismos resultados a menos que hagas lo mismo. No redondear prematuramente. Estoy usando unidades astronómicas de distancia, años siderales por tiempo y velocidad en unidades de\(29.8 \ \text{km s}^{−1}\).

\[r = 6.708, \ θ = 63^\circ 26^\prime, \ V = 0.4472, \ ψ = 116^\circ 34^\prime\]

¡Asegúrate de acertar los cuadrantes!

\[\underline{a = 10.19 \ \text{AU}} \quad P = 32.5 \quad \underline{e = 0.6593} \quad \cos (θ − ω) = -0.21439\]

Y ahora nos encontramos ante un dilema. \(θ − ω = 102^\circ \ 23^\prime\)o\(257^\circ \ 37^\prime\). ¿Cuál es? Se trata de un típico “problema cuadrante”, y no se puede ignorar. Las dos posibles soluciones dan\(ω = 321^\circ \ 03^\prime\) o\(165^\circ \ 49^\prime\), y tenemos que decidir cuál es la correcta.

Las dos soluciones se dibujan en la Figura\(\text{IX.9}\). La curva continua es la elipse para\(ω = 321^\circ \ 03^\prime\) y la curva discontinua es la curva para\(ω = 165^\circ \ 49^\prime\). También he dibujado en el vector de velocidad at\((r , \ θ)\), y queda claro del dibujo que la curva continua con\(ω = 321^\circ \ 03^\prime\) es la elipse correcta. Ahora tenemos

\[\underline{ω = 321^\circ \ 03^\prime}\]

¿Hay alguna manera de deducir esto de las Ecuaciones en lugar de tomarse la molestia de dibujar las elipses? Ofrezco lo siguiente. Voy a encontrar la pendiente (gradiente) de cada elipse en el punto\(\text{P}\). La elipse correcta es aquella para la cual\(ψ = 116^\circ \ 34^\prime\), i.e\(dy/dx = −2\). La ecuación a la elipse es

\[r = \frac{1}{1 + e \cos (θ − ω)} = \frac{a(1-e^2)}{1 + e \cos (θ − ω)}, \label{9.9.6} \tag{9.9.6}\]

a partir de la cual\[\frac{dr}{dθ} = \frac{le \sin (θ − ω)}{[(1 + e \cos (θ − ω)]^2}. \label{9.9.7} \tag{9.9.7}\]

La expresión para\(\frac{dx}{dy} (= tanψ)\) en coordenadas polares es

\[\frac{dx}{dy} = \frac{\tan θ \frac{dr}{dθ} + r}{\frac{dr}{dθ} - r \tan θ}, \label{9.9.8} \tag{9.9.8}\]

y por supuesto\[r = \sqrt{x^2 + y^2}. \label{9.9.9} \tag{9.9.9}\]

De estos, obtengo, en nuestro ejemplo numérico,

para\(ω = 165^\circ \ 49^\prime , \ ψ = 190^\circ\), y para\(ω = 321^\circ \ 03^\prime , \ ψ = 165^\circ 49^\prime\),

por lo que claramente este último es correcto.

A partir de este punto vamos:

\[v = 102^\circ \ 23^\prime, \quad \cos E = 0.51817,\]

y nuevamente se nos presenta un dilema, para esto da\(E = 58^\circ \ 47^\prime\) o\(301^\circ \ 13^\prime\), y tenemos que decidir cuál es el correcto. Desde el significado geométrico de\(v\) y\(E\), podemos entender que son iguales cuando cada uno de ellos es\(0^\circ\) o\(180^\circ\). Ya que\(v < 180^\circ\), también\(E\) debe ser menor que\(180^\circ\), por lo que la elección correcta es\(E = 58^\circ \ 47^\prime = 1.0261 \ \text{rad}\). A partir de ahí, tenemos

\[\mathcal{M} = 26^\circ \ 29^\prime = 0.46218 \ \text{rad}, \quad \underline{T = -2.392 \text{sidreal years},}\]

y los elementos están ahora completamente determinados.

Ejercicio\(\PageIndex{1}\)

Escriba un programa de computadora, en el idioma de su elección, en el que estén los datos de entrada\(x, \ y, \ \dot{x}, \ \dot{y}\), y la salida sea\(a, \ e, \ ω\) y\(T\). Probablemente querrás mantenerlo simple al principio, y lidiar solo con elipses. Por lo tanto, si el programa calcula que eso no\(a\) es positivo, salga del programa entonces. No estoy seguro de cómo va a resolver los problemas del cuadrante. Eso estará a la altura de tu ingenio. No olvides que muchos idiomas tienen una\(\text{ARCTAN2}\) función. Posteriormente, querrás ampliar el programa y tratar con cualquier conjunto de\(x, \ y, \ \dot{x}, \ \dot{y}\), con una órbita resultante que puede ser cualquiera de las secciones cónicas. Casos particularmente molestos pueden ser aquellos en los que el planeta se dirige recto hacia el Sol, sin componente transversal de velocidad, de manera que se mueve en línea recta, o una órbita circular, en cuyo caso no\(T\) está definido.

Observe que el problema que hemos tratado en esta sección es lo opuesto al problema que tratamos en las Secciones 9.6, 9.7 y 9.8. En este último, nos dieron los elementos, y calculamos la posición del planeta en función del tiempo. Es decir, calculamos una efemérides. En la presente sección, se nos da la posición y la velocidad en algún momento y se nos pide que calculemos los elementos. Ambos problemas son de dificultad comparable. Quizás este último sea un poco más fácil que el primero, ya que no tenemos que resolver la Ecuación de Kepler. Esto podría dar la impresión de que calcular los elementos orbitales de un planeta es de dificultad comparable a, o incluso un poco más fácil que, calcular una efemérides a partir de los elementos. Esto está, en la práctica, muy lejos del caso, y de hecho calcular los elementos a partir de las observaciones es mucho más difícil que generar una efemérides. En esta sección, hemos calculado los elementos, dados los vectores de posición y velocidad. En la vida real, cuando un nuevo planeta nada en nuestro ken, no tenemos idea de la distancia o de la velocidad o la dirección del movimiento. Todo lo que tenemos es un conjunto de posiciones contra el fondo estrellado, y la parte más difícil del problema de determinar los elementos es determinar la distancia.

El siguiente capítulo tratará de generar una efemérides (ascensión derecha y declinación en función del tiempo) a partir de los elementos orbitales en la situación tridimensional real. El cálculo de los elementos a partir de las observaciones vendrá mucho más tarde.