11.3.3: Refracción

La refracción de la luz estelar a medida que pasa a través de la atmósfera terrestre desplaza la posición de la estrella hacia el cenit. La cantidad de la refracción no es grande cerca del cenit, sino que asciende a aproximadamente medio grado cerca del horizonte. La atmósfera de la Tierra no es más que una piel delgada comparada con el radio de la Tierra, y, siempre que la estrella no esté cerca del horizonte, podemos tratar a la atmósfera como una atmósfera plano-paralela. La situación se ilustra en la figura\(\text{XI.5}\).

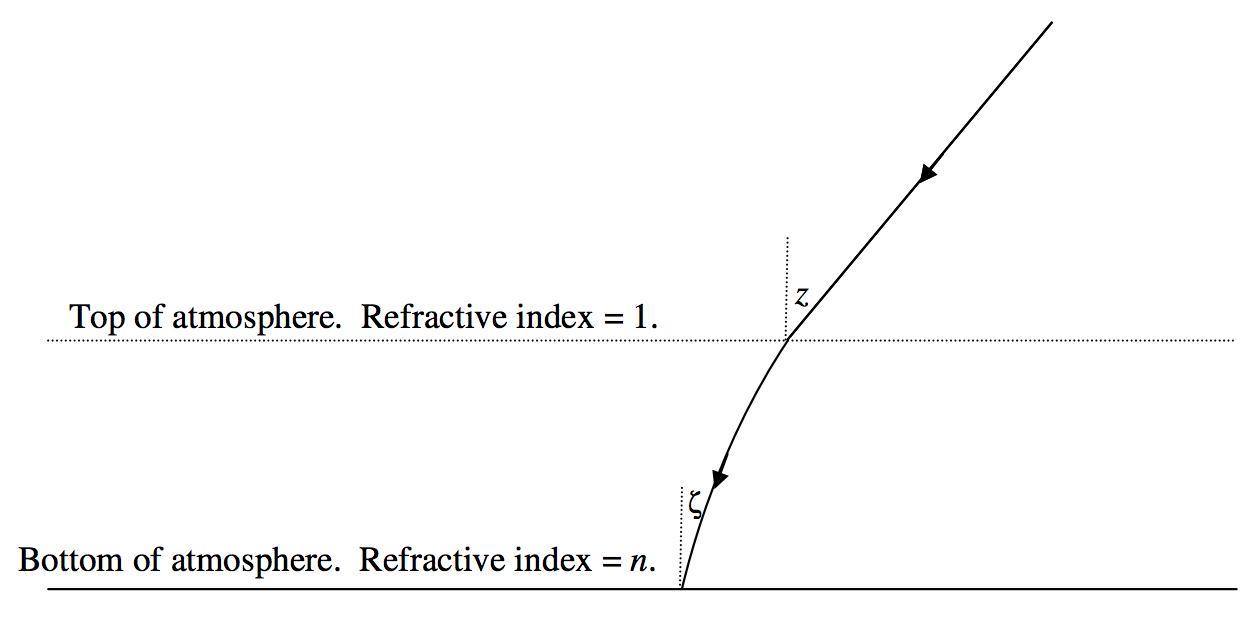
\(\text{FIGURE XI.5}\)

El ángulo\(z\) es la verdadera distancia cenital, es decir, la distancia cenital que tendría en ausencia de una atmósfera. El ángulo\(ζ\) es la distancia cenital aparente. Por aplicación de la ley de Snell, tenemos\(\sin z = n\sin ζ\), y si lo dejamos\(ε = z − ζ\), esto se convierte en

\[\sin ζ \cos ε + \cos ζ \sin ε = n \sin ζ . \label{11.3.1} \tag{11.3.1}\]

Dividir ambos lados por\(\sin ζ\) y hacer las aproximaciones (correctas a primer orden en\(ε\))\(\sin ε ≈ ε\)\(\cos ε ≈ 1\), y obtenemos

\[ε = z - ζ = (n-1) \tan ζ . \label{11.3.2} \tag{11.3.2}\]

El índice de refracción a nivel del suelo varía un poco con la temperatura y la presión, pero promedia aproximadamente\(n − 1 = 58^".2\). (No sabías que el índice de refracción se expresaba en segundos de arco, ¿verdad?)

Hemos hecho algunas aproximaciones en la derivación de la Ecuación\ ref {11.3.2}, pero hay que tener en cuenta que, en lo que respecta a la astrometría, lo importante es la refracción diferencial entre la parte inferior y la parte superior del detector (película fotográfica o\(\text{CCD}\)), y la Ecuación\ ref {11.3.2} debería ser más que adecuado — a menos que uno esté observando muy cerca del horizonte. El único momento en el que es probable que uno esté observando cerca del horizonte sería para un cometa brillante, para lo cual es muy difícil hacer mediciones precisas de todos modos. La refracción diferencial entre la parte superior e inferior obviamente equivale a

\[δε = (n-1) \sec^2 ζ δζ , \label{11.3.3} \tag{11.3.3}\]

donde\(δζ\) está el rango de distancia cenital cubierto por el detector. En la siguiente tabla muestro la refracción diferencial entre la parte superior e inferior de un detector (como una película fotográfica) con un campo de 5 grados, y para un detector (como a\(\text{CCD}\)) con un campo de 20 minutos de arco, para cuatro distancias cenitales. Obviamente, la corrección para la refracción diferencial debe hacerse para el campo fotográfico de 5 grados. Se podría argumentar que, para el campo relativamente pequeño de un minuto de arco de 20\(\text{CCD}\), la corrección para la refracción diferencial no es importante. Sin embargo, la precisión esperada para la\(\text{CCD}\) astrometría moderna es bastante mayor que la precisión que se esperaba durante la era fotográfica, y ciertamente, para grandes distancias cenitales, si se espera una astrometría de subarcsegundo, es deseable una corrección para la refracción diferencial. Tengan en cuenta, también, que los CCD son cada vez más grandes a medida que avanza la tecnología, y que cuanto más grande sea el CCD, más importante será la corrección de la refracción.

\ begin {array} {c c c}
\ texto {distancia cenital} & δε\\ texto {en segundos de arco} & δε\\ texto {en segundos de arco}
\\ texto {en grados} &\ texto {para} 5^\ circ\ texto {campo} &\ texto {para} 20^\ prime\ texto {campo}\
\\
15 y 5.5 y 0.4\\
30 & 6.8 & 0.5\\
45 & 10.2 & 0.7\\
60 & 20.4 & 1.4\\
\ end {array}

La forma más directa de corregir la refracción diferencial es calcular la verdadera distancia cenital\(z\) y acimut\(A\) de cada estrella de comparación mediante los métodos habituales de astronomía esférica:

\[\cos z = \sin \phi \sin δ + \cos \phi \cos δ \cos H \label{11.3.4} \tag{11.3.4}\]

y\[ \tan A = \frac{\sin H}{\cos \phi \tanδ - \sin \phi \cos H}. \label{11.3.5} \tag{11.3.5}\]

Aquí\(\phi\) está la latitud del observador, y\(H\) es el ángulo horario de la estrella, que se encuentra desde su ascensión correcta y el tiempo sideral local. Habiendo encontrado\(z\), entonces calcula la distancia cenital aparente\(ζ\) de la Ecuación\ ref {11.3.2} (la refracción no cambia, por supuesto, el acimut), y luego invertir las Ecuaciones\ ref {11.3.4} y\ ref {11.3.5} para obtener el ángulo aparente de la hora\(H^\prime\) (y por lo tanto aparente ascensión derecha\(α^\prime\)) y aparente declinación\(δ^\prime\) de la estrella. Haz esto para todas las estrellas de comparación. (A mano, esto puede sonar largo y tedioso, pero claro que cuando una computadora está programada para hacerlo, es todo automático e instantáneo).

\[\sin δ^\prime = \sin \phi \cos ζ + \cos \phi \sin ζ \cos A \label{11.3.6} \tag{11.3.6}\]

y\[\tan H^\prime = \frac{\sin A \tan ζ}{\cos \phi - \sin \phi \cos A \tan ζ}. \label{11.3.7} \tag{11.3.7}\]

Después se pueden realizar las mediciones y a partir de ellas calcular la aparente ascensión derecha y declinación del asteroide. A partir de estos, calcular la distancia cenital aparente. Corrija esto para obtener la verdadera distancia cenital, y finalmente calcular la verdadera ascensión correcta y declinación del asteroide —nuevamente todo esto se hace instantáneamente una vez que haya programado correctamente la computadora.

Otro aspecto de la refracción que podría considerarse es que las estrellas azules (de tipo temprano) se refractan más que las estrellas rojas (de tipo tardío). En principio, por lo tanto, se deben usar solo estrellas de comparación que sean del mismo color que el asteroide. En la práctica, me imagino que pocos astrometristas siempre hacen esto. Si, por desgracia, una de las estrellas de comparación es muy roja o muy azul, esto puede resultar en un gran residuo para esa estrella, y la estrella puede ser detectada y rechazada, como se describe en la subsección\ ref {11.3.6}. Otro aspecto más es que, debido a la dispersión, la luz de la estrella —especialmente si está baja cerca del horizonte— será dibujada en un espectro corto, con el extremo rojo más cerca del horizonte que el extremo azul, y entonces hay un problema de cómo medir la posición de la estrella. La respuesta es probablemente dejar asteroides que están cerca del horizonte a observadores que se encuentran en una latitud más favorable. Como se mencionó anteriormente, la única vez que es probable que observe muy abajo sería para un cometa de largo periodo, en el que no se puede establecer de manera extremadamente precisa en ningún caso.