11.3.4: Aberración de la Luz

Por “aberración” no me refiero a aberraciones ópticas producidas por lentes y espejos, como el coma y el astigmatismo y aberraciones ópticas similares, sino a la aberración de la luz resultante de la diferencia vectorial entre la velocidad de la luz y la velocidad de la Tierra. (En estas notas, la palabra “velocidad” se usa para significar “velocidad” y la palabra “velocidad” se usa para significar “velocidad”. La palabra “velocidad” no debe ser utilizada simplemente como una palabra más larga e impresionante para “velocidad”.)

El efecto de la aberración es desplazar una estrella hacia el Apex del Camino de la Tierra, que es el punto en la esfera celeste hacia la que se mueve la Tierra. El ápice es donde la eclíptica cruza el meridiano del observador a las 6 horas de tiempo solar aparente local. La cantidad del desplazamiento aberracional varía con la posición en el cielo, siendo mayor para las estrellas\(90^\circ\) del ápice. Es entonces de magnitud\(v/c\), donde\(v\) y\(c\) son las velocidades de la Tierra y de la luz respectivamente. Esto equivale a 20.5 segundos de arco. (No sabías que la velocidad de la Tierra podría expresarse en segundos de arco, ¿verdad?) Pero lo que importa en astrometría es la aberración diferencial entre un borde del detector (película fotográfica o\(\text{CCD}\)) y el otro. Evidentemente este va a ser un efecto mucho menor que la refracción diferencial.

Examinemos el efecto de la aberración en cifras\(\text{XI.6a}\) y\(\text{b}\).

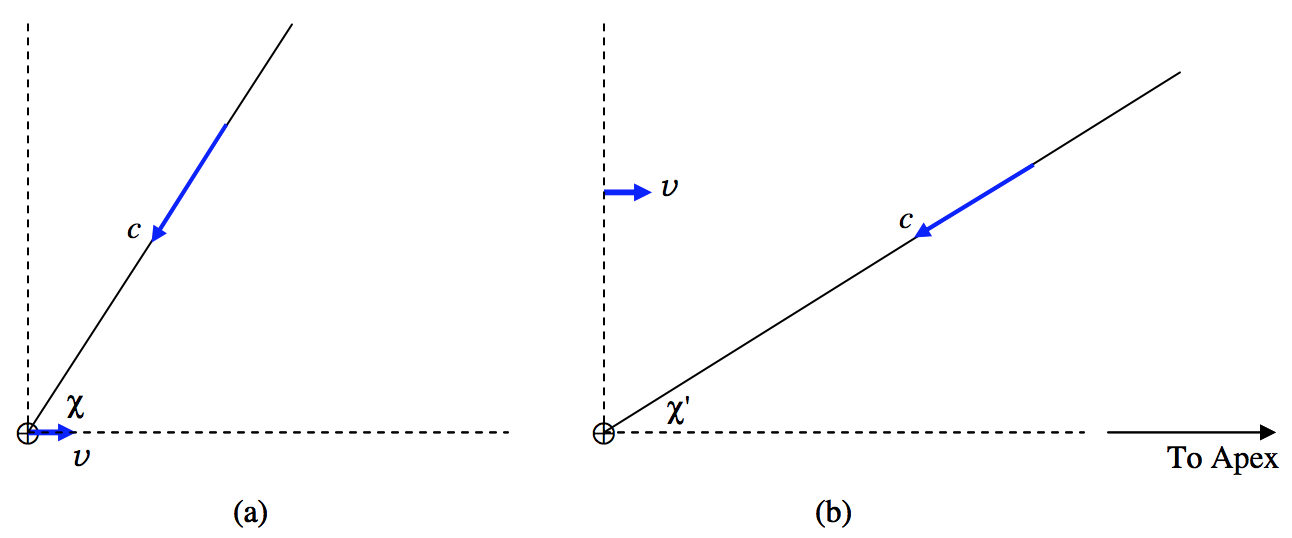
\(\text{FIGURE XI.6}\)

La parte (a) de la figura muestra un marco de referencia estacionario. Por “estacionario” me refiero a un marco en el que la Tierra\(\oplus\),, se mueve hacia el ápice a velocidad\(v = 29.8 \ \text{km s}^{−1}\). La luz de una estrella se acerca a la Tierra a velocidad\(c\) desde una dirección que hace un ángulo\(χ\), que llamaré la verdadera distancia apical, con la dirección hacia el ápice.

La parte (b) muestra la misma situación referida a un marco en el que la Tierra está estacionaria; es decir, el marco (b) se mueve hacia el ápice con velocidad\(v\) relativa al marco (a). Referido a este marco, la velocidad de la luz es\(c\), y viene de una dirección\(χ^\prime\), a la que llamaré la aparente distancia apical.

Me refiero a la diferencia\(ε = χ − χ^\prime \) como el desplazamiento aberracional.

Por brevedad me referiré a la dirección al ápice como la “\(x\)-dirección” y la dirección hacia arriba en las figuras como la “\(y\)-dirección”.

Referido al marco (a), el\(x\) -componente de la velocidad de la luz es\(− c \cos χ\), y referido al marco (b), el\(x\) -componente de la velocidad de la luz es\(− c \cos χ^\prime\). Estos están relacionados por la transformación de Lorentz entre componentes de velocidad:

\[c \cos χ^\prime = \frac{c \cos χ + v}{1 + (v/c) \cos χ}. \label{11.3.8} \tag{11.3.8}\]

Referido al marco (b), el componente y de la velocidad de la luz es\(− c \sin χ\), y referido al marco (b), el\(y\) -componente de la velocidad de la luz es\(− c \sin χ^\prime\). Estos están relacionados por la transformación de Lorentz entre componentes de velocidad:

\[c \sin χ^\prime = \frac{c \sin χ}{γ \left( 1 + (v/c) \cos χ \right)}, \label{11.3.9} \tag{11.3.9}\]

en el que, de ser necesario, a se\(c\) puede cancelar desde cada lado de la Ecuación. En la Ecuación\ ref {11.3.9},\(γ\) se encuentra el factor Lorentz\(1 / \sqrt{1-(v/c)^2}\).

Las ecuaciones 11.3.8 y 9 no son independientes; efectivamente una puede considerarse como otra forma de escribir la otra. Una manera fácil de mostrar esto, por ejemplo, es demostrarlo\(\sin^2 χ^\prime + \cos^2 χ^\prime = 1\). En todo caso, cualquiera de ellos da\(χ^\prime\) en función de\(χ\) y\(v /c\).

La figura\(\text{XI.7}\) muestra\(χ^\prime\) como una función de\(χ\) for\(v /c = 0.125, \ 0.250, \ 0.375, \ 0.500, \ 0.625, \ 0.750\) y\(0.875\).

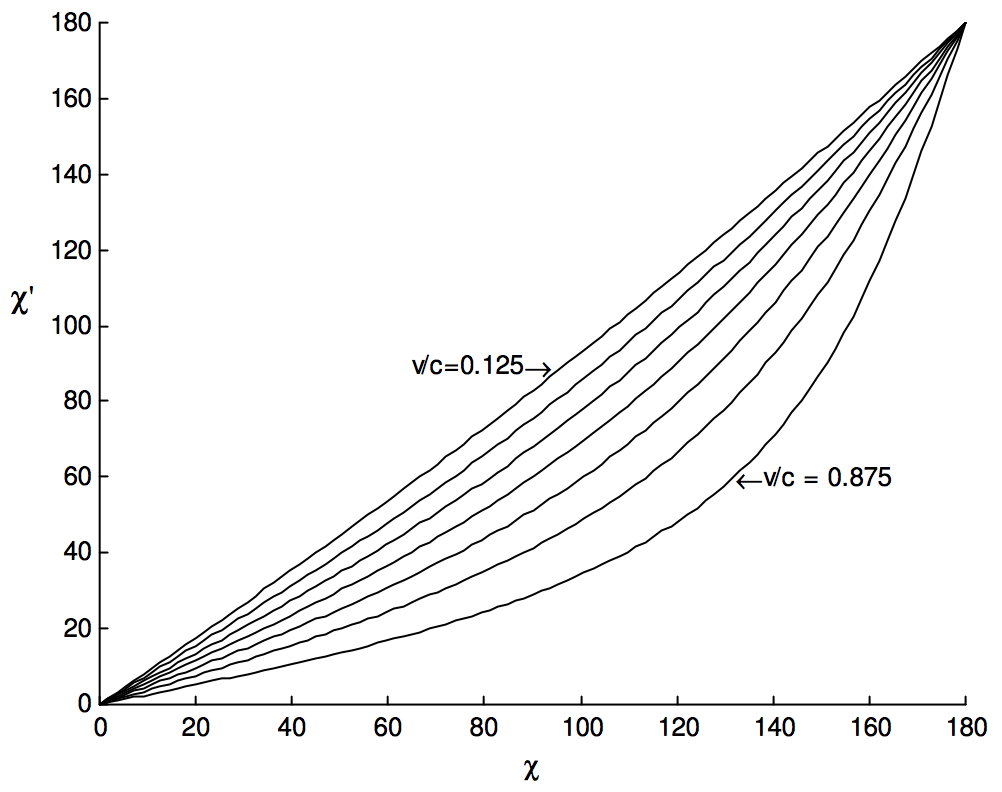
\(\text{FIGURE XI.7}\)

Para la Tierra en órbita alrededor del Sol,\(v = 29.8 \ \text{km s}^{−1}\) y\(v/c = 9.9 \times 10^{−5}\), que corresponde a un ángulo de\(20^{\prime \prime} .5\). Así, el desplazamiento aberracional es muy pequeño. Si escribimos\(ε = χ − χ^\prime\), la Ecuación\ ref {11.3.8} toma la forma a primer orden en\(ε\):

\[\cos (χ - ε) = \cos χ + ε\sin χ = \frac{\cos χ + (v/c)}{1 + (v/c) \cos χ}, \label{11.3.10} \tag{11.3.10}\]

de la que, después de un álgebra muy poco, encontramos

\[ε = \frac{(v/c) \sin χ}{1 + (v/c) χ}, \label{11.3.11} \tag{11.3.11}\]

o, desde\(v/c << 1,\)

\[ ε \approx \frac{v \sin χ}{c}, \label{11.3.12} \tag{11.3.12}\]

Así vemos que el desplazamiento aberracional es cero en el ápice y en el antápice, y alcanza su mayor valor,\(20^{\prime \prime} .5\), noventa grados desde el ápice.

Al igual que con la refracción, sin embargo, es la aberración diferencial la que cuenta, y si el diámetro del campo detector es\(δχ\), la diferencia\(δε\) en el desplazamiento aberracional a través del campo es

\[δε = \frac{v \cos χδχ}{c}. \label{11.3.13} \tag{11.3.13}\]

Observe que la aberración diferencial es mayor en el ápice y el antápice, y es cero noventa grados del ápice. Cabe señalar que el punto de oposición, donde quizás se realizan la mayoría de las observaciones de asteroides, se encuentra a noventa grados del ápice.

La siguiente tabla, similar a la mostrada para la refracción diferencial, muestra la aberración diferencial en campos de cinco grados y 20 minutos de arco para diversas distancias apicales.

\ begin {array} {c c c}
\ text {distancia apical} & δε\\ texto {en segundos de arco} & δε\\ texto {en segundos de arco}
\\ texto {en grados} &\ texto {para} 5^\ circ\ texto {campo} &\ texto {para} 20^\ prime\ texto {campo}
\\\
0 & 1.8 y 0.12\
15 & 1.7 & 0.12\\
30 & 1.5 & 0.10\\
45 & 1.3 & 0.09\\
60 & 0.9 & 0.06\\
90 & 0.0 & 0.00\
\ end {array}

Se podría concluir que el efecto de la aberración diferencial es tan pequeño que apenas merece la pena preocuparse en la mayoría de las circunstancias. Sin embargo, las expectativas para la precisión de la astrometría de asteroides son ahora bastante estrictas y es probable que se vuelvan más exigentes a medida que avance el tiempo, y para un trabajo preciso se debe hacer la corrección. Uno de los problemas con los programas de astrometría preempaquetados es que el usuario no siempre sabe qué correcciones se incluyen en el paquete. La forma más segura es hacerlo uno mismo.

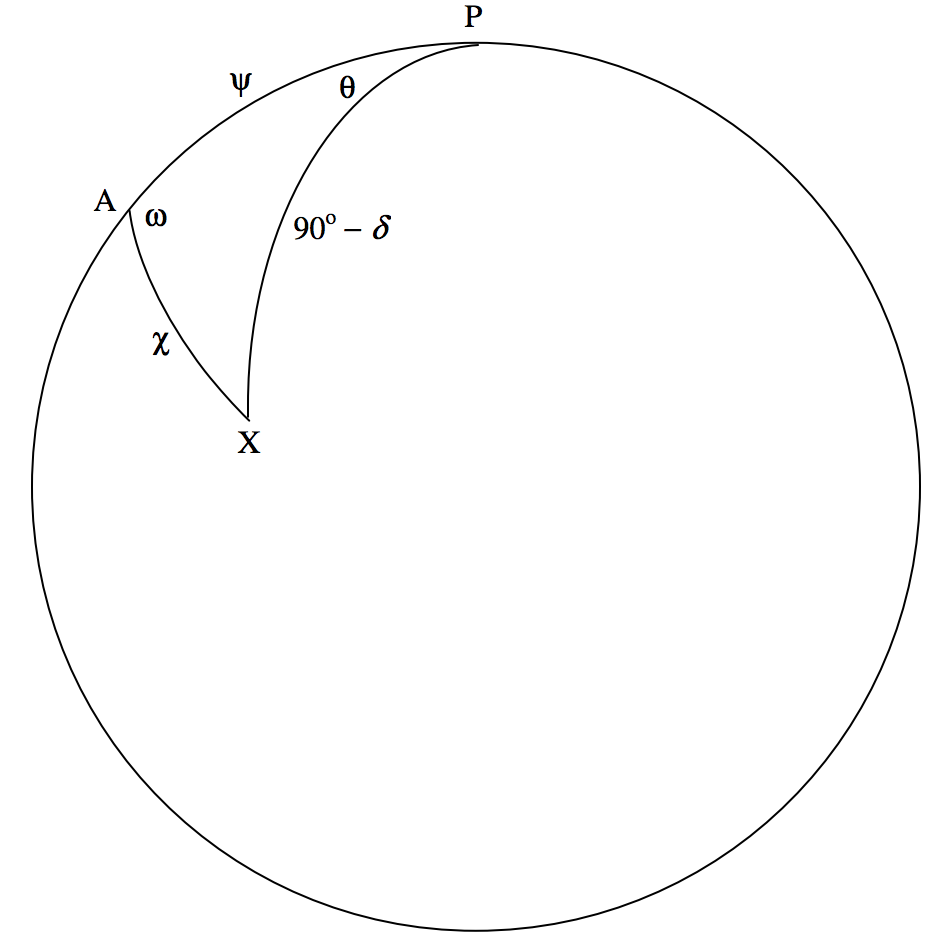
\(\text{FIGURE XI.8}\)

En la figura\(\text{XI.8}\),\(\text{P}\) es el polo celeste norte,\(\text{A}\) es el vértice del camino de la Tierra, y\(\text{X}\) es una estrella de verdaderas coordenadas ecuatoriales\((α , \delta)\). La distancia apical\(\text{AX}\) es\(χ\). El ángulo θ es α (X) − α (A), el ángulo\(\text{PAX}\) es\(ω\), y\(ψ\) es la distancia del polo al ápice. Se supone que el observador sabe calcular ω y ψ mediante las fórmulas habituales de astronomía esférica, y de ahí que todos los ángulos en figura\(\text{XI.8}\) son conocidos.

De la fórmula cotangente, tenemos

\[\cos ψ \cos ω = \sin ψ \cot χ - \sin ω \cos θ . \label{11.3.14} \tag{11.3.14}\]

Si\(χ\) se incrementa en\(δχ\), el incremento correspondiente en\(θ\) viene dado por

\[\sin ω \sin θδθ = \sin ψ \csc^2 χδχ . \label{11.3.15} \tag{11.3.15}\]

Aquí\(δθ = α^\prime (\text{X}) − α(\text{X})\), dónde\(α\) y\(α^\prime\) son, respectivamente, las verdaderas y aparentes ascensiones derechas de la estrella, y\(δχ\) es\(χ^\prime − χ\), que es\(−ε\). Es fácil errar en señal en este punto, así que reescribo la Ecuación\ ref {11.3.15} de manera más explícita:

\[ \left( α^\prime (X) - α(X) \right). \sin ω . \sin \left( α (X) - α (P) \right) = - ε \sin ψ \csc^2 χ . \label{11.3.16} \tag{11.3.16}\]

Aquí\(ε\) está el desplazamiento aberracional de\(\text{X}\) hacia\(\text{A}\) dado por la Ecuación\ ref {11.3.12}. Al sustituir la Ecuación\ ref {11.3.12} en la Ecuación\ ref {11.3.16}, esto se convierte, entonces,

\[\left( α^\prime (X) - α(X) \right) . \sin ω . \sin \left( α (X) - α (P) \right) = -\frac{v}{c} \sin ψ \csc χ. \label{11.3.17} \tag{11.3.17}\]

Esto nos permite calcular la aparente ascensión correcta de la estrella.

La declinación se obtiene de una aplicación de la fórmula coseno:

\[\sin \delta = \cos χ \cos ψ + \sin χ \sin ψ \cos ω, \label{11.3.18} \tag{11.3.18}\]

a partir de la cual

\[\cos \delta δ \delta = \left( - \cos ψ \sin χ + \sin ψ \cos ω \cos χ \right) δχ. \label{11.3.19} \tag{11.3.19}\]

Aquí nuevamente, como en la convención habitual del cálculo,\(δχ\) representa un incremento de\(χ\) y\(δ \delta\) es el incremento correspondiente en\(\delta\). Pero la aberración resulta en una disminución de la distancia apical, así que eso\(δχ = −ε\).

La ecuación 11.3.19 nos permite calcular la declinación aparente de la estrella.

A partir de las mediciones de las posiciones de las estrellas de comparación y el asteroide, ahora podemos calcular la aparente ascensión derecha y declinación del asteroide, y, por inversión de Ecuaciones\ ref {11.3.17} y 11.3.19, podemos determinar la verdadera ascensión y declinación correctas del asteroide.