15.3: Las ecuaciones del movimiento

Primero consideremos el movimiento de un asteroide solo bajo la influencia gravitacional del Sol, ignorando las perturbaciones de los otros planetas. Tomamos la masa del Sol para ser M y la masa del asteroide para ser m. La fuerza sobre el asteroide − y, por supuesto, por la tercera ley de Newton, la fuerza sobre el Sol − es\( \frac{G M m}{r^{2}}\), donde r es la distancia entre los dos cuerpos. Los dos cuerpos están, por supuesto, en movimiento alrededor de su centro de masa común, que, en el caso de un asteroide, se encuentra muy cerca del centro del Sol.

La aceleración del asteroide hacia el centro de masa es\(\frac{G M}{r^{2}}\), y la aceleración del Sol hacia el centro de masa es\(\frac{G m}{r^{2}}\). Si referimos el movimiento al Sol como origen, vemos que la aceleración del asteroide hacia el Sol es\( \frac{G(M+m)}{r^{2}}\). En forma vectorial podemos escribir esto como

\[\ddot{\mathbf{r}}=-\frac{G(M+m)}{r^{3}} \mathbf{r},\]

donde r es un vector dirigido desde el Sol hacia el asteroide, con componentes rectangulares heliocéntricos (x, y, z). Estas coordenadas heliocéntricas podrían ser coordenadas eclípticas, para las cuales hasta ahora hemos utilizado los símbolos (X, Y, Z); o bien podrían ser coordenadas ecuatoriales, para las que hasta ahora hemos utilizado los símbolos (, η,). Los símbolos (x, y, z) se entenderán aquí para referirse a cualquiera, a nuestra conveniencia. Es más probable que tengamos disponibles las coordenadas ecuatoriales en lugar de las eclípticas. Los cosenos de dirección de r son\( \left(\frac{x}{r}, \frac{y}{r}, \frac{z}{r}\right)\), y consecuentemente los componentes rectangulares de la Ecuación 15.3.1 son

\[ \ddot{x}=-\frac{G(M+m)}{r^{3}} x\]

\[ \ddot{y} =-\frac{G(M+m)}{r^{3}} y\]

\[\ddot{z} =-\frac{G(M+m)}{r^{3}} z\]

Estas son las Ecuaciones de movimiento del asteroide con respecto al Sol como origen. Las cantidades\(x, y, z, r\left(=\sqrt{x^{2}+y^{2}+z^{2}}\right)\) son, por supuesto, funciones del tiempo. La solución de estas Ecuaciones describe las órbitas elípticas (u otras secciones cónicas) del asteroide y todas las demás propiedades que hemos discutido en capítulos anteriores.

Si estamos usando coordenadas eclípticas (X, Y, Z), el eje X se dirige hacia el Primer Punto de Aries, el eje Y se dirige a lo largo de la dirección de longitud eclíptica creciente, y el eje Z se dirige hacia el polo norte de la eclíptica.

Si estamos usando coordenadas ecuatoriales (, η,), el eje se dirige hacia el Primer Punto de Aries, el eje ηse dirige en la dirección de 6 horas de ascensión derecha, y el eje se dirige hacia el polo celeste norte. La Tierra estará en el eje X o en septiembre (no en marzo).

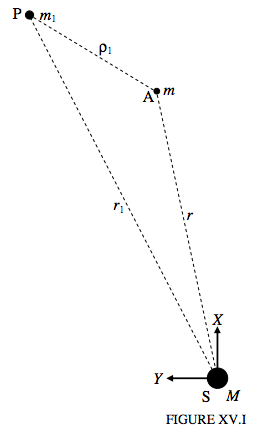
Ahora introduzcamos un tercer cuerpo, un planeta perturbador, como, quizás, Júpiter. Supondremos que su masa es m ₁, que su distancia del Sol es r ₁ y su distancia del asteroide es ρ ₁ (ver figura XV.I, en la que S es el Sol, A es el asteroide y P es el planeta perturbador). Este es ahora un problema de tres cuerpos y una solución general en términos de funciones algebraicas no es posible, y tiene que resolverse mediante cómputos numéricos.

Además de las aceleraciones del asteroide hacia el Sol y del Sol hacia el asteroide descrito en la página 3, utilizadas en el desarrollo de las Ecuaciones 15.3.1-4, ahora también tenemos que considerar las aceleraciones del asteroide y del Sol hacia el planeta perturbador, como se indica en la figura XV.II.

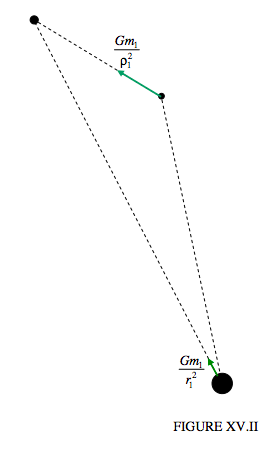
Los componentes x de estos son\( \frac{G m_{1}}{\rho_{1}^{2}} \times \frac{x_{1}-x}{\rho_{1}}\) y\( \frac{G m_{1}}{r_{1}^{2}} \times \frac{x_{1}}{r_{1}}\), y así la aceleración adicional de A, en relación con el Sol, en la dirección X es\( G m_{1}\left(\frac{x_{1}-x}{\rho_{1}^{3}}-\frac{x_{1}}{r_{1}^{3}}\right)\), y esto tiene que agregarse ahora al lado derecho de la Ecuación 15.3.2:

\[ \ddot{x}=-\frac{G(M+m)}{r^{3}} x+G m_{1}\left(\frac{x_{1}-x}{\rho_{1}^{3}}-\frac{x_{1}}{r_{1}^{3}}\right)\]

Ni G ni M son conocidos con gran precisión, pero el producto GM es conocido por una precisión muy grande. Efectivamente en la práctica computacional hacemos uso de la constante gaussiana\( k=\sqrt{\frac{G M}{a_{0}}}\), donde un ₀ es la unidad astronómica de longitud. Esta constante tiene dimensión T ⁻¹ y es igual a la velocidad angular de una partícula de masa despreciable en órbita circular de radio 1 au alrededor del Sol, que es 0.017 202 098 95 radianes por día solar medio. Por lo tanto, en la práctica computacional, la Ecuación 15.3.5 se escribe generalmente como

\[ \ddot{x}=-\frac{k^{2}(1+m)}{r^{3}} x+k^{2} m_{1}\left(\frac{x_{1}-x}{\rho_{1}^{3}}-\frac{x_{1}}{r_{1}^{3}}\right),\]

en el que las unidades de masa, longitud y tiempo son, respectivamente, masa solar, unidad astronómica y día solar medio. Recordemos que m es la masa del asteroide cuya órbita estamos calculando, y m ₁ es la masa del planeta perturbador, y que el origen de las coordenadas es el centro del Sol. Ecuaciones similares se aplican a los componentes y - y z:

\[ \ddot{y}=-\frac{k^{2}(1+m)}{r^{3}} y+k^{2} m_{1}\left(\frac{y_{1}-y}{\rho_{1}^{3}}-\frac{y_{1}}{r_{1}^{3}}\right)\]

\[\ddot{z}=-\frac{k^{2}(1+m)}{r^{3}} z+k^{2} m_{1}\left(\frac{z_{1}-z}{\rho_{1}^{3}}-\frac{z_{1}}{r_{1}^{3}}\right)\]

Si agregamos las perturbaciones de todos los planetas principales desde Mercurio (M) hasta Neptuno (N), estas Ecuaciones se convierten, por supuesto,

\[ \ddot{x}=-\frac{k^{2}(1+m)}{r^{3}} x+k^{2} \sum_{i=M}^{N} m_{i}\left(\frac{x_{i}-x}{\rho_{i}^{3}}-\frac{x_{i}}{r_{i}^{3}}\right)\]

y ecuaciones similares en y y z.

En el caso de un asteroide o un cometa, puede ser permisible descuidar m en esta Ecuación (es decir, establecer m = 0), pero no, por supuesto, m ₁. Vamos a hacer eso aquí, así la Ecuación del movimiento en x se convierte

\[\ddot{x}=-k^{2} \frac{x}{r^{3}}+k^{2} \sum_{i=\mathrm{M}}^{\mathrm{N}} m_{i}\left(\frac{x_{i}-x}{\rho_{i}^{3}}-\frac{x_{i}}{r_{i}^{3}}\right),\]

con ecuaciones similares en y y z.

Los x, x _i, ρ _i, r _i, etc., son datos numéricos, los cuales tienen que ser suministrados por cálculos independientes (subrutinas) para todos los planetas. Como se indicó al final de la Sección anterior, suponemos que tenemos subrutinas en nuestro programa a las que podemos recurrir para calcular estos datos en cualquier fecha. También señalamos que las Ecuaciones de movimiento son válidas para coordenadas eclípticas o ecuatoriales, aunque es más probable que las coordenadas de los planetas estén disponibles es ecuatorial que para coordenadas eclípticas. Todas son funciones del tiempo, de manera que, en efecto, tenemos que desarrollar métodos numéricos para integrar Ecuaciones de la forma, donde f (t) no es una expresión algebraica, sino más bien una tabla de valores numéricos.

\[\ddot{x}=f(t)\]

Es decir

\[\frac{d \dot{x}}{d t}=f(t).\]

Suponemos que conocemos x& en la época de la osculación. Entonces podemos encontrar\(\dot{x}\) en cualquier fecha posterior por cualquier técnica estándar de integración numérica, como las Reglas de Simpson o de Weddle, o la cuadratura gaussiana, o por un proceso Runge-Kutta. Así tenemos ahora una tabla de\(\dot{x}\) como función del tiempo:

\[\dot{x}=g(t)\]

Es decir

\[\frac{d x}{d t}=g(t)\]

Nos integramos por segunda vez, hasta llegar tanto a x como\(\dot{x}\) a alguna época posterior de osculación (quizás 200, o 40, días en el futuro). Repita con los componentes y y z, así que eventualmente tenemos un nuevo conjunto de\((x, y, z, \dot{x}, \dot{y}, \dot{z})\) para una época posterior, y por lo tanto también de a, e, i, Ω, ω, T.