16.1: Introducción

Vamos a considerar el siguiente problema. Dos masas,\(M_1\) y\(M_2\) giran alrededor de su centro de masa mutuo\(\text{C}\) en órbitas circulares, a una distancia constante de\(a\) separación.

\(\text{FIGURE IV.4}\)

El periodo orbital viene dado por

\[P^2 = \frac{4π^2 a^3}{G (M_1 + M_2)} \label{16.1.1} \tag{16.1.1}\]

y la velocidad orbital angular viene dada por

\[ω^2 = \frac{G(M_1 M_2)}{a^3} . \label{16.1.2} \tag{16.1.2}\]

Yo establezco la siguiente notación.

Relación de masa:\[ \frac{M_1}{M_2} = q . \label{16.1.3} \tag{16.1.3}\]

Fracción de masa:\[\frac{M_1}{M_1 + M_2} = µ . \label{16.1.4} \tag{16.1.4}\]

Están relacionados por\[q = \frac{µ}{1 - µ} \label{16.1.5} \tag{16.1.5}\]

y\[µ = \frac{q}{1 + q} . \label{16.1.6} \tag{16.1.6}\]

Observamos las siguientes distancias:

\[\text{M}_1 \text{C} = (1 - µ) a , \quad \text{M}_2 \text{C} = µ a . \label{16.1.7} \tag{16.1.7}\]

Nos hacemos la siguiente pregunta: ¿Hay algún punto en la línea que pasa por las dos masas donde un tercer cuerpo de masa insignificante pueda orbitar alrededor\(\text{C}\) con el mismo periodo que las otras dos masas; es decir, permanecería en la línea que une las dos masas principales?

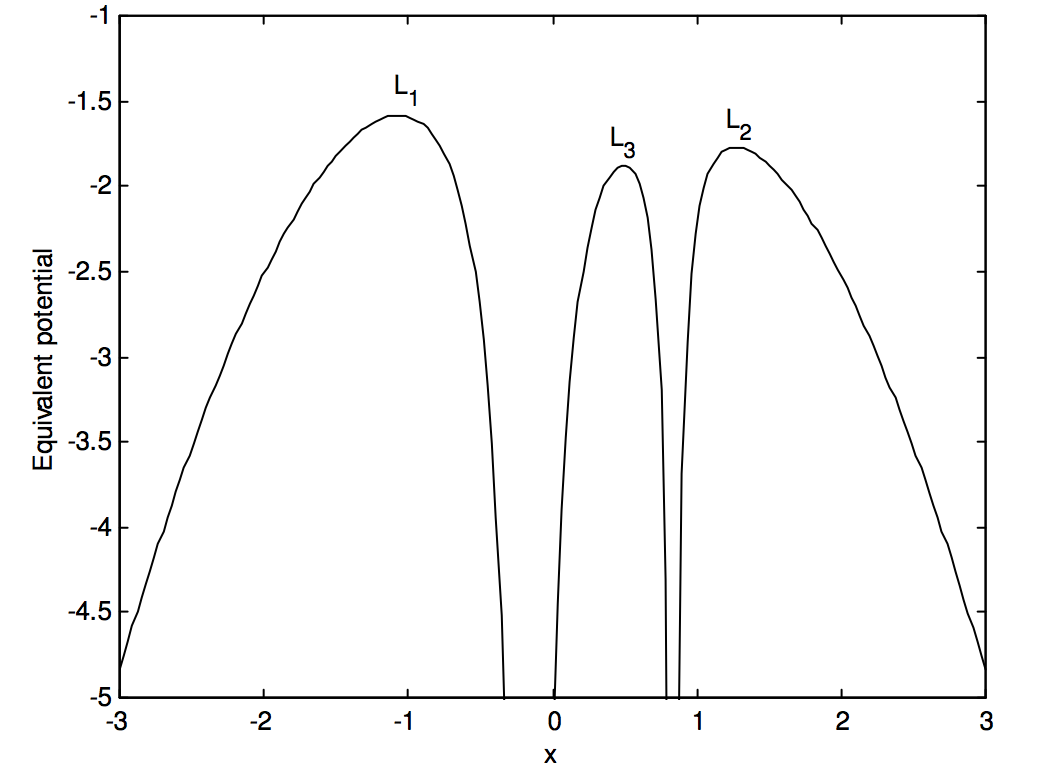
De hecho hay tres puntos de este tipo, y se les conoce como los puntos lagrangianos colineales. (Los puntos colineales fueron discutidos por Euler antes de Lagrange, pero Lagrange llevó el problema más allá y descubrió dos puntos adicionales no colineales con las masas, y los cinco puntos hoy en día son generalmente todos conocidos como los puntos lagrangianos. Discutiremos los puntos adicionales en la Sección 16.2.) He marcado los tres puntos en figura\(\text{XVI.4}\) con las letras\(\text{L}_1\),\(\text{L}_2\) y\(\text{L}_3\).

Nomenclatura

Evidentemente hay\(3! = 6\) formas en las que podría elegir los subíndices. A menudo hoy en día, el punto lagrangiano interno está etiquetado\(\text{L}_1\) y los puntos externos están etiquetados\(\text{L}_2\) y\(\text{L}_3\). Esto me parece carecer de lógica, y elijo etiquetar el punto interior\(\text{L}_3\), y los puntos externos asociados con\(M_1\) y\(M_2\) son entonces\(\text{L}_1\) y\(\text{L}_2\) respectivamente. Por cierto, no estoy haciendo ninguna suposición sobre cuál de los dos cuerpos principales es el más masivo.

Tratemos primero con\(\text{L}_1\). Supongamos que la distancia de\(\text{C}\) a\(\text{L}_1\) es\(xa\).

Una partícula de masa\(m\) en\(\text{L}_1\) está sujeta (en un marco de referencia co-giratorio) a tres fuerzas, a saber, las atracciones gravitacionales de los dos cuerpos principales, y la fuerza centrífuga que actúa lejos de\(\text{C}\). Si este cuerpo va a estar en equilibrio, debemos tener

\[\frac{GM_1 m}{[(x - 1 + µ)a]^2} + \frac{GM_2 m}{[(x + µ) a]^2} = mxa ω^2 . \label{16.1.8} \tag{16.1.8}\]

Al hacer uso de las Ecuaciones 16.1.2 y 16.1.4, encontramos que esta Ecuación se convierte en

\[\frac{µ}{(x -1 + µ)^2} + \frac{1- µ}{(x + µ)^2} = x . \label{16.1.9} \tag{16.1.9}\]

Después de la manipulación, esto se convierte

\[a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + x^5 = 0 , \label{16.1.10} \tag{16.1.10}\]

donde\[a_0 = -1 + 3 µ - 3µ^2 , \label{16.1.11} \tag{16.1.11}\]

\[a_1 = 2 - 4 µ + µ^2 - 2 µ^3 + µ^4 , \label{16.1.12} \tag{16.1.12}\]

\[a_2 = -1 + 2µ - 6µ^2 + 4µ^3 , \label{16.1.13} \tag{16.1.13}\]

\[a_3 = 1 - 6µ + 6µ^2 \label{16.1.14} \tag{16.1.14}\]

y\[a_4 = -2 + 4µ . \label{16.1.15} \tag{16.1.15} \]

Aunque la Ecuación\ ref {16.1.10} es una Ecuación quintica, solo tiene una raíz real para positivo\(µ\).

Las posiciones de\(\text{L}_2\) y se\(\text{L}_3\) pueden encontrar por argumentos exactamente similares —solo hay que tener cuidado con las direcciones y distancias de las dos fuerzas gravitacionales.

Para\(\text{L}_2\), los coeficientes son los mismos que para\(\text{L}_1\), excepto

\[a_1 = -2 + 4µ + µ^2 - 2µ^3 + µ^4 , \label{16.1.16} \tag{16.1.6}\]

\[a_2 = -1 - 2µ + 6µ^2 - 4µ^3 \label{16.1.17} \tag{16.1.17}\]

y\[a_4 = 2 - 4 µ . \label{16.1.18} \tag{16.1.18}\]

Para\(\text{L}_3\) los coeficientes son

\[\begin{align} a_0 &= 1 - 3µ + 3µ^2 - 2µ^3 , \label{16.1.19} \\[5pt] a_1 &= 2 - 4µ + 5µ^2 - 2µ^3 + µ^4 , \label{16.1.20} \\[5pt] a_2 &= 1 - 4µ + 6µ^2 - 4µ^3 , \label{16.1.21} \\[5pt] a_3 &= 1 - 6µ + 6µ^2 \label{16.1.22} \\[5pt] a_4 &= 2 - 4µ . \label{16.1.23} \end{align}\]

(Recordatorio: Al calcular alguno de estos polinomios, escríbelos en términos de paréntesis anidados. Véase Capítulo 1, Sección 1.5.)

También es de interés ver el potencial equivalente (gravitacional más centrífugo). La expresión de energía potencial gravitacional es, como de costumbre\(−GMm/r\), dónde\(r\) está la distancia a la masa\(M\). La expresión de la energía potencial centrífuga es\(-\frac{1}{2} m ω^2 r^2\), donde\(r\) está la distancia desde el centro de masa. Lo negativo de la derivada de esta expresión es\(mω^2 r\) que es la expresión habitual para la fuerza centrífuga. Cuando aplicamos estos principios al sistema de dos masas bajo consideración, obtenemos la siguiente expresión para el potencial equivalente (que, en esta sección, sólo voy a llamar en\(V\) lugar de\(V^\prime\)).

\[V = - \frac{GM_1}{|x + 1 - µ| a} - \frac{GM_2}{|x - µ| a} - \frac{1}{2}x^2 a^2 ω^2 . \label{16.1.24} \tag{16.1.24}\]

Al hacer uso de las Ecuaciones\ ref {16.1.2} y\ ref {16.1.4}, encontramos que esta Ecuación se convierte

\[W = - \frac{µ}{|x + 1 - µ|} - \frac{1 - µ}{|x - µ|} - \frac{x^2}{2}, \label{16.1.25} \tag{16.1.25}\]

donde\[W = V \div \left( \frac{G(M_1 + M_2)}{a} \right) . \label{16.1.26} \tag{16.1.26}\]

Establecer las derivadas de esta expresión a cero da, por supuesto, las posiciones de los puntos lagrangianos, pues estos son puntos de equilibrio donde la derivada del potencial es cero. La figura\(\text{XVI.5}\) muestra el potencial para una relación de masa\(q = 5\). Obsérvese que, en la línea que une las dos masas, el potencial equivalente en los puntos lagrangianos es máximo, y por lo tanto estos puntos, mientras que los puntos de equilibrio, son inestables. Veremos en la Sección 16.6 que los puntos son en realidad puntos de silla de montar. Si bien varias naves espaciales están en órbita o se planea que estén en órbita alrededor de los puntos lagrangianos colineales (por ejemplo,\(\text{SOHO}\) en el punto lagrangiano interior, y\(\text{MAP}\) en\(\text{L}_2\)), presumiblemente se necesita un pequeño gasto continuo de combustible para mantenerlos allí.

Será de interés ver cómo varían las posiciones de los puntos lagrangianos con la fracción de masa. De hecho, la masa se puede transferir de un miembro de un sistema estelar binario al otro durante la evolución de un sistema estelar binario. Discutiremos un poco más adelante cómo puede suceder esto. Por el momento, sin preocuparnos por el mecanismo exacto, solo variaremos la fracción de masa y veremos cómo varían las posiciones de los puntos lagrangianos a medida que lo hacemos. Sin embargo, si la masa se transfiere de un miembro de un sistema binario de estrellas al otro,

\(\text{FIGURE XVI.5}\)

y si no hay pares externos en el sistema, se conservará el momento angular\(L\) del sistema y, para asegurar esto, la separación\(a\) de las dos estrellas cambia con la fracción de masa.

Ejemplo\(\PageIndex{1}\)

Demostrar que, para un momento angular orbital dado\(L\) del sistema, la separación\(a\) de los componentes varía con la fracción másica según

\[a = \frac{L^2}{GM^3 µ^2 (1-µ)^2}. \label{16.1.27} \tag{16.1.27}\]

Solución

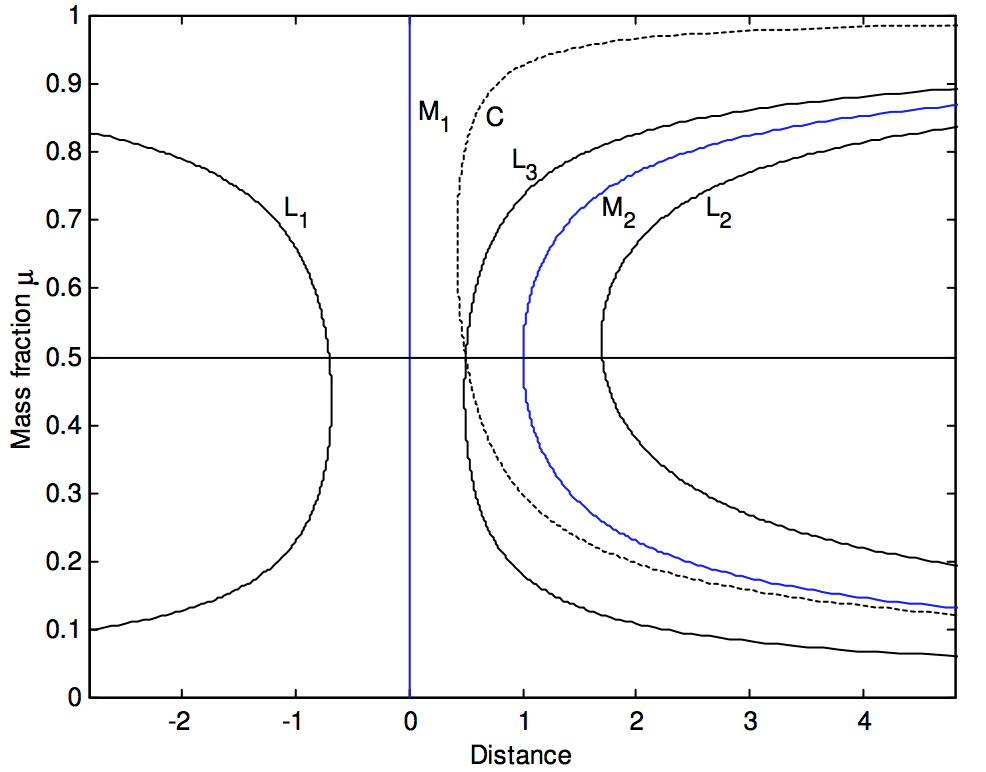
Aquí\(M = M_1 + M_2\) está la masa total del sistema. En la figura\(\text{XVI.6}\) he utilizado esta Ecuación, más las Ecuaciones\ ref {16.1.10} y\ ref {16.1.7}, para calcular las distancias de\(\text{M}_2\),\(\text{C}\), y los tres puntos lagrangianos de\(\text{M}_1\) como una función de la fracción de masa. La unidad de distancia en la figura\(\text{XVI.6}\) es\(16 L^2 /(GM^3)\), que es la separación de las dos masas cuando las dos masas son iguales. Cada una de estas distancias tiene un valor mínimo para una fracción de masa particular. Estas distancias mínimas, y las fracciones másicas para las que ocurren, son las siguientes:

\ begin {array} {c c c}
&\ text {Valor mínimo} &\ text {Fracción de masa}
\\\ texto {M} _1\ texto {C} & 0.421875^* & 0.66666\ punto {6}\
\ texto {M} _1\ texto {L} _2 & 1.690392 & 0.524579\
\ texto {M} _1\ texto {M} _2 y 1.1.000000 y 0.500000\\
\ text {M} _1\ texto {L} _3 & 0.489038 & 0.446273\\
\ texto {M} _1\ texto {L} _1 & 0.677756 & 0.436062\\
\ end {array}

\(^* 0.421875 = 27/64 \ \text{exactly}\)

\(\text{FIGURE XVI.6}\)

¿Cómo puede ocurrir realmente la transferencia de masa en un sistema estelar binario? Bueno, las estrellas no son puntos —son cuerpos esféricos grandes. Cuando el hidrógeno se agota en el núcleo por reacciones termonucleares, una estrella se expande enormemente (“deja la secuencia principal”) y cuando se expande tanto que las capas externas de su atmósfera alcanzan el punto lagrangiano interno, la materia de la estrella grande se derrama hacia la otra estrella. La más masiva de las dos estrellas en un sistema binario generalmente evoluciona más rápido; es la primera en abandonar la secuencia principal y expandirse para que su atmósfera llegue a los puntos lagrangianos internos. Uno puede imaginar a la estrella más masiva llenando gradualmente su potencial pozo de figura\(\text{XVI.5}\), hasta que se desborda y gotea sobre la colina potencial del punto interior, para luego caer en el pozo potencial de su compañero.

Una forma de interpretar la figura\(\text{XVI.6}\) es imaginar que\(\text{M}_1\) comienza con una gran fracción de masa cercana a 1, y por lo tanto cerca de la parte superior de la figura\(\text{XVI.6}\). Ahora imagina que esta estrella pierde masa ante su compañera, de manera que la fracción de masa disminuye. Empezamos a movernos por la\(\text{M}_1\) línea de la figura\(\text{XVI.6}\). Vemos el punto interior\(\text{L}_3\) acercándose cada vez más. Si la superficie de la estrella se encuentra\(\text{L}_3\) mientras aún\(\text{L}_3\) se acerca (es decir, si la fracción de masa es aún mayor que 0.446273), entonces una mayor transferencia de masa hará que el\(\text{L}_3\) acercamiento sea cada vez más rápido y, por lo tanto, la transferencia de masa será rápida. Cuando la fracción de masa es inferior a 0.5, la estrella que originalmente era la estrella más masiva es ahora menos masiva que su compañera. Cuando la fracción de masa se haya reducido por debajo de 0.446273, la transferencia de masa adicional se\(\text{L}_3\) alejará y, por lo tanto, la transferencia de masa adicional será lenta.

En los cálculos de Ejemplo\(\PageIndex{1}\), asumí que las estrellas pueden ser tratadas gravitacionalmente como si fueran fuentes puntuales —y así pueden ser, por grandes que sean, siempre y cuando sean esféricamente simétricas. Al inicio de la transferencia de masa, la estrella que pierde masa está bastante distorsionada y está lejos de ser esférica. Sin embargo, esta distorsión afecta principalmente a la atmósfera exterior de la estrella y, siempre que el mayor volumen de la estrella esté contenido dentro de un volumen aproximadamente esféricamente simétrico, la aproximación de la fuente puntual debería seguir siendo buena. La otra suposición que hice fue que se conserva el momento angular orbital. Hay dos razones por las que esto podría no ser así —pero para ambos es probable que haya muy poca pérdida de momento angular orbital. Una posibilidad es que la masa pueda perderse del sistema, a través de uno u otro o ambos puntos lagrangianos colineales externos. Sin embargo, la figura\(\text{XVI.5}\) muestra que los potenciales de estos puntos son apreciablemente mayores que el punto interno; por lo tanto, la transferencia de masa se realiza mucho antes de la pérdida de masa. Otra razón por la que el momento angular orbital podría conservarse es la siguiente. Cuando la materia de la estrella que pierde masa se transfiere a través del punto interior a la estrella que gana masa, o fluye sobre la colina potencial interior, no se mueve en línea recta directamente hacia la segunda estrella. Todo este análisis se ha referido a un marco de referencia corrotativo, y cuando la materia se mueve de\(\text{M}_1\) hacia\(\text{M}_2\), está sujeta a una fuerza de Coriolis (ver sección 4.9 de Mecánica Clásica), que la envía alrededor\(\text{M}_2\) en un disco de acreción. Durante este proceso se conserva el momento angular total del sistema (siempre que no se pierda masa del sistema) pero esto ahora debe ser compartido entre el momento angular orbital de las dos estrellas y el momento angular del disco de acreción. Sin embargo, mientras este último sea una contribución relativamente pequeña al momento angular total, la conservación del momento angular orbital sigue siendo una aproximación realista.